数字信号处理:傅里叶分析
本文主要参考视频如下:
数字信号处理9-1_线性时不变系统对复指数信号的响应_哔哩哔哩_bilibili
傅里叶分析的主要研究内容如下所示:
注意,计算机中使用的离散傅里叶变换并不是离散时间傅里叶变换;
前四种都是理论上的变换方式,最后一种是计算机应用中的变换方式。
连续时间周期信号的傅里叶级数
要注意,连续时间周期信号的傅里叶级数是一个离散的结果,是一系列谐波的离散组合。
理论上,任何一个周期信号都可以进行傅里叶级数的分解,但是不一定能收敛,所以一般只有满足狄利赫里条件的周期信号才能展开成傅里叶级数。
满足狄利赫里条件时,在不连续的点处会出现吉布斯现象
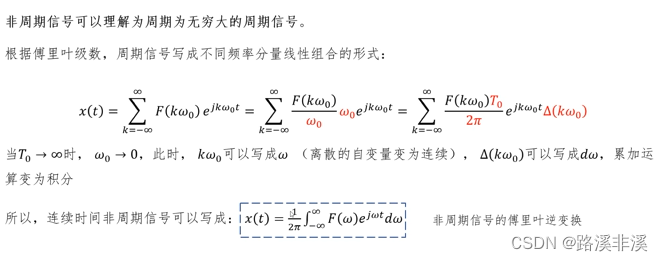
连续时间非周期信号的傅里叶变换
注意,连续时间非周期信号的傅里叶变换是一个频率密度的概念,是一个连续的函数,以w为自变量
频谱越来越密。
逆变换到时域
周期信号的傅里叶级数也可以统一到傅里叶变换
注意,傅里叶级数的结果是频谱,傅里叶变换的结果是频谱密度。
连续时间傅里叶变换的性质
1、共轭和共轭对称性
2
3
4
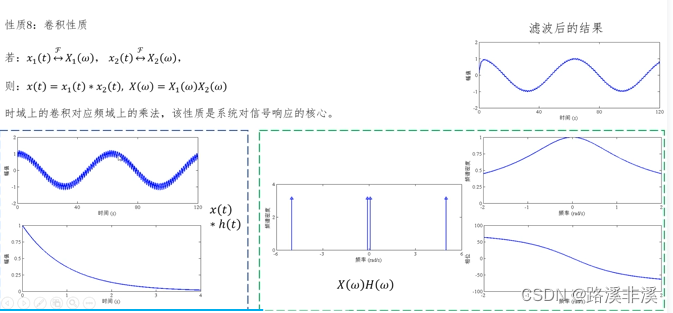
如果时域卷积不方便计算,可以转换成对应频率的相乘。
5
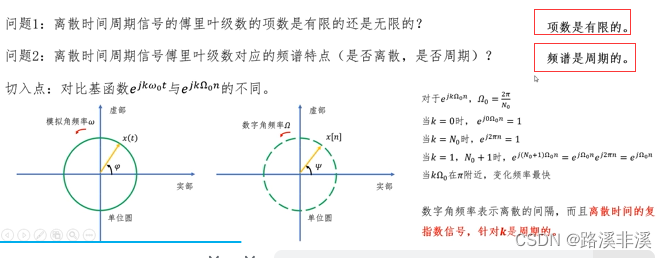
离散时间周期信号的傅里叶级数
注意下,连续时间周期信号的傅里叶级数是一个无穷级数;
离散时间周期信号的傅里叶级数只需要在一个周期上展开即可;
举个例子
离散时间周期信号的频谱是周期延拓的
存在性
可见,任何离散时间周期信号的傅里叶级数必定存在,不需要满足什么额外条件;
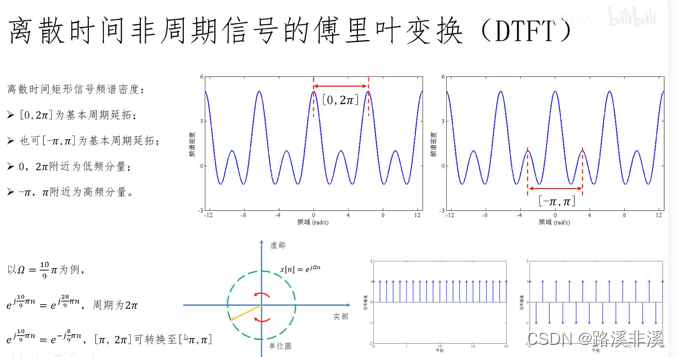
离散时间非周期信号的傅里叶变换
逆变换
存在性
频谱密度图像是以2π为周期进行周期沿拓的
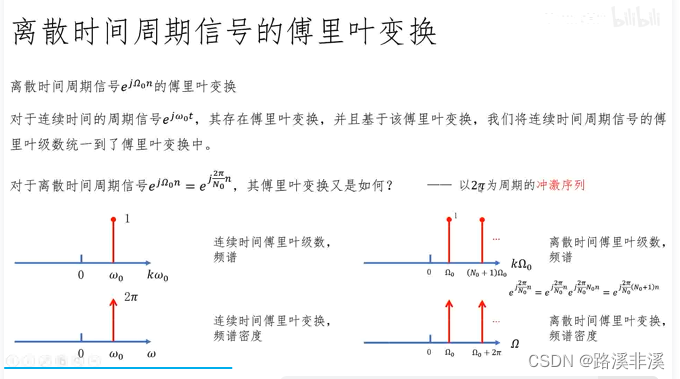
离散时间周期信号也可以统一到傅里叶变换
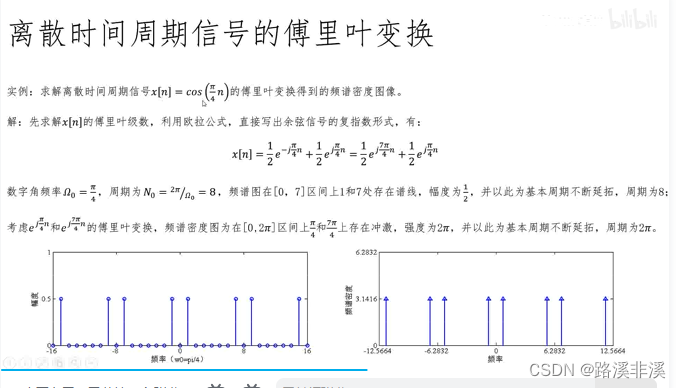
举个例子
离散时间傅里叶变换的性质
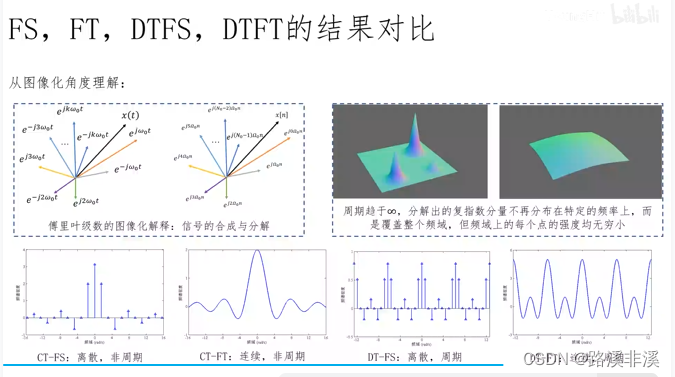
以上几种傅里叶变换的对比
图像化理解
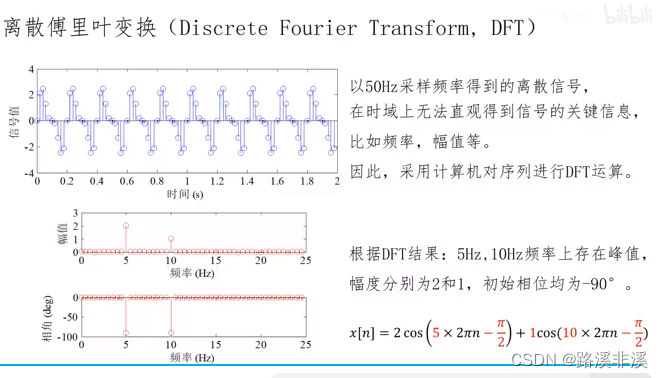
离散傅里叶变换DFT
离散傅里叶变换是基于离散时间周期信号的傅里叶级数的,是计算机处理信号的方式。
它是暴力地将离散信号的长度N0就看做周期为N0的离散时间周期信号,然后计算其DFS,但是相比DFS会少一个系数,需要我们手动处理,这就是DFT
这种简单粗暴的方式是否合理呢?给一颗定心丸,肯定是合理的。
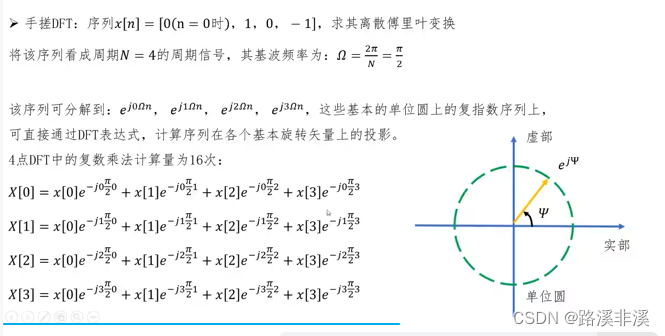
举个例子
再举个实际的例子
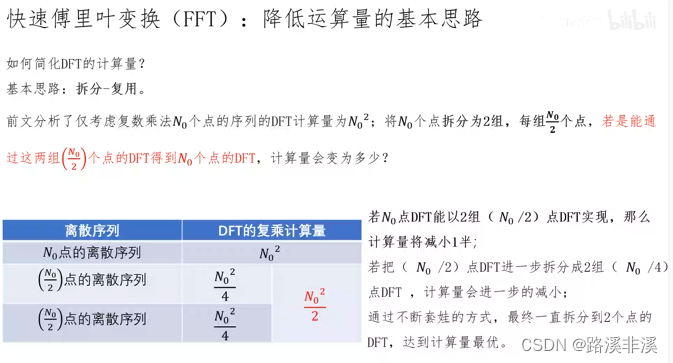
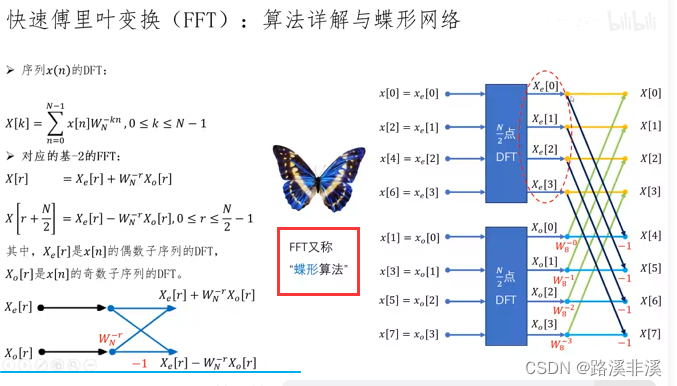
快速傅里叶变换FFT
FFT其实就是DFT的快速算法
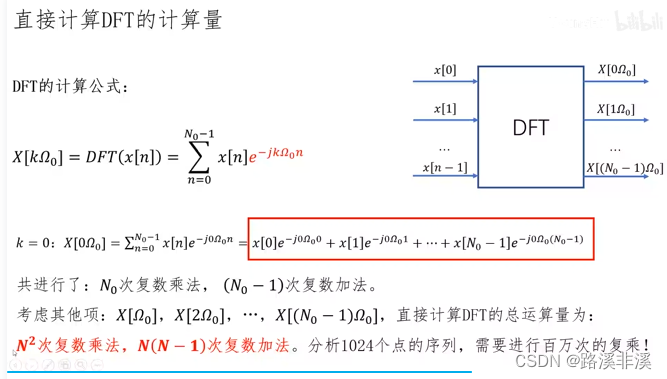
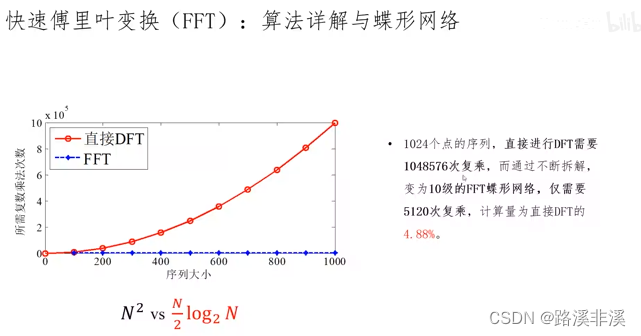
DFT的计算量
具体实现过程可参考这个视频
数字信号处理13-2_快速傅里叶变换(FFT)-降低运算量的基本思路_哔哩哔哩_bilibili
不在此赘述了
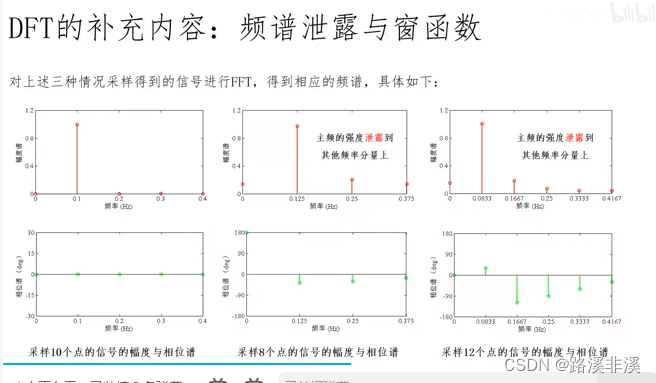
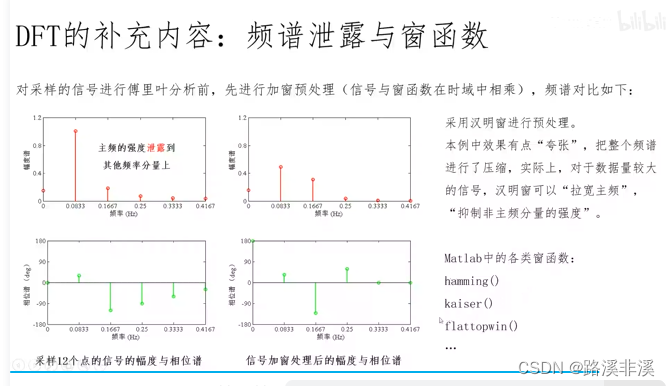
频谱泄漏和窗函数
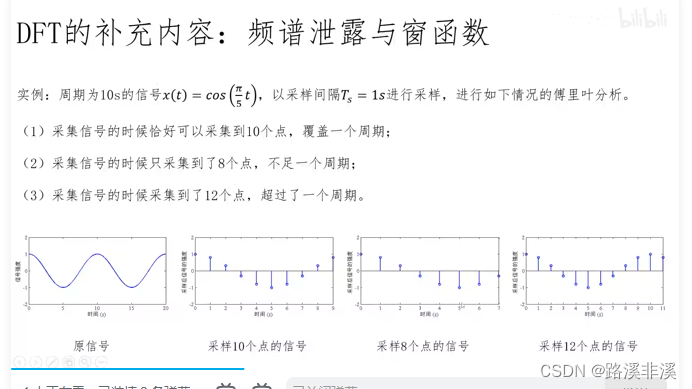
举个实例来说明什么是频谱泄漏
假如刚好采集到一个周期,那么就能反应真实情况
但是如果信号本身就没有周期呢?或者采集的不到一个周期或者超过一个周期呢?就有误差了。
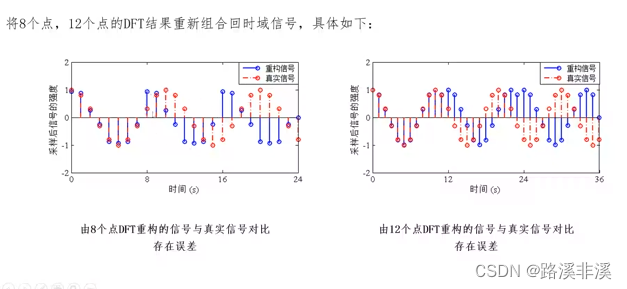
还原回去看下
如何减弱频谱泄漏的影响
实际中,窗函数一般不这么用,在滤波器设计中用得比较多。
相关文章:
数字信号处理:傅里叶分析
本文主要参考视频如下: 数字信号处理9-1_线性时不变系统对复指数信号的响应_哔哩哔哩_bilibili 傅里叶分析的主要研究内容如下所示: 注意,计算机中使用的离散傅里叶变换并不是离散时间傅里叶变换; 前四种都是理论上的变换方式&…...

pat 甲级 1051 Pop Sequence
思想:如果要弹出一个数,那么说明比它小的数字已经进栈了,所以要在一个数num输入之后把比它小的数都输入到栈中,直到栈满或者valnum时结束入栈操作。如果valnum,将这个值弹出,否则说明整个序列存在问题,把fl…...

Stable Diffusion 绘画入门教程(webui)-ControlNet(深度Depth)
上篇文章介绍了线稿约束,这篇文章介绍下深度Depth 文章目录 一、选大模型二、写提示词三、基础参数设置四、启用ControlNet 顾名思义,就是把原图预处理为深度图,而深度图可以区分出图像中各元素的远近关系,那么啥事深度图…...
Rust-知多少?
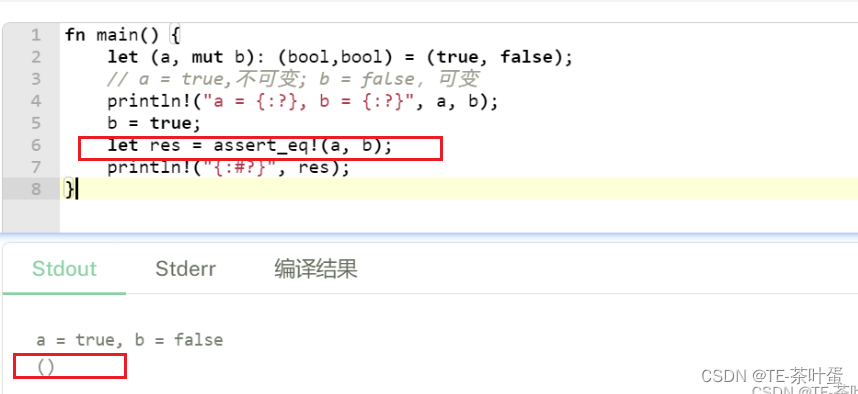
文章目录 前言1.使用下划线开头忽略未使用的变量2. 变量解构3.常量4.变量遮蔽(shadowing)5. 类似println!("{}", x); 为啥加感叹号6.单元类型7. -> 运算符到哪去了?总结 前言 Rust 学习系列,记录一些rust使用小技巧…...

Qt不规则可移动窗体的实现
实现: 可以借助不规则的位图来实现不规则窗体,并支持拖动和移动。下面分别是头文件和源文件 #ifndef SHAPEWIDGET_H #define SHAPEWIDGET_H#include <QWidget>class ShapeWidget : public QWidget {Q_OBJECTpublic:ShapeWidget(QWidget *parent …...
Jakarta Bean Validation
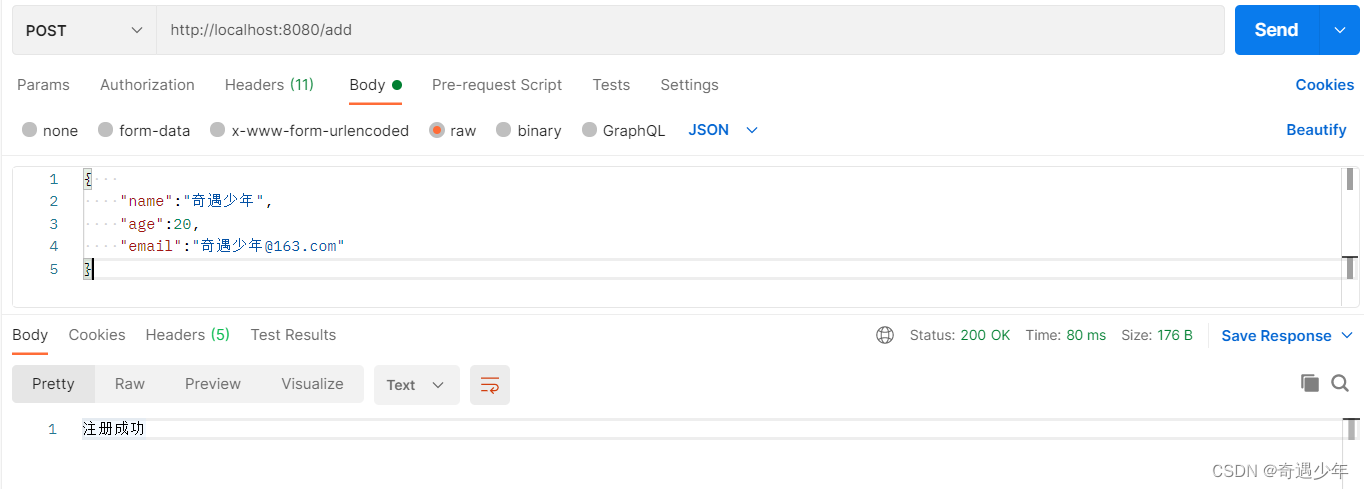
Validation 官网 https://beanvalidation.org/ 常见注解 Bean Validation中定义的注解: 注解详细信息Null被注释的元素必须为 nullNotNull被注释的元素必须不为 nullAssertTrue被注释的元素必须为 trueAssertFalse被注释的元素必须为 falseMin(value)被注释的元素…...
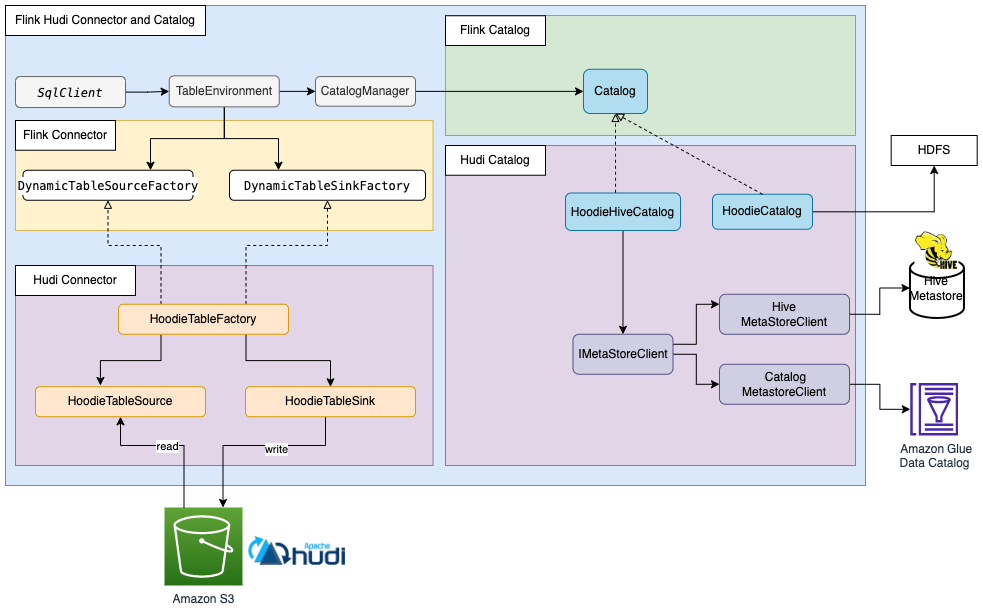
Flink Catalog 解读与同步 Hudi 表元数据的最佳实践
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...
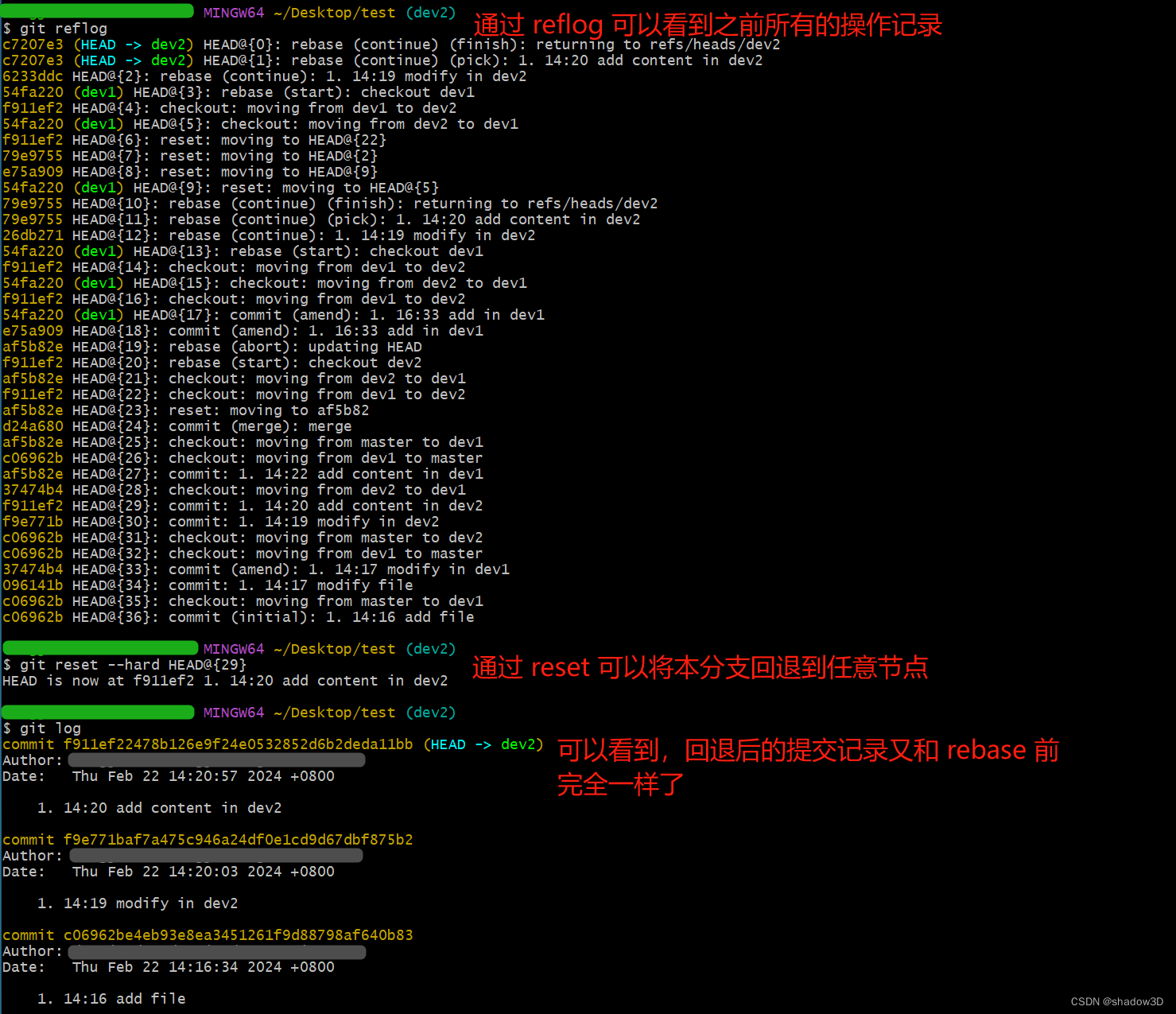
git 使用总结
文章目录 git merge 和 git rebasegit mergegit rebase总结 git merge 和 git rebase git merge git merge 最终效果说明: 假设有一个仓库情况如下,现需要进行 merge: merge 操作流程: merge 的回退操作: git reba…...

【Elasticsearch专栏 01】深入探索:Elasticsearch的正向索引和倒排索引是什么
文章目录 什么是Elasticsearch的正向索引和倒排索引?1.倒排索引(Inverted Index)2.正向索引(Forward Index)3.小结 什么是Elasticsearch的正向索引和倒排索引? 首先,要明确的是,Ela…...

Linux、Ubuntu、CenterOS、RedHat、Debian、AIpine关系和区别?
目录 1. 区别和联系 2. 安装命令 3. 其他发行版本 4. 拓展知识 Linux 内核和操作系统发行版的关系-CSDN博客 5.参考 1. 区别和联系 Ubuntu, Debian, RedHat, CentOS都是不同的Linux发行版。 Ubuntu 是基于Debian的一个开源GNU/Linux操作系统。它的目标是为一般用户提供…...
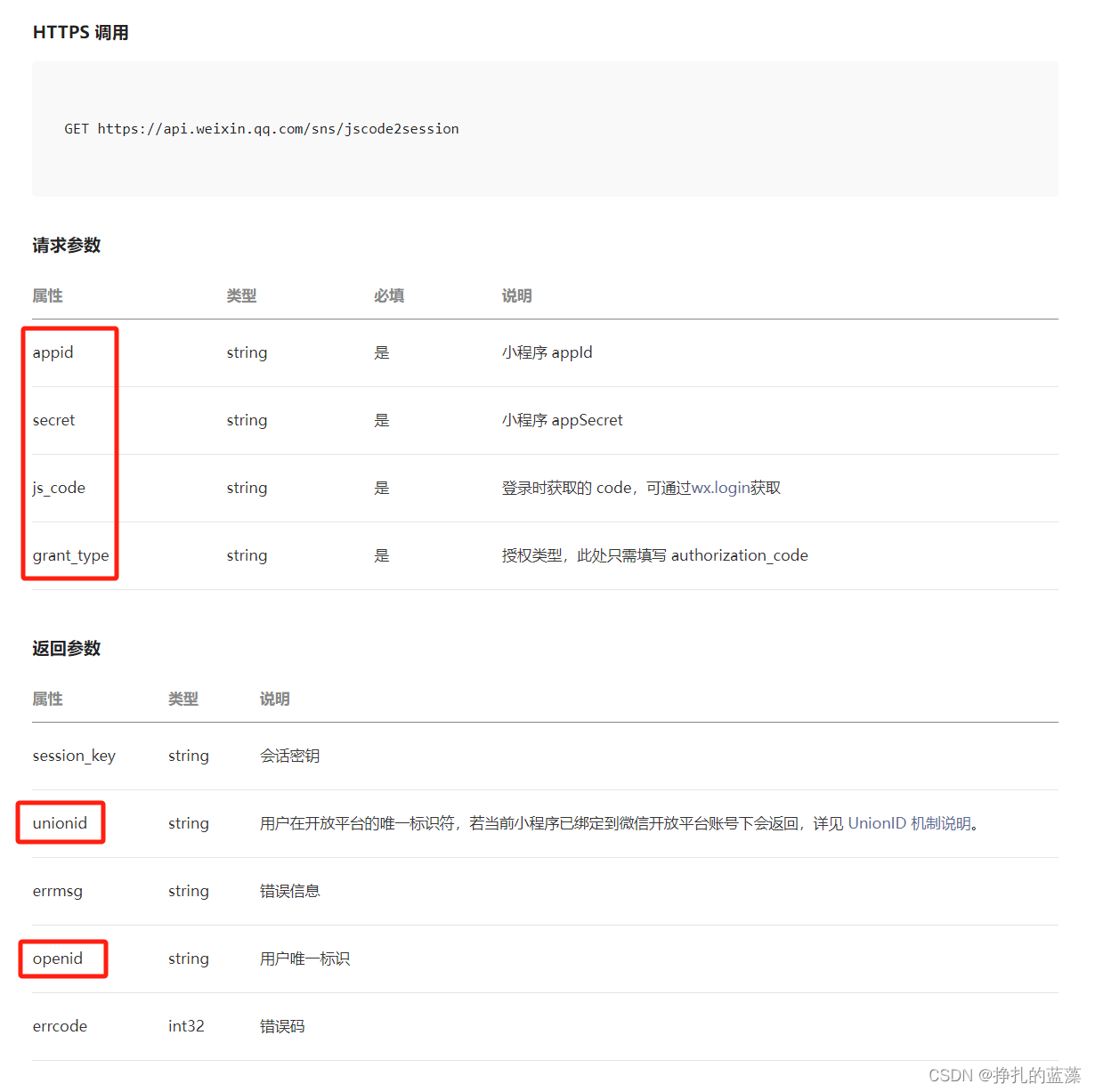
微信小程序开发:通过wx.login()获取用户唯一标识openid和unionid
下面代码展示了 openid 的获取过程。 想获取 unionid 需要满足条件:小程序已绑定到微信开放平台账号下,不然只会返回 openid。 【相关文档】 微信小程序开发:appid 和 secret 的获取方法 wx.login({success (res) {if (res.code) {// 发起网…...
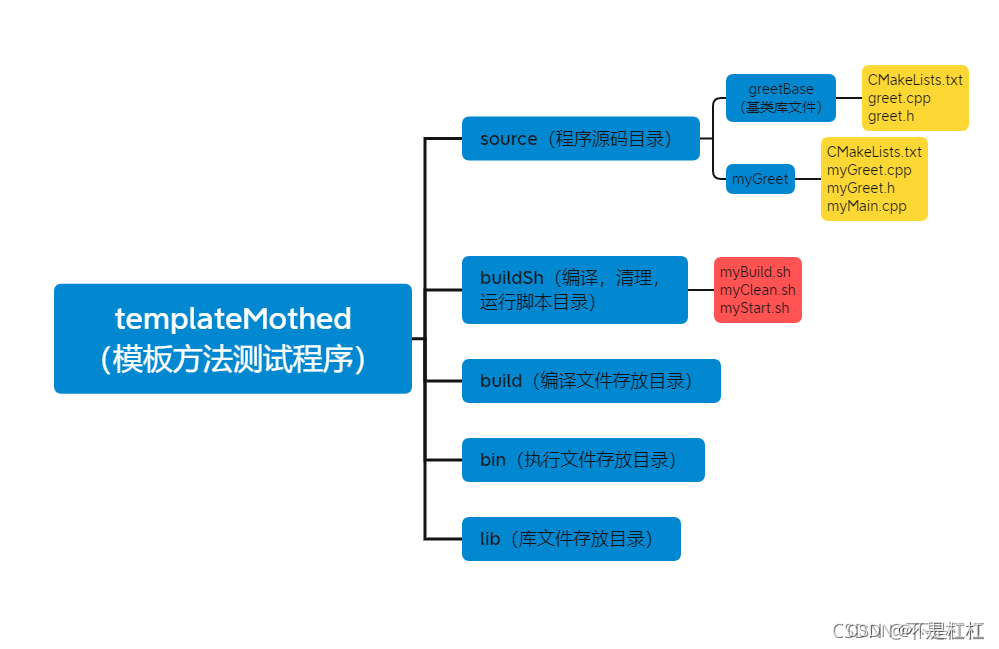
设计模式之模板方法
模式定义 定义一个操作中的算法的骨架 (稳定),而将一些步骤延迟(变化)到子类中。Template Method使得子类可以不改变(复用)一个算法的结构即可重定义(override 重写)该算法的某些特定步骤。 …...
Tubi 故事|中国团队本地管理队伍的形成
当一支团队在公司核心业务中发挥着越来越重要的作用,他们将会获得更多资源以支持团队的发展并在核心业务中持续贡献。相应地,公司也需要投入更多的精力去管理这支规模日渐壮大的团队,尤其当这支远程团队与公司总部在地理和文化上有明显差异时…...
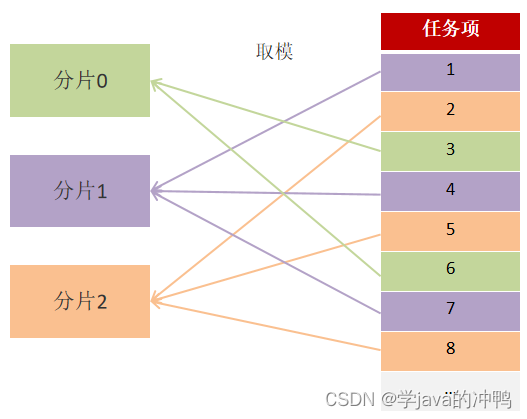
微服务篇之任务调度
一、xxl-job的作用 1. 解决集群任务的重复执行问题。 2. cron表达式定义灵活。 3. 定时任务失败了,重试和统计。 4. 任务量大,分片执行。 二、xxl-job路由策略 1. FIRST(第一个):固定选择第一个机器。 2. LAST&#x…...
提取游戏音频文件.bnk
提取游戏音频文件.bnk 什么是.bnk准备Wwise-Unpacker工具使用Wwise-Unpacker工具总结 什么是.bnk .bnk其实是一种对音频的加密方式,一个.bnk文件中通常包含了多个语音文件,一般可以使用Wwise-Unpacker来解码.bnk格式文件 准备Wwise-Unpacker工具 Wwis…...

React 模态框的设计(三)拖动组件的完善
我在上次的Draggable组件的设计中给了一个简化的方法,今天我来完善一下这个组件,可用于任何可移动组件的包裹。完善后的效果如下所示: 这个优化中,增加了一个注目的效果,还增加了触发可拖动区域的指定功能,…...
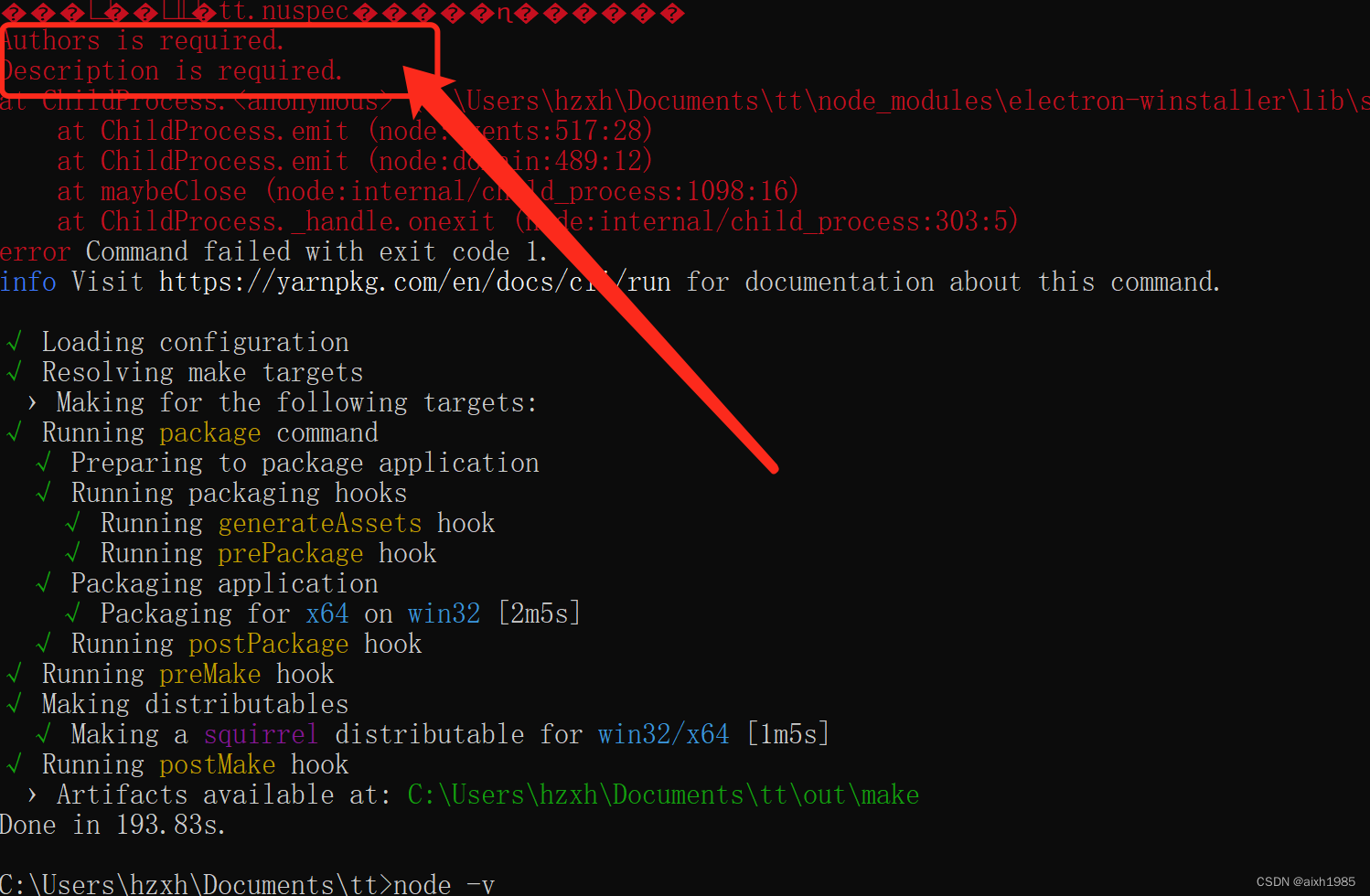
wondows10用Electron打包threejs的项目记录
背景 电脑是用的mac,安装了parallels desktop ,想用electron 想同时打包出 苹果版本和windows版本。因为是在虚拟机里安装,它常被我重装,所以记录一下打包的整个过程。另外就是node生态太活跃,几个依赖没记录具体版本࿰…...

git的master、develop、feature分支分别是做什么用的?有什么区别和联系?
在Git版本控制系统中,master、develop和feature分支都是常用的分支类型,它们有不同的用途和特点。 master分支:master分支是Git默认的主分支,它包含了项目的稳定版本。通常,master分支用于发布正式版本,即经…...

前端基础面试题
摘要:最近,看了下慕课2周刷完n道面试题,记录下... 1.请说明Ajax、Fetch、Axios三者的区别 三者都用于网络请求,但维度不同: Ajax(Asynchronous Javascript ang XML),是一种在不重新…...
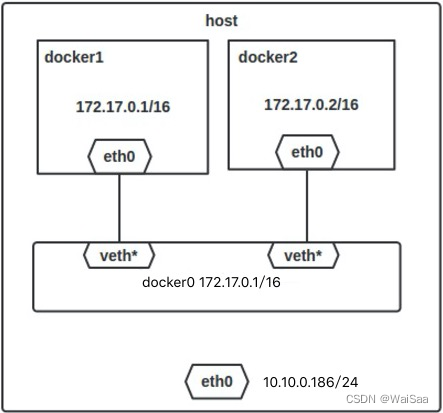
docker自定义网络实现容器之间的通信
Background docker原理 docker是一个Client-Server结构的系统,Docker的守护进程运行在主机上。通过Socket从客户端访问。docker核心三大组件:image–镜像、container-容器、 repository-仓库。docker使用的cpu、内存以及系统内核等资源都是直接使用宿主…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...