考研第一天,汤家凤基础班,连续与极限复习笔记
函数连续极限
- 性质
- 保号性
- 证明极值点:
- 夹逼准则
- 二项式展开
- 根号下,大于一,小于一的讨论
- 直接放缩求和
- 分子分母齐次,且分母大一次,用积分
- 单调有界存在极限
- 几个重要的切线放缩
- 证明有界,然后放缩求单调
- 证明有界,然后相减求单调
- 无穷小
- 性质记忆
- 重要极限
- 重大考点不定型
- 零分之零
- 基本解法
- 注意无穷小的介
- 加减转化注意精确度
- 正常敏感变化:
- 注意ln()变化出一
- 对tan的不爽
- 分子有理化
- 一分之无穷
- 基本解法
- 例题
- 无穷分之无穷
- 基本解法
- 例题
- 零乘以无穷
- 转化为零比零 或者无穷比无穷就行
- 无穷减无穷
- 获得分母是求解的关键
- 提取公因试获得分母
- 分子有理化获得分母(注意技巧忽略小项)
- 通分获得分母
- 无穷分之零,零分之无穷
- 解题方法
- 例题
- 连续
- 间断点
- 例题
- 介值定理
- 存在函数区间,和函数求和,证明值存在
性质
保号性
证明极值点:
- 通过保号性,证明该点与附件的大小:
*
- 通过保号性确定附件导数的正负号:

夹逼准则
- 分子分母有一个不齐的时候用

二项式展开

根号下,大于一,小于一的讨论

直接放缩求和

分子分母齐次,且分母大一次,用积分
- 例题一,例题二:

单调有界存在极限
几个重要的切线放缩

证明有界,然后放缩求单调
- 例题一:

- 例题二:

证明有界,然后相减求单调

无穷小
性质记忆

重要极限

重大考点不定型

零分之零
基本解法
- 函数的指数函数 求e分之ln
- ln(…)------------>ln(1+…)~…
- (…)-1------------->
- e^a-1------------->a
- (1+a)^b---------------->ba
注意无穷小的介
- 这几个相减全为三阶
- 一个重要的 x减ln(x+1)

加减转化注意精确度

正常敏感变化:

注意ln()变化出一

对tan的不爽

分子有理化

一分之无穷
基本解法
- 转化为(1+0)^∞
- 恒等变化

例题

无穷分之无穷
基本解法
- 看增长速度 ,对数小于幂函数小于指数函数
- 看最高相次数
- (可能要洛必达)

例题
-
二项式定理

-
洛必达

- 除以,得到无穷小

零乘以无穷
转化为零比零 或者无穷比无穷就行
无穷减无穷
获得分母是求解的关键
提取公因试获得分母

分子有理化获得分母(注意技巧忽略小项)

通分获得分母

无穷分之零,零分之无穷
解题方法
- 直接e^ln()
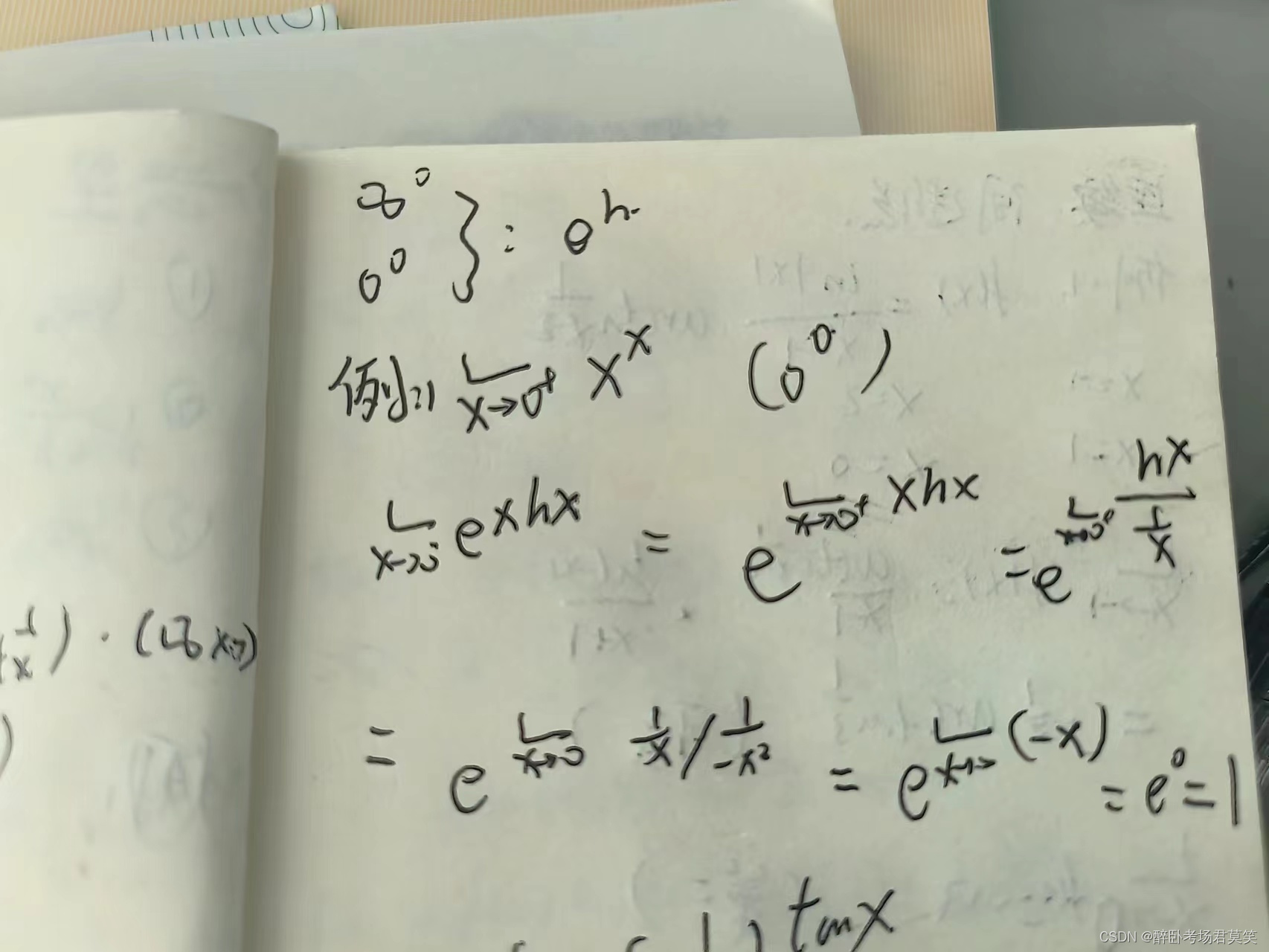
例题
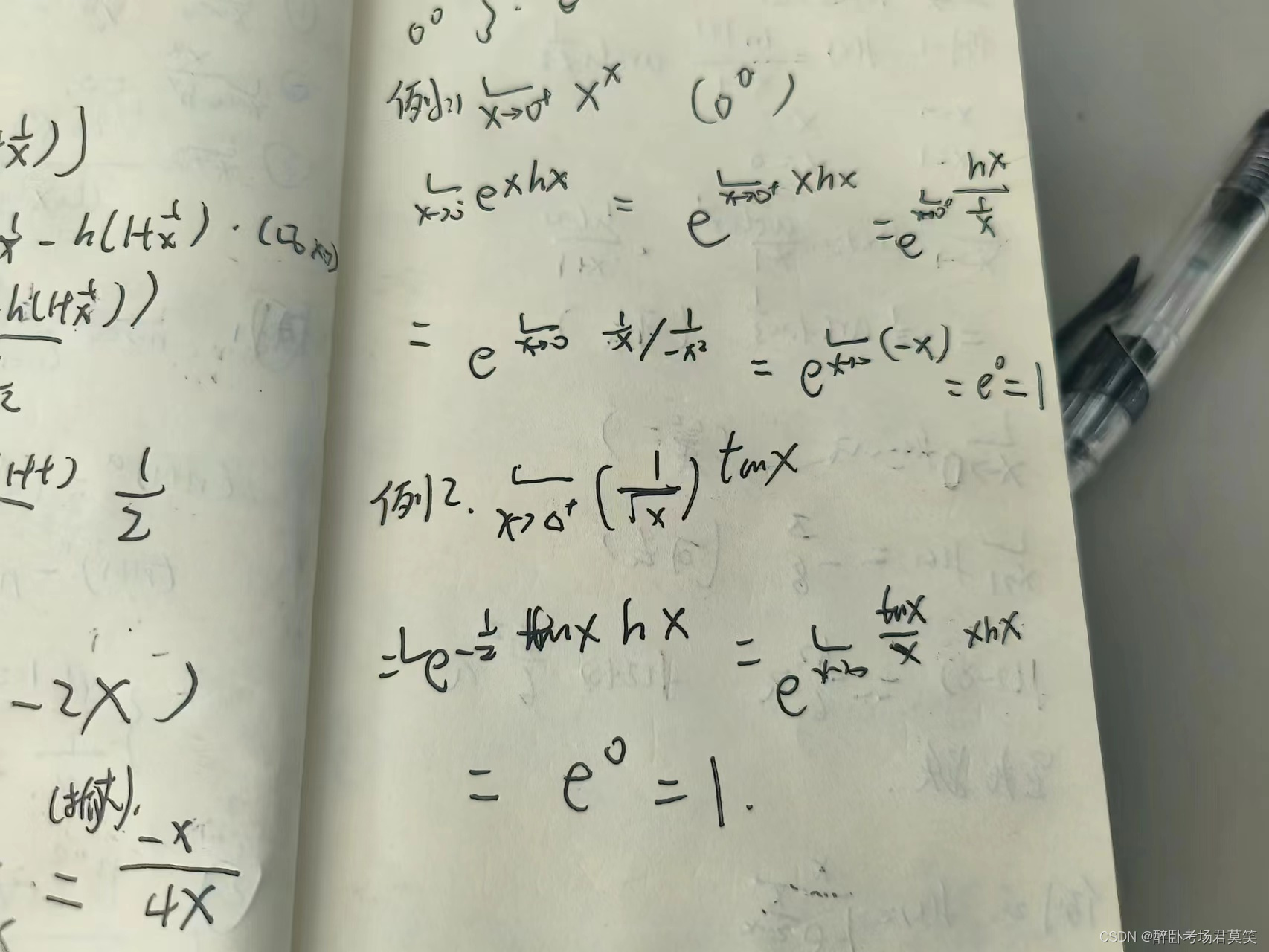
连续
间断点
- 找定义域中的间断点
- 左右极限相等就是可去
- 左右相等不相等就是跳跃
- 有无穷就是第二类

例题


介值定理
存在函数区间,和函数求和,证明值存在

相关文章:

考研第一天,汤家凤基础班,连续与极限复习笔记
函数连续极限性质保号性证明极值点:夹逼准则二项式展开根号下,大于一,小于一的讨论直接放缩求和分子分母齐次,且分母大一次,用积分单调有界存在极限几个重要的切线放缩证明有界,然后放缩求单调证明有界&…...

聊一聊代码重构——关于变量的代码实践
提炼变量 其目标是将一个复杂表达式或语句分解成更小的部分,并将其存储在变量中。提高代码可读性和复用性 复杂的表达式 有些时候为了方便我们会把业务处理的逻辑写在一起,如果参与处理的内容较多时我们就会创造出一个非常长且难以理解的表达式。当其他…...

Spring之基于注解方式实例化BeanDefinition(1)
最近开始读Spring源码,读着读着发现里面还是有很多很好玩的东西在里面的,里面涉及到了大量的设计模式以及各种PostProcessor注入的过程,很好玩,也很复杂,本文就是记录一下我学习过程中的主干流程。 在开始我们源码解读…...

【STM32】入门(十四):FreeRTOS-任务
1、简述 FreeRTOS应用程序由一组独立的任务构成。 在任何时间点,应用程序中只能执行一个任务,FreeRTOS调度器负责决定所要执行的任务。 每个任务在自己的上下文中执行,不依赖于系统内的其他任务或 FreeRTOS的调度器本身。 FreeRTOS调度器负责…...

apscheduler 的基本介绍和使用
APScheduler有四大组件: 1、触发器 triggers : 触发器包含调度逻辑。每个作业都有自己的触发器,用于确定下一个任务何时运行。除了初始配置之外,触发器是完全无状态的。 有三种内建的trigger: (1)date: 特定…...

Oracle中merge Into的用法
Oracle中merge Into的用法 使用场景 在操作数据库时,数据存在的情况下,进行update操作;不存在的情况下,进行insert操作;在Oracle数据库中,能够使用merge into来实现。 基本语法 merge into table_name …...
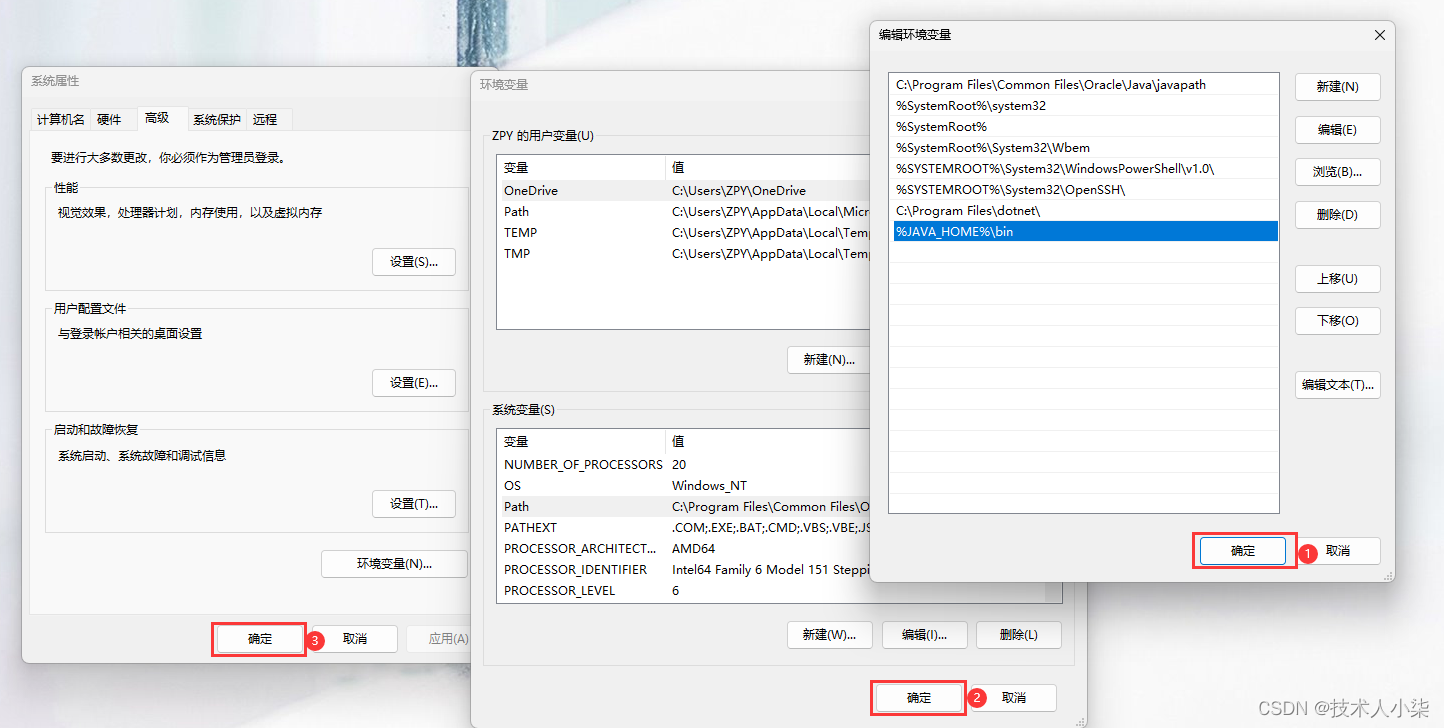
JDK19下载、安装与测试的完整图文教程
一、下载JDK 1、官网获取:https://www.oracle.com/ 1.1 点击“Products”; 1.2 选择“Java”; 1.3 选择“Download Java”; 1.4 选择“Java downloads”,这里以最新版(JDK19)为例ÿ…...
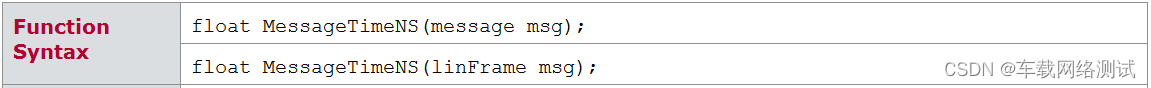
Vector - CAPL - 获取相对时间函数
在自动化开发中,无论是CAN通信测试,还是网络管理测试,亦或是休眠唤醒等等存在时间相关的,都可能会使用相关的时间函数;今天主要介绍的就是获取当前时间,我们知道vector工具的最大优势就是稳定和精确度高&am…...

C++编程语言STL之unordered_map介绍
本文主要介绍 C 编程语言的 STL(Standard Template Library) 中 unordered_map 的相关知识,同时通过示例代码介绍 unordered_map 的常见用法。1 概述C标准库提供了四个无序关联容器(unordered associated container)&a…...
)
【独家】华为OD机试 - 最快检测效率-核酸(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明本期…...
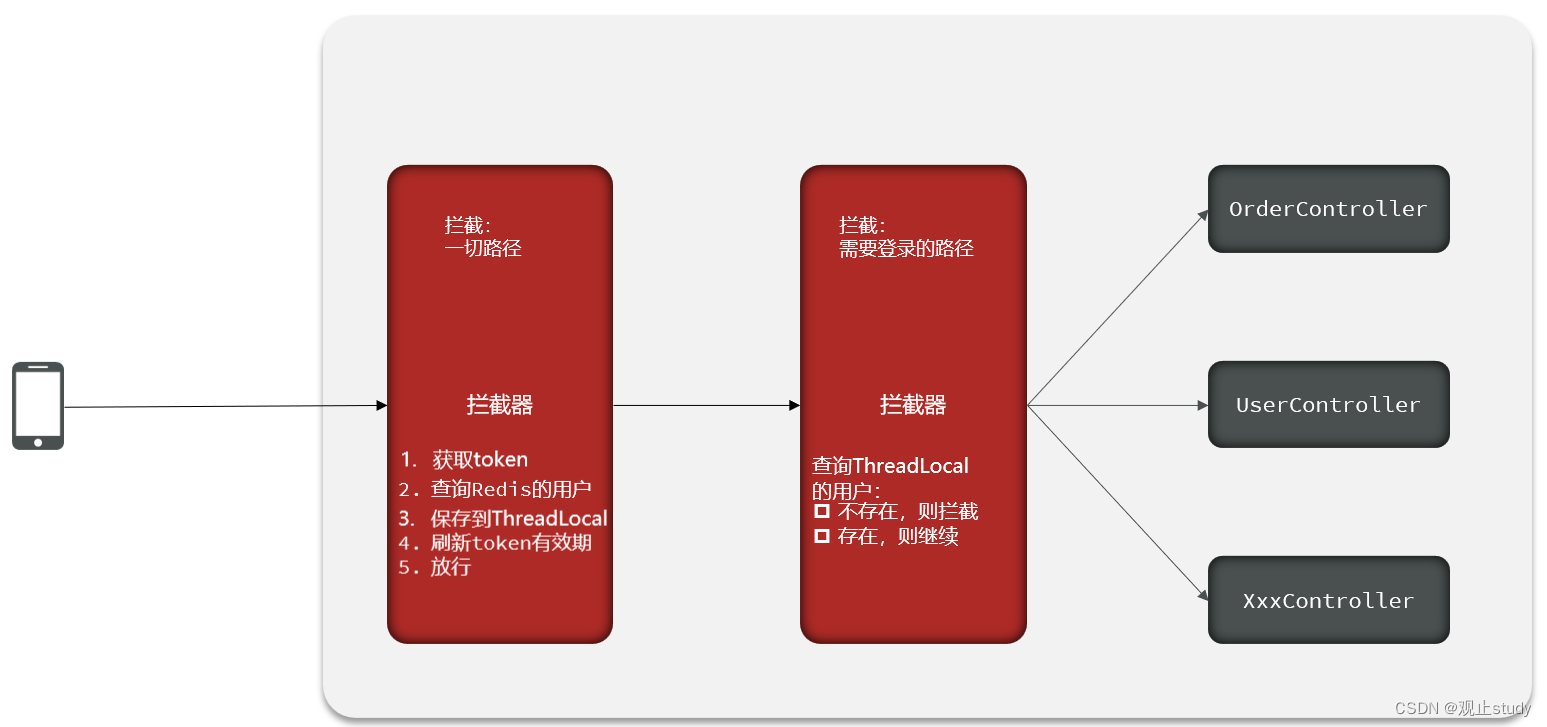
【Redis应用】基于Redis实现共享session登录(一)
🚗Redis应用学习第一站~ 🚩本文已收录至专栏:数据库学习之旅 👍希望您能有所收获 👉相关推荐:使用短信服务发送手机验证码进行安全校验 一.引入 在开发项目过程中,我们常常能碰到需要登录注…...
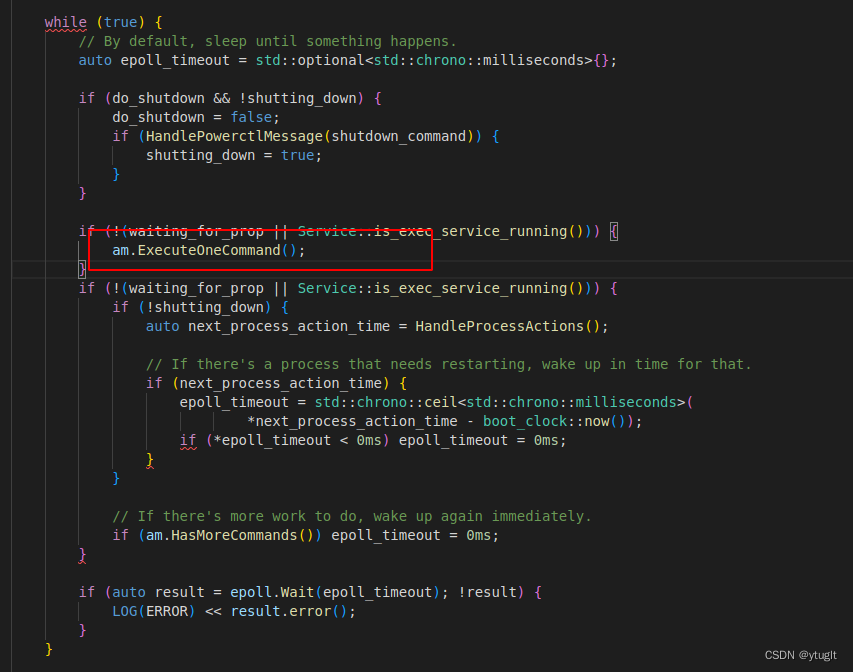
Android framework系列2 - Init进程
1、源码 入口:system/core/init/main.cpp2 流程图 https://note.youdao.com/s/EtnCswft 3、代码详解 主入口共三步,如流程图所示,我们主要看下最后一步 入口在init.cpp下,这个阶段主要来解析init.rc并执行此文件下的命令 看到…...
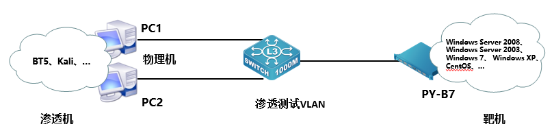
2023年“网络安全”赛项江苏省淮安市选拔赛 任务书
任务书 一、竞赛时间 共计3小时。 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 第一阶段单兵模式系统渗透测试 任务一 服务器内部信息获取 任务二 网站渗透测试 任务三 Linux系统渗透提权 任务四 Web渗透测试 第二阶段分组对抗 备战阶段 攻防对抗准备工作 系统加…...

2023年Wireshark数据包分析——wireshark0051.pcap
Wireshark数据包分析 任务环境说明: 服务器场景:FTPServer220223服务器场景操作系统:未知(关闭连接)FTP用户名:wireshark0051密码:wireshark0051从靶机服务器的FTP上下载wireshark0051.pcap数据包文件,找出黑客获取到的可成功登录目标服务器FTP的账号密码,并将黑客获…...

SpringMVC的自定义配置和自动化配置
SpringBoot的自动配置MVC处理加载逻辑基于Spring Boot的MVC自动化配置由WebMvcAutoConfiguration类完成,部分关键源码:AutoConfiguration(after { DispatcherServletAutoConfiguration.class, TaskExecutionAutoConfiguration.class,ValidationAutoConf…...

画图说透 ZooKeeper如何保证数据一致性:选举和ZAB协议
1、zookeeper是什么? zookeeper能被各个牛逼的中间件项目中所依赖,已经说明了他的地位。一出手就是稳定的杀招。zookeeper是什么?官网中所说,zookeeper致力于开发和维护成为一个高度可靠的分布式协调器。 开局一张图,…...
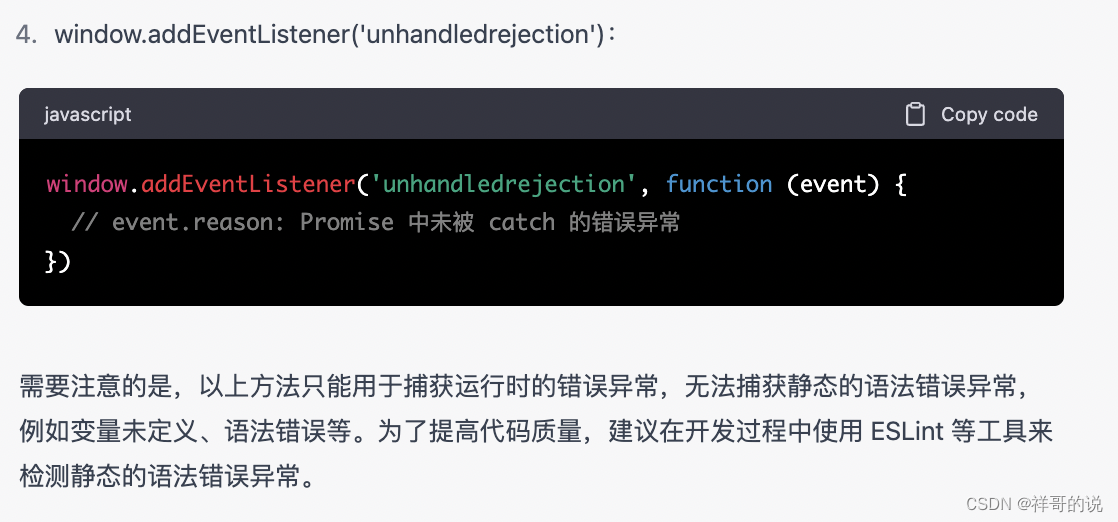
错误异常捕获
1、React中错误异常捕获 在 React 中,可以通过 Error Boundaries(错误边界)来捕获错误异常。Error Boundaries 是一种 React 组件,它可以在其子组件树的渲染期间捕获 JavaScript 异常,并且可以渲染出备用 UI。React 提…...

js垃圾回收机制
内存的生命周期 ]S环境中分配的内存,一般有如下生命周期 1.内存分配:当我们声明变量、函数、对象的时候,系统会自动为他们分配内存 2.内存使用:即读写内存,也就是使用变量、函数等 3.内存回收: 使用完毕,由垃圾回收器自动回收不再…...
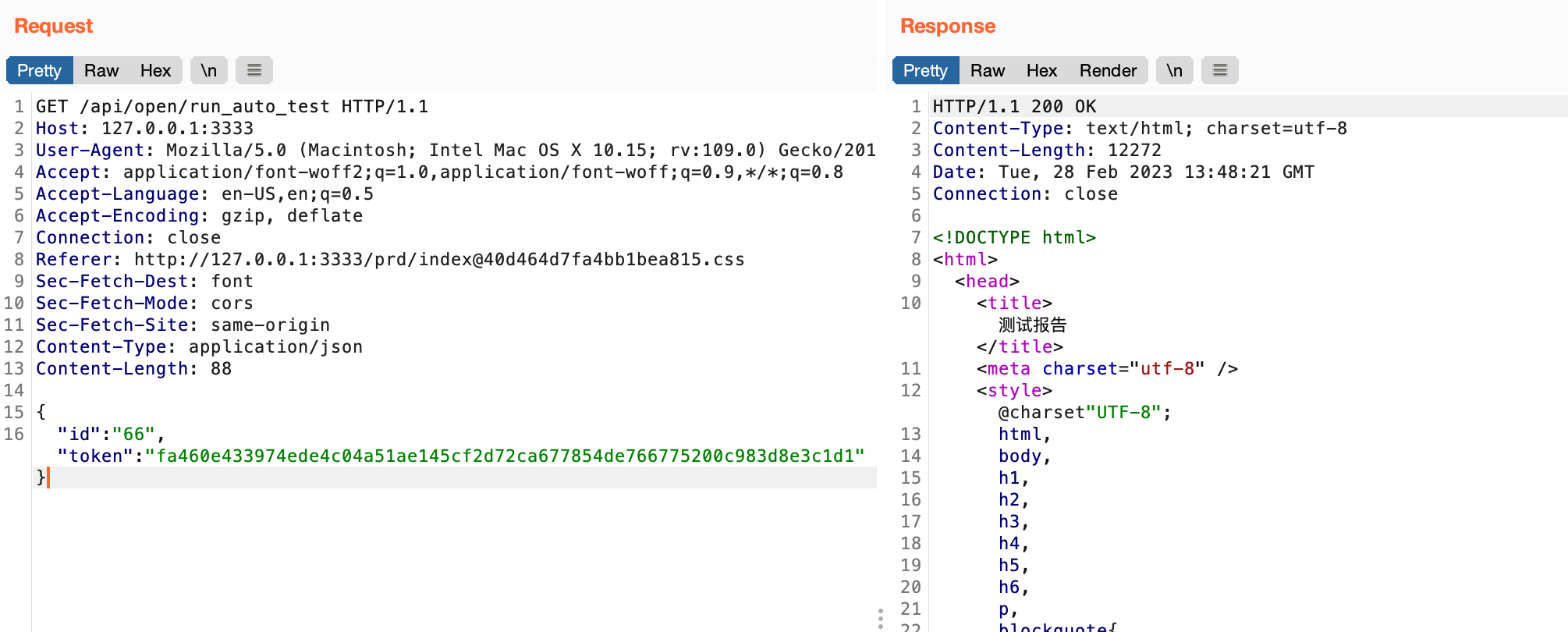
YApi分析从NoSQL注入到RCE远程命令执行.md
0x00 前提 这个是前几个月的漏洞,之前爆出来发现没人分析就看了一下,也写了一片 Nosql注入的文章,最近生病在家,把这个写一半的完善一下发出来吧。 0x01 介绍 YApi是一个可本地部署的、打通前后端及QA的、可视化的接口管理平台…...
【C++】stl_list介绍和实现,list和vector区别,list vector string 迭代器失效
本篇博客详细介绍list的实现&细节讲解,并且在文章末对list和vector,string进行区分和复习 list的基本结构就是双向带头循环链表,链表和顺序表的差别我们在前面数据结构的时候早就学过了,不再赘述 在使用stl库里面list时&…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...


