蓝桥杯DP算法——区间DP(C++)

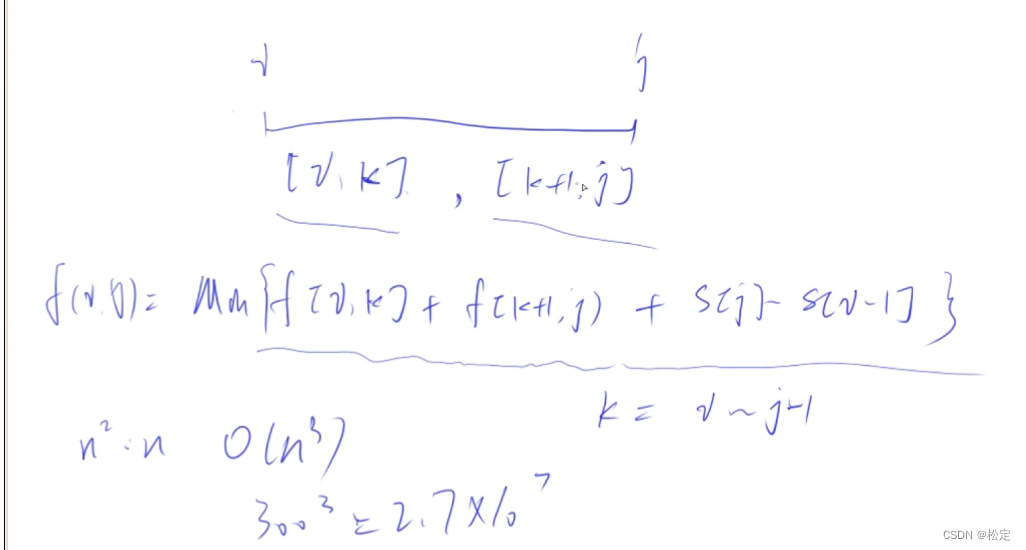
根据题意要求的是将石子合并的最小权值,我们可以根据DP思想使用二维数组f[i,j]来存放所有从第i堆石子到第j堆石子合并成一堆石子的合并方式。
然后由第二个图所示,我们可以将i到j区间分成两个区间,因为将i到j合并成一个区间的前一步一定是合并前两个区间。因此我们可以将状态计算的递归定义为区间的中间,通过变化区间的中间来寻找合并i到j的最小值。
也就是f[i,j]=min(f[i,k]+f[k+1,j]+s[j]-s[i-1]
例题:https://www.acwing.com/problem/content/284/
#include<iostream>
using namespace std;const int N=310;
int n;
int f[N][N];
int s[N];int main()
{cin>>n;int a;for(int i=1;i<=n;i++) //前缀和{scanf("%d",&a);s[i]=s[i-1]+a;}for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){int l=i ,r=i+len-1;f[l][r]=1e8;for(int k=l;k<r;k++){f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);}}}cout<<f[1][n];return 0;
}k的取值范围:
这里划分出的区间是[l, k], [k+1, r]
说明: [l, l] [r, r] 这两个区间都是不为空的,至少包含了一堆石子。
前提:划分出的两个区间都不为空的情况下,讨论k的取值范围
所以,对于[l, k] k可以取到 l 对于[k+1, r] , 因为k+1 <= r, 所以 k <= r - 1, 即 k < r
相关文章:
蓝桥杯DP算法——区间DP(C++)
根据题意要求的是将石子合并的最小权值,我们可以根据DP思想使用二维数组f[i,j]来存放所有从第i堆石子到第j堆石子合并成一堆石子的合并方式。 然后由第二个图所示,我们可以将i到j区间分成两个区间,因为将i到j合并成一个区间的前一步一定是合…...
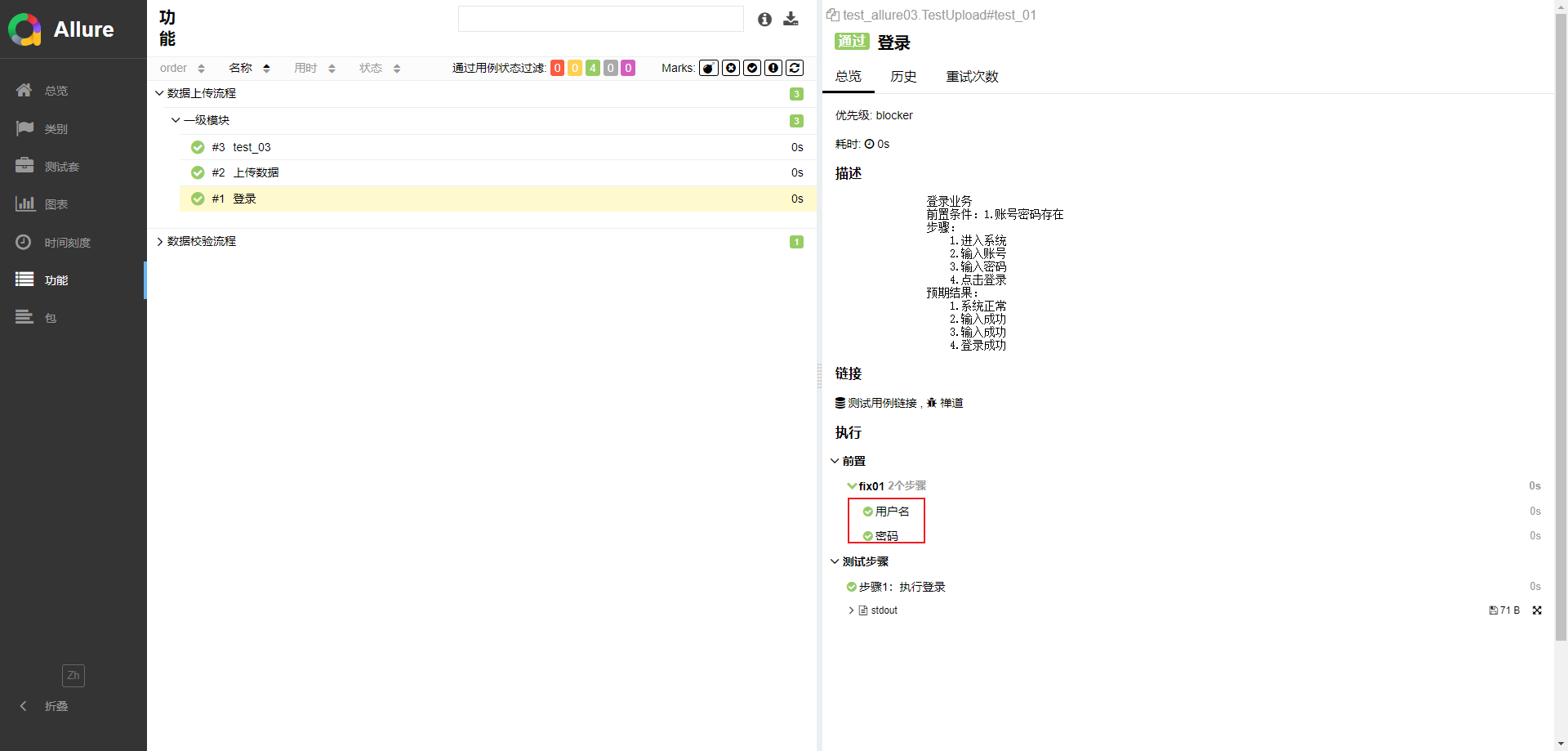
pytest结合Allure生成测试报告
文章目录 1.Allure配置安装2.使用基本命令报告美化1.**前置条件**2.**用例步骤****3.标题和描述****4.用例优先级**3.进阶用法allure+parametrize参数化parametrize+idsparametrize+@allure.title()4.动态化参数5.环境信息**方式一****方式二**6.用例失败截图1.Allure配置安装 …...
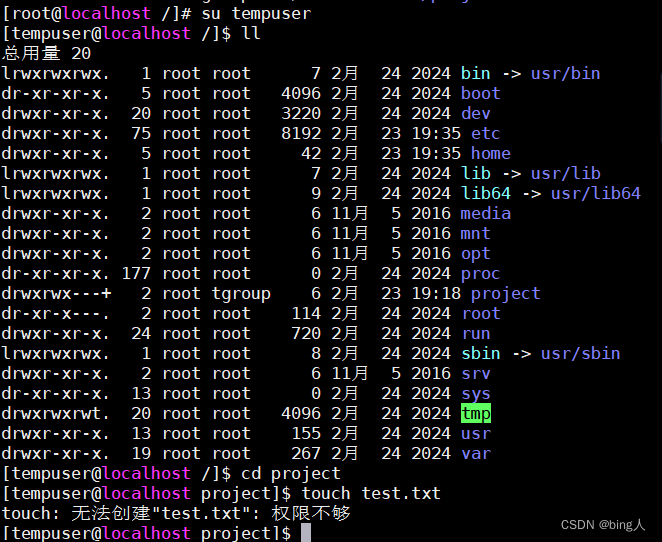
Linux--ACL权限管理
一.ACL权限管理简介 ACL(Access Control List,访问控制列表)是一种文件权限管理机制,它提供了比传统的UGO(用户、组、其他)权限更灵活的权限设置方式。以下是ACL的一些主要功能: 针对特定用户或…...
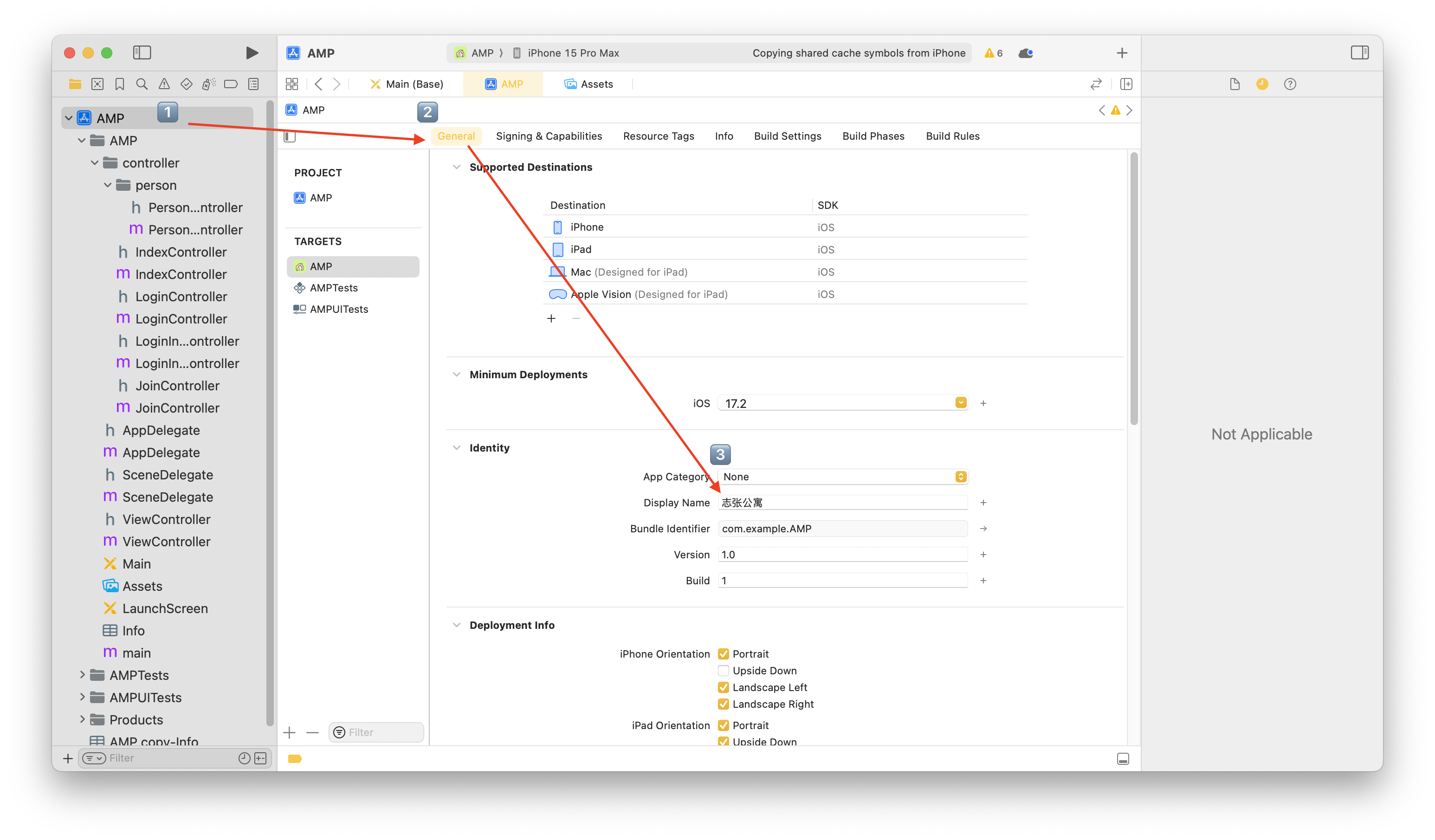
Xcode中App图标和APP名称的修改
修改图标 选择Assets文件 ——> 点击Applcon 换App图标 修改名称 点击项目名 ——> General ——> Display Name...
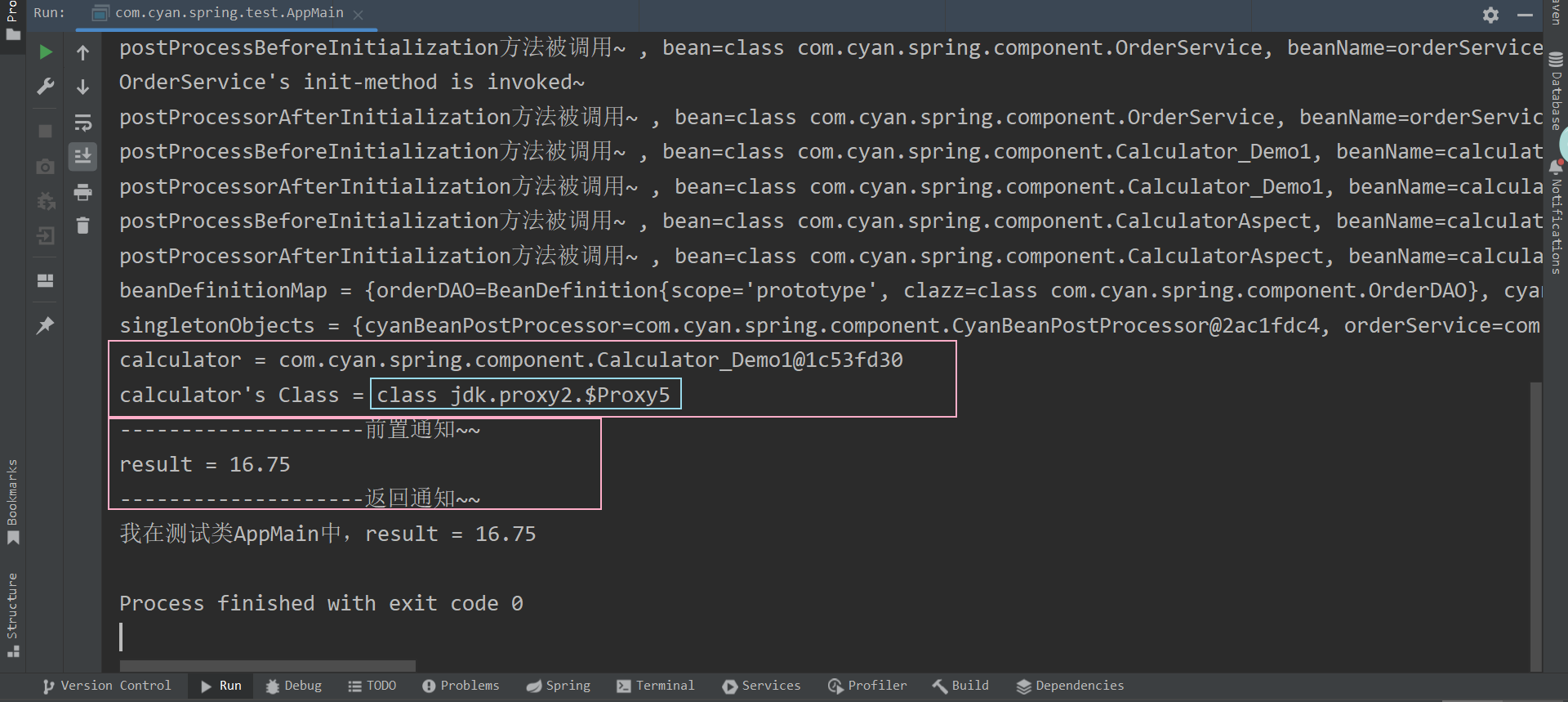
Spring 手动实现Spring底层机制
目录 一、前言 二、Spring底层整体架构 1.准备工作 : 2.架构分析 : (重要) 3.环境搭建 : 三、手动实现Spring容器结构 1.自定义注解 : 1.1 Component注解 1.2 Scope注解 2.自定义组件 : 3.自定义用于封装Bean信息的BeanDefinition类&a…...

CSV数据导入到ClickHouse数据库
问题描述:手头上有一个数据量较大的CSV文件,希望导入到指定的ClickHouse数据中,ClickHouse部署在服务器中。 解决方案:通常来说,数据量较少的CSV文件可以直接通过DBeaver软件的可视化界面导入数据。 若数据量较大&…...

第十二天-ppt的操作
目录 创建ppt文档 安装 使用 段落的使用 段落添加数据 段落中定义多个段落 自定义段落 ppt插入表表格 PPT插入图片 读取ppt 读取ppt整体对象 编辑 获取ppt文本 获取表格内容 创建ppt文档 安装 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple python…...
计算机网络-网络层,运输层,应用层
网络层/网际层 网络层的主要任务包括: 提供逻辑上的端到端通信:网络层负责确定数据的传输路径,使数据能够从源主机传输到目标主机,即实现端到端的通信。数据包的路由和转发:网络层根据目标主机的地址信息,…...

Python爬虫学习
1.1搭建爬虫程序开发环境 爬取未来七天天气预报 from bs4 import BeautifulSoup from bs4 import UnicodeDammit import urllib.request url"http://www.weather.com.cn/weather/101120901.shtml" try:headers{"User-Agent":"Mozilla/5.0 (Windows …...

台式电脑黑屏无法开机怎么办 电脑开机黑屏的解决方法
经常有朋友电脑一开机,发现电脑黑屏没法用了。很多人看到黑屏就懵了,以为电脑要报废了,这是什么原因?电脑开机黑屏怎么解决?一般常说的黑屏故障分为两种,显示屏没有任何显示以及显示英文。下面小编要为大家带来的是台式电脑黑屏…...

【Docker】初学者 Docker 基础操作指南:从拉取镜像到运行、停止、删除容器
在现代软件开发和部署中,容器化技术已经成为一种常见的方式,它能够提供一种轻量级、可移植和可扩展的应用程序打包和部署解决方案。Docker 是目前最流行的容器化平台之一,它提供了一整套工具和技术,使得容器的创建、运行和管理变得…...
))
突破编程_C++_面试(数组(1))
面试题1:详细说明一下数组名是什么? 在 C 中,数组名代表数组首元素的地址。更具体地说,数组名是一个指向数组第一个元素的常量指针。这意味着,当使用数组名时,实际上是在使用指向数组第一个元素的指针。 例…...
基于springboot+vue的靓车汽车销售网站(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
【知识整理】Git Commit Message 规范
一. 概述 前面咱们整理过 Code Review 一文,提到了 Review 的重要性,已经同过gitlab进行CodeReview 的方式,那么本文详细说明一下对CodeReivew非常重要的Git Commit Message 规范。 我们在每次提交代码时,都需要编写 Commit Mes…...
HarmonyOS学习--三方库
文章目录 一、三方库获取二、常用的三方库1. UI库:2. 网络库:3. 动画库: 三、使用开源三方库1. 安装与卸载2. 使用 四、问题解决1. zsh: command not found: ohpm 一、三方库获取 在Gitee网站中获取 搜索OpenHarmony-TPC仓库,在t…...
【服务器数据恢复】FreeNAS+ESXi虚拟机数据恢复案例
服务器数据恢复环境: 一台服务器通过FreeNAS(本案例使用的是UFS2文件系统)实现iSCSI存储,整个UFS2文件系统作为一个文件挂载到ESXi虚拟化系统(安装在另外2台服务器上)上。该虚拟化系统一共有5台虚拟机&…...
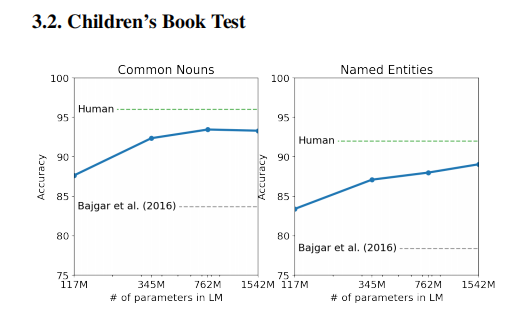
【GPT-2】论文解读:Language Models are Unsupervised Multitask Learners
文章目录 介绍zero-shot learning 零样本学习 方法数据Input Representation 结果 论文:Language Models are Unsupervised Multitask Learners 作者:Alec Radford, Jeff Wu, Rewon Child, D. Luan, Dario Amodei, I. Sutskever 时间:2019 介…...
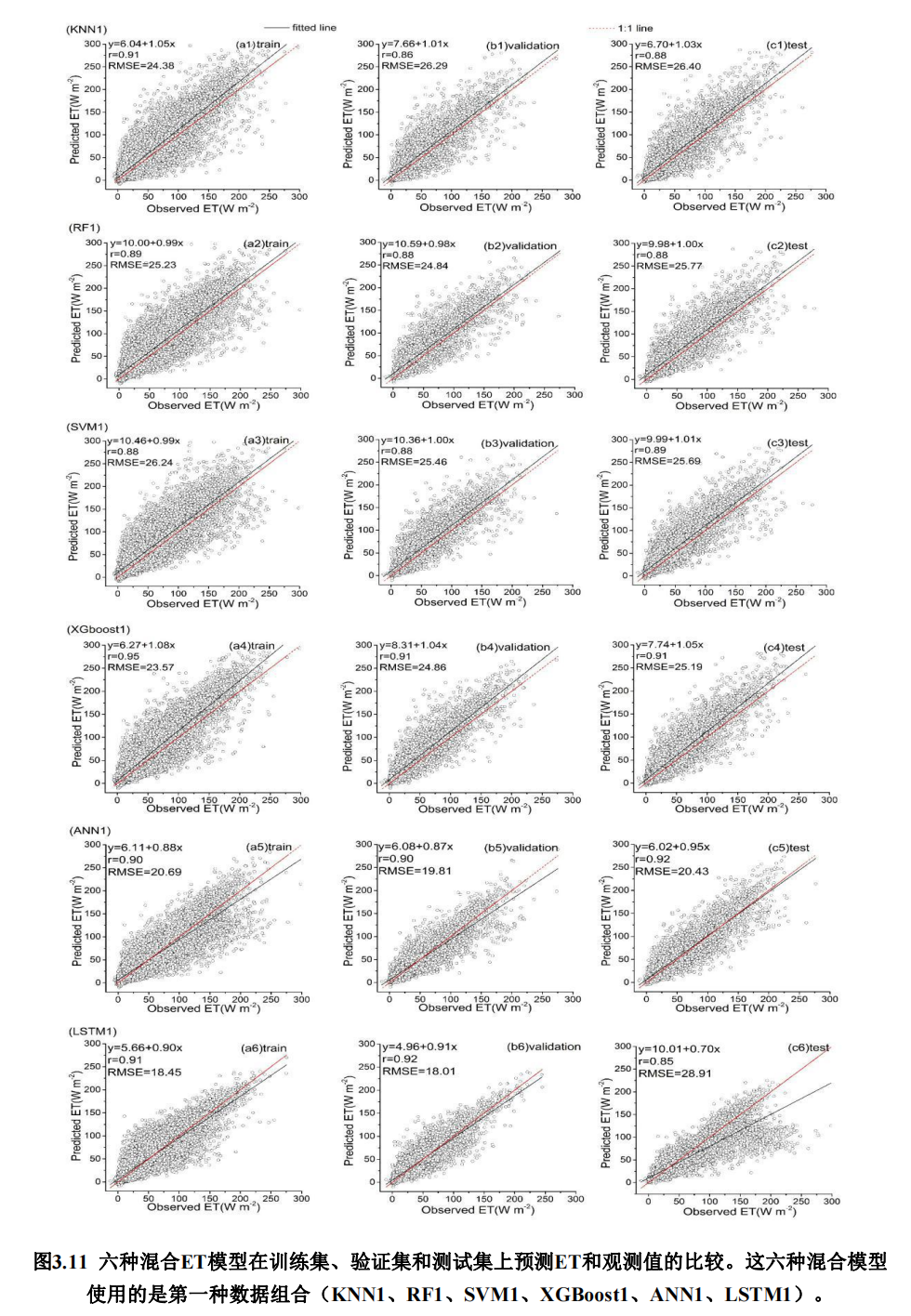
基于机器学习、遥感和Penman-Monteith方程的农田蒸散发混合模型研究_刘燕_2022
基于机器学习、遥感和Penman-Monteith方程的农田蒸散发混合模型研究_刘燕_2022 摘要关键词 1 绪论2 数据与方法2.1 数据2.2 机器学习算法2.3 Penman-Monteith方程2.4 Medlyn公式2.5 模型性能评估 3 基于机器学习算法的混合模型估算农田蒸散量的评价与比较4 利用人工神经网络算法…...
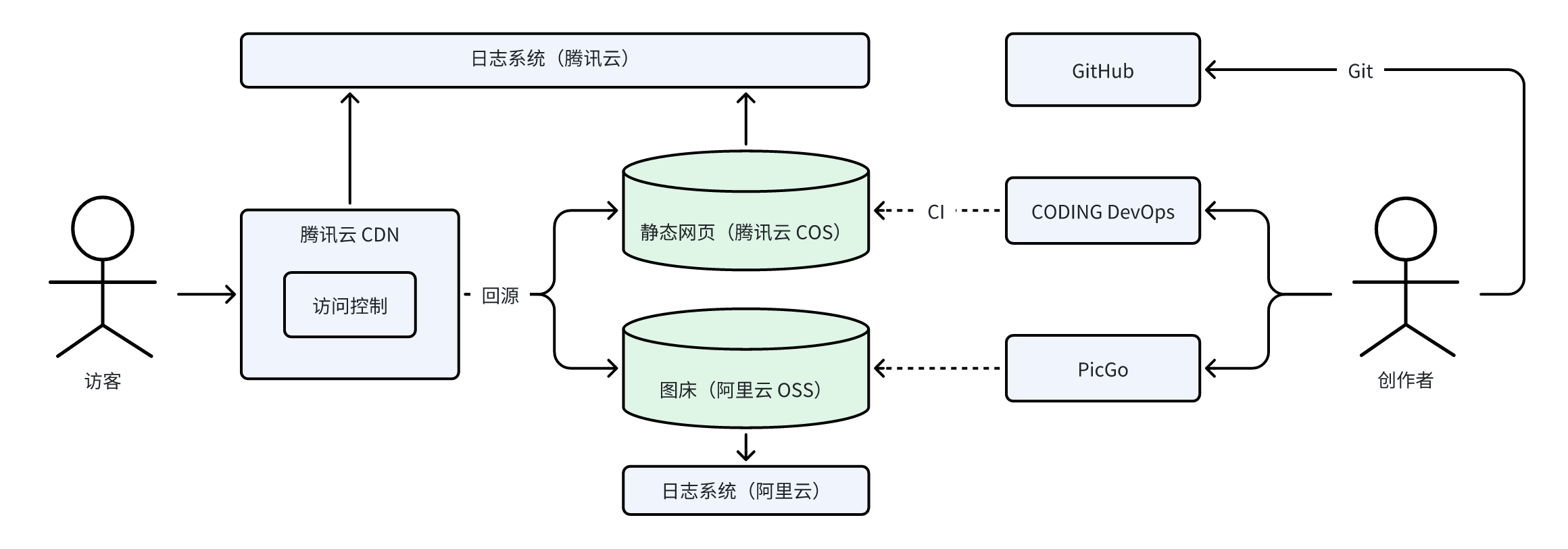
博客 cn 站搭建 v3 v3.1
1. 架构设计 v3.1 版本 2. v2.x 存在的痛点 在v2.x版本中,围绕 服务器 遇到了两个主要的问题: 服务器成本高:博客以静态页面为主,理论上可以实现无服务器部署,但是为了防止恶意攻击,不得不使用服务器进…...
2024全国水科技大会暨流域水环境治理与水生态修复论坛(六)
论坛召集人 冯慧娟 中国环境科学研究院流域中心研究员 刘 春 河北科技大学环境与工程学院院长、教授 一、会议背景 为深入贯彻“山水林田湖是一个生命共同体”的重要指示精神,大力实施生态优先绿色发展战略,积极践行人、水、自然和谐共生理念&…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
