【MySQL】事务的一致性究竟怎么理解?
众所周知,事务有四大特性:原子性、一致性、隔离性、持久性,除了一致性,其他三类特性都很好理解。而关于一致性的解释有点让人头疼,我查了很多文章,大多类似:事务的执行必须使数据库处于一致状态(不能破坏完整性约束)。
我想知道一致性,你却给我抛了一个一致的概念,很让人头疼。但是,功夫不负有心人,结合自身经历,我还是搞出来了让小白很容易看懂解释。
1.正式陈述:事务的一致性是指,事务的执行必须使得数据库从一个一致状态转换到另一个一致状态,这里的一致状态是指:数据库中的所有数据都是已完成的事务提交后的结果。
2.解释
由于在开发中,要保证数据库中的数据不会出错,必须用到事务管理。管理的是对数据库进行了增删改查的业务。因此,后端开发中的事务可简洁理解为:SQL语句的集合。
由于事务的原子特性,当一个事务执行结束时,其中包含的SQL要么全部执行、要么全部不执行,这就保证了上文所说的:数据库中所有数据都是已执行完成的事务提交后的结果。换句话说,事务的原子性成就了事务的一致性。
上述就是事务的一致性,但就理解来看,需要结合数据库的一致状态,否则无法凭事务具有一致性这个词汇本身进行剖析,因为“事务的一致性“中的"一致性",是指事务作用于数据库之后,数据库呈现出的状态,而不是事务的状态。
相关文章:

【MySQL】事务的一致性究竟怎么理解?
众所周知,事务有四大特性:原子性、一致性、隔离性、持久性,除了一致性,其他三类特性都很好理解。而关于一致性的解释有点让人头疼,我查了很多文章,大多类似:事务的执行必须使数据库处于一致状态…...

证件照(兼容H5,APP,小程序)
证件照由uniappuyui开发完成,并同时兼容H5、App、微信小程序、支付宝小程序,其他端暂未测试。 先看部分效果图吧具体可以下方复制链接体验demo 首页代码 <template><view class""><view class"uy-m-x-30 uy-m-b-20"…...

pytorch-textregression,中文文本回归实践,支持多值输出
pytorch-textregression,中文文本回归实践,支持多值输出 pytorch-textregression是一个以pytorch和transformers为基础,专注于中文文本回归的轻量级自然语言处理工具,支持多值回归等。 目录 数据使用方式paper参考 项目地址 py…...

go语言学而思【持续更新】
问题:在Go语言中nil是什么意思? 答:在Go语言中,nil是一个预声明的标识符,用于表示某些类型的零值。它可以被用作以下类型的零值: 指针(Pointer)切片(Slice)…...
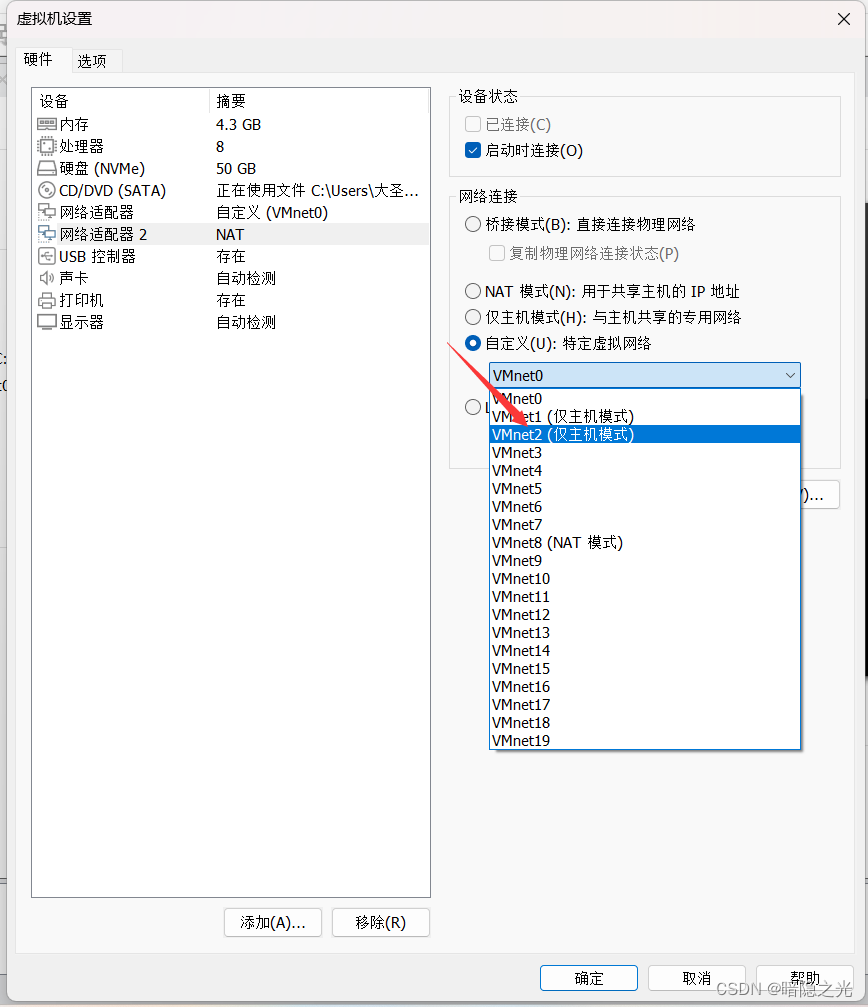
LVS-NAT之VMNET环境搭建
目录 搭建拓扑图 搭建规划 VMNET0 搭建 VMNET2 搭建 LVS端增加网卡 搭建拓扑图: 搭建规划: CLIENT(servera): VMNET0 LVS(serverb): VMNET0 VMNET2 WEB1(serverd): VMNET2 WEB2(servere): VMNET2 VMNE…...
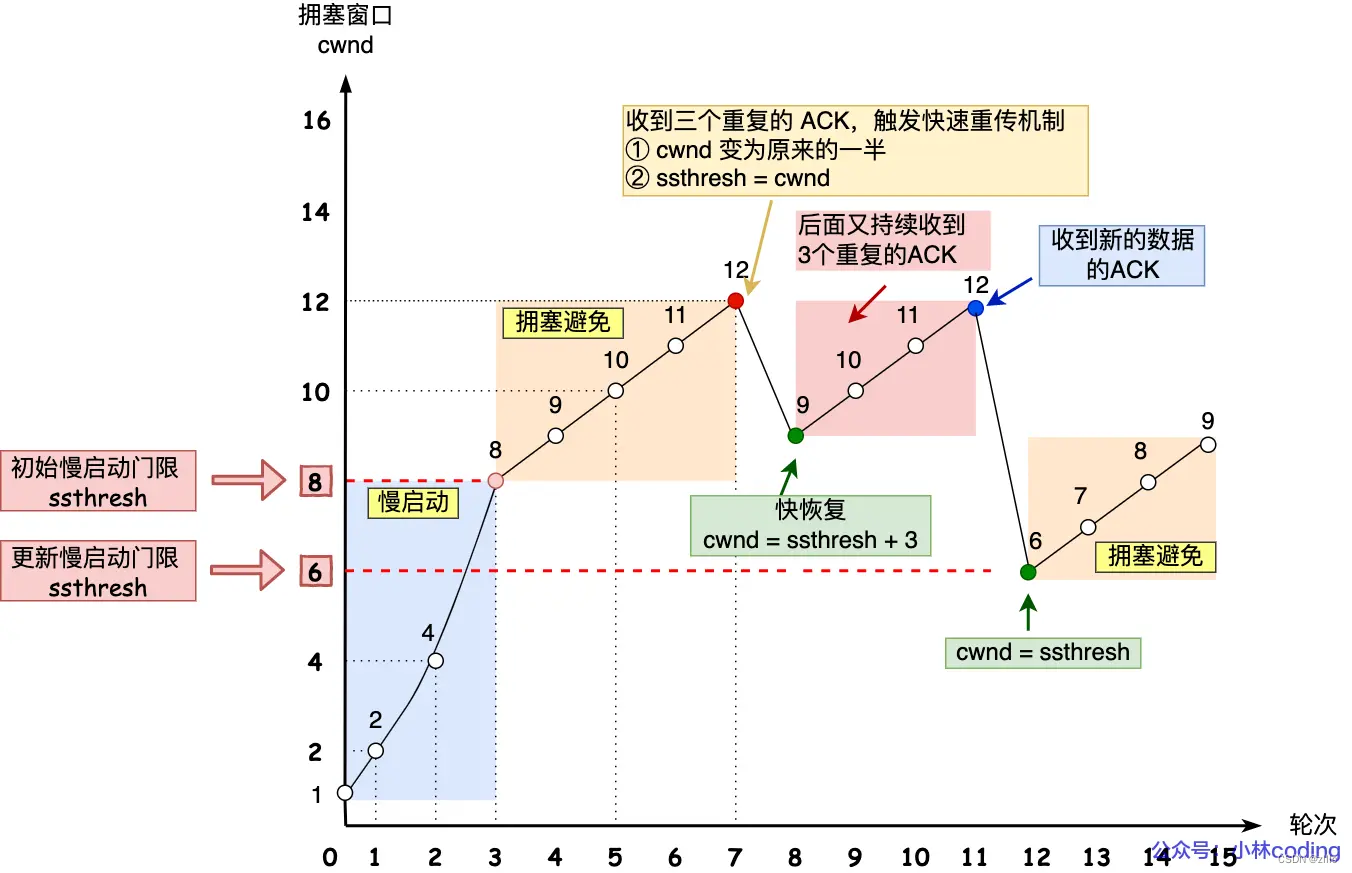
[TCP] TCP/IP 基础知识词典(2)
我想统计一下,TCP/IP 尤其是TCP协议,能搜到的常见的问题,整理起来,关键词添加在目录中,便于以后查阅。 目前预计整理共3篇: [TCP] TCP/IP 基础知识问答 :基础知识 [TCP] TCP/IP 基础知识问答&…...

【牛牛送书 | 第四期】《高效使用Redis:一书学透数据存储与高可用集群》带你快速学习使用Redis
前言: 当今互联网技术日新月异,随着数据量的爆炸式增长,如何高效地存储和管理数据成为了每个公司都必须面对的挑战。与此同时,用户对于应用程序的响应速度和稳定性要求也越来越高。在这个背景下,Redis 作为一个…...
Threejs 实现3D影像地图,Json地图,地图下钻
1.使用threejs实现3D影像地图效果,整体效果看起来还可以,底层抽象了基类,实现了通用,对任意省份,城市都可以只替换数据,即可轻松实现效果。 效果如下: 链接https://www.bilibili.com/video/BV1…...
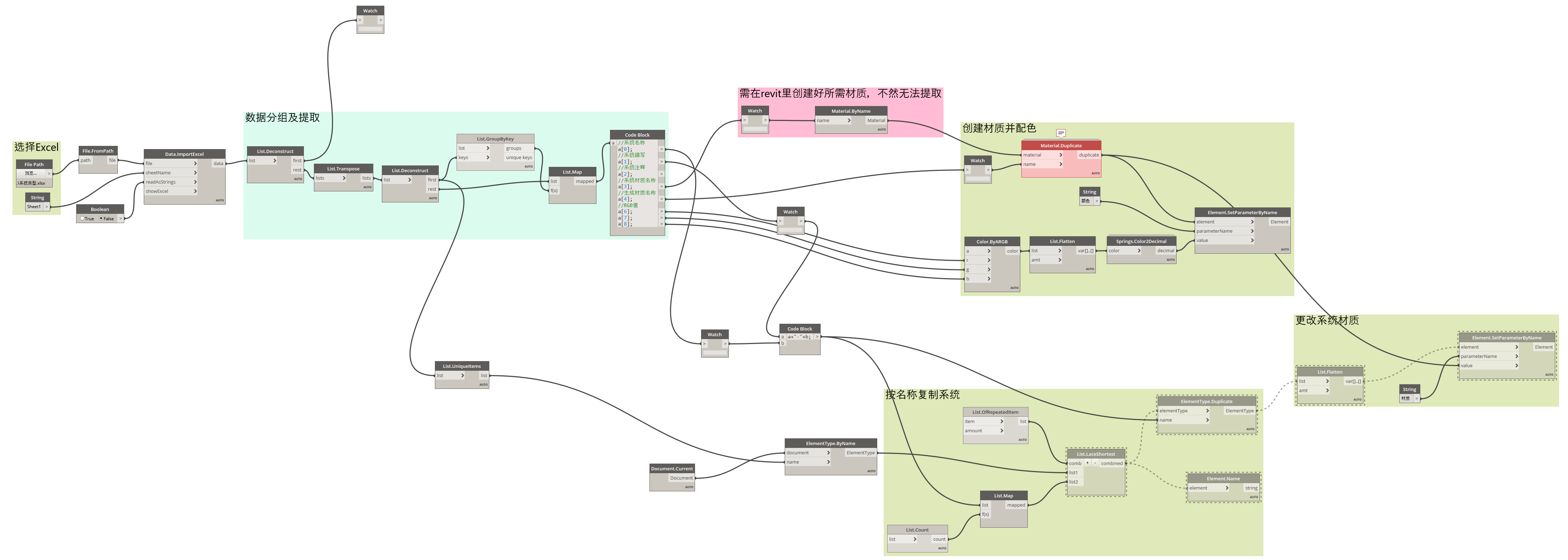
根据Excel创建管道系统及材质
之前看过程鑫老师的文章,介绍过根据Excel数据创建管道系统,但是有小伙伴问过我,照着他这个做,没成功,于是呢,我就想试下,结果发现也没成功。 然后我逐个节点过了一遍,发现可能是因为…...

第八篇【传奇开心果系列】python的文本和语音相互转换库技术点案例示例:Google Text-to-Speech虚拟现实(VR)沉浸式体验经典案例
传奇开心果博文系列 系列博文目录python的文本和语音相互转换库技术点案例示例系列 博文目录前言一、雏形示例代码二、扩展思路介绍三、虚拟导游示例代码四、交互式学习示例代码五、虚拟角色对话示例代码六、辅助用户界面示例代码七、实时语音交互示例代码八、多语言支持示例代…...
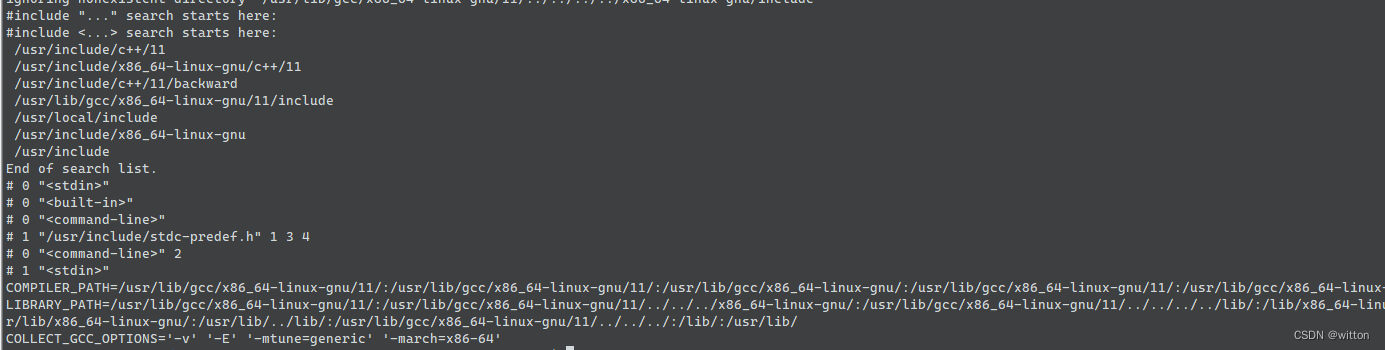
ubuntu使用LLVM官方发布的tar.xz来安装Clang编译器
ubuntu系统上的软件相比CentOS更新还是比较快的,但是还是难免有一些软件更新得不那么快,比如LLVM Clang编译器,目前ubuntu 22.04版本最高还只能安装LLVM 15,而LLVM 18 rc版本都出来了。参见https://github.com/llvm/llvm-project/…...

Windows 远程控制 Mac 电脑怎么操作
要从 Windows 远程控制 Mac 电脑,您可以使用内置 macOS 功能或第三方软件解决方案。以下是一些方法: 一、使用内置 macOS 功能(屏幕共享) 1、在 macOS 上启用屏幕共享 转至系统偏好设置 > 共享;选中“屏幕共享”…...

c# HttpCookie操作,建立cookie工具类
HttpCookie 是一个在.NET Framework中用于管理和操作HTTP Cookie的类。它提供了一种方便的方式来创建、设置、读取和删除Cookie。 Cookie是一种在客户端和服务器之间传递数据的机制,用于跟踪用户的会话状态和存储用户相关的信息。它通常由服务器发送给客户端&#…...

【这个词(Sequence-to-Sequence)在深度学习中怎么解释,有什么作用?】
🚀 作者 :“码上有前” 🚀 文章简介 :深度学习笔记 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 Sequence-to-Sequence(Seq2Seq) Sequence-to-Sequence(Seq2Seq…...

挑战30天学完Python:Day16 日期时间
📘 Day 16 🎉 本系列为Python基础学习,原稿来源于 30-Days-Of-Python 英文项目,大奇主要是对其本地化翻译、逐条验证和补充,想通过30天完成正儿八经的系统化实践。此系列适合零基础同学,或仅了解Python一点…...

Web3之光:揭秘数字创新的未来
随着数字化时代的深入发展,Web3正以其独特的技术和理念,为我们打开数字创新的崭新视角。作为数字化时代的新兴力量,Web3将深刻影响着我们的生活、工作和社会。本文将揭秘Web3的奥秘,探讨其在数字创新领域的前景和潜力。 1. 重新定…...
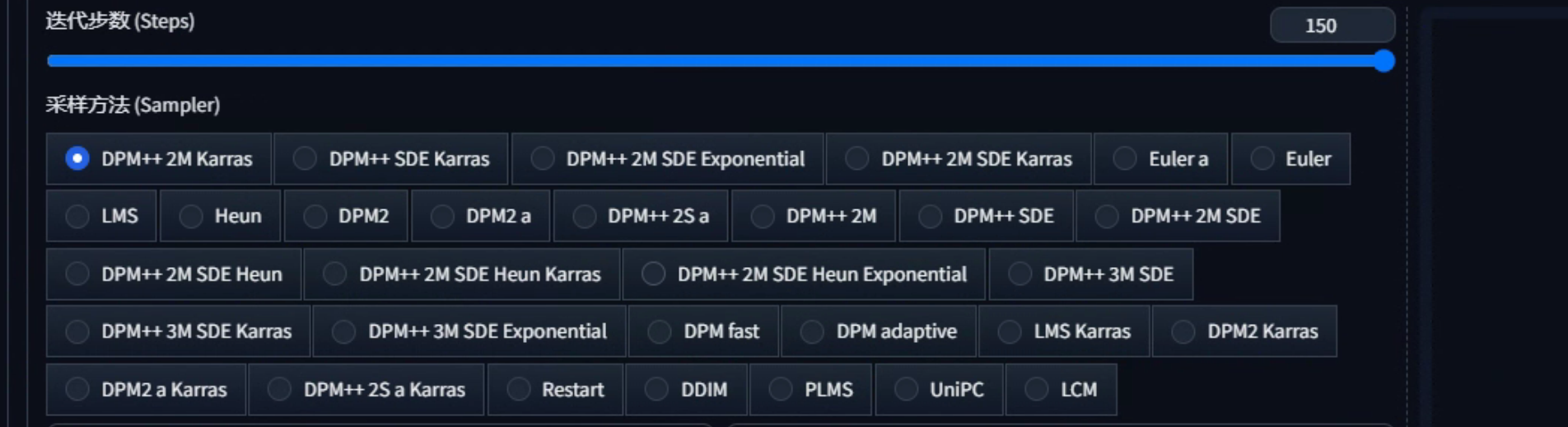
Stable Diffusio——采样方法使用与原理详解
简介 当使用稳定扩散(Stable Diffusion)技术生成图像时,首先会生成一张带有噪声的图像。然后,通过一系列步骤逐渐去除图像中的噪声,这个过程类似于从一块毛坯的白色大理石开始,经过多日的精细雕刻…...

小米14 ULTRA:重新定义手机摄影的新篇章
引言 随着科技的飞速发展,智能手机已经不仅仅是一个通讯工具,它更是我们生活中的一位全能伙伴。作为科技领域的佼佼者,小米公司再次引领潮流,推出了全新旗舰手机——小米14 ULTRA。这款手机不仅在性能上进行了全面升级&am…...

【leetcode热题】路径总和 II
难度: 中等通过率: 38.7%题目链接:. - 力扣(LeetCode) 题目描述 给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。 说明: 叶子节点是指没有子节点的节点。 示例: …...

ChatGPT在数据处理中的应用
ChatGPT在数据处理中的应用 今天的这篇文章,让我不断体会AI的强大,愿人类社会在AI的助力下走向更加灿烂辉煌的明天。 扫描下面二维码注册 数据处理是贯穿整个数据分析过程的关键步骤,主要是对数据进行各种操作,以达到最终的…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
