直接插入排序+希尔排序+冒泡排序+快速排序+选择排序+堆排序+归并排序+基于统计的排序
插入排序:直接插入排序、希尔排序
交换排序:冒泡排序、快速排序
选择排序:简单选择排序、堆排序
其他:归并排序、基于统计的排序
一、直接插入排序
#include<stdio.h>
#include<stdlib.h>
/*
直接插入排序:是就地排序,是稳定的,时间复杂度:O(n^2)
*/
int a[105];
int n;
int main()
{int t;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}//认为:a[1] 是有序区域,a[2---n]是乱序区for(int i=2;i<=n;i++){t=a[i];int j;for(j=i-1;j>=1;j--){if(a[j]>t){a[j+1]=a[j];} else{break;}}a[j+1]=t;} for(int i=1;i<=n;i++){printf("%d ",a[i]);}return 0;
}二、希尔排序
#include<stdio.h>
#include<stdlib.h>
/*
希尔排序:取希尔增量序列时: 是就地排序,不是稳定的,时间复杂度:O(n^2)
*/
int a[105];
int n;
int main()
{int t;scanf("%d",&n);int k=0;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int d=n/2;d>=1;d=d/2) {k++;//计算趟数 //以增量d分组,对每组进行直接插入排序for(int i=1+d;i<=n;i++){t=a[i];int j;for(j=i-d;j>=1;j=j-d){if(a[j]>t){a[j+d]=a[j];}else{break;}}a[j+d]=t; } printf("第%d趟,增量为%d,排好的结果:",k,d);for(int i=1;i<=n;i++){printf("%d ",a[i]);}printf("\n");} return 0;
}三、冒泡排序
#include<stdio.h>
#include<stdlib.h>
#define maxx 100
/*所谓交换,是指根据序列中两个关键字比较的结果来对换这两个关键字在序列中的位置。*/
int a[maxx],n,t;
int v;//标记
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}//冒泡排序//外层循环控制 排序的趟数 n个元素排序需要循环n-1次 【1】for(int i=1;i<=n-1;i++) {v=0;//内层循环控制比较的次数 n个元素第i趟比较n-i次 【2】for(int j=1;j<n-i+1;j++) {//比较相邻的元素大小 目的:将最大的元素选出到移动到最后 if(a[j]>a[j+1]){v=1;t = a[j];a[j] = a[j+1];a[j+1] = t;}}if(v==0)//v仍然等0,说明没交换,说明完全有序 {break;}}for(int i=1;i<=n;i++){printf("%d ",a[i]);}return 0;
}四、快速排序
排序区间[l,r] , 选 a[l] 做基准数
两个下标i=l,j=r;相对遍历。
先用j 找一个比x小的数,放在i位置,i++
再用i 找一个比x大的数,放在j位置,j--
不断循环,直到 i==j为止,此时i(j)位置就是x的位置
#include<stdio.h>
#include<stdlib.h>
/*交换排序:基于数据交换的排序
1.冒泡排序:是就地排序, 是稳定的,时间复杂度 O(n^2) 2.快速排序:---递归: 是就地排序,不稳定,时间复杂度O(nlogn) ------待排序的数组已经保持需要的顺序了,容易退化成O(n^2)
每一趟:先选一个标准(基准数),按照基准数进行划分,把比基准数小的交换到他前面,
把比基准数大的交换到他后面 基准数怎么选:对区间(l,r)
(1)选排序区间的第一个数--a[l]------为例
(2)选排序区间的最后一个数--a[r]
*/
void QuickSort(int a[],int l,int r)
{//选排序区间的第一个数--a[l]做基准数if(l>=r){return;} int x=a[l];int i=l;int j=r; while(i<j){//先 从后往前,找一个小于基准数小的数,放到i位置 while(i<j&&a[j]>x)j--; if(i<j){a[i]=a[j];i++;} //再从前往后,找一个小于基准数大的数,放到j位置while(i<j&&a[i]<x)i++; if(i<j){a[j]=a[i];j--;} }a[i]=x;QuickSort(a,l,i-1); QuickSort(a,i+1,r);
}int main()
{int a[105]; int n;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}//快速排序QuickSort(a,1,n); for(int i=1;i<=n;i++){printf("%d ",a[i]);}printf("\n");return 0;
}五、(简单)选择排序
每趟从待排序区中,选择一个最小的数,放到待排序区的第一个位置。从而实现排序
#include<stdio.h>
#include<stdlib.h>
#define maxx 100int a[maxx],n,t;
int minn; int main()
{int minn;//最小元素的下标 scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}//简单选择排序:就地排序, 时间复杂度O(n^2) ,不稳定的排序 //简单选择排序:进行n-1趟排序,每次都在乱序区中选择一个最小的元素,放在乱序的第一个位置,此时有序区+1,乱序区-1 for(int i=1;i<=n-1;i++)//控制循环趟数{minn=i; for(int j=i+1;j<=n;j++)//控制乱序区,去找最小的元素的位置{if(a[j]<a[minn]){minn=j;}}//把minn位置的元素放在乱序区的第一个位置,即i位置if(minn!=i){int t=a[i];a[i]=a[minn];a[minn]=t; }} for(int i=1;i<=n;i++){printf("%d ",a[i]);}printf("\n");return 0;
}六、堆排序
堆----->完全二叉树----->数组存储
a[i]父亲:a[i/2]
a[i]左孩子:a[2*i]
a[i]右孩子:a[2*i+1]
1.建堆(两种方法)
(1)自我初始化:在原数组的基础上进行初始化
从子树入手由小到大去调整每棵子树;
对于每棵子树,我们向下调整:
让根节点和左右孩子节点作比较,如果子树值小:最小值和根节点交换,继续向下调整子树
(2)通过插入来建堆
数组每多一个数据就调整一次。新插入的数据放在放在最后,如果其比父亲大或者新插入的数据是根节点就不用调整否则就向上调整
堆排序:
(1)建堆(流程见上)
(2)循环n次 每次输出最小的数---->a[1],
删掉a[1]--->让堆中最后一个节点来替换a[1],然后重新对a[1]向下调整
#include<stdio.h>
#include<stdlib.h>
#define maxx 100/*升序排列 堆排序:就地排序,不稳定 ,时间复杂度O(nlogn) n个元素,保存在a数组中,直接在a数组中
1.初始化成一个小顶堆:下标最大的内部节点的下标是几?最后一个内部节点的下标是几?n/2
(1)找到最后一个内部节点(n/2),依次调整每棵子树调整过程:依次向下比较调整:若该节点比左右孩子节点中的最小值大,进行交换,直到不满足该条件位置
2.在小顶堆的基础上,进行堆排序循环n-1次:(1)输出(删除)根节点;(2)最后一个位置的节点代替根节点
(3)向下调整
---输入最后一个元素
3.堆中插入一个元素:
(1)把元素放到数组最后
(2)向上和父亲节点比较进行调整*/
void downAdjust(int a[],int i,int m)//对以 下标i的元素 为根节点的子树进行向下调整
{//now是当前调整的节点,next是now的孩子,也是下一次要调整的节点 int now=i;int next;int t;while(now*2<=m){next=now*2;//now的左孩子if(next+1<=m&&a[next+1]<a[next]){next=next+1;//now的右孩子 }if(a[now]<=a[next]){break;} else{t=a[now];a[now]=a[next];a[next]=t;now=next;}} }
void upAdjust(int a[],int n)
{//now是当前调整的节点,next是now的父亲,也是下一次要调整的节点int now=n;int next; int t;while(now>1){next=now/2;// now的父亲if(a[next]<=a[now])//父亲节点比当前节点大 {break;}else{t=a[now];a[now]=a[next];a[next]=t;now=next;}} } int main()
{int n;//元素个数int a[maxx];// scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}
//把a数组初始化成小顶堆for(int i=n/2;i>=1;i--){downAdjust(a,i,n);}
//堆排序int m=n;//数组最后一个元素下标 int t;for(int i=1;i<=n;i++){printf("%d ",a[1]);t=a[1];a[1]=a[m];a[m]=t;m--;downAdjust(a,1,m);} printf("\n");for(int i=1;i<=n;i++){printf("%d ",a[i]);}printf("\n");
//在堆中插入一个元素;n++;scanf("%d",&a[n]);upAdjust(a,n);return 0;
}//堆的应用--优先队列 七、归并排序
#include<stdio.h>
#include<stdlib.h>
#define maxx 100
void merge(int a[],int l,int mid,int r)
{//l~mid//mid+1~rint t[maxx];int k=0;//t数组的下标 int i=l;int j=mid+1;while(i<=mid&&j<=r){if(a[i]<=a[j]){t[k]=a[i]; k++;i++;}else{t[k]=a[j];k++;j++;}}while(i<=mid){t[k]=a[i]; k++;i++;}while(j<=r){t[k]=a[j]; k++;j++;}for(int i=0;i<k;i++){a[l+i]=t[i];}}void merge_sort(int a[],int l,int r)
{int mid;if(l<r){mid=(l+r)/2;//l~midmerge_sort(a,l,mid);//mid+1~rmerge_sort(a,mid+1,r);merge(a,l,mid,r);}}
int main()
{int n;//元素个数int a[maxx];// scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}merge_sort(a,1,n);for(int i=1;i<=n;i++){printf("%d ",a[i]);}printf("\n");return 0;
}八、基于统计的排序
1.计数排序
统计一下每个数出现的次数,然后直接按次数输出即可(以空间换时间的算法)
缺点:
a.无法对负整数进行排序(偏移量优化)
b.极其浪费内存空间
c.是一个不稳定排序(可优化)
2.桶排序
1、将代排序的序列部分分到若⼲个桶中,每个桶内的元素再进⾏个别的排序。
2、时间复杂度最好可能是线性的O(n),桶排序不是基于⽐较的排序
3.基数排序
略
相关文章:

直接插入排序+希尔排序+冒泡排序+快速排序+选择排序+堆排序+归并排序+基于统计的排序
插入排序:直接插入排序、希尔排序 交换排序:冒泡排序、快速排序 选择排序:简单选择排序、堆排序 其他:归并排序、基于统计的排序 一、直接插入排序 #include<stdio.h> #include<stdlib.h> /* 直接插入排序&#…...
)
Java高级 / 架构师 场景方案 面试题(二)
1.双十一亿级用户日活统计如何用 Redis快速计算 在双十一这种亿级用户日活统计的场景中,使用Redis进行快速计算的关键在于利用Redis的数据结构和原子操作来高效地统计和计算数据。以下是一个基于Redis的日活统计方案: 选择合适的数据结构: …...
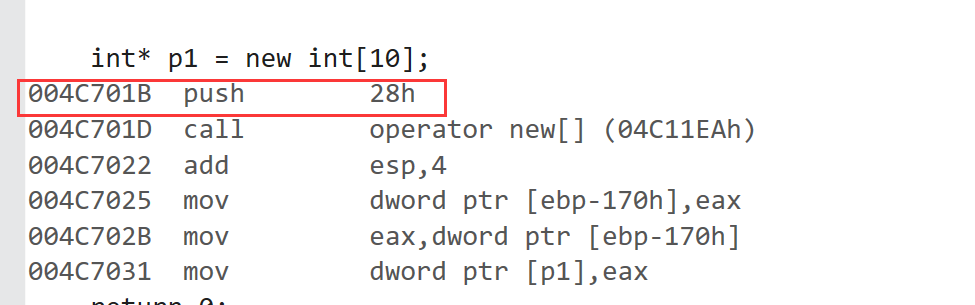
C/C++内存管理学习【new】
文章目录 一、C/C内存分布二、C语言中动态内存管理方式:malloc/calloc/realloc/free三、C内存管理方式3.1 new/delete操作内置类型3.2 new和delete操作自定义类型四、operator new与operator delete函数五、new和delete的实现原理5.1 内置类型 六、定位new表达式(pl…...

选择适合你的编程语言
引言 在当今瞬息万变的技术领域中,选择一门合适的编程语言对于个人职业发展和技术成长至关重要。每种语言都拥有独特的设计哲学、应用场景和市场需求,因此,在决定投入时间和精力去学习哪种编程语言时,我们需要综合分析多个因素&a…...

【力扣每日一题】力扣106从中序和后序遍历序列构造二叉树
题目来源 力扣106从中序和后序遍历序列构造二叉树 题目概述 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 思路分析 后序遍历序列的最末尾数…...

logback日志回滚原理
日志输出主要依赖RollingFileAppender、TimeBasedRollingPolicy、SizeAndTimeBasedFNATP。 RollingFileAppender 主要用于生成日志文件,格式化内容再输出到日志文件TimeBasedRollingPolicy 设置回滚策略,如果发现日志输出的时间超过单位时间,…...

[C#]winform基于opencvsharp结合pairlie算法实现低光图像增强黑暗图片变亮变清晰
【低光图像增强介绍】 在图像处理领域,低光图像增强是一个具有挑战性的任务。由于光线不足,这些图像往往呈现出低对比度、高噪声和细节丢失等问题,严重影响了图像的视觉效果和后续分析的准确性。因此,开发有效的低光图像增强方法…...
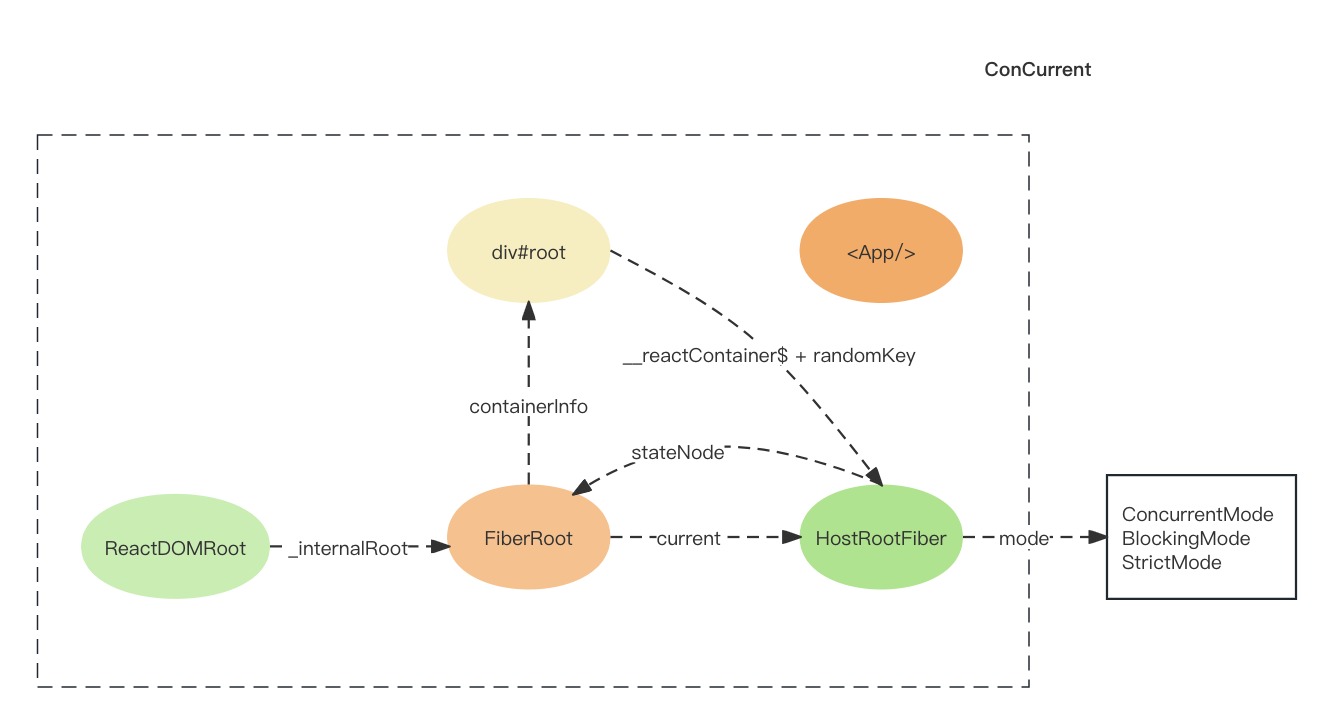
React18源码: reconcliler启动过程
Reconcliler启动过程 Reconcliler启动过程实际就是React的启动过程位于react-dom包,衔接reconciler运作流程中的输入步骤.在调用入口函数之前,reactElement(<App/>) 和 DOM对象 div#root 之间没有关联,用图片表示如下: 在启…...
【RN】为项目使用React Navigation中的navigator
简言 移动应用基本不会只由一个页面组成。管理多个页面的呈现、跳转的组件就是我们通常所说的导航器(navigator)。 React Navigation 提供了简单易用的跨平台导航方案,在 iOS 和 Android 上都可以进行翻页式、tab 选项卡式和抽屉式的导航布局…...

CS50x 2024 - Lecture 8 - HTML, CSS, JavaScript
00:00:00 - Introduction 关于互联网是怎么工作的,如何在他的基础上构建软件 HTML和CSS是描述性语言 javascript一种编程语言,在浏览器上下文中很有用,使得界面更具交互性,也用于服务器 00:01:01 - Bingo Board 00:01:51 - T…...
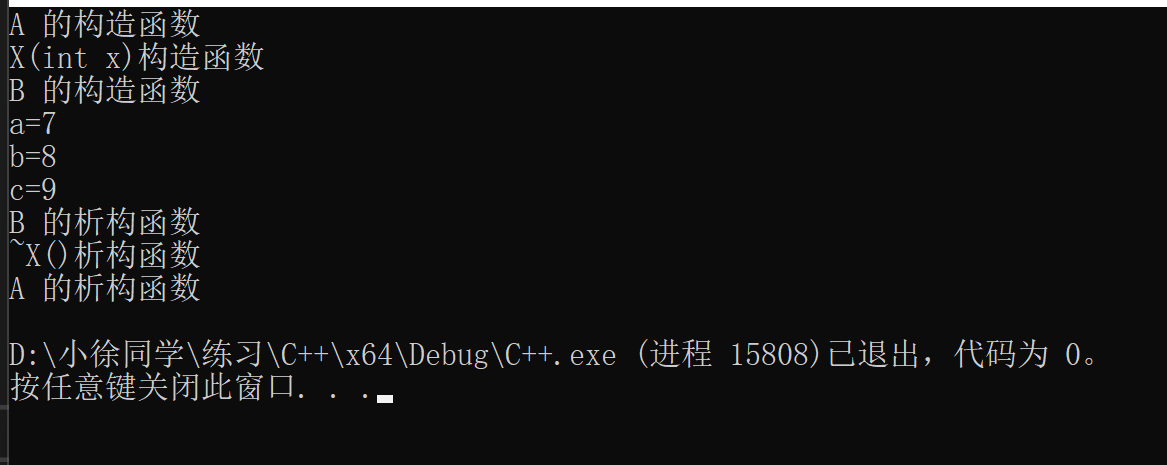
C++:派生类的生成过程(构造、析构)
目录 派生类的生成过程 派生类的构造函数与析构函数: 构造函数: 派生类组合类的构造和析构: 构造函数和析构函数调用顺序: 派生类的生成过程 三步骤: 吸收基类(父类)成员:实现代…...

金蝶字段添加过滤条件
金蝶字段加过滤条件 F_PLDE_Date<GetValue(FDate) and F_PLDE_Date1>GetValue(FDate)...

SQLite 知识整理
写在前面: 本文章旨在总结备份、方便以后查询,由于是个人总结,如有不对,欢迎指正;另外,内容大部分来自网络、书籍、和各类手册,如若侵权请告知,马上删帖致歉。 目录 SQLite 类型数据…...
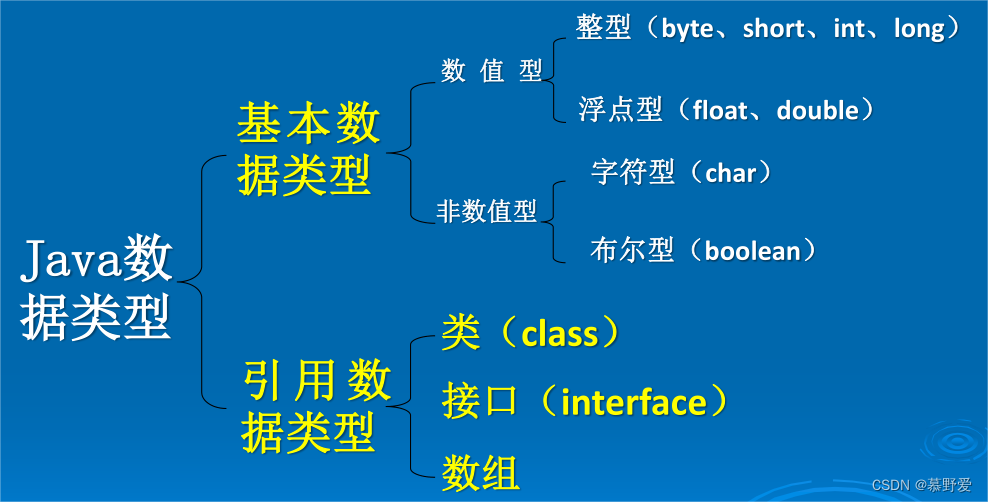
0基础JAVA期末复习最终版
啊啊啊啊啊啊啊啊啊啊,根据网上各位大佬的复习资料,看了很多大多讲的是基础但对内容的整体把握上缺乏系统了解。但是很不幸最终挂科了,那个出题套路属实把我整神了,所以我决定痛改前非,酣畅淋漓的写下这篇文章。。。。…...
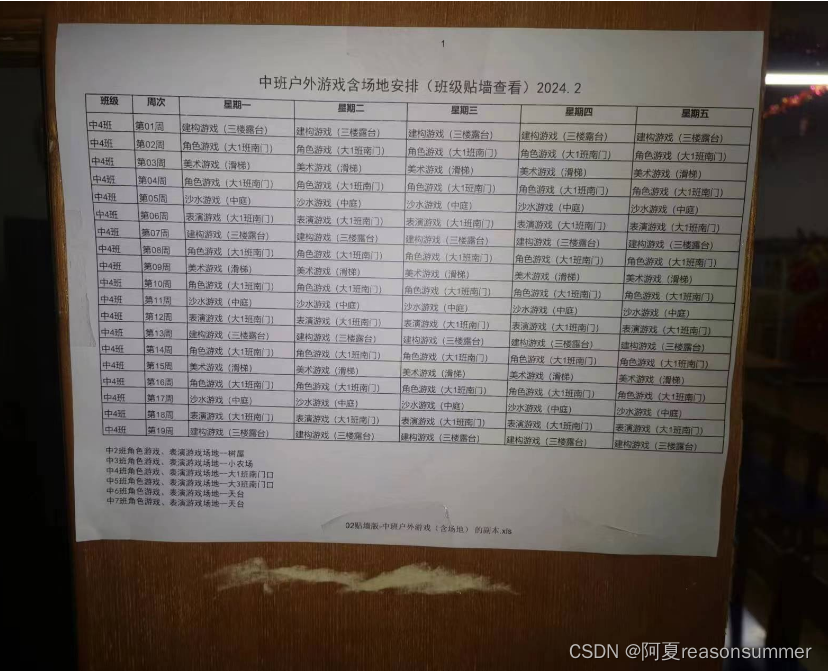
【办公类-16-07-04】合并版“2023下学期 中班户外游戏(有场地和无场地版,一周一次)”(python 排班表系列)
背景需求: 把 无场地版(贴周计划用) 和 有场地版(贴教室墙壁上用) 组合在一起,一个代码生成两套。 【办公类-16-07-02】“2023下学期 周计划-户外游戏 每班1周五天相同场地,6周一次循环”&…...

chat GPT第一讲
计算机的语言奇迹:探秘ChatGPT的智能回答和写作能力 目前我们这个行业,最火的话题无疑是AI人工智能,类似ChatGPT这样的智能Ai,今天剩下的时间不多,每天一个主题,我给大家讲一下计算机回答问题和写作的能力,…...
JAVA工程师面试专题-Mysql篇
一、基础 1、mysql可以使用多少列创建索引? 16 2、mysql常用的存储引擎有哪些 存储引擎Storage engine:MySQL中的数据、索引以及其他对象是如何存储的,是一套文件系统的实现。常用的存储引擎有以下: Innodb引擎:In…...

vue中使用echarts绘制双Y轴图表时,刻度没有对齐的两种解决方法
文章目录 1、原因2、思路3、解决方法3.1、使用alignTicks解决3.2、结合min和max属性去配置interval属性1、首先固定两边的分隔的段数。2、结合min和max属性去配置interval。 1、原因 刻度在显示时,分割段数不一样,导致左右的刻度线不一致,不…...

编程笔记 Golang基础 022 数组
编程笔记 Golang基础 022 数组 一、数组定义和初始化二、访问数组元素三、遍历数组四、数组作为参数六、特点七、注意事项 在Go语言中,数组是一种基本的数据结构,用于存储相同类型且长度固定的元素序列。 一、数组定义和初始化 // 声明并初始化一个整数…...
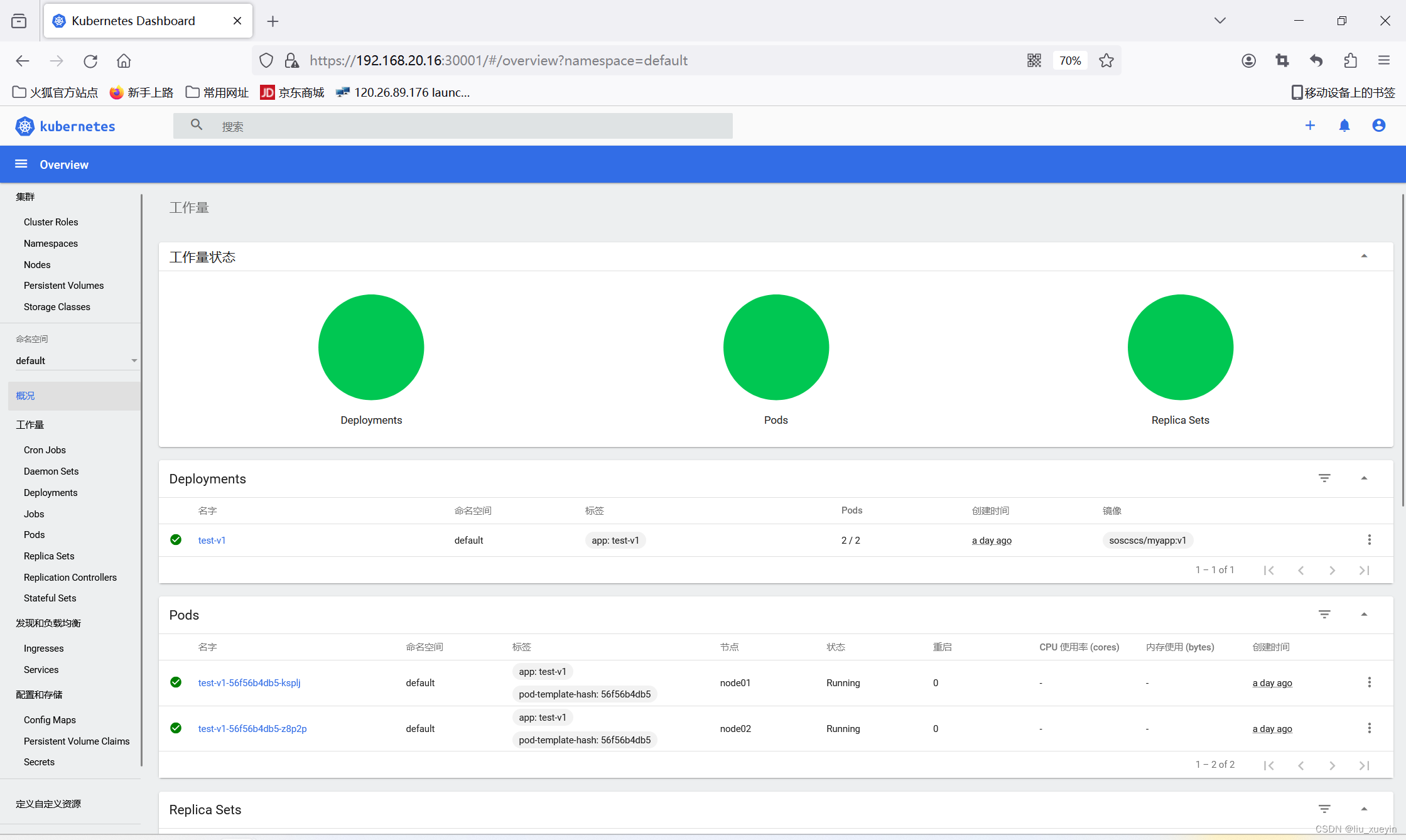
【kubernetes】二进制部署k8s集群之,多master节点负载均衡以及高可用(下)
↑↑↑↑接上一篇继续部署↑↑↑↑ 之前已经完成了单master节点的部署,现在需要完成多master节点以及实现k8s集群的高可用 一、完成master02节点的初始化操作 二、在master01节点基础上,完成master02节点部署 步骤一:准备好master节点所需…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
