(done) 什么是特征值和特征向量?如何求特征值的特征向量 ?如何判断一个矩阵能否相似对角化?
什么是齐次方程? https://blog.csdn.net/shimly123456/article/details/136198159
行列式和是否有解的关系? https://blog.csdn.net/shimly123456/article/details/136198215
特征值和特征向量 参考视频:https://www.bilibili.com/video/BV1vY4y1J7gd/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
一个求特征值和特征向量 (手算,还包括矩阵相似对角化) 的例子:https://www.bilibili.com/video/BV14T4y127jf/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
一个更详细的求特征值和特征向量(手算,提到了“自由未知量”)例子:https://www.bilibili.com/video/BV1Js4y1372V/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600
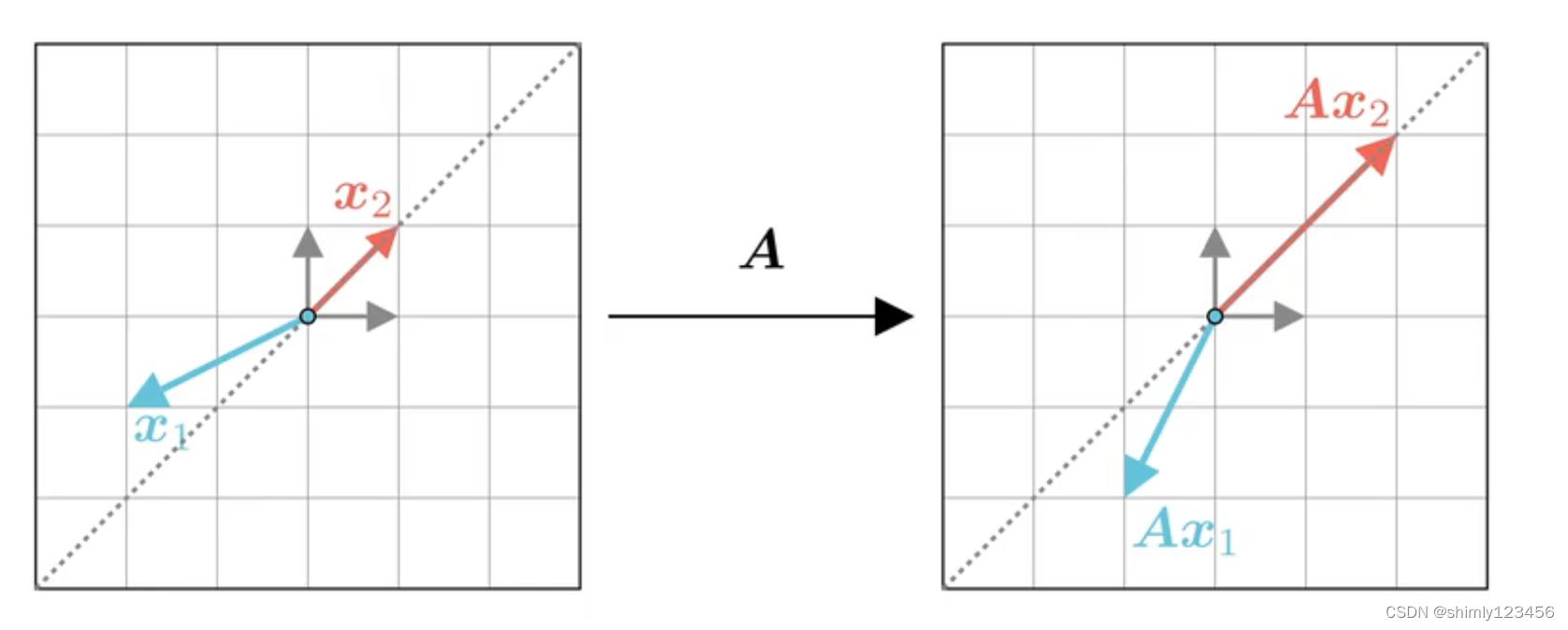
把矩阵 A 作为一个对向量的映射,x1 矢量在经过 A 映射后变换了方向,x2 经过 A 映射后保持原来的方式,只是长度发生了变化 (长度变换可以是负数,也就是 x2 方向变相反了也不影响)。像 x1 这种向量就不是 矩阵A 的特征向量;x2 这种向量就是矩阵 A 的特征向量
由于 矩阵A 对特征向量 x2 只起到了伸缩作用,那么就可以写下式子 (lamda 是一个常数、标量)
Ax2 = (lamda) * x2
在这里,(lamda) 就是特征值,x2 就是特征向量
所以,特征向量的严格定义就是:只要一个向量 x2 可以写成 Ax2 = (lamda) * x2。那么 lamda 就是矩阵 A 的特征值,x2 就是矩阵 A 的特征向量
一个矩阵可以有多个特征值和特征向量,如下图为例:
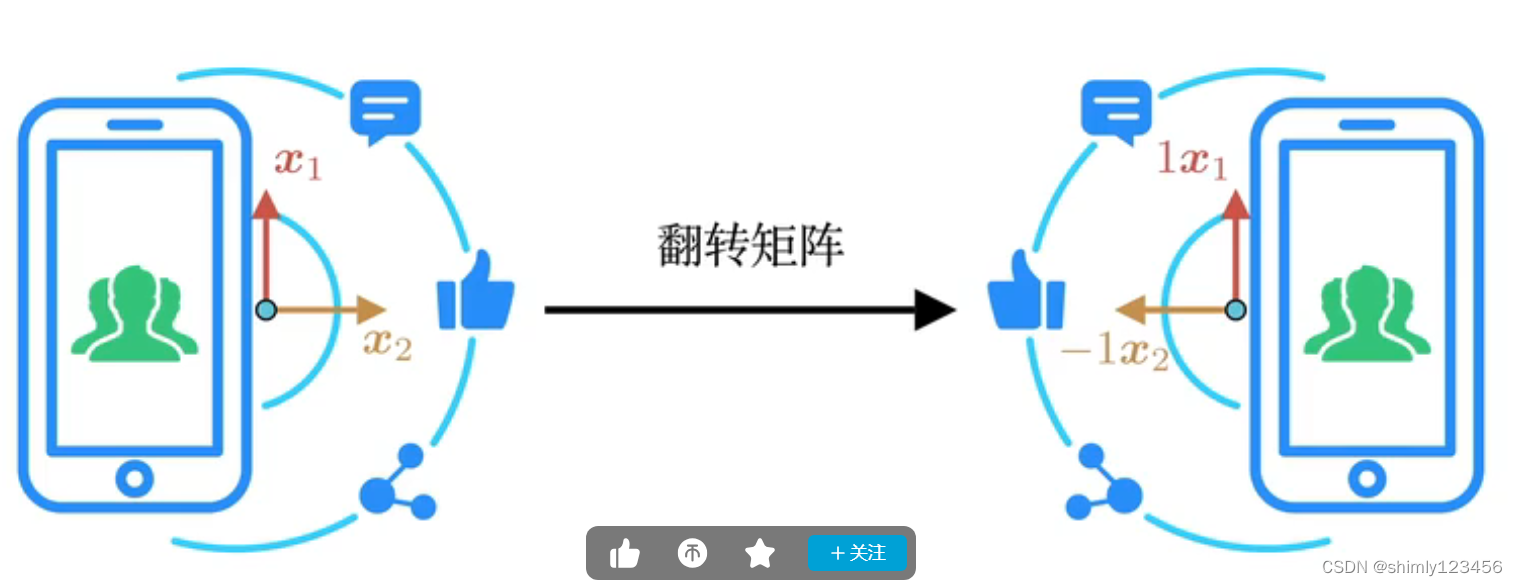
图片可以经过线性变化(或者说,矩阵乘法)进行翻转,只要把图片上的每一个像素点视为一个矢量,然后让它们乘以翻转矩阵即可。
在这里,经过翻转矩阵映射后,图片左右翻转了,每一个像素点(即,矢量) 在纵轴上的方向没有变化,所以有纵特征向量 x1,在横轴上的方向变反了,所以有横特征向量 x2。x1 和 x2 的特征值分别是 1 和 -1
接下来,我们看看特征值和特征向量的严格数学计算

如果看不懂,可以再看一遍参考视频,也就 6min,不长
以下是一个求特征值、特征向量,从而把矩阵相似对角化的例子:

当 lamda1 = lamda2 = 2 时,我们发现求出的矩阵只有一个非零行,那么也就是说它的 “自由未知量” 是 2。
这其实暗含了 “我们能够得到两个线性无关非零解” 的意思,也就说这个矩阵是可以相似对角化的

相关文章:

(done) 什么是特征值和特征向量?如何求特征值的特征向量 ?如何判断一个矩阵能否相似对角化?
什么是齐次方程? https://blog.csdn.net/shimly123456/article/details/136198159 行列式和是否有解的关系? https://blog.csdn.net/shimly123456/article/details/136198215 特征值和特征向量 参考视频:https://www.bilibili.com/video/BV…...
[rust] 11 所有权
文章目录 一 背景二 Stack 和 Heap2.1 Stack2.2 Heap2.3 性能区别2.4 所有权和堆栈 三 所有权原则3.1 变量作用域3.2 String 类型示例 四 变量绑定背后的数据交互4.1 所有权转移4.1.1 基本类型: 拷贝, 不转移所有权4.1.2 分配在 Heap 的类型: 转移所有权 4.2 Clone(深拷贝)4.3 …...
MySQL安装
文章目录 MYSQL安装一、下载二、解压三、配置1. 添加环境变量2. 初始化MySQL3. 注册MySQL服务4. 启动MySQL服务5. 修改默认账户密码 四、登录MySQL五、卸载MySQL MYSQL安装 一、下载 点开下面的链接:https://dev.mysql.com/downloads/mysql/ 点击Download 就可以下…...
AI时代显卡如何选择,B100、H200、L40S、A100、H100、V100 含架构技术和性能对比
AI时代显卡如何选择,B100、H200、L40S、A100、H100、V100 含架构技术和性能对比。 英伟达系列显卡大解析B100、H200、L40S、A100、A800、H100、H800、V100如何选择,含架构技术和性能对比带你解决疑惑。 近期,AIGC领域呈现出一片繁荣景象&a…...

R语言入门笔记2.5
数据预处理 R语言处理的数据多以数据框的形式出现。 预备操作 数据查看 > dim(x) [1] 16 3 #数据框有16行3列 > names(x) #查看数据框的变量名 [1] "X" "Z" "Y" > head(x,3) #查看前3行,若为-3则是查看后三行之…...

命令记录学习
1. 查看当前用户 cat /etc/passwd 添加test用户 useradd test -G root 查看test用户状态 id test 查看用户adaminstrator passwd -S adaminstrator 禁用用户adaminstrator passwd -l adaminstrator 密码策略设置文件地址 vi /etc/pam.d/system-auth 设…...

Python3 TCP 客户端
下面是一个简单的 Python TCP 客户端示例代码,用于与之前提到的 EchoServer 进行通信: import socketserver_address (localhost, 8888)# 创建 TCP 客户端套接字 client_socket socket.socket(socket.AF_INET, socket.SOCK_STREAM)try:# 连接到服务器…...

图论(算法竞赛、蓝桥杯)--拓扑排序
1、B站视频链接:D01 拓扑排序_哔哩哔哩_bilibili #include <bits/stdc.h> using namespace std; const int N100010; int n,m,a,b; vector<int> e[N],tp; int din[N]; bool topsort(){queue<int> q;for(int i1;i<n;i){if(din[i]0)q.push(i);}…...
)
内网穿透(docker部署frp)
文章目录 内网穿透实现内网穿透的常见方法 frpfrp的实现原理frps服务端应用部署配置文件部署参数配置 frpc客户端部署 内网穿透 内网穿透是指在内部网络(内网)中实现穿透外网(公网)的通信。内网通常是指公司、组织或家庭等内部网…...
Java设计模式 | 简介
设计模式的重要性: 软件工程中,设计模式(design pattern)是对软件设计中普遍存在(反复出现)的各种问题,所提出的解决方案。 这个术语由埃里希 伽玛(Erich Gamma)等人在1…...
微信小程序video 点击自动全屏播放
//因为这个地址可能是图片也可能是视频 点击 图片可以预览,点击视频可放大全屏自动播放。 代码如下 <view v-else :class{contentImg: x.picture.length0} style"margin-top: 10px;"v-for"(x1, y1) in x.picture" :key"y"><…...
)
MySQL基础面试问题(一)
MySQL面试问题的标准回答: 什么是数据库范式?MySQL中常见的范式有哪些? 标准回答:数据库范式是一组规则,用于设计关系型数据库的结构,以减少数据冗余和提高数据的一致性。常见的数据库范式包括第一范式&…...
抖音爬虫批量视频提取功能介绍|抖音评论提取工具
抖音爬虫是指通过编程技术从抖音平台上获取视频数据的程序。在进行抖音爬虫时,需要注意遵守相关法律法规和平台规定,以确保数据的合法获取和使用。 一般来说,抖音爬虫可以实现以下功能之一:批量视频提取。这个功能可以用于自动化地…...
mac真的安装不了vmware吗 mac如何安装crossover crossover序列号从哪里买 购买正版渠道
有些用户可能想在mac上运行一些只能在windows上运行的软件,比如游戏、专业软件等。这时候,就需要用到虚拟机技术,也就是在mac上安装一个可以模拟其他操作系统的软件,比如vmware或者crossover。那么,mac真的安装不了vmw…...
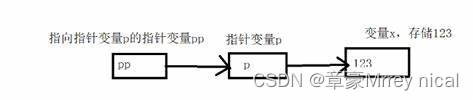
C语言-指针详解速成
1.指针是什么 C语言指针是一种特殊的变量,用于存储内存地址。它可以指向其他变量或者其他数据结构,通过指针可以直接访问或修改存储在指定地址的值。指针可以帮助我们在程序中动态地分配和释放内存,以及进行复杂的数据操作。在C语言中&#…...

C# RabbitMQ使用--动态更新
在使用 RabbitMQ 的 C# 客户端库时,只需要在应用程序中引用 RabbitMQ.Client 包,而不需要单独安装 RabbitMQ 服务器。 RabbitMQ.Client 是一个用于在 C# 中与 RabbitMQ 服务器进行通信的客户端库。通过使用该客户端库,你可以在应用程序中创建…...
Unity资源加密解决方案
据统计,全球范围内超过50%的游戏均使用Unity创作而成,作为游戏开发市场第一大游戏引擎占有者,Unity已经全面覆盖到各个游戏平台。 全球游戏引擎市场占有率 由于体量庞大,Unity游戏已成为受游戏黑灰产攻击的重灾区,因游…...

使用 yarn 的时候,遇到 Error [ERR_REQUIRE_ESM]: require() of ES Module 怎么解决?
晚上回到家,我打开自己的项目,执行: cd HexoPress git pull --rebase yarn install yarn dev拉取在公司 push 的代码,然后更新依赖,最后开始今晚的开发时候,意外发生了,竟然报错了,…...

多维时序 | Matlab实现基于VMD-DBO-BiLSTM、VMD-BiLSTM、BiLSTM的多变量时间序列预测
多维时序 | Matlab实现基于VMD-DBO-BiLSTM、VMD-BiLSTM、BiLSTM的多变量时间序列预测 目录 多维时序 | Matlab实现基于VMD-DBO-BiLSTM、VMD-BiLSTM、BiLSTM的多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现基于VMD-DBO-BiLSTM、VMD-BiLSTM、…...

实战营第四节笔记
这节课包含四大部分,为finetune简介、xtuner介绍、使用8GB玩转LLM和动手实践环节。 LoRA和QLoRA是两种很重要的方法,对微调模型、减少内存使用非常有效。 后面是XTuner的介绍。 之后是动手实践。可参考https://github.com/InternLM/tutorial/blob/ma…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
