数据结构与算法之堆排序
目录
- 堆排序概述
- 代码实现
- 时间复杂度
堆排序概述
堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
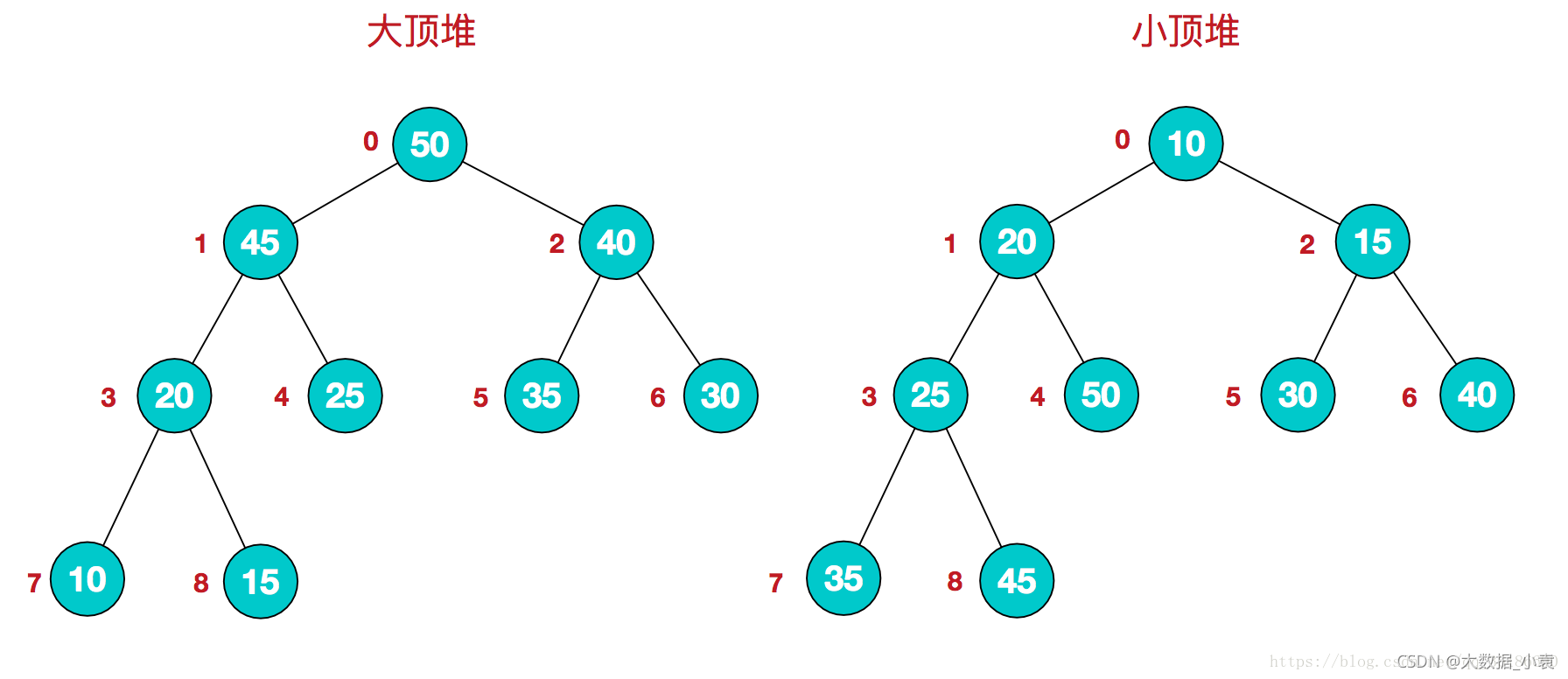 同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
 该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
-
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
-
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)
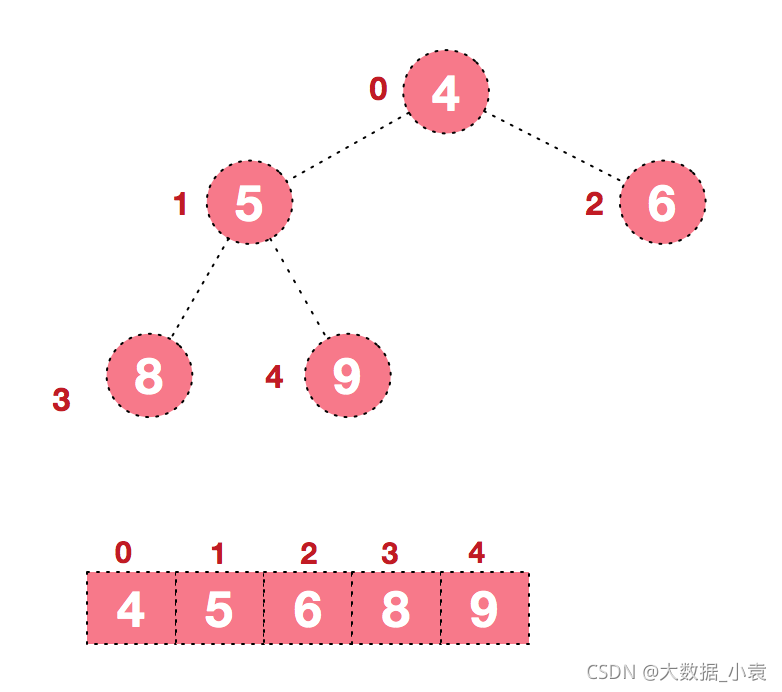
1)假设给定无序序列结构如下
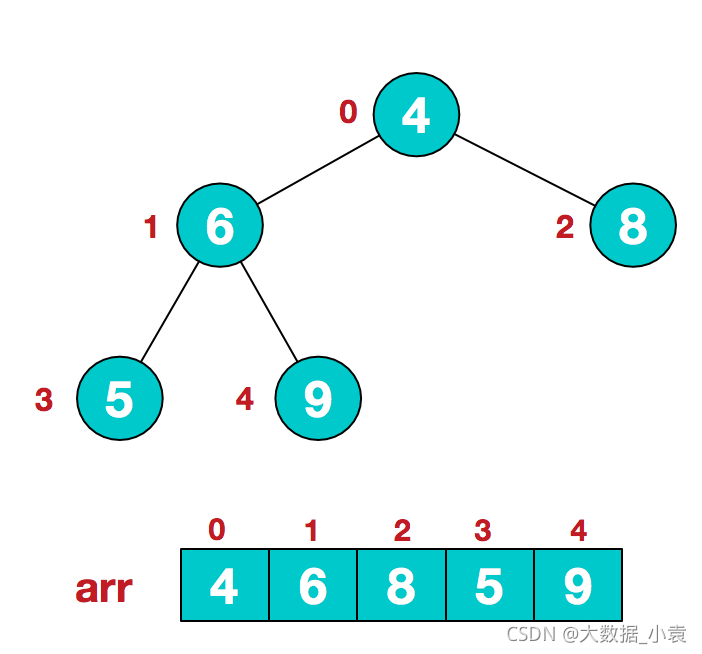
2)此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整
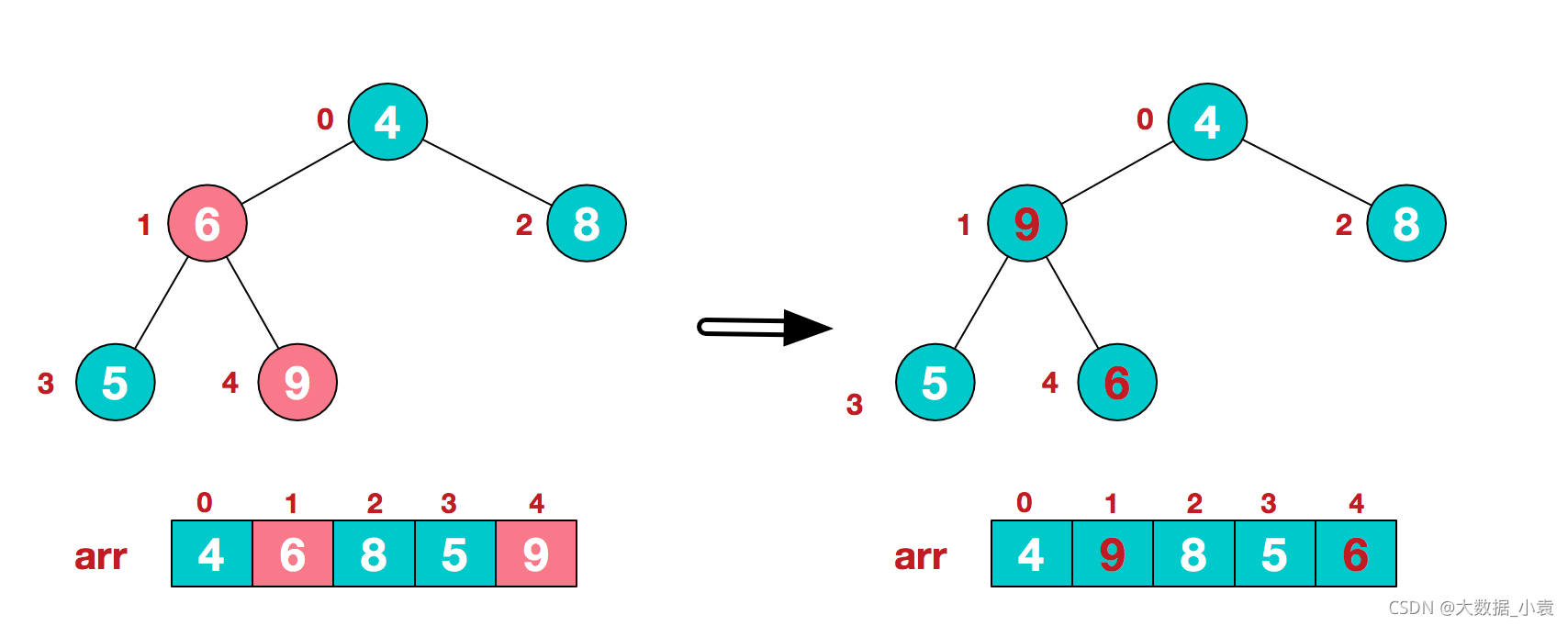
3)找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换
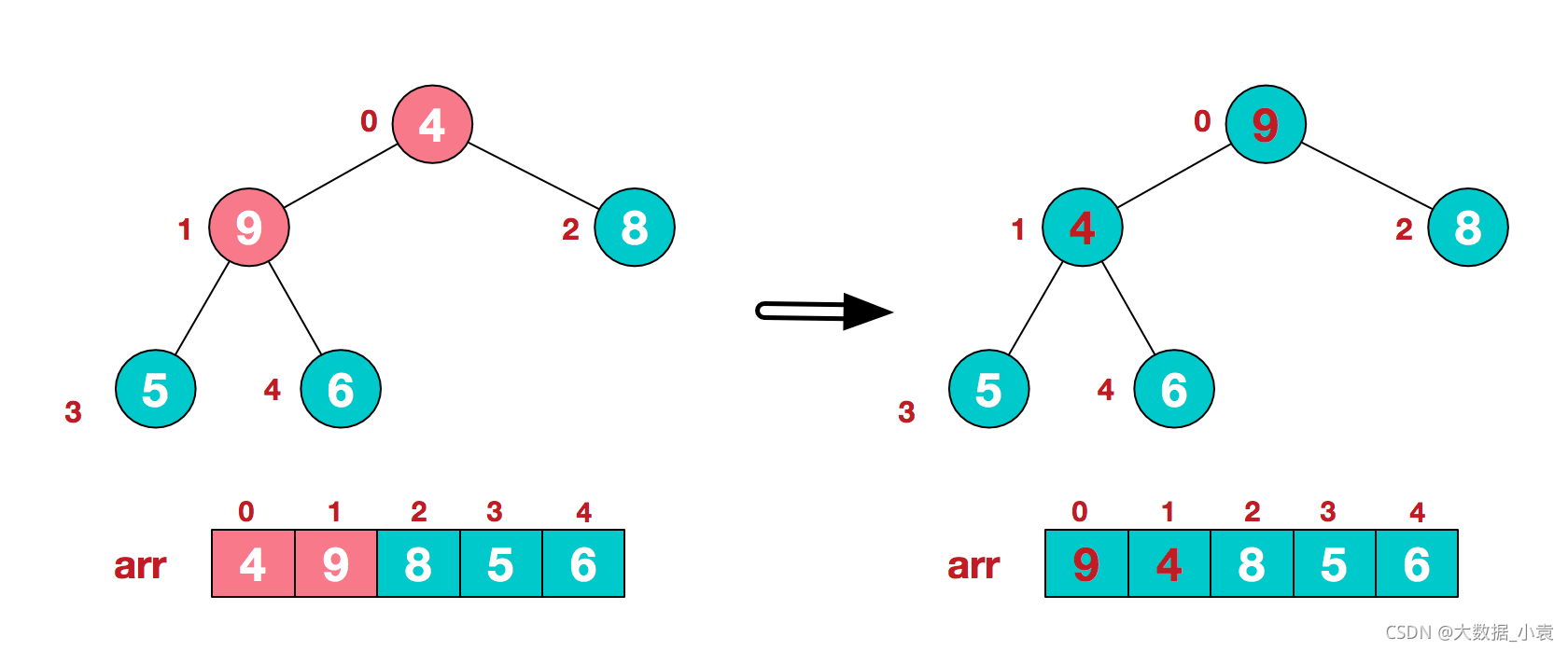 4)这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
4)这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
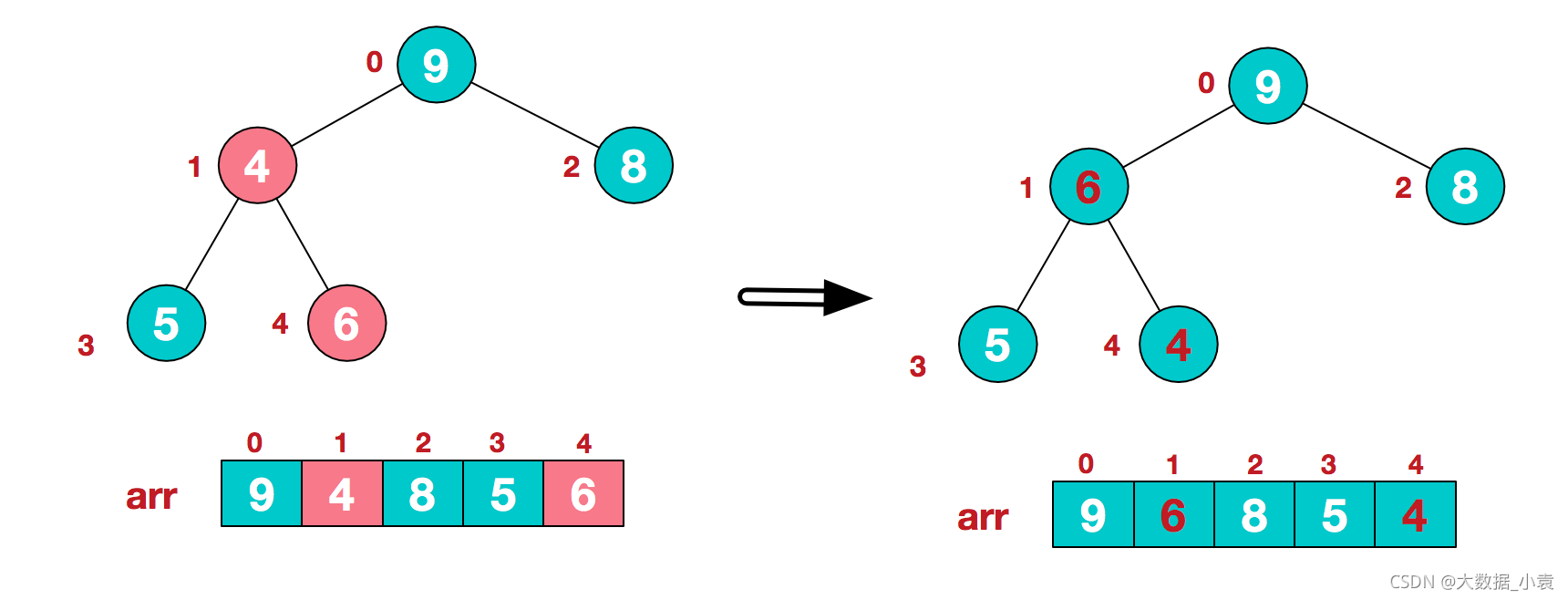 此时,我们就将一个无需序列构造成了一个大顶堆
此时,我们就将一个无需序列构造成了一个大顶堆
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换
1)将堆顶元素9和末尾元素4进行交换,9就不用继续排序了
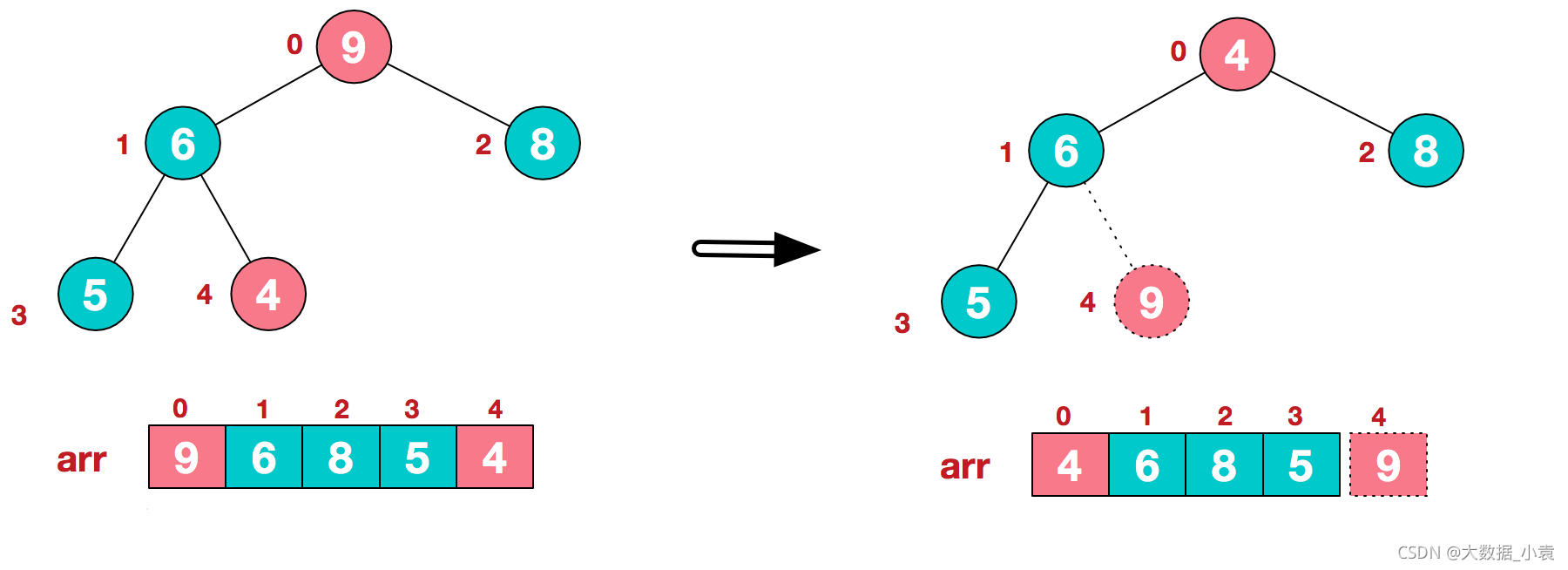
2)重新调整结构,使其继续构建大顶堆(9除外)
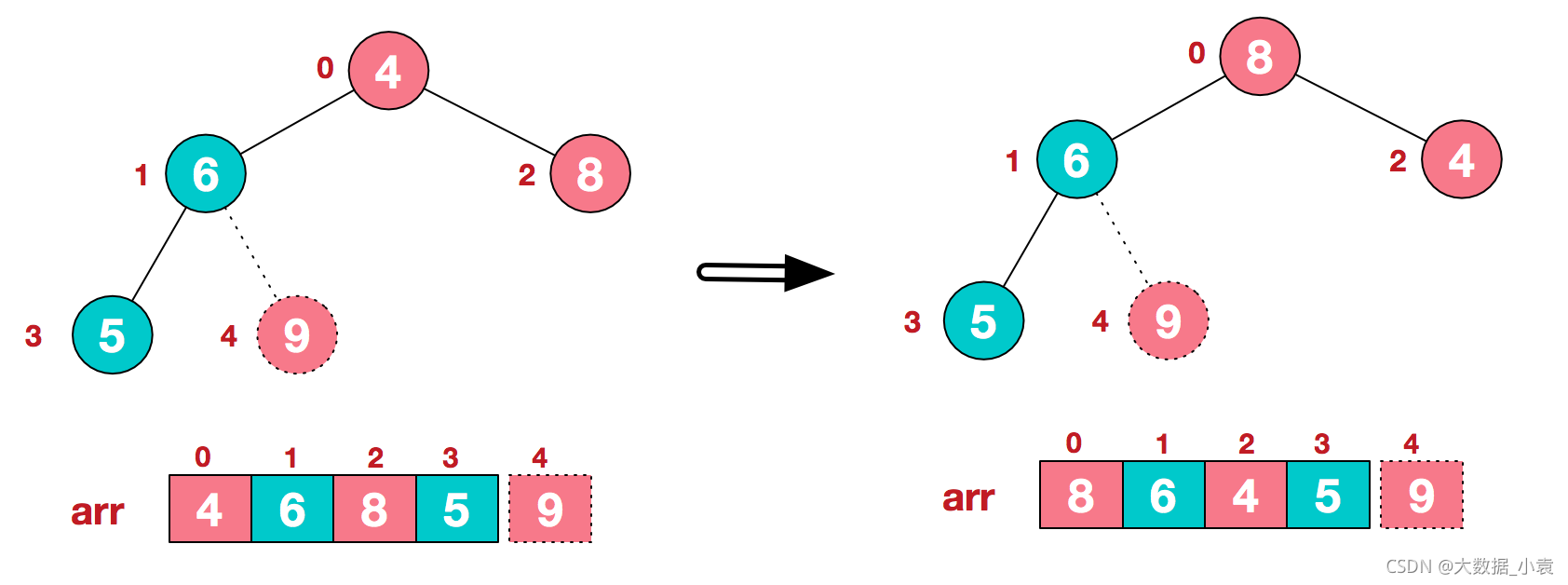
3)再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
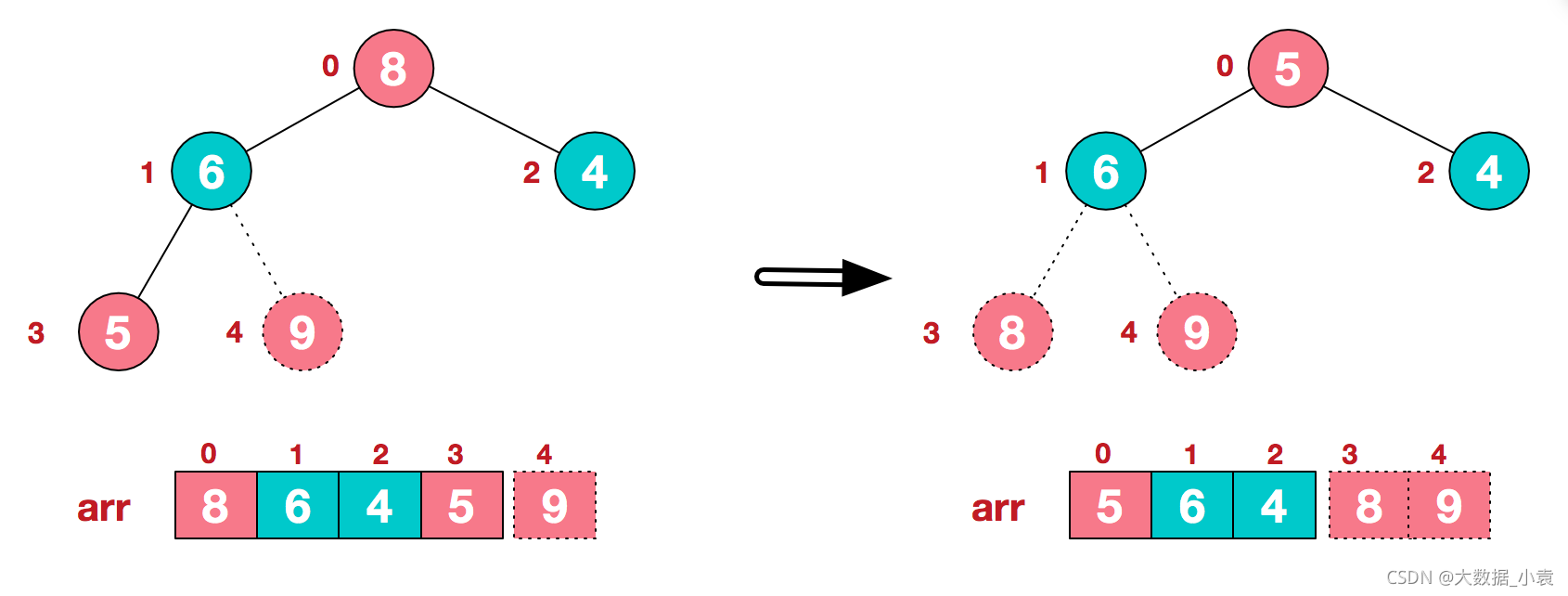
步骤三 后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
排序思路:
-
将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
-
将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
-
重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
动图展示:

代码实现
import java.util.Arrays;public class HeapSort {public static void main(String[] args) {int[] arr = {4, 6, 8, 5, 9};heapSort(arr);
// [4, 6, 8, 5, 9]
// [4, 9, 8, 5, 6]
// [4, 9, 8, 5, 6]
// [9, 6, 8, 5, 4]
// [9, 6, 8, 5, 4]
// [9, 6, 8, 5, 4]
// [8, 6, 4, 5, 9]
// [8, 6, 4, 5, 9]
// [6, 5, 4, 8, 9]
// [6, 5, 4, 8, 9]
// [5, 4, 6, 8, 9]
// [5, 4, 6, 8, 9]
// [4, 5, 6, 8, 9]}//堆排序public static void heapSort(int[] arr) {//开始位置是最后一个非叶子节点(最后一个节点的父节点)int start = (arr.length - 1) / 2;//循环调整为大顶堆for (int i = start; i >= 0; i--) {maxHeap(arr, arr.length, i);}//先把数组中第0个和堆中最后一个交换位置for (int i = arr.length - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;//再把前面的处理为大顶堆maxHeap(arr, i, 0);}}//数组转大顶堆,size:调整多少(从最后一个向前减),index:调整哪一个(最后一个非叶子节点)public static void maxHeap(int[] arr, int size, int index) {//左子节点int leftNode = 2 * index + 1;//右子节点int rightNode = 2 * index + 2;//先设当前为最大节点int max = index;//和两个子节点分别对比,找出最大的节点if (leftNode < size && arr[leftNode] > arr[max]) {max = leftNode;}if (rightNode < size && arr[rightNode] > arr[max]) {max = rightNode;}//交换位置if (max != index) {int temp = arr[index];arr[index] = arr[max];arr[max] = temp;//交换位置后,可能会破坏之前排好的堆,所以之间排好的堆需要重新调整maxHeap(arr, size, max);}//打印每次排序后的结果System.out.println(Arrays.toString(arr));}
}
时间复杂度
- 最优时间复杂度:
o(nlogn) - 最坏时间复杂度:
o(nlogn) - 稳定性:不稳定
它的运行时间主要是消耗在初始构建堆和在重建堆时的反复筛选上。
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次取堆顶记录重建堆需要用O(logi)的时间(完全二叉树的某个结点到根结点的距离为log2i+1),并且需要取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。
所以总体来说,堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n2)的时间复杂度了。
空间复杂度上,它只有一个用来交换的暂存单元,也非常的不错。不过由于记录的比较与交换是跳跃式进行,因此堆排序是一种不稳定的排序方法。
相关文章:

数据结构与算法之堆排序
目录堆排序概述代码实现时间复杂度堆排序概述 堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点…...

Vue3 中的模板语法
目录前言一、什么是模板语法?二、内容渲染指令1. v-text2. {{ }} 插值表达式3. v-html三、双向绑定指令1. v-model2. v-model的修饰符四、属性绑定指令1. 动态绑定多个属性值2. 绑定class和style属性五、条件渲染指令1. v-if、v-else-if、v-else2. v-show3. v-if和v…...

Redis十大类型——Hash常见操作
Redis十大类型——Hash常见操作命令操作简列存放及获取获取健值对长度元素查找列出健值对对数字进行操作赋值hsetnx很明显咯它也是以健值对方式存在的,只不过value也就是值,在这里也变成了一组简直对。 🍊个🌰: 想必多…...

Python采集本地二手房,一键知晓上万房源信息
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 所以今天教大家用Python来采集本地房源数据,帮助大家筛选好房。 话不多说,让我们开始愉快的旅程吧~ 更多精彩内容、资源皆可点击文章下方名片获取此处跳转 本文涉及知识点 采集基本流程 requests 发送…...

Ubuntu 18.04 出现GLIBC_2.28 not found的解决方法(亲测有效)
关于/lib/x86_64-linux-gnu/libc.so.6: version GLIBC_2.28’ not found出现报错,建议不要使用源码包去编译并升级。在下文有分享一个使用官方的Debian软件包去升级使用的方法。仅供参考! 环境 # uname -a Linux Ubuntu 5.4.0-144-generic #161~18.04.…...

Java文档搜索引擎总结
Java文档搜索引擎总结项目介绍项目使用的技术栈前端页面展示后端逻辑部分索引部分搜索模块部分Web模块部分项目介绍 Java文档搜索引擎项目是一个SSM项目,该项目的前端界面部分是由搜索页面和展示页面组成,后端部分索引模块(ScanAnalysis、in…...
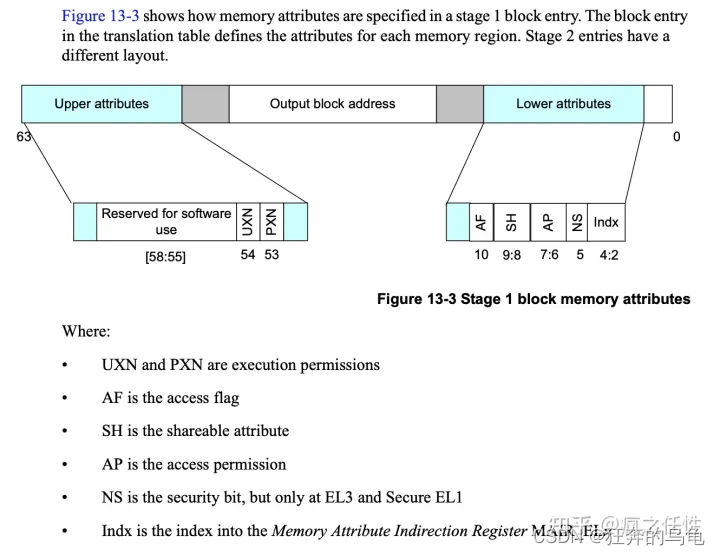
Linux内核学习笔记——页表的那些事。
目录页表什么时候创建内核页表变化什么时候更新到用户页表源码分析常见问题解答问题一:页表到底是保存在内核空间中还是用户空间中?问题2:页表访问,软件是不是会频繁陷入内核?问题3:内存申请,软…...

C++,Qt分别读写xml文件
XML语法 第一行是XML文档声明,<>内的代表是元素,基本语法如以下所示。C常见的是使用tiny库读写,Qt使用自带的库读写; <?xml version"1.0" encoding"utf-8" standalone"yes" ?> <根元素>…...
WebStorm安装教程【2023年最新版图解】一文教会你安装
文章目录引言一、下载WebStorm三、WebStorm激活配置及创建项目Active Code安装完成尝试新建一个项目引言 今天发现了一个专注前端开发的软件,相比VSCode的话,这个好像也不错,为了后续做个API接口项目做准备。 对于入门JavaScript 开发的者&am…...

用户态和内核态,系统调用
特权指令:具有特殊权限的指令,比如清内存,重置时钟,分配系统资源,修改用户的访问权限 由于这类指令的权限最大,所以使用不当会导致整个系统崩溃 系统调用:是操作系统提供给应用程序的接口(供应…...

Java 包装类
Java 中有些类只能操作对象,因此 Java 的基本数据类型都有一个对应的包装类。 byte:Byteshort:Shortint:Integerlong:Longfloat:Floatdouble:Doublechar:Characterbooleanÿ…...

Raspberry Pi GPIO入门指南
如果您想使用 Raspberry Pi 进行数字输入/输出操作,那么您需要使用 GPIO(通用输入/输出)引脚。在这篇文章中,我们将为您提供 Raspberry Pi GPIO 的基础知识,包括如何访问和操作 GPIO 引脚。 0.认识GPIO 树莓派上的那…...

汇编语言程序设计(三)之汇编程序
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编程序 经过上述课程的学习,我们可以编写一个完整的程序了。这章开始我们将开始编写完整的汇编语言程序,用编译和连接程序将它们连接成可…...

用二极管和电容过滤电源波动,实现简单的稳压 - 小水泵升压改装方案
简而言之,就是类似采样保持电路,当电源电压因为电机启动而骤降时,用二极管避免电容电压跟着降低,从而让电容上连接的低功耗芯片有一个比较稳定的供电电压。没什么特别的用处,省个LDO 吧,电压跌幅太大的时候…...

【数据结构与算法】数据结构有哪些?算法有哪些?
1. 算法与数据结构总览图 2.常用的数据结构 2.1.数组(Array) 数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地组织在一起的集合。数组可以说是最基本的数据结构,在各种编程语言中都有对应。一个数组可以分解为多个数…...
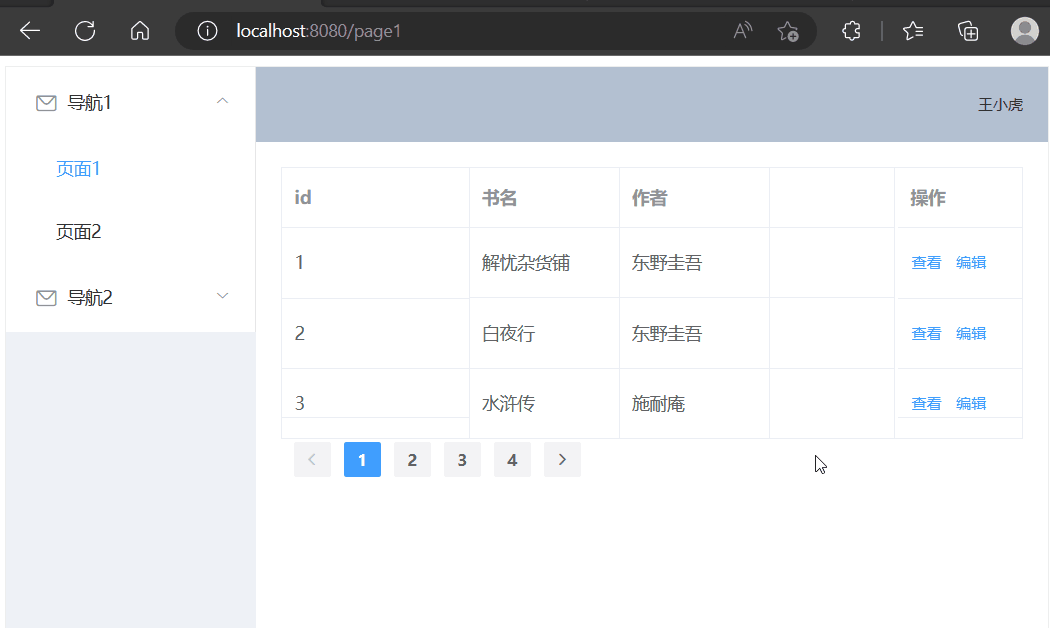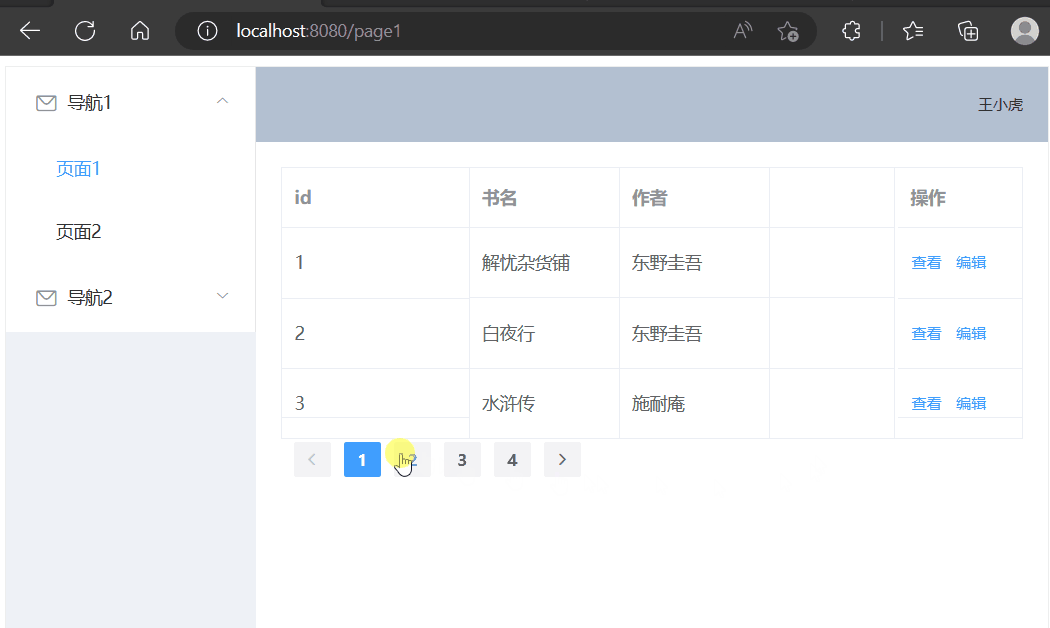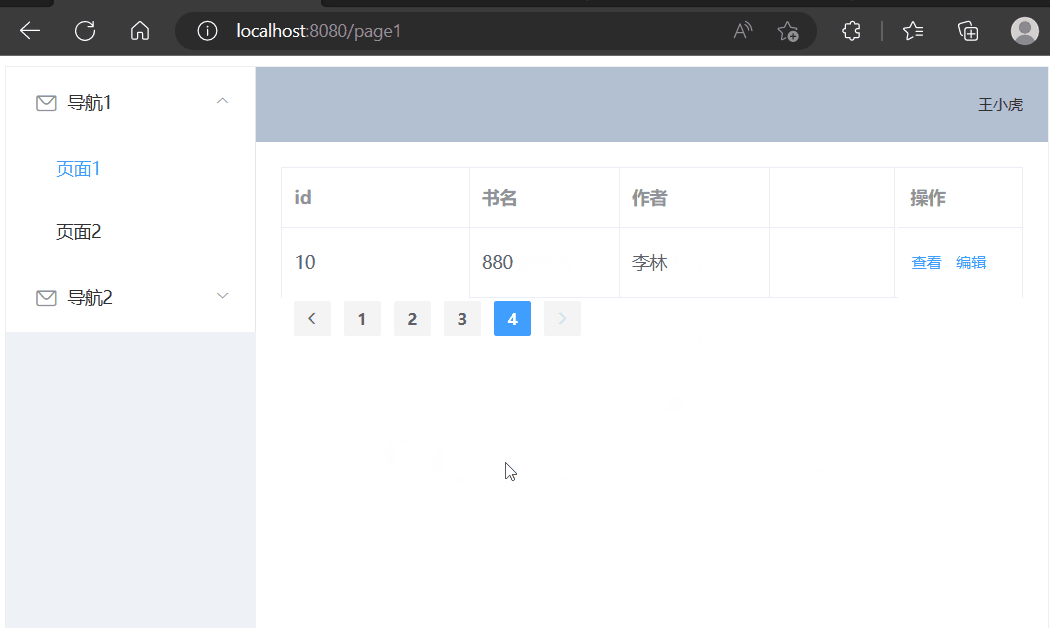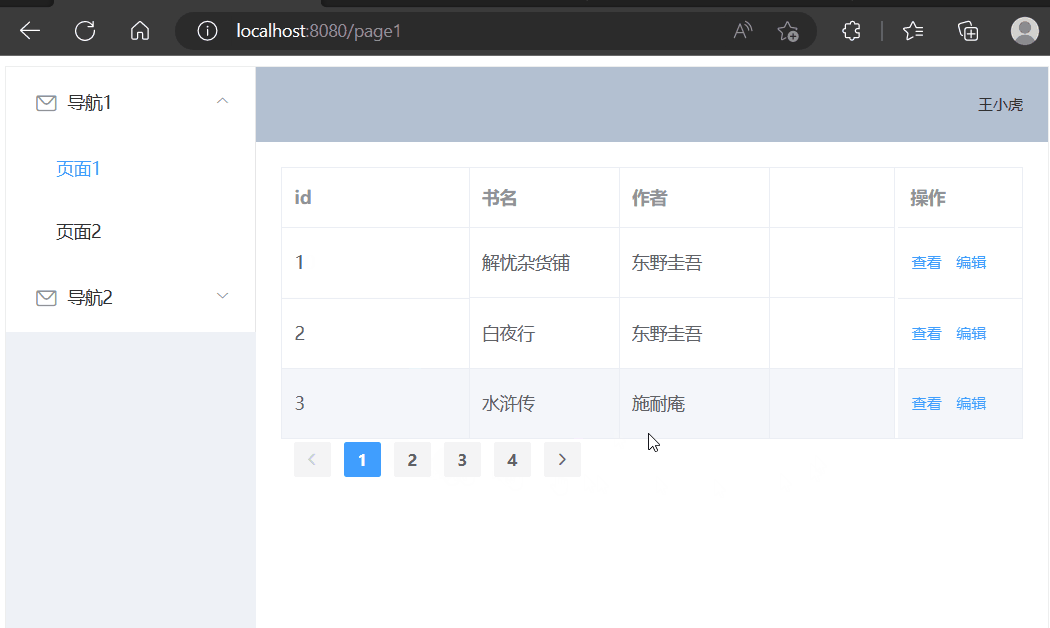
使用Element-UI展示数据(动态查询)
学习内容来源:视频P4 本篇文章进度接着之前的文章进行续写 精简前后端分离项目搭建 Vue基础容器使用 目录选择组件修改表格组件修改分页组件增加后端接口前端请求数据接口页面初始化请求数据点击页码请求数据选择组件 在官方文档中选择现成的组件,放在页…...

lamda 表达式例子全集
1、List 转 map 1.1、key(Model属性) value Model Map<String, Model> modeMap List.stream().collect(Collectors.toMap(Model1::属性get方法, v -> v, (p1, p2) -> p1)); 1.2、key(Model1属性) value Model2 Map<String, Model1> model2Map List.stream…...

计算机网络第八版——第一章课后题答案(超详细)
第一章 该答案为博主在网络上整理,排版不易,希望大家多多点赞支持。后续将会持续更新(可以给博主点个关注~ 【1-01】计算机网络可以向用户提供哪些服务? 解答:这道题没有现成的标准答案,因为可以从不同的…...
嵌入式和Python(二):python初识及其基本使用规则
目录 一,python基本特点 二,python使用说明 ● 两种编程方式 ① 交互式编程 ② 脚本式编程 ● python中文编码 ● python行和缩进 ● python引号 ● python空行 ● python等待用户输入 ① 没有转换变量类型 ② 转换变量类型 ● python变…...

C语言详解双向链表的基本操作
目录 双链表的定义与接口函数 定义双链表 接口函数 详解接口函数的实现 创建新节点(BuyLTNode) 初始化双链表(ListInit) 双向链表打印(ListPrint) 双链表查找(ListFind) 双链…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
