B树的介绍
R-B Tree
- 简介
- 特性
- B树
- 特性
- m阶B树的性质(这些性质是B树规定的)
- B树的搜索
- B树的添加
- B树的删除——非叶子结点
简介
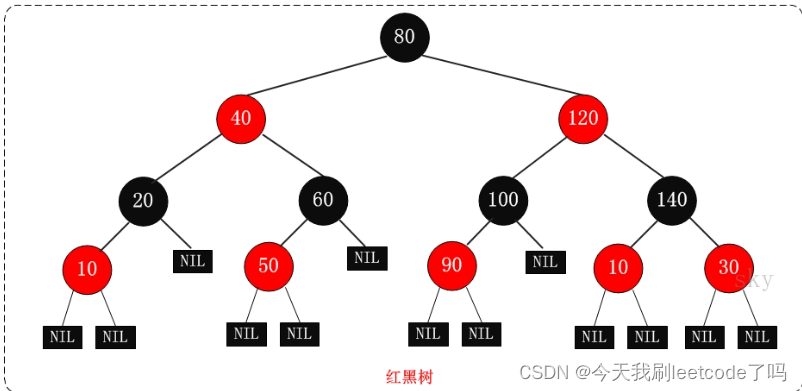
R-B Tree又称为Red-Black Tree,红黑树。是一种特殊的二叉查找树,红黑树的每个节点上都有存储为表示结点的颜色,可以是红或者黑色。
特性
- 每个结点或者是黑色或者红色
- 根结点是黑色
- 每个叶子节点是黑色(这里的叶子结点指的是:NULL的叶子结点——外部节点 (写代码时候不用加入这些结点))
- 如果一个节点红色的,则它的子结点黑色的
- 结点红色的,则它的父结点黑色的(否则:如果父结点是红色,那么不满足上一条性质 如果该节点是红色的,那么它的子结点是黑色的这个性质了)
- 从根结点到叶子结点(外部节点)的所有路径上不能包含两个连续的红结点
- 从任意节点到叶子结点的所有路径都包含相同数量的黑节点
特性5说明:确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
这样使得在叶子结点中原来的度为0或者度为1的结点最后全部变成了度为2的结点
B树
B树是一种平衡的多路搜索树
特性
- B树的一个节点可以存储超过两个元素,可以拥有超过两个子结点
- 平衡,每个结点的所有子树高度一致
- B树 比较矮
m阶B树的性质(这些性质是B树规定的)
可以理解为一个节点最多拥有的子结点数目(3阶B树:代表一个结点最多含有3个子结点)
m阶B树:代表一个结点最多包含5个子结点
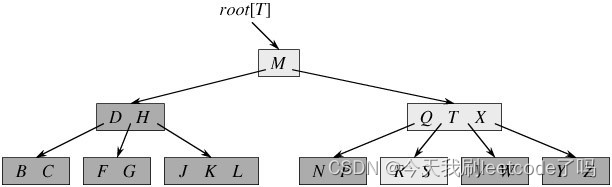
下图所示的B树:最多的结点是(包含元素QTX结点,最多包含了4个结点——称为4阶B树)
前提:假设一个节点存储的元素个数为X,
- 那么其根结点:1≤X≤m-1(当X=m-1时候才会存在m个根结点)
- 那么对于非根结点:┌m/2┐-1≤X≤m-1()
- 一个节点它的子结点的个数等于这个结点的元素个数+1:子结点的个数为y=x+1
4 那么非根结点的个数:为非根结点的元素左右加一:┌m/2┐≤y≤m
例如:8阶B树,其子结点的个数≤8, m=8, ┌m/2┐ = 4, 4≤y≤8, 3≤X≤7,则8阶B树可以称为(4,8)树;4-8树- 非根结点:┌m/2┐(┌m┐表示对m向上取整)-1≤X≤m-1
思考为什么非根结点必须满足┌m/2┐-1的向上取整的性质
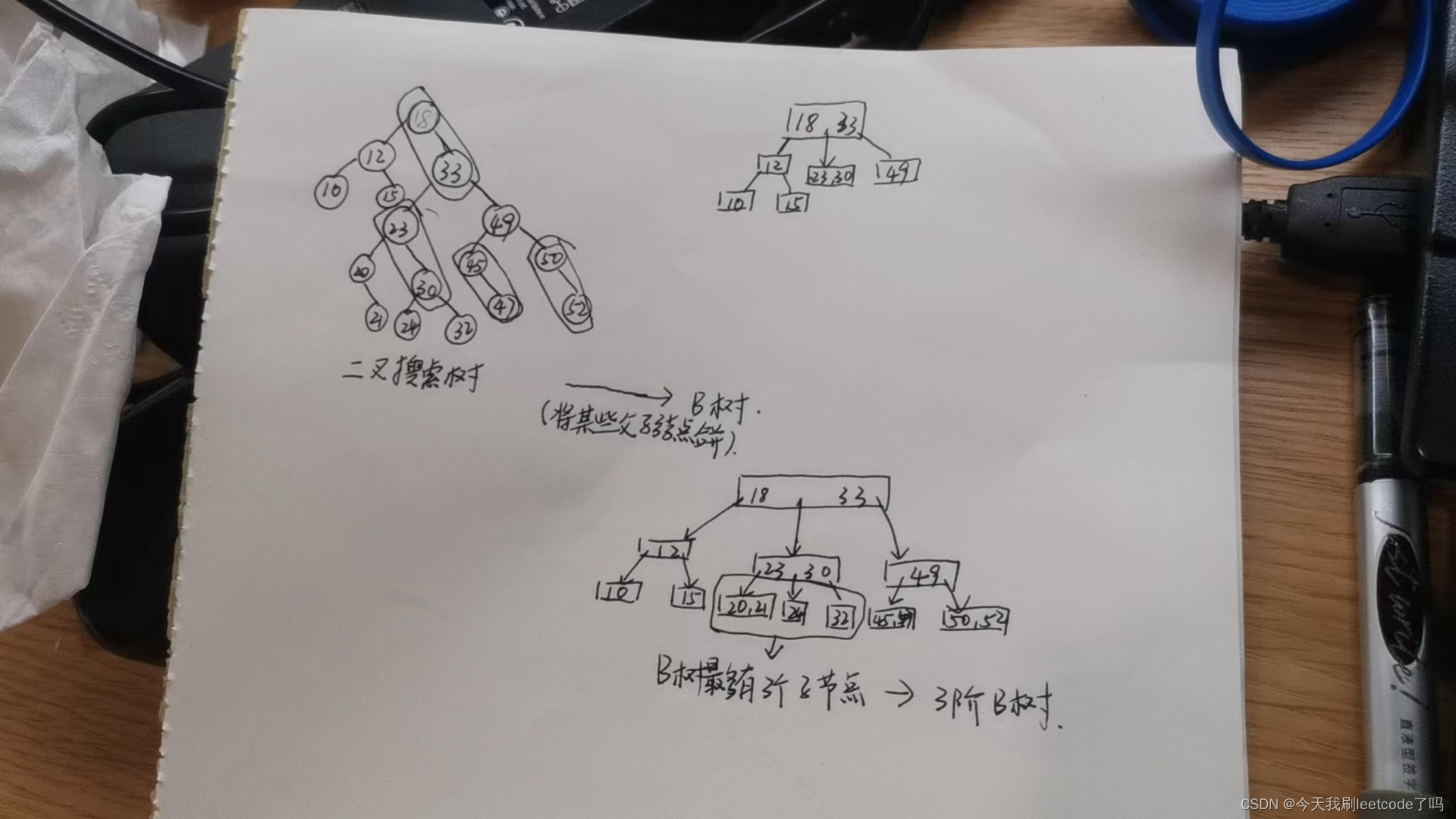
B树与二叉搜索树具有等价性:
二叉搜索树的多代结点合并可以获得一个超级结点(存储多个元素)
两代合并的超级结点首先满足如果根结点存在子结点,那么子结点的数目是根结点的数目+1===>y = x+1最多含有四个子结点
三代合并的超级结点(那么合并的超级结点 其存在的元素个数最多是将3代中的七个结点 合并在一个结点中,最终形成了具有7个元素的超级结点,那么最终其子节点的个数最多有8个(8阶B树))
n代合并的超级结点,那么最多含有2n个子结点也就是2n阶树可以理解为n代的子结点的最多个数
m阶B树,最多需要log2m代进行合并
B树的搜索
此图呈现的是4阶B树
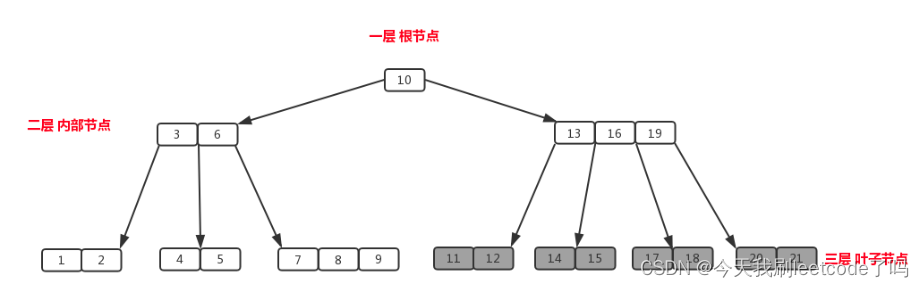
B树的搜索流程:
- 先在结点内部通过从小到大顺序来搜索元素
- 如果命中,搜索结束
- 如果未命中,再通过去对应的子结点中搜索元素,重复步骤1的操作。
B树的添加
明确:新添加的元素必定是添加到叶子结点(不断比较,直到到最后一层,进行结点的添加)
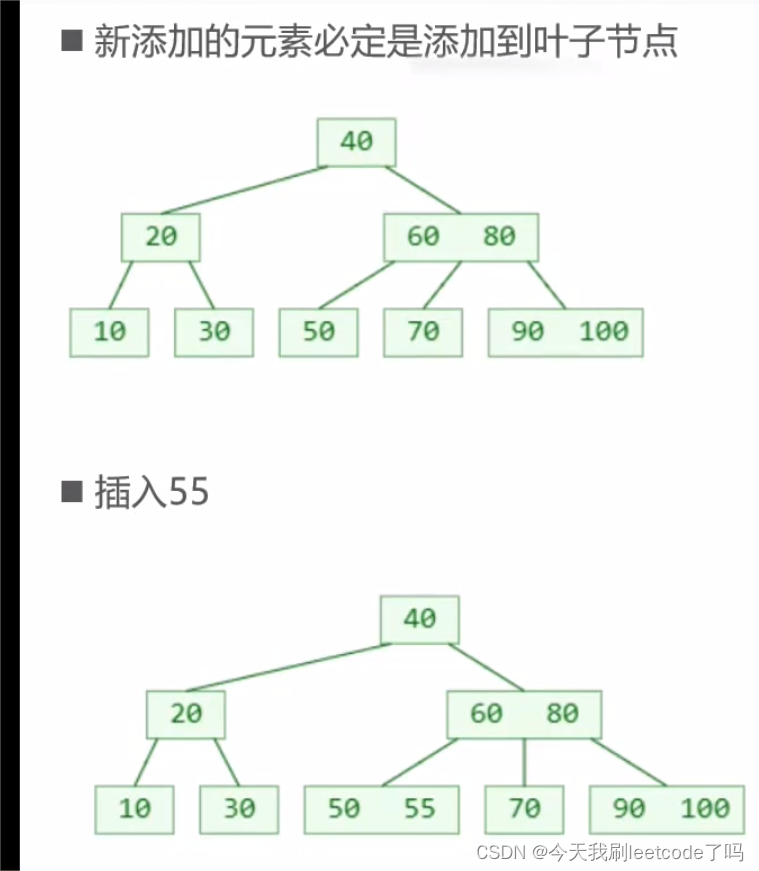
如果这个B树是3阶B树——>结点最多存储2个元素,此时如果插入98到右下角的子结点以后,出现上溢(overflow)
上溢结点的元素个数必然等于B树的阶数
求出上溢结点最中间元素的位置为K,将K位置的元素与父结点合并,再将K位置的元素向上与父结点合并
将[0,k-1]以及[k1,m-1]的位置的元素分裂成两个子结点
这两个子结点的元素的个数,必然都不会低于最低限制(┌m/2┐-1)
一次分裂完毕后,可能导致父结点上溢,依然按照上述方式解决。
最极端的情况可能是一直分裂到根结点。
B树的删除——非叶子结点
假如需要删除的元素在非叶子节点中
1)先找到前驱或者后继元素,然后使得这个直接前驱或者直接后继元素覆盖掉所要删除的元素的值
2)再把这个直接前驱或者直接后继元素删除
往往非叶子节点的前驱或者后继元素必定在叶子节点中
所以最终的删除前驱或者后继元素,就是最开始提到的情况删除的元素在叶子结点中——往往真正删除的元素都发生在叶子节点中
但是必须要满足对于非根结点,其对应的结点的个数为┌m/2┐-1但是删除后的结点可能不满足这个硬性要求(叶子节点被删掉一个元素后,元素的个数可能会低于最低限制┌m/2┐-1)。此时需要做的操作为因为下溢结点的元素数量必然满足其值等于┌m/2┐-2,所以,如果下溢结点的邻近的兄弟结点,至少有┌m/2┐个元素,那么此时产生下溢的结点可以向其兄弟节点借一个元素——将父结点的元素b插入到下溢结点的0(最小位置),然后用兄弟节点的a(最大的元素)代替父结点中的元素b——这种操作其实满足旋转
但是对于下溢结点其邻近的结点只有┌m/2┐-1个元素的情况——(也就是不能元素借位),选择把中间的父结点的元素b挪下来将左右子节点进行合并,合并后的结点的元素个数┌m/2┐+┌m/2┐-2≤m-1
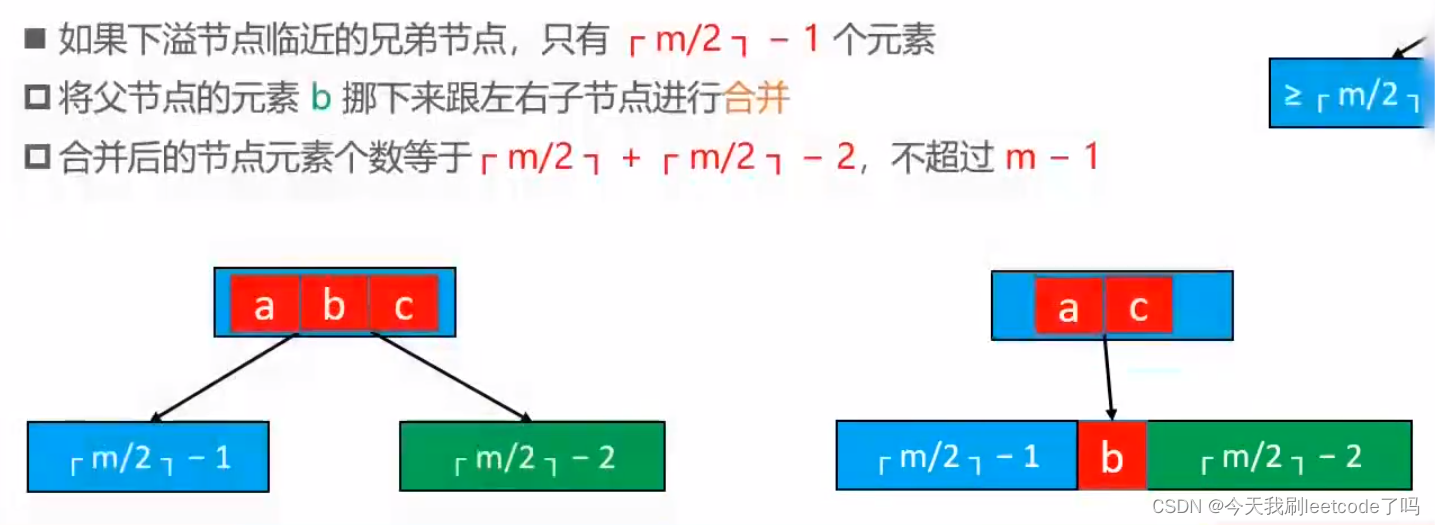
这个可能导致父结点的下溢——依然按照上述的方法解决,下溢现象可能会一直往上传播,最终传播到根结点
唯一一种能够让B树长高的情况——添加元素后,上溢一直持续到根结点
唯一一种能够让B树变矮的情况——删除元素后,下溢一直持续到根结点
同时,在下溢进行右旋转的时候,如果借的兄弟节点的右子树存在,那么这个右子树需要更改插入到已经借结点成功的结点的最左子树——因为从父结点下来的结点,肯定该元素是小于右侧子节点的最小元素值,所以插入0位置,同时原本该父结点的左子树的右子树的值也比该元素小,所以需要插入到该结点元素的最左子树位置
相关文章:

B树的介绍
R-B Tree 简介特性B树特性m阶B树的性质(这些性质是B树规定的) B树的搜索B树的添加B树的删除——非叶子结点 简介 R-B Tree又称为Red-Black Tree,红黑树。是一种特殊的二叉查找树,红黑树的每个节点上都有存储为表示结点的颜色&…...
)
《The Art of InnoDB》第二部分|第4章:深入结构-磁盘结构-撕裂的页面(doublewrite buffer)
4.5 撕裂的页面 目录 4.5 撕裂的页面 4.5.1 双写缓冲区的作用 4.5.2 双写缓冲区的结构 4.5.3 双写缓冲区与Redolog的协同工作流程 4.5.2 双写缓冲区写入时机 4.5.3 禁用双写缓冲区 4.5.4 小结 未完待续... 上文我们学习了redo log的结构和其工作原理,它是一个…...
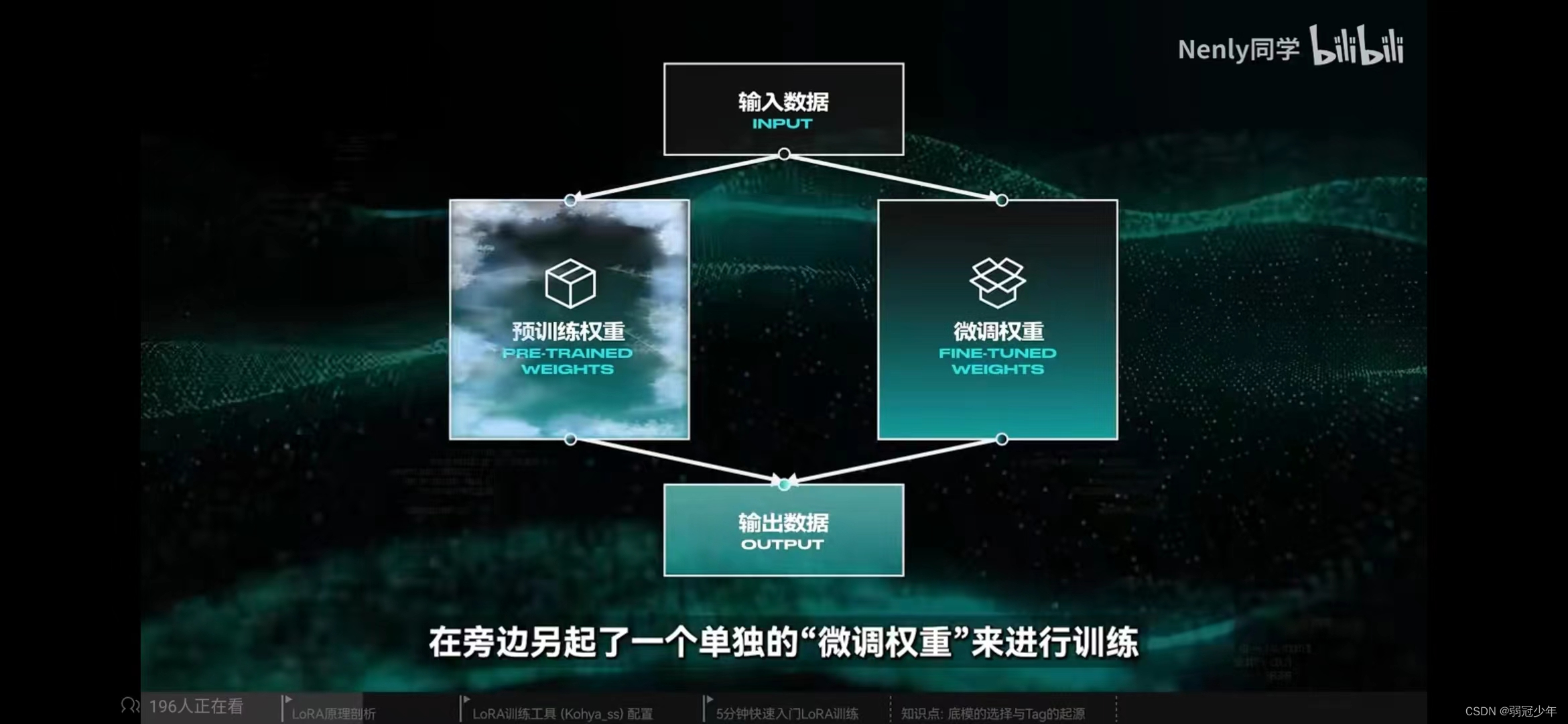
提示工程(Prompt Engineering)、微调(Fine-tuning) 和 嵌入(Embedding)
主要参考资料: 还没搞懂嵌入(Embedding)、微调(Fine-tuning)和提示工程(Prompt Engineering)?: https://blog.csdn.net/DynmicResource/article/details/133638079 B站Up主Nenly同学…...
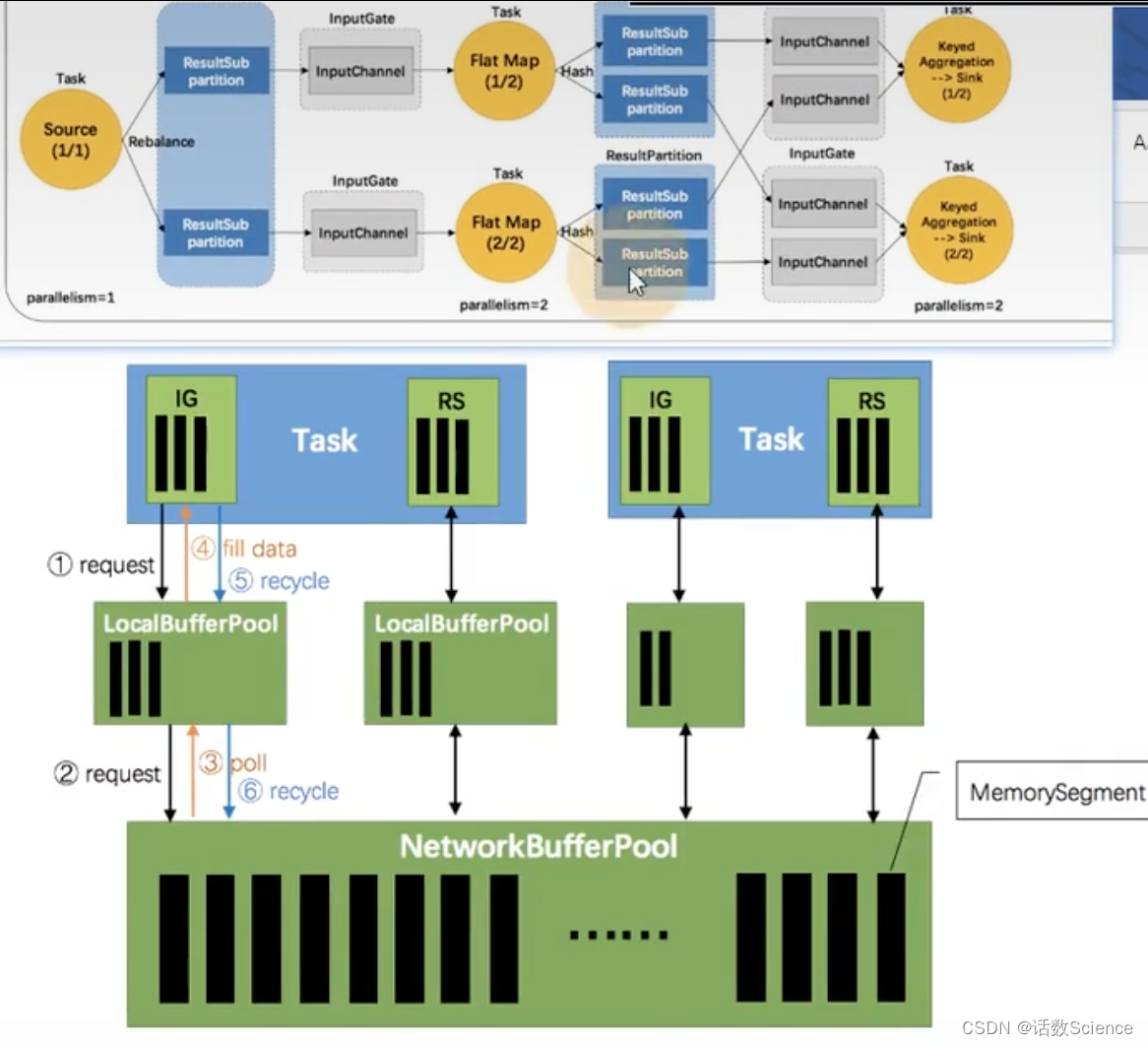
【Flink精讲】Flink 内存管理
面临的问题 目前, 大数据计算引擎主要用 Java 或是基于 JVM 的编程语言实现的,例如 Apache Hadoop、 Apache Spark、 Apache Drill、 Apache Flink 等。 Java 语言的好处在于程序员不需要太关注底层内存资源的管理,但同样会面临一个问题&…...

正则化概念及使用
正则化概念及使用 正则化概念正则化原理常用的两种正则化方法1. L1 正则化(Lasso)2. L2 正则化(Ridge) 正则化参数 正则化概念 在机器学习中,我们致力于通过从训练数据中学习模式或规律来构建模型。为了找到最佳的模型…...
让程序员设计B端界面,好比武大郎招聘:向我看齐。不忍直视!
hello,我是大美B端工场,B端系统的要求越来越高了,很多公司还让程序员负责页面,页面搞的没法看,也怪不得程序员。程序员来搞页面,那还不是武大郎招聘——向我看齐,以我的标准为标准吗?…...
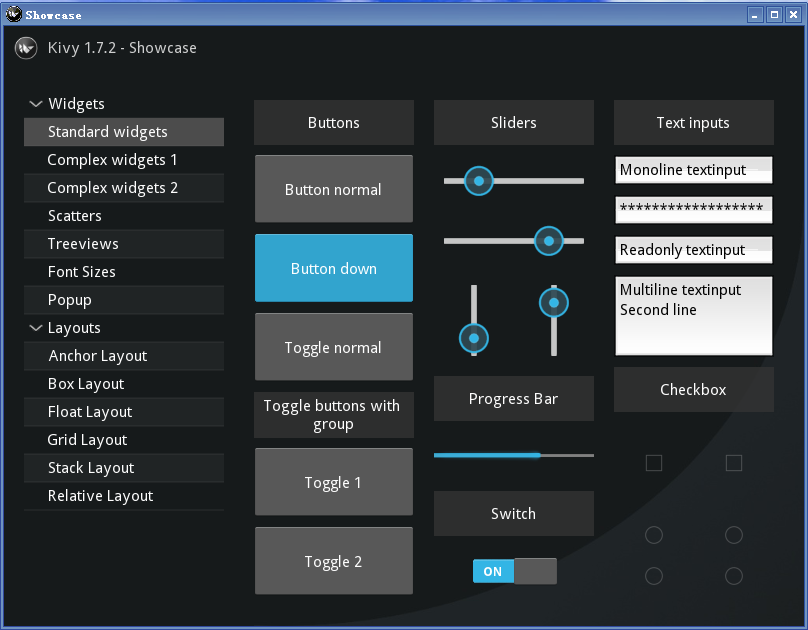
使用python构建Android,探索跨平台应用开发Kivy框架
使用python构建Android,探索跨平台应用开发Kivy框架 1. 介绍Kivy框架 Kivy是什么? Kivy是一个开源的Python跨平台应用程序开发框架,旨在帮助开发者快速构建创新的、可扩展的移动应用和多点触控应用。Kivy采用MIT许可证,允许开发…...
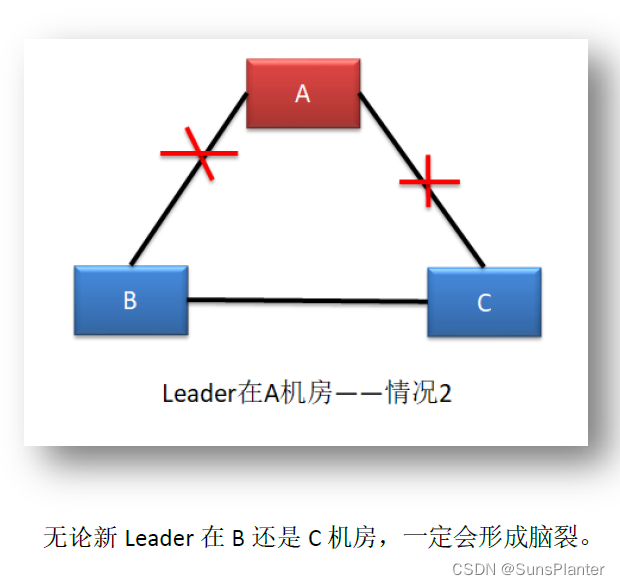
08 Redis之集群的搭建和复制原理+哨兵机制+CAP定理+Raft算法
5 Redis 集群 2.8版本之前, Redis采用主从集群模式. 实现了数据备份和读写分离 2.8版本之后, Redis采用Sentinel哨兵集群模式 , 实现了集群的高可用 5.1 主从集群搭建 首先, 基本所有系统 , “读” 的压力都大于 “写” 的压力 Redis 的主从集群是一个“一主多从”的读写分…...
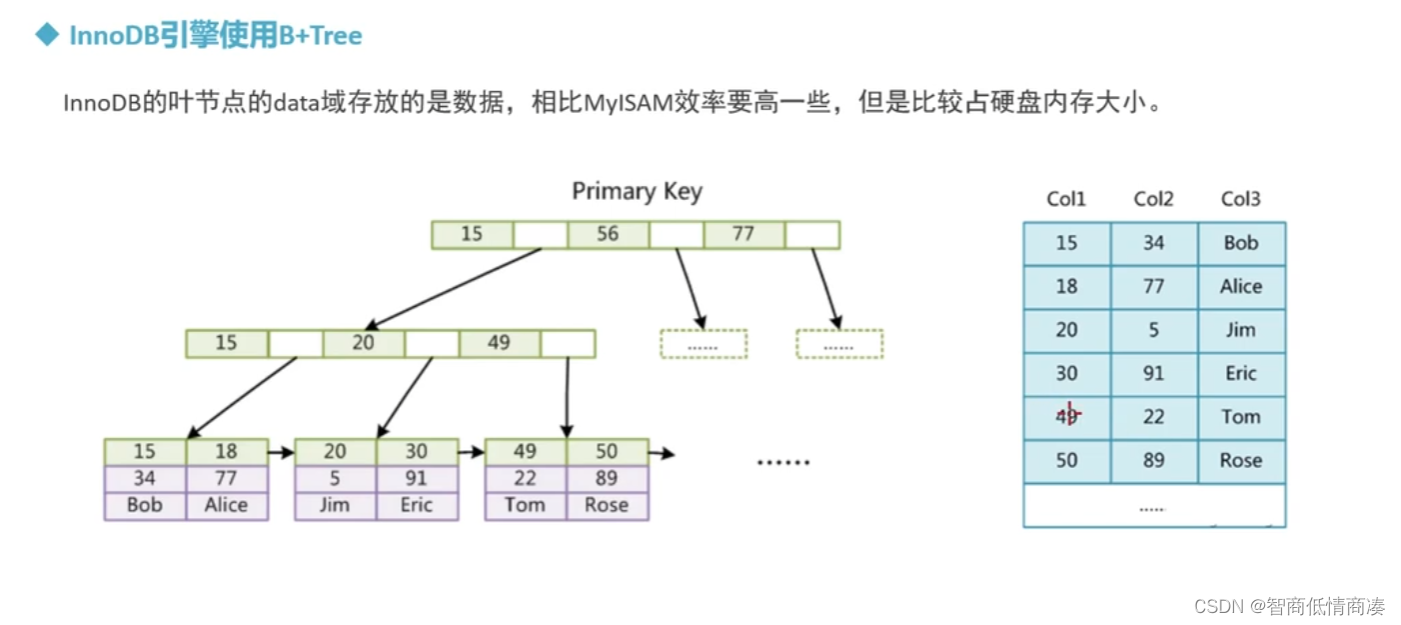
*MYSQL--索引--内部原理
MYSQL的索引根据功能,主要有三大类型: 1.HASH索引 2.二叉树 3.BTREE索引 一:HASH索引 1.内部原理: 在设置了某列为索引列之后,并且开始或者将要在相应索引列创建数据的时候,系统通过某种算法 F(X) 自动计算出来一个十六进制的哈希值,这个哈希值能够对应相应的字段值 所以…...

docker安装kafka和kafka-console-ui
3、安装kafka https://blog.csdn.net/m0_64210833/article/details/134199061 kafka依赖Zookeeper,当然也可以用内置的kraft。 安装前提条件 1.安装Zookeeper 1.1运行ZooKeeper容器 2.运行Kafka容器 2.1启动Kafka容器 3.验证 3.1进入Kafka容器 3.2查看容器状态 3.3查…...
Linux:gitlab创建组,创建用户,创建项目
创建组和项目 让后可以在组里创建一个个仓库 创建成员 我创建个成员再把他分配进这个组里 进入管理员 密码等会我们创建完用户再去配置密码 Regular是普通的用户,只可以正常去访问指定规则的项目 而下面的administrator就是管理员,可以随便进项目&…...

相机选型介绍
摄影测量中,相机是非常重要的角色,合适的相机产出合适的图像,得到合适的重建精度,这是相机的重要性。 您也许第一反应是,摄影测量所需的理想相机,是有着超高分辨率的相机,但事实可能并非如此&a…...

SQL创建数据库
SQL,全称结构化查询语言(Structured Query Language),是一种用于管理关系型数据库的标准语言。通过 SQL,我们可以创建、查询、更新和删除数据库中的数据。今天,我们将学习使用SQL创建数据库。本文的目标是让读者了解如何使用SQL创…...
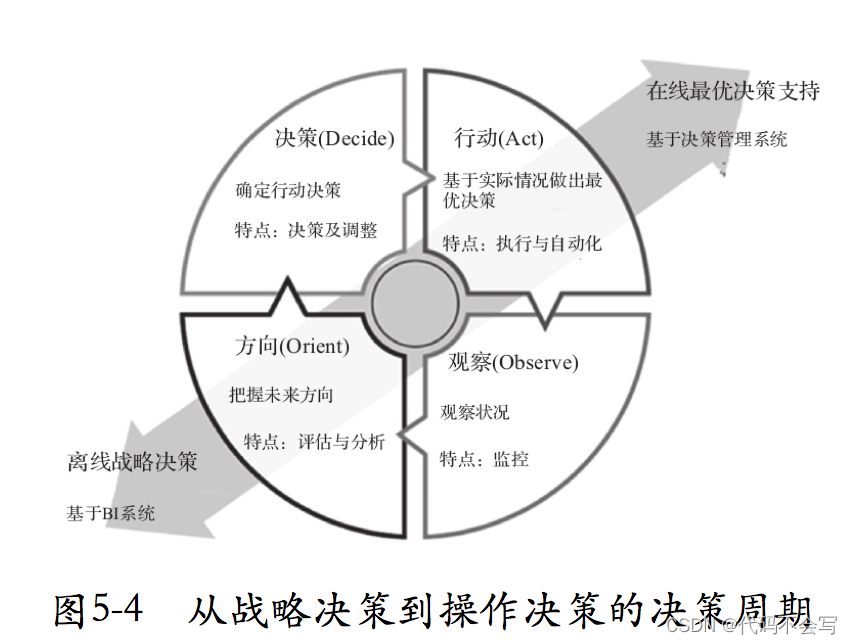
读书笔记-增强型分析:AI驱动的数据分析、业务决策与案例实践
目录 前言 运用人工智能技术,可以使人类社会变得更美好。人们总是期待产品更适合、服务更贴心、生活更便利。在实践中,技术给企业赋能,企业通过优质的产品和服务满足社会,提升人类福祉。很多金融企业已经开始尝试向潜在客户推送…...
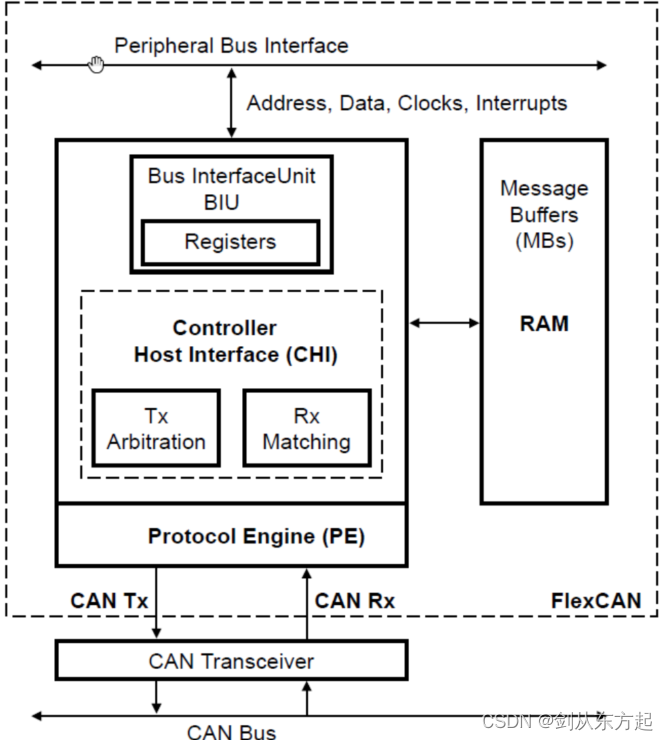
NXP实战笔记(十):S32K3xx基于RTD-SDK在S32DS上配置CAN通信
目录 1、概述 2、SDK配置 2.1、配置目标 2.2、CAN配置 3、代码实现 4、测试结果 1、概述 S32K3xx的FlexCan与之前的S32K1xx很相似,Can的中断掩码寄存器(IMASK3)与中断标志位寄存器(IFLAG3)依赖于邮箱数。 FlexCan配置实例如下 FlexCan的整体图示如下 Protocol Engine…...

纳斯达克大屏-投放需要知道的几个条件-大舍传媒
引言 随着移动互联网的快速发展,数字广告媒体广告越来越受到企业的关注。纳斯达克大屏作为全球最大的数字媒体广告投放平台之一,拥有广泛的受众和优质的媒体资源,吸引了众多企业的眼球。要想在纳斯达克大屏上投放广告,企业需要了…...
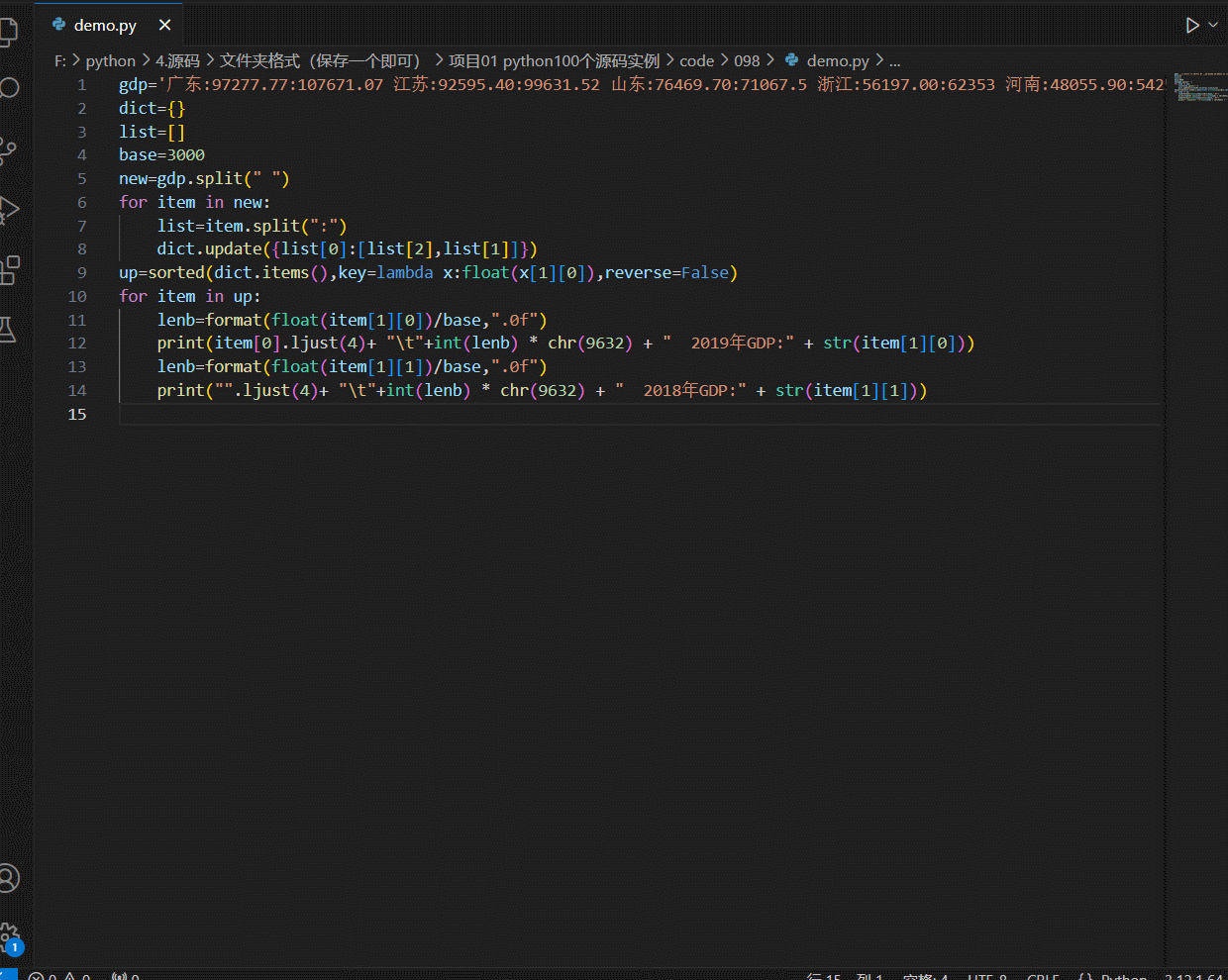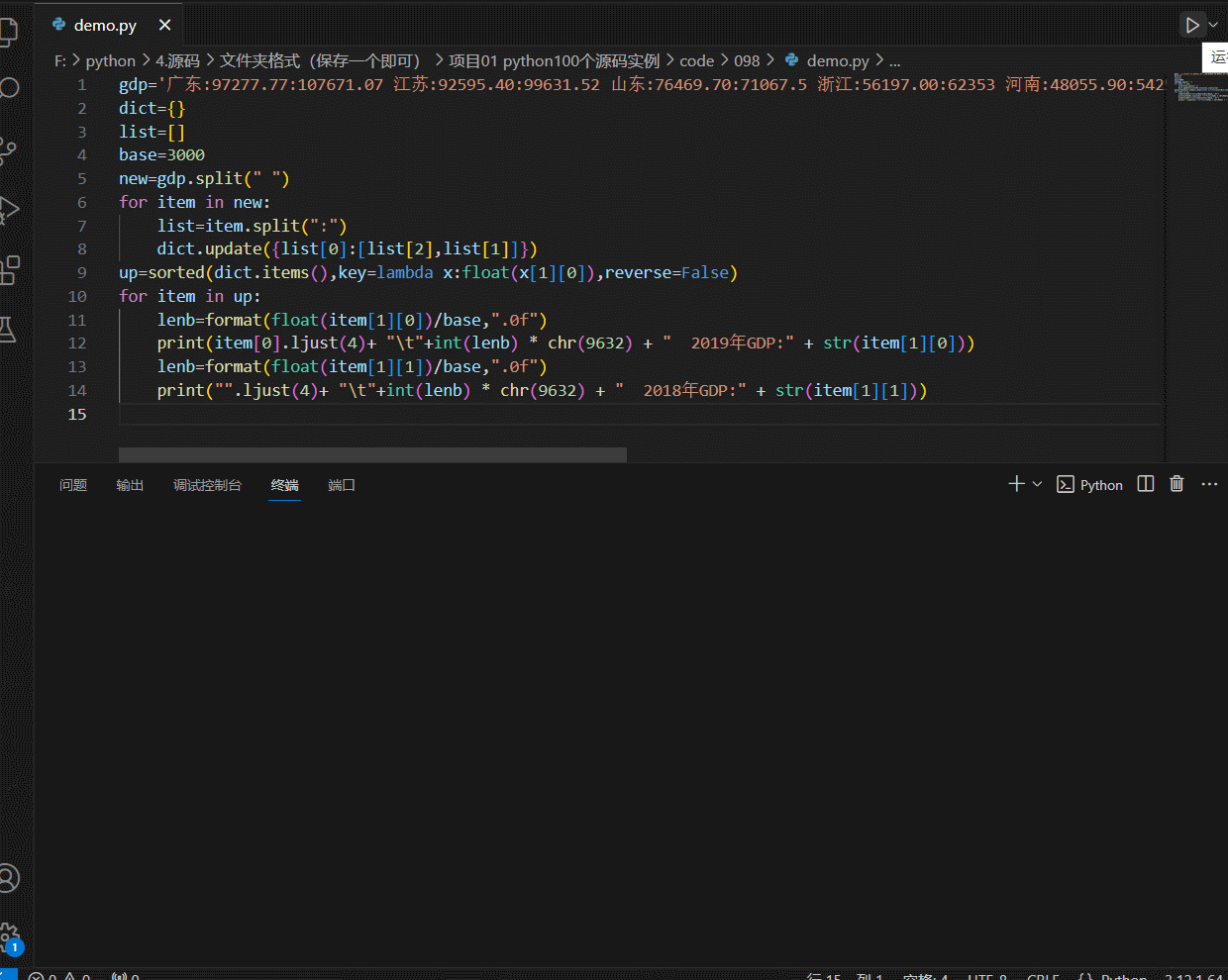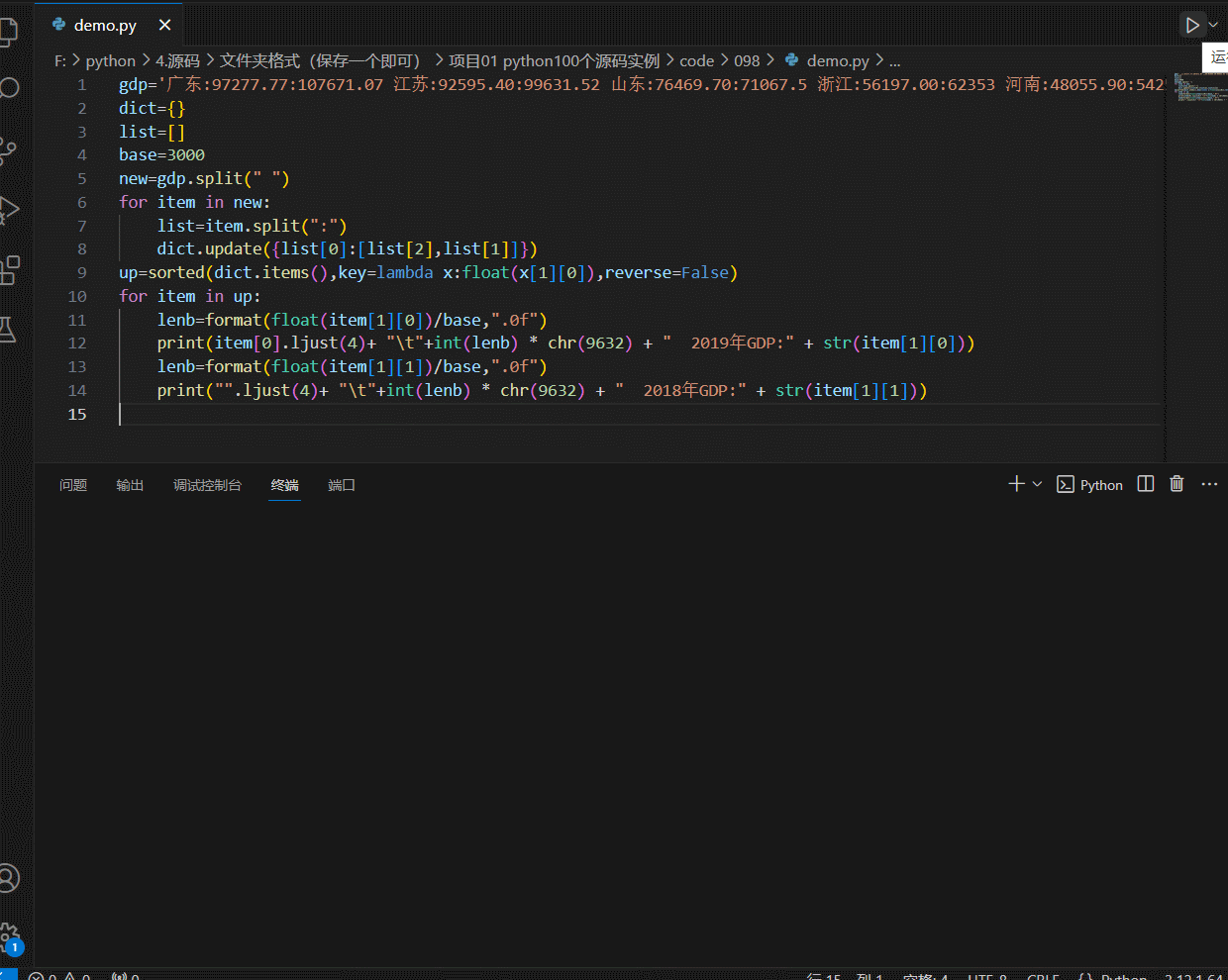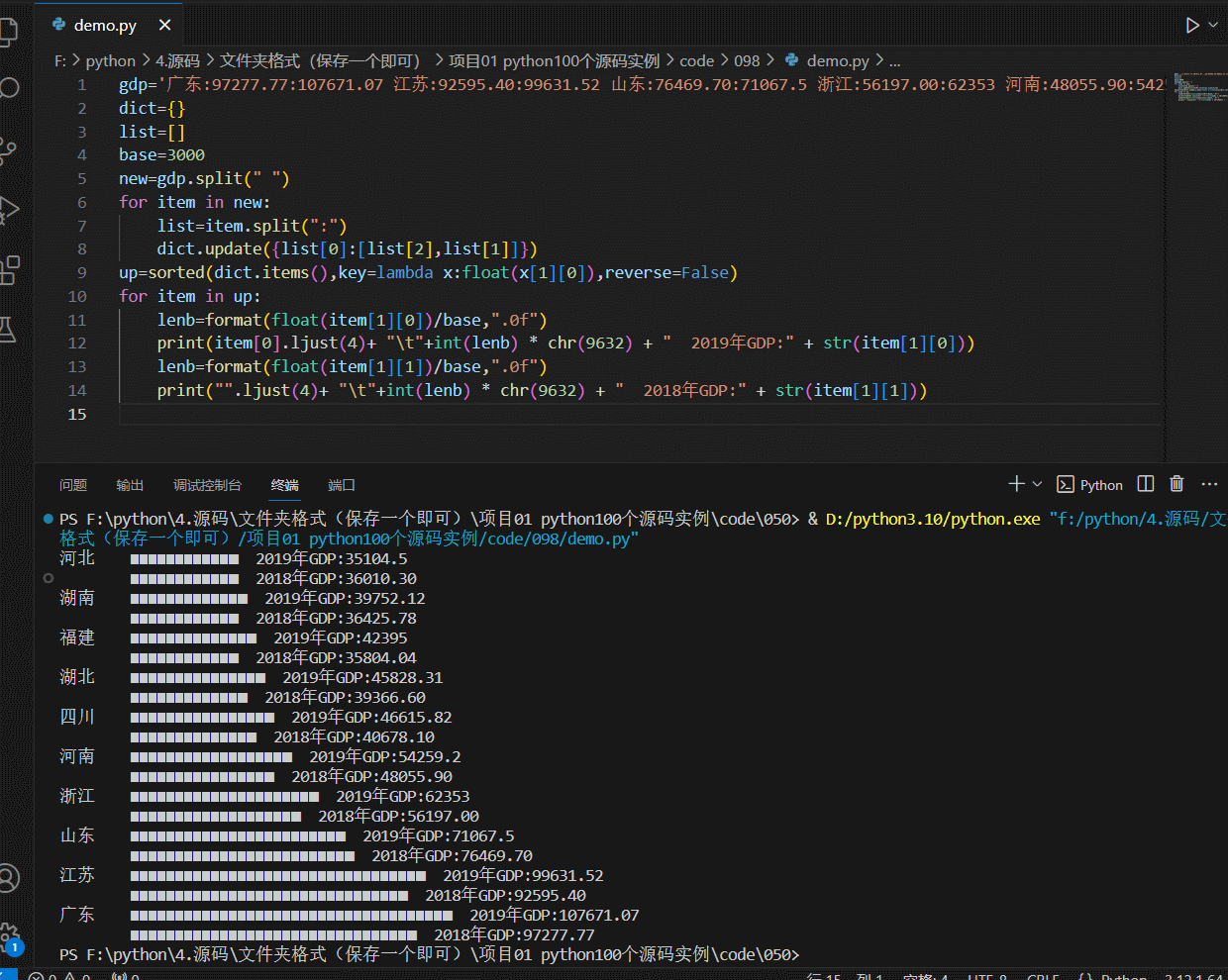
python-可视化篇-简单-条形图输出主要省份GDP排名情况
条形图输出主要省份GDP排名情况 代码 gdp广东:97277.77:107671.07 江苏:92595.40:99631.52 山东:76469.70:71067.5 浙江:56197.00:62353 河南:48055.90:54259.2 四川:40678.10:46615.82 湖北:39366.60:45828.31 湖南:36425.78:39752.12 河北:36010.30:35104.5 福建:35804.04:…...
Sora - 探索AI视频模型的无限可能-官方报告解读与思考
一、引言 最近SORA火爆刷屏,我也忍不住找来官方报告分析了一下,本文将深入探讨OpenAI最新发布的Sora模型。Sora模型不仅仅是一个视频生成器,它代表了一种全新的数据驱动物理引擎,能够在虚拟世界中模拟现实世界的复杂现象。本文将重…...

算法提升——LeetCode第385场周赛总结
题目 统计前后缀下标对 I 给你一个下标从0开始的字符串数组words。 定义一个布尔函数isPrefixAndSuffix,它接受两个字符串参数str1和str2: 当str1同时是str2的前缀(prefix)和后缀(suffix)时,…...
【README 小技巧】在项目README.md 中展示发布到maven 仓库版本
在项目README.md 中展示发不到nexus 的快照版本 <p align"center"><a target"_blank" href"https://search.maven.org/search?qwu-lazy-cloud-network%20wu-lazy-cloud-network"><img src"https://img-home.csdnimg.cn/ima…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...