LeetCode笔记:Biweekly Contest 99
- LeetCode笔记:Biweekly Contest 99
- 1. 题目一
- 1. 解题思路
- 2. 代码实现
- 2. 题目二
- 1. 解题思路
- 2. 代码实现
- 3. 题目三
- 1. 解题思路
- 2. 代码实现
- 4. 题目四
- 1. 解题思路
- 2. 代码实现
- 1. 题目一
- 比赛链接:https://leetcode.com/contest/biweekly-contest-99
1. 题目一
给出题目一的试题链接如下:
- 2578. Split With Minimum Sum
1. 解题思路
这一题题目简直有毒,题目强调了数字不会以0开头,但是没想到分开的数字却可以以0为开头,因此这道题事实上是被大幅简化了的,我们只要把每一位数排序然后交错分成两个数字相加即可。
2. 代码实现
给出python代码实现如下:
class Solution:def splitNum(self, num: int) -> int:s = str(num)s = sorted([int(ch) for ch in s])n1, n2 = 0, 0for i, ch in enumerate(s):if i % 2 == 0:n1 = n1 * 10 + chelse:n2 = n2 * 10 + chreturn n1 + n2
提交代码评测得到:耗时32ms,占用内存13.8MB。
2. 题目二
给出题目二的试题链接如下:
- 2579. Count Total Number of Colored Cells
1. 解题思路
这一题其实也简单,就是一个等差数列求和,一道数学题罢了,答案为:
ans=∑i=1n(2i−1)+∑i=1n−1(2i−1)=n2+(n−1)2\begin{aligned} ans &= \sum\limits_{i=1}^{n}(2i-1) + \sum\limits_{i=1}^{n-1}(2i-1) \\ &= n^2 + (n-1)^2 \end{aligned} ans=i=1∑n(2i−1)+i=1∑n−1(2i−1)=n2+(n−1)2
2. 代码实现
给出python代码实现如下:
class Solution:def coloredCells(self, n: int) -> int:return n * n + (n-1) * (n-1)
提交代码评测得到:耗时31ms,占用内存13.7MB。
3. 题目三
给出题目三的试题链接如下:
- 2580. Count Ways to Group Overlapping Ranges
1. 解题思路
这一题我们只需要将range进行一下排列,就能够快速地得到所有的有overlapping的区间,然后我们将这些区间分块,就能够得到所有不含有overlapping的区间块总数nnn,而我们的答案就是2n2^n2n。
2. 代码实现
给出python代码实现如下:
class Solution:def countWays(self, ranges: List[List[int]]) -> int:MOD = 10**9 + 7groups = 0ranges = sorted(ranges)rb = -1for a, b in ranges:if a > rb:groups += 1rb = belse:rb = max(rb, b)res = 1for _ in range(groups):res = res * 2 % MODreturn res
提交代码评测得到:耗时897ms,占用内存53.1MB。
4. 题目四
给出题目四的试题链接如下:
- 2581. Count Number of Possible Root Nodes
1. 解题思路
这一题感觉是这周的8道题里面最难的一题了,一开始我也没啥思路,中午的时候临机一动想到了答案,还是蛮开心的。
这一题本质上就是遍历一下每一个点作为根节点时,Bob提出的guess当中正确的猜测的个数,统计其中能够大于k的情况。
单独对于某一个点作为根节点的情况下,考察正确猜测的个数这件事其实是很简单的,只需要用一个遍历即可实现,但是要遍历所有的点作为根节点的情况,这个对于计算效率的要求就比较高了,肯定不都能用for循环对一个节点都单独计算。
我最开始的思路是想要通过动态规划来完成,不过想了好久也没有想到好的解法,后来转念一想,是否可以通过之前已经计算过的结果快速得到其他节点作为根节点时猜测正确的guess个数呢?
这个其实是可以的,假设我们已知u作为根节点时的猜测正确的guess个数n,且v是u的一个邻接节点,那么,以v作为根节点时,其与u作为根节点时的边的关系仅仅只是将(u,v)换成了(v,u),因此,我们就可以快速地得到以v作为根节点时猜测正确的guess个数。
我们同样使用一个遍历即可得到全部的答案了。
2. 代码实现
给出python代码实现如下:
class Solution:def rootCount(self, edges: List[List[int]], guesses: List[List[int]], k: int) -> int:n = len(edges) + 1graph = defaultdict(list)for u, v in edges:graph[u].append(v)graph[v].append(u)guesses = {(u,v) for u, v in guesses}cnt = 0q = [0]seen = set()while q != []:u = q.pop(0)seen.add(u)for v in graph[u]:if v in seen:continueif (u, v) in guesses:cnt += 1q.append(v)seen = set()res = 0def dfs(u, cnt):nonlocal seen, resif u in seen:return if cnt >= k:res += 1seen.add(u)for v in graph[u]:if (u, v) in guesses:if (v, u) in guesses:dfs(v, cnt)else:dfs(v, cnt-1)else:if (v, u) in guesses:dfs(v, cnt+1)else:dfs(v, cnt)returndfs(0, cnt)return res
提交代码评测得到:耗时2205ms,占用内存194.1MB。
相关文章:

LeetCode笔记:Biweekly Contest 99
LeetCode笔记:Biweekly Contest 99 1. 题目一 1. 解题思路2. 代码实现 2. 题目二 1. 解题思路2. 代码实现 3. 题目三 1. 解题思路2. 代码实现 4. 题目四 1. 解题思路2. 代码实现 比赛链接:https://leetcode.com/contest/biweekly-contest-99 1. 题目一…...

初探富文本之CRDT协同实例
初探富文本之CRDT协同实例 在前边初探富文本之CRDT协同算法一文中我们探讨了为什么需要协同、分布式的最终一致性理论、偏序集与半格的概念、为什么需要有偏序关系、如何通过数据结构避免冲突、分布式系统如何进行同步调度等等,这些属于完成协同所需要了解的基础知…...
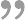
团队死气沉沉?10种玩法激活你的项目团队拥有超强凝聚力
作为项目经理和PMO,以及管理者最头疼的是团队的氛围和凝聚力,经常会发现团队死气沉沉,默不作声,你想尽办法也不能激活团队,也很难凝聚团队。这样的项目团队你很难带领大家去打胜仗,攻克堡垒。但是如何才能避…...

Spring三级缓存核心思想
spring在启动时候,会创建bean,并给bean填充属性,这事会使用到三级缓存 private final Map<String, Object> singletonObjects new ConcurrentHashMap<>(256); //一级缓存private final Map<String, Object> earlySingleto…...

深度学习算法训练和部署流程介绍--让初学者一篇文章彻底理解算法训练和部署流程
目录 1 什么是深度学习算法 2 算法训练 2.1 训练的原理 2.2 名词解释 3 算法C部署 3.1 嵌入式终端板子部署 3.3.1 tpu npu推理 3.3.2 cpu推理 3.2 服务器部署 3.2.1 智能推理 3.2.2 CPU推理 1 什么是深度学习算法 这里不去写复杂的概念,就用通俗的话说…...
计算机网络整理
TCP与UDP 介绍 HTTP:(HyperText Transport Protocol)是超文本传输协议的缩写,它用于传送WWW方式的数据,关于HTTP协议的详细内容请参考RFC2616。HTTP协议采用了请求/响应模型。 TCP:(Transmission Contro…...
闲人闲谈PS之三十八——混合制生产下WBS-BOM价格发布增强
惯例闲话:最近中《三体》的毒很深,可能是电视剧版确实给闲人这种原著粉带来太多的感动,又一次引发了怀旧的热潮,《我的三体-罗辑传》是每天睡前必刷的视频,结尾BGM太燃了。闲人对其中一句台词感触很深——人类不感谢罗…...

Java 根类 Object
java.lang.Object 是 Java 类层次结构中的根类,所有类都直接或间接实现了此类的方法。 Object API 源码 package java.lang;public class Object {private static native void registerNatives();static {registerNatives();}public final native Class<?>…...

04_Apache Pulsar的可视化监控管理、Apache Pulsar的可视化监控部署
1.4.Apache Pulsar的可视化监控管理 1.4.1.Apache Pulsar的可视化监控部署 1.4.Apache Pulsar的可视化监控管理 1.4.1.Apache Pulsar的可视化监控部署 第一步:下载Pulsar-Manager https://archive.apache.org/dist/pulsar/pulsar-manager/pulsar-manager-0.2.0/…...

【算法】期末复盘,酒店住宿问题——勿向思想僵化前进
文章目录前言题目描述卡在哪里代码(C)前言 省流:一个人也可以住双人间,如果便宜的话。 害!尚正值青春年华,黄金岁月,小脑瓜子就已经不灵光咯。好在我在考试的最后一分钟还是成功通过了这题&am…...
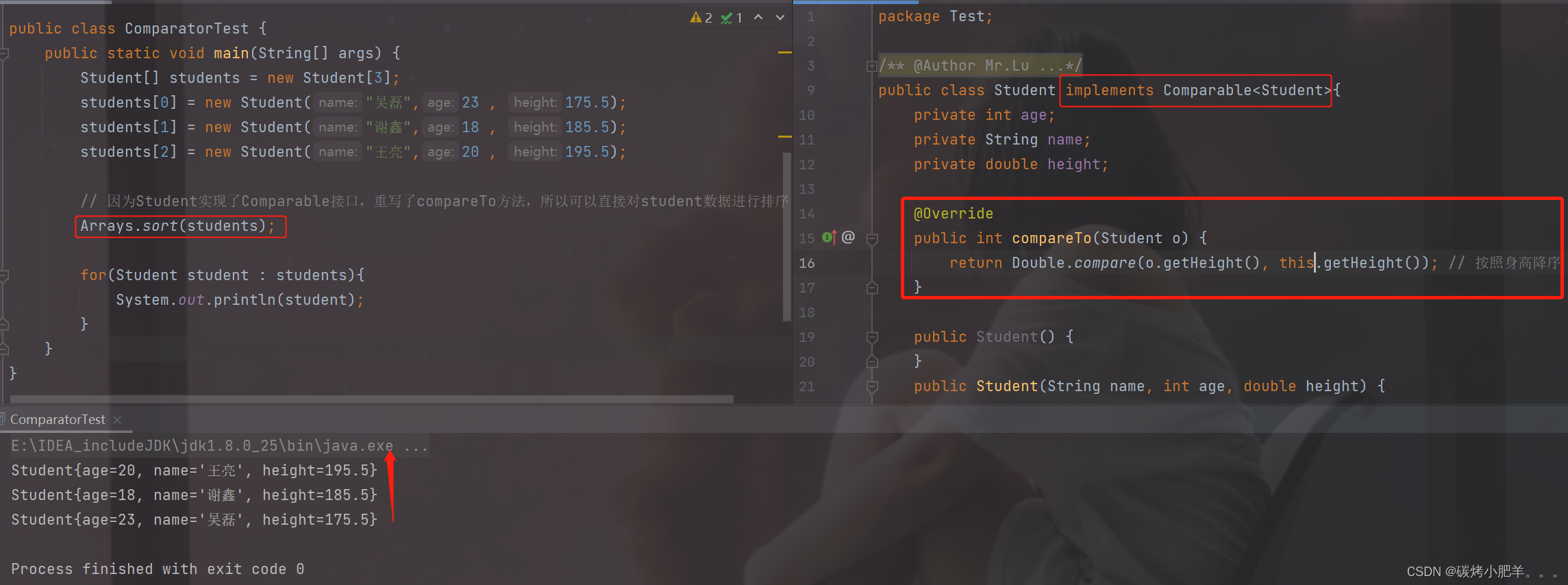
Java中的Comparator 与 Comparable详解
Comparator VS Comparable1. Comparator1.1 对一维数组进行排序1.2 对二维数组进行排序1.3 对对象数组进行排序2. Comparable3. 二者区别1. Comparator 通过源码发现Comparator是一个接口。 根据compare方法中的注释可以发现方法返回三种类型的值,正数、零、负数&a…...
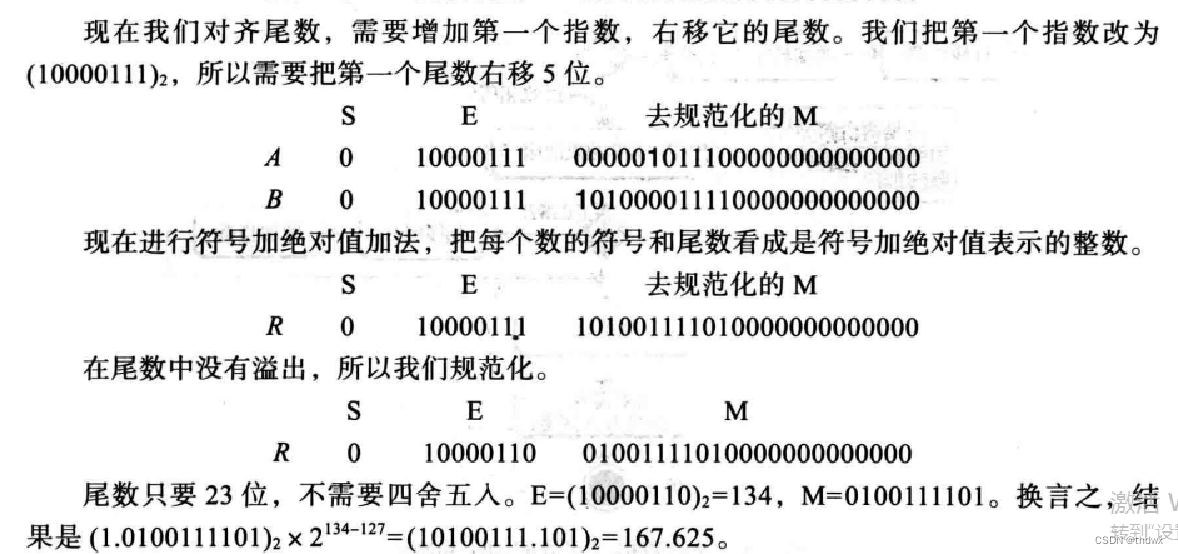
计算机科学导论笔记(二)
三、数据存储 3.1 数据类型 计算机行业中使用术语“多媒体”来定义包含数字、文本、音频、图像和视频的信息。 位:bit,binary digit的缩写,是存储在计算机中的最小单位,它是0或1. 位模式:为了表示数据的不同类型&a…...

GEC6818开发板JPG图像显示,科大讯飞离线语音识别包Linux_aitalk_exp1227_1398d7c6运行demo程序,开发板实现录音
GEC6818开发板JPG图像显示 | 开发板实现录音一.GEC6818开发板JPG图像显示1.jpg图片特性2.如何解压缩jpg图片1.对jpegsrc.v8c.tar.gz进行arm移植2.进入~/jpeg-8c对jpeg库进行配置3.编译4.安装,将动态库存放到 /home/gec/armJPegLib5.清空编译记录6.自己查看下 /home/…...

如何判断树莓派通过GPIO与5G模块成功连接?
如果想要判断自己是否成功连接了树莓派与5G模块,可以通过以下方式进行判断: 查看设备连接状态:可以通过在树莓派终端中执行lsusb命令来查看USB设备的连接状态,如果5G模块被识别到,则会显示相关的设备信息。如果提示lsu…...
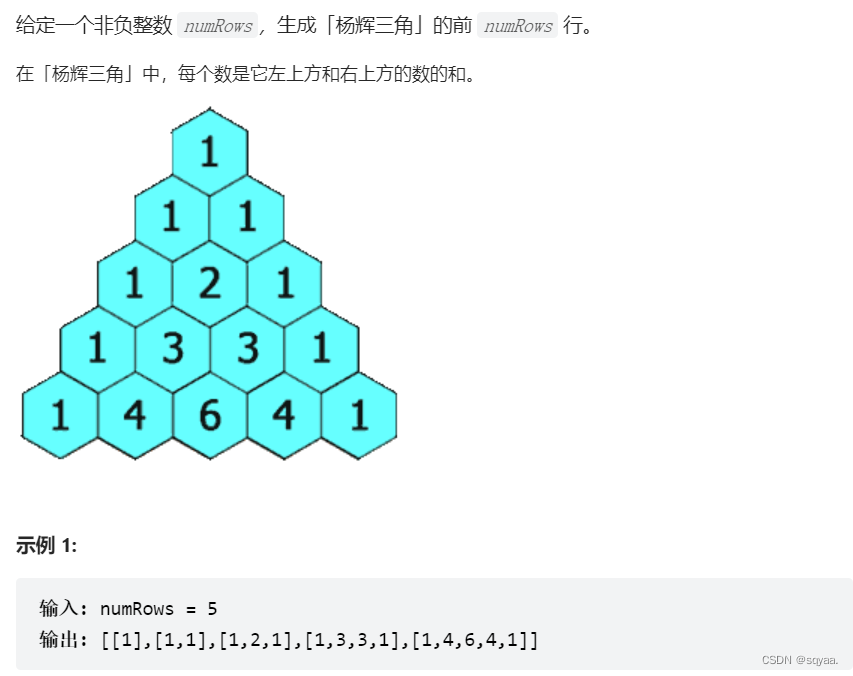
Java——包装类和List及ArrayList
目录 包装类(Wrapped Class) 包装类的使用---装箱和拆箱 自动装箱和自动拆箱 Integer的易错题 javap反编译工具 List接口的使用 方法 ArrayList 使用 打印 区别 扩容机制 ArrayList练习 字符集合 杨辉三角 编辑 包装类(Wrapped Class) Object 引用可…...
matlab - 程序流程控制、函数文件、特殊函数、调试与优化
学习视频MATLAB代码的两种执行方式:命令行、程序执行。1.程序流程控制1.1.m文件matlab中m文件分为两种:脚本文件&函数文件。脚本文件:实际上是一个命令的集合,可认为是命令行的改良版,方便我们去编写命令函数文件&…...

Toponogov 比较定理及其应用
1. Toponogov 比较定理的背景来源 Victor Andreevich Toponogov(1930-2004) 是苏联数学家,Toponogov 比较定理是他的博士论文题目,在1958年答辩。他证明这个定理是为了用于证明截面曲率假设下的分裂定理和最大直径定理࿰…...

力扣sql简单篇练习(二十二)
力扣sql简单篇练习(二十二) 1 上月播放的儿童适宜电影 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 a 示例输入 b 示例输出 1.2 示例sql语句 # Write your MySQL query statement belowSELECT titleFROM ContentWHERE kids_contentY AND content_typeMoviesAND c…...

【开源硬件】STM32F030R8T6系统板
【开源硬件】STM32F030R8T6系统板✅STM32F030R8T6系统板兼容极海APM32F030R8T6 🔰支持stm32cubemx工程配置成STM32F030R8T6生成的MDK工程,经过Keil编译后可以直接使用ST-Link v2烧录器上传到极海APM32F030R8T6芯片当中,完全做到平替使用&…...
ES之DSL查询文档基础查询
分类 query查询分类 总体规律就是逻辑性的,从外层的你干嘛,到下一层的查询类型,再到下一层的查询字段(如果需要的话)和然后是查询内容 查询所有 语法 get /索引库名/_serarch {"query":{"查询条件…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
