【数据结构与算法】(19)高级数据结构与算法设计之 图 拓扑排序 最短路径 最小生成树 不相交集合(并查集合)代码示例
目录
- 6) 拓扑排序
- Kahn
- DFS
- 7) 最短路径
- Dijkstra
- Bellman-Ford
- Floyd-Warshall
- 8) 最小生成树
- Prim
- Kruskal
- 9) 不相交集合(并查集合)
- 基础
- 路径压缩
- Union By Size
- 图-相关题目

6) 拓扑排序
Kahn
public class TopologicalSort {public static void main(String[] args) {Vertex v1 = new Vertex("网页基础");Vertex v2 = new Vertex("Java基础");Vertex v3 = new Vertex("JavaWeb");Vertex v4 = new Vertex("Spring框架");Vertex v5 = new Vertex("微服务框架");Vertex v6 = new Vertex("数据库");Vertex v7 = new Vertex("实战项目");v1.edges = List.of(new Edge(v3)); // +1v2.edges = List.of(new Edge(v3)); // +1v3.edges = List.of(new Edge(v4));v6.edges = List.of(new Edge(v4));v4.edges = List.of(new Edge(v5));v5.edges = List.of(new Edge(v7));v7.edges = List.of();List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6, v7);// 1. 统计每个顶点的入度for (Vertex v : graph) {for (Edge edge : v.edges) {edge.linked.inDegree++;}}/*for (Vertex vertex : graph) {System.out.println(vertex.name + " " + vertex.inDegree);}*/// 2. 将入度为0的顶点加入队列LinkedList<Vertex> queue = new LinkedList<>();for (Vertex v : graph) {if (v.inDegree == 0) {queue.offer(v);}}// 3. 队列中不断移除顶点,每移除一个顶点,把它相邻顶点入度减1,若减到0则入队List<String> result = new ArrayList<>();while (!queue.isEmpty()) {Vertex poll = queue.poll();
// System.out.println(poll.name);result.add(poll.name);for (Edge edge : poll.edges) {edge.linked.inDegree--;if (edge.linked.inDegree == 0) {queue.offer(edge.linked);}}}if (result.size() != graph.size()) {System.out.println("出现环");} else {for (String key : result) {System.out.println(key);}}}
}
DFS
public class TopologicalSortDFS {public static void main(String[] args) {Vertex v1 = new Vertex("网页基础");Vertex v2 = new Vertex("Java基础");Vertex v3 = new Vertex("JavaWeb");Vertex v4 = new Vertex("Spring框架");Vertex v5 = new Vertex("微服务框架");Vertex v6 = new Vertex("数据库");Vertex v7 = new Vertex("实战项目");v1.edges = List.of(new Edge(v3));v2.edges = List.of(new Edge(v3));v3.edges = List.of(new Edge(v4));v6.edges = List.of(new Edge(v4));v4.edges = List.of(new Edge(v5));v5.edges = List.of(new Edge(v7));v7.edges = List.of();List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6, v7);LinkedList<String> result = new LinkedList<>();for (Vertex v : graph) {if(v.status==0) {dfs(v, result);}}System.out.println(result);}private static void dfs(Vertex v, LinkedList<String> result) {if (v.status == 2) {return;}if (v.status == 1) {throw new RuntimeException("发现环");}v.status = 1;for (Edge edge : v.edges) {dfs(edge.linked, result);}v.status = 2;result.push(v.name);}
}
7) 最短路径
Dijkstra

Edsger Wybe Dijkstra
艾兹格·维布·迪克斯特拉(Edsger Wybe Dijkstra,/ˈdaɪkstrə/ DYKE-strə;荷兰语:[ˈɛtsxər ˈʋibə ˈdɛikstra] 1930年5月11日-2002年8月6日)是一位荷兰计算机科学家、程序员、软件工程师、系统科学家和科学散文家。他因对开发结构化编程语言做出的基础贡献而获得了1972年的图灵奖,并担任德克萨斯大学奥斯汀分校的斯伦贝谢百年计算机科学主席,任职时间从1984年到2000年。在他于2002年去世前不久,他因其在程序计算的自稳定性方面的工作而获得了ACM PODC分布式计算有影响力论文奖。为了纪念他,该年度奖项在接下来的一年更名为迪克斯特拉奖。
迪克斯特拉在计算机科学领域的贡献
- 最短路径算法,也称为迪克斯特拉算法,现代计算机科学本科课程中广泛教授
- Shunting yard算法
- THE OS 操作系统
- 银行家算法
- 用于协调多个处理器和程序的信号量构造
- 在分布式计算领域提出概念:自稳定性
算法描述:
- 将所有顶点标记为未访问。创建一个未访问顶点的集合。
- 为每个顶点分配一个临时距离值
- 对于我们的初始顶点,将其设置为零
- 对于所有其他顶点,将其设置为无穷大。
- 每次选择最小临时距离的未访问顶点,作为新的当前顶点
- 对于当前顶点,遍历其所有未访问的邻居,并更新它们的临时距离为更小
- 例如,1->6 的距离是 14,而1->3->6 的距离是11。这时将距离更新为 11
- 否则,将保留上次距离值
- 当前顶点的邻居处理完成后,把它从未访问集合中删除
public class Dijkstra {public static void main(String[] args) {Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");Vertex v5 = new Vertex("v5");Vertex v6 = new Vertex("v6");v1.edges = List.of(new Edge(v3, 9), new Edge(v2, 7), new Edge(v6, 14));v2.edges = List.of(new Edge(v4, 15));v3.edges = List.of(new Edge(v4, 11), new Edge(v6, 2));v4.edges = List.of(new Edge(v5, 6));v5.edges = List.of();v6.edges = List.of(new Edge(v5, 9));List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6);dijkstra(graph, v1);}private static void dijkstra(List<Vertex> graph, Vertex source) {ArrayList<Vertex> list = new ArrayList<>(graph);source.dist = 0;while (!list.isEmpty()) {// 3. 选取当前顶点Vertex curr = chooseMinDistVertex(list);// 4. 更新当前顶点邻居距离updateNeighboursDist(curr, list);// 5. 移除当前顶点list.remove(curr);}for (Vertex v : graph) {System.out.println(v.name + " " + v.dist);}}private static void updateNeighboursDist(Vertex curr, ArrayList<Vertex> list) {for (Edge edge : curr.edges) {Vertex n = edge.linked;if (list.contains(n)) {int dist = curr.dist + edge.weight;if (dist < n.dist) {n.dist = dist;}}}}private static Vertex chooseMinDistVertex(ArrayList<Vertex> list) {Vertex min = list.get(0);for (int i = 1; i < list.size(); i++) {if (list.get(i).dist < min.dist) {min = list.get(i);}}return min;}}
改进 - 优先级队列
- 创建一个优先级队列,放入所有顶点(队列大小会达到边的数量)
- 为每个顶点分配一个临时距离值
- 对于我们的初始顶点,将其设置为零
- 对于所有其他顶点,将其设置为无穷大。
- 每次选择最小临时距离的未访问顶点,作为新的当前顶点
- 对于当前顶点,遍历其所有未访问的邻居,并更新它们的临时距离为更小,若距离更新需加入队列
- 例如,1->6 的距离是 14,而1->3->6 的距离是11。这时将距离更新为 11
- 否则,将保留上次距离值
- 当前顶点的邻居处理完成后,把它从队列中删除
public class DijkstraPriorityQueue {public static void main(String[] args) {Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");Vertex v5 = new Vertex("v5");Vertex v6 = new Vertex("v6");v1.edges = List.of(new Edge(v3, 9), new Edge(v2, 7), new Edge(v6, 14));v2.edges = List.of(new Edge(v4, 15));v3.edges = List.of(new Edge(v4, 11), new Edge(v6, 2));v4.edges = List.of(new Edge(v5, 6));v5.edges = List.of();v6.edges = List.of(new Edge(v5, 9));List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6);dijkstra(graph, v1);}private static void dijkstra(List<Vertex> graph, Vertex source) {PriorityQueue<Vertex> queue = new PriorityQueue<>(Comparator.comparingInt(v -> v.dist));source.dist = 0;for (Vertex v : graph) {queue.offer(v);}while (!queue.isEmpty()) {System.out.println(queue);// 3. 选取当前顶点Vertex curr = queue.peek();// 4. 更新当前顶点邻居距离if(!curr.visited) {updateNeighboursDist(curr, queue);curr.visited = true;}// 5. 移除当前顶点queue.poll();}for (Vertex v : graph) {System.out.println(v.name + " " + v.dist + " " + (v.prev != null ? v.prev.name : "null"));}}private static void updateNeighboursDist(Vertex curr, PriorityQueue<Vertex> queue) {for (Edge edge : curr.edges) {Vertex n = edge.linked;if (!n.visited) {int dist = curr.dist + edge.weight;if (dist < n.dist) {n.dist = dist;n.prev = curr;queue.offer(n);}}}}}
问题
按照 Dijkstra 算法,得出
- v1 -> v2 最短距离2
- v1 -> v3 最短距离1
- v1 -> v4 最短距离2
事实应当是
- v1 -> v2 最短距离2
- v1 -> v3 最短距离0
- v1 -> v4 最短距离1
Bellman-Ford
public class BellmanFord {public static void main(String[] args) {// 正常情况/*Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");Vertex v5 = new Vertex("v5");Vertex v6 = new Vertex("v6");v1.edges = List.of(new Edge(v3, 9), new Edge(v2, 7), new Edge(v6, 14));v2.edges = List.of(new Edge(v4, 15));v3.edges = List.of(new Edge(v4, 11), new Edge(v6, 2));v4.edges = List.of(new Edge(v5, 6));v5.edges = List.of();v6.edges = List.of(new Edge(v5, 9));List<Vertex> graph = List.of(v4, v5, v6, v1, v2, v3);*/// 负边情况/*Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");v1.edges = List.of(new Edge(v2, 2), new Edge(v3, 1));v2.edges = List.of(new Edge(v3, -2));v3.edges = List.of(new Edge(v4, 1));v4.edges = List.of();List<Vertex> graph = List.of(v1, v2, v3, v4);*/// 负环情况Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");v1.edges = List.of(new Edge(v2, 2));v2.edges = List.of(new Edge(v3, -4));v3.edges = List.of(new Edge(v4, 1), new Edge(v1, 1));v4.edges = List.of();List<Vertex> graph = List.of(v1, v2, v3, v4);bellmanFord(graph, v1);}private static void bellmanFord(List<Vertex> graph, Vertex source) {source.dist = 0;int size = graph.size();// 1. 进行 顶点个数 - 1 轮处理for (int i = 0; i < size - 1; i++) {// 2. 遍历所有的边for (Vertex s : graph) {for (Edge edge : s.edges) {// 3. 处理每一条边Vertex e = edge.linked;if (s.dist != Integer.MAX_VALUE && s.dist + edge.weight < e.dist) {e.dist = s.dist + edge.weight;e.prev = s;}}}}for (Vertex v : graph) {System.out.println(v + " " + (v.prev != null ? v.prev.name : "null"));}}
}
负环
如果在【顶点-1】轮处理完成后,还能继续找到更短距离,表示发现了负环
Floyd-Warshall
public class FloydWarshall {public static void main(String[] args) {Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");v1.edges = List.of(new Edge(v3, -2));v2.edges = List.of(new Edge(v1, 4), new Edge(v3, 3));v3.edges = List.of(new Edge(v4, 2));v4.edges = List.of(new Edge(v2, -1));List<Vertex> graph = List.of(v1, v2, v3, v4);/*直接连通v1 v2 v3 v4v1 0 ∞ -2 ∞v2 4 0 3 ∞v3 ∞ ∞ 0 2v4 ∞ -1 ∞ 0k=0 借助v1到达其它顶点v1 v2 v3 v4v1 0 ∞ -2 ∞v2 4 0 2 ∞v3 ∞ ∞ 0 2v4 ∞ -1 ∞ 0k=1 借助v2到达其它顶点v1 v2 v3 v4v1 0 ∞ -2 ∞v2 4 0 2 ∞v3 ∞ ∞ 0 2v4 3 -1 1 0k=2 借助v3到达其它顶点v1 v2 v3 v4v1 0 ∞ -2 0v2 4 0 2 4v3 ∞ ∞ 0 2v4 3 -1 1 0k=3 借助v4到达其它顶点v1 v2 v3 v4v1 0 -1 -2 0v2 4 0 2 4v3 5 1 0 2v4 3 -1 1 0*/floydWarshall(graph);}static void floydWarshall(List<Vertex> graph) {int size = graph.size();int[][] dist = new int[size][size];Vertex[][] prev = new Vertex[size][size];// 1)初始化for (int i = 0; i < size; i++) {Vertex v = graph.get(i); // v1 (v3)Map<Vertex, Integer> map = v.edges.stream().collect(Collectors.toMap(e -> e.linked, e -> e.weight));for (int j = 0; j < size; j++) {Vertex u = graph.get(j); // v3if (v == u) {dist[i][j] = 0;} else {dist[i][j] = map.getOrDefault(u, Integer.MAX_VALUE);prev[i][j] = map.get(u) != null ? v : null;}}}print(prev);// 2)看能否借路到达其它顶点/*v2->v1 v1->v?dist[1][0] + dist[0][0]dist[1][0] + dist[0][1]dist[1][0] + dist[0][2]dist[1][0] + dist[0][3]*/for (int k = 0; k < size; k++) {for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {
// dist[i][k] + dist[k][j] // i行的顶点,借助k顶点,到达j列顶点
// dist[i][j] // i行顶点,直接到达j列顶点if (dist[i][k] != Integer.MAX_VALUE &&dist[k][j] != Integer.MAX_VALUE &&dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];prev[i][j] = prev[k][j];}}}
// print(dist);}print(prev);}static void path(Vertex[][] prev, List<Vertex> graph, int i, int j) {LinkedList<String> stack = new LinkedList<>();System.out.print("[" + graph.get(i).name + "," + graph.get(j).name + "] ");stack.push(graph.get(j).name);while (i != j) {Vertex p = prev[i][j];stack.push(p.name);j = graph.indexOf(p);}System.out.println(stack);}static void print(int[][] dist) {System.out.println("-------------");for (int[] row : dist) {System.out.println(Arrays.stream(row).boxed().map(x -> x == Integer.MAX_VALUE ? "∞" : String.valueOf(x)).map(s -> String.format("%2s", s)).collect(Collectors.joining(",", "[", "]")));}}static void print(Vertex[][] prev) {System.out.println("-------------------------");for (Vertex[] row : prev) {System.out.println(Arrays.stream(row).map(v -> v == null ? "null" : v.name).map(s -> String.format("%5s", s)).collect(Collectors.joining(",", "[", "]")));}}}
负环
如果在 3 层循环结束后,在 dist 数组的对角线处(i==j 处)发现了负数,表示出现了负环
8) 最小生成树
Prim
public class Prim {public static void main(String[] args) {Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");Vertex v5 = new Vertex("v5");Vertex v6 = new Vertex("v6");Vertex v7 = new Vertex("v7");v1.edges = List.of(new Edge(v2, 2), new Edge(v3, 4), new Edge(v4, 1));v2.edges = List.of(new Edge(v1, 2), new Edge(v4, 3), new Edge(v5, 10));v3.edges = List.of(new Edge(v1, 4), new Edge(v4, 2), new Edge(v6, 5));v4.edges = List.of(new Edge(v1, 1), new Edge(v2, 3), new Edge(v3, 2),new Edge(v5, 7), new Edge(v6, 8), new Edge(v7, 4));v5.edges = List.of(new Edge(v2, 10), new Edge(v4, 7), new Edge(v7, 6));v6.edges = List.of(new Edge(v3, 5), new Edge(v4, 8), new Edge(v7, 1));v7.edges = List.of(new Edge(v4, 4), new Edge(v5, 6), new Edge(v6, 1));List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6, v7);prim(graph, v1);}static void prim(List<Vertex> graph, Vertex source) {ArrayList<Vertex> list = new ArrayList<>(graph);source.dist = 0;while (!list.isEmpty()) {Vertex min = chooseMinDistVertex(list);updateNeighboursDist(min);list.remove(min);min.visited = true;System.out.println("---------------");for (Vertex v : graph) {System.out.println(v);}}}private static void updateNeighboursDist(Vertex curr) {for (Edge edge : curr.edges) {Vertex n = edge.linked;if (!n.visited) {int dist = edge.weight;if (dist < n.dist) {n.dist = dist;n.prev = curr;}}}}private static Vertex chooseMinDistVertex(ArrayList<Vertex> list) {Vertex min = list.get(0);for (int i = 1; i < list.size(); i++) {if (list.get(i).dist < min.dist) {min = list.get(i);}}return min;}
}
Kruskal
public class Kruskal {static class Edge implements Comparable<Edge> {List<Vertex> vertices;int start;int end;int weight;public Edge(List<Vertex> vertices, int start, int end, int weight) {this.vertices = vertices;this.start = start;this.end = end;this.weight = weight;}public Edge(int start, int end, int weight) {this.start = start;this.end = end;this.weight = weight;}@Overridepublic int compareTo(Edge o) {return Integer.compare(this.weight, o.weight);}@Overridepublic String toString() {return vertices.get(start).name + "<->" + vertices.get(end).name + "(" + weight + ")";}}public static void main(String[] args) {Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");Vertex v5 = new Vertex("v5");Vertex v6 = new Vertex("v6");Vertex v7 = new Vertex("v7");List<Vertex> vertices = List.of(v1, v2, v3, v4, v5, v6, v7);PriorityQueue<Edge> queue = new PriorityQueue<>(List.of(new Edge(vertices,0, 1, 2),new Edge(vertices,0, 2, 4),new Edge(vertices,0, 3, 1),new Edge(vertices,1, 3, 3),new Edge(vertices,1, 4, 10),new Edge(vertices,2, 3, 2),new Edge(vertices,2, 5, 5),new Edge(vertices,3, 4, 7),new Edge(vertices,3, 5, 8),new Edge(vertices,3, 6, 4),new Edge(vertices,4, 6, 6),new Edge(vertices,5, 6, 1)));kruskal(vertices.size(), queue);}static void kruskal(int size, PriorityQueue<Edge> queue) {List<Edge> result = new ArrayList<>();DisjointSet set = new DisjointSet(size);while (result.size() < size - 1) {Edge poll = queue.poll();int s = set.find(poll.start);int e = set.find(poll.end);if (s != e) {result.add(poll);set.union(s, e);}}for (Edge edge : result) {System.out.println(edge);}}
}
9) 不相交集合(并查集合)
基础
public class DisjointSet {int[] s;// 索引对应顶点// 元素是用来表示与之有关系的顶点/*索引 0 1 2 3 4 5 6元素 [0, 1, 2, 3, 4, 5, 6] 表示一开始顶点直接没有联系(只与自己有联系)*/public DisjointSet(int size) {s = new int[size];for (int i = 0; i < size; i++) {s[i] = i;}}// find 是找到老大public int find(int x) {if (x == s[x]) {return x;}return find(s[x]);}// union 是让两个集合“相交”,即选出新老大,x、y 是原老大索引public void union(int x, int y) {s[y] = x;}@Overridepublic String toString() {return Arrays.toString(s);}}
路径压缩
public int find(int x) { // x = 2if (x == s[x]) {return x;}return s[x] = find(s[x]); // 0 s[2]=0
}
Union By Size
public class DisjointSetUnionBySize {int[] s;int[] size;public DisjointSetUnionBySize(int size) {s = new int[size];this.size = new int[size];for (int i = 0; i < size; i++) {s[i] = i;this.size[i] = 1;}}// find 是找到老大 - 优化:路径压缩public int find(int x) { // x = 2if (x == s[x]) {return x;}return s[x] = find(s[x]); // 0 s[2]=0}// union 是让两个集合“相交”,即选出新老大,x、y 是原老大索引public void union(int x, int y) {
// s[y] = x;if (size[x] < size[y]) {int t = x;x = y;y = t;}s[y] = x;size[x] = size[x] + size[y];}@Overridepublic String toString() {return "内容:"+Arrays.toString(s) + "\n大小:" + Arrays.toString(size);}public static void main(String[] args) {DisjointSetUnionBySize set = new DisjointSetUnionBySize(5);set.union(1, 2);set.union(3, 4);set.union(1, 3);System.out.println(set);}}
图-相关题目
| 题目编号 | 题目标题 | 算法思想 |
|---|---|---|
| 547 | 省份数量 | DFS、BFS、并查集 |
| 797 | 所有可能路径 | DFS、BFS |
| 1584 | 连接所有点的最小费用 | 最小生成树 |
| 743 | 网络延迟时间 | 单源最短路径 |
| 787 | K 站中转内最便宜的航班 | 单源最短路径 |
| 207 | 课程表 | 拓扑排序 |
| 210 | 课程表 II | 拓扑排序 |
相关文章:

【数据结构与算法】(19)高级数据结构与算法设计之 图 拓扑排序 最短路径 最小生成树 不相交集合(并查集合)代码示例
目录 6) 拓扑排序KahnDFS 7) 最短路径DijkstraBellman-FordFloyd-Warshall 8) 最小生成树PrimKruskal 9) 不相交集合(并查集合)基础路径压缩Union By Size 图-相关题目 6) 拓扑排序 #mermaid-svg-MQhLsXiMwnlUL3q4 {font-family:"trebuchet ms"…...

OSCP靶场--Nickel
OSCP靶场–Nickel 考点(1.POST方法请求信息 2.ftp,ssh密码复用 3.pdf文件密码爆破) 1.nmap扫描 ┌──(root㉿kali)-[~/Desktop] └─# nmap 192.168.237.99 -sV -sC -p- --min-rate 5000 Starting Nmap 7.92 ( https://nmap.org ) at 2024-02-22 04:06 EST Nm…...

新建工程——库函数版
新建工程——库函数版 s t e p I : 新建工程文件夹 \bf{stepI:新建工程文件夹} stepI:新建工程文件夹 s t e p I I : K e i l 5 新建工程 \bf{stepII:Keil5新建工程} stepII:Keil5新建工程 s t e p I I I : 最终得到工程文件 \bf{stepIII:最终得到工程文件} stepIII:最终得到工…...
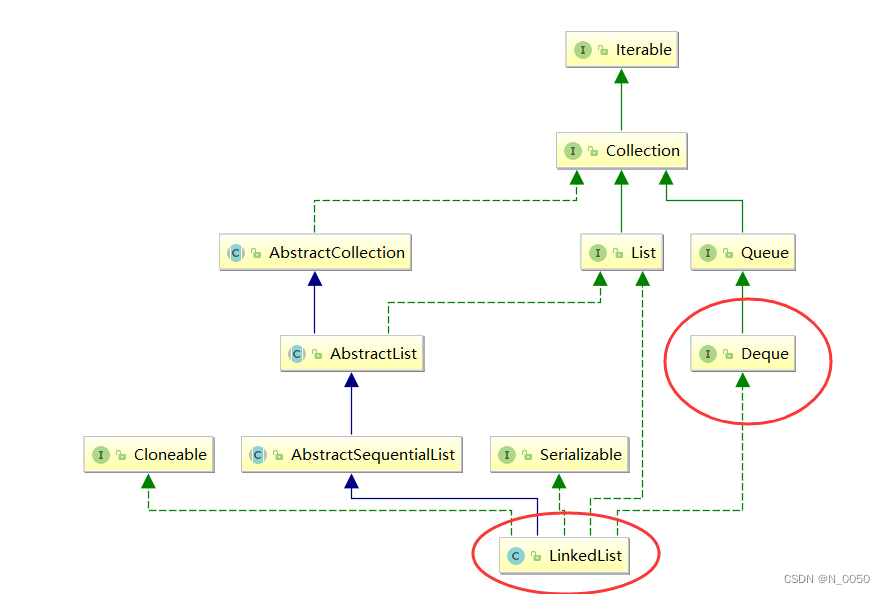
java 数据结构栈和队列
目录 栈(Stack) 栈的使用 栈的模拟实现 栈的应用场景 队列(Queue) 队列的使用 队列模拟实现 循环队列 双端队列 用队列实现栈 用栈实现队列 栈(Stack) 什么是栈? 栈 :一种特殊的线性表,其 只允许在固定的一端进行插入和删除元素操…...

#LLM入门|Prompt#1.8_聊天机器人_Chatbot
聊天机器人设计 以会话形式进行交互,接受一系列消息作为输入,并返回模型生成的消息作为输出。原本设计用于简便多轮对话,但同样适用于单轮任务。 设计思路 个性化特性:通过定制模型的训练数据和参数,使机器人拥有特…...
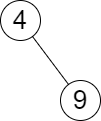
LeetCode 2476.二叉搜索树最近节点查询:中序遍历 + 二分查找
【LetMeFly】2476.二叉搜索树最近节点查询:中序遍历 二分查找 力扣题目链接:https://leetcode.cn/problems/closest-nodes-queries-in-a-binary-search-tree/ 给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 qu…...

选座位 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C 题目描述 疫情期间,需要大家保证一定的社交距离,公司组织开交流会议,座位有一排共N个座位,编号分别为[0…N-1],要…...
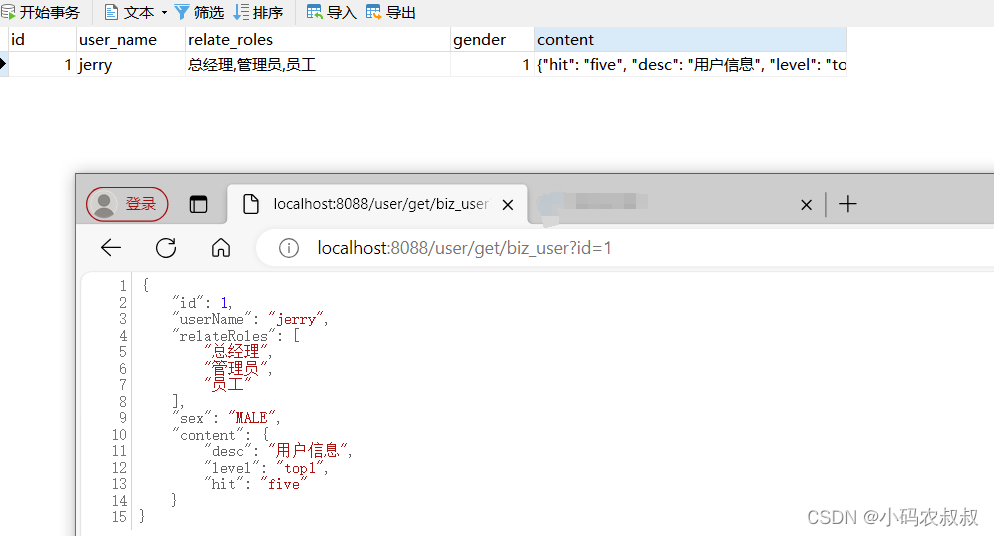
【微服务】mybatis typehandler使用详解
目录 一、前言 二、TypeHandler简介 2.1 什么是TypeHandler 2.1.1 TypeHandler特点 2.2 TypeHandler原理 2.3 mybatis自带的TypeHandler 三、环境准备 3.1 准备一张数据表 3.2 搭建一个springboot工程 3.2.1 基础依赖如下 3.2.2 核心配置文件 3.2.3 测试接口 四、T…...

计网 - 深入理解HTTPS:加密技术的背后
文章目录 Pre发展历史Http VS HttpsHTTPS 解决了 HTTP 的哪些问题HTTPS是如何解决上述三个风险的混合加密摘要算法 数字签名数字证书 Pre PKI - 数字签名与数字证书 PKI - 借助Nginx 实现Https 服务端单向认证、服务端客户端双向认证 发展历史 HTTP(超文本传输协…...

Jmeter之单接口的性能测试
前言: 服务端的整体性能测试是一个非常复杂的概念,包含生成虚拟用户,模拟并发,分析性能结果等各种技术,期间可能还要解决设计场景、缓存影响、第三方接口mock、IP限制等问题。如何用有限的测试机器,在测试环…...

成像光谱遥感技术中的AI革命:ChatGPT应用指南
“成像光谱遥感技术中的人工智能革命:ChatGPT应用指南”,这是一门旨在改变您使用人工智能处理遥感数据的方式。将最新的人工智能技术与实际的遥感应用相结合,提供不仅是理论上的,而且是适用和可靠的工具和方法。无论你是经验丰富的…...

掌握BeautifulSoup4:爬虫解析器的基础与实战【第91篇—BeautifulSoup4】
掌握BeautifulSoup4:爬虫解析器的基础与实战 网络上的信息浩如烟海,而爬虫技术正是帮助我们从中获取有用信息的重要工具。在爬虫过程中,解析HTML页面是一个关键步骤,而BeautifulSoup4正是一款功能强大的解析器,能够轻…...

从源码解析Kruise(K8S)原地升级原理
从源码解析Kruise原地升级原理 本文从源码的角度分析 Kruise 原地升级相关功能的实现。 本篇Kruise版本为v1.5.2。 Kruise项目地址: https://github.com/openkruise/kruise 更多云原生、K8S相关文章请点击【专栏】查看! 原地升级的概念 当我们使用deployment等Wor…...

2024年【广东省安全员C证第四批(专职安全生产管理人员)】复审考试及广东省安全员C证第四批(专职安全生产管理人员)模拟考试题
题库来源:安全生产模拟考试一点通公众号小程序 广东省安全员C证第四批(专职安全生产管理人员)复审考试是安全生产模拟考试一点通总题库中生成的一套广东省安全员C证第四批(专职安全生产管理人员)模拟考试题࿰…...
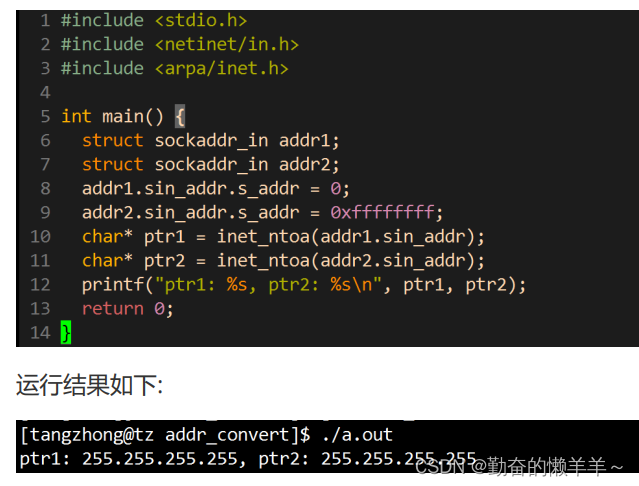
udp服务器【Linux网络编程】
目录 一、UDP服务器 1、创建套接字 2、绑定套接字 3、运行 1)读取数据 2)发送数据 二、UDP客户端 创建套接字: 客户端不用手动bind 收发数据 处理消息和网络通信解耦 三、应用场景 1、服务端执行命令 2、Windows上的客户端 3…...
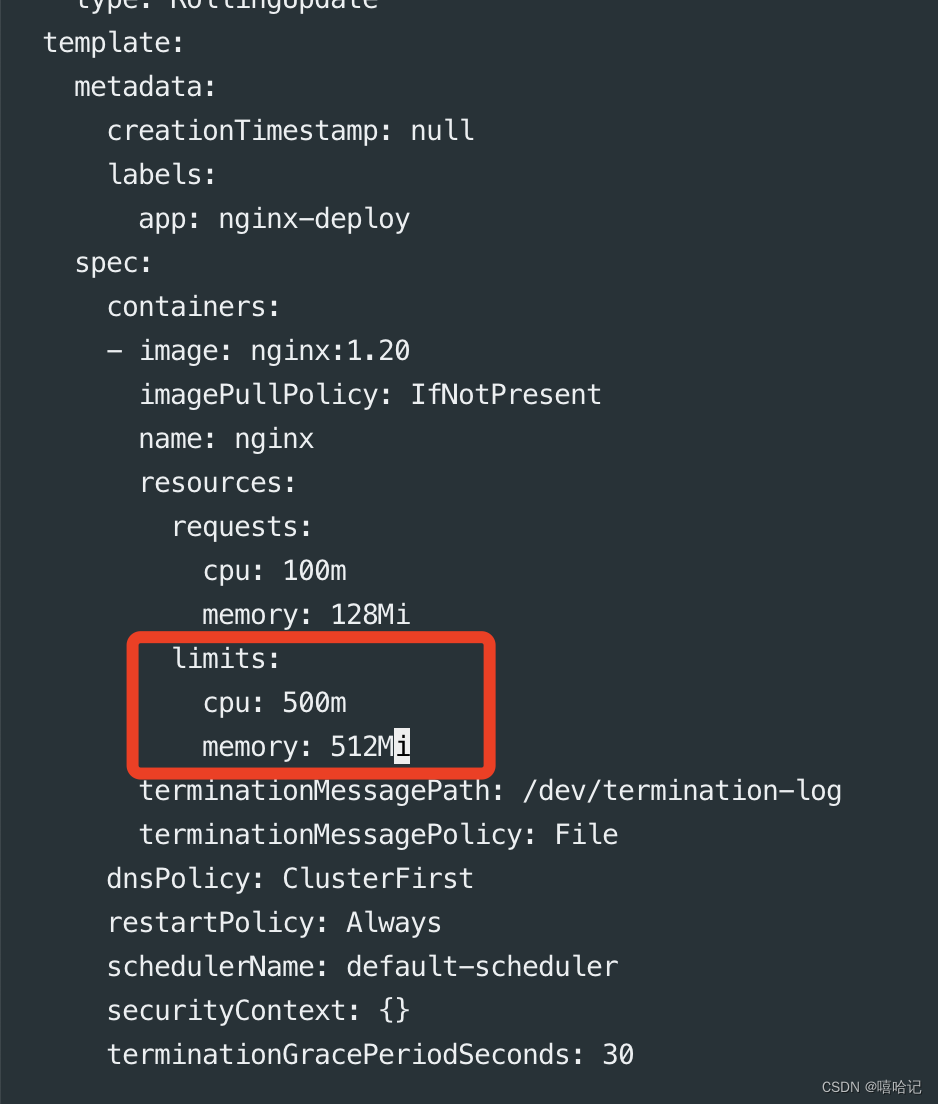
【k8s资源调度-Deployment】
1、标签和选择器 1.1 标签Label 配置文件:在各类资源的sepc.metadata.label 中进行配置通过kubectl 命令行创建修改标签,语法如下 创建临时label:kubectl label po <资源名称> apphello -n <命令空间(可不加࿰…...
【Oracle】玩转Oracle数据库(五):PL/SQL编程
前言 嗨,各位数据库达人!准备好迎接数据库编程的新挑战了吗?今天我们要探索的是Oracle数据库中的神秘魔法——PL/SQL编程!🔮💻 在这篇博文【Oracle】玩转Oracle数据库(五)࿱…...
JavaScript流程控制
文章目录 1. 顺序结构2. 分支结构2.1 if 语句2.2 if else 双分支语句2.3 if else if 多分支语句三元表达式 2.4 switch 语句switch 语句和 if else if语句区别 3. 循环结构3.1 for 循环断点调试 3.2 双重 for 循环3.3 while 循环3.4 do while 循环3.5 contiue break 关键字 4. …...

五个使用Delphi语言进行开发的案例
案例一:学生信息管理系统 某学校需要开发一个学生信息管理系统,用于记录学生的基本信息、成绩和考勤情况等。开发者使用Delphi语言进行开发,设计了一个包含多个窗体的应用程序。主窗体用于展示学生的列表和基本信息,其他窗体则用…...

蓝桥杯第1374题——锻造兵器
题目描述 小明一共有n块锻造石,第块锻造石的属性值为ai. 现在小明决定从这n块锻造石中任取两块来锻造兵器 通过周密计算,小明得出,只有当两块锻造石的属性值的差值等于C,兵器才能锻造成功 请你帮小明算算,他有多少种选…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
