后轮位置反馈控制与算法仿真实现
文章目录
- 1. 后轮反馈控制
- 2. 算法原理
- 3. 算法和仿真实现
1. 后轮反馈控制
后轮反馈控制(Rear wheel feedback)算法是利用后轮中心的跟踪偏差来进行转向控制量计算的方法,属于Frenet坐标系的一个应用。通过选择合适的李雅普诺夫函数设计控制率,利用后轮中心的跟踪偏差来进行转向控制量计算的方法。
2. 算法原理

后轮反馈控制算法原理如上图所示,其中
-
P P P:当前距离车辆最近的路经点;
-
e y e_y ey: P P P点与车辆后轮中心点的横向偏差 A P AP AP,实际上对应的就是frenet坐标下的 l l l;
-
φ \varphi φ:车辆朝向与 X X X轴正方向的夹角,即航向角;
-
φ r \varphi_{r} φr: P P P点切线与 X X X轴正方向的夹角;
-
φ e \varphi_e φe:车辆航向角误差,即 φ − φ r \varphi-\varphi_{r} φ−φr;
-
n τ ⃗ \vec{n_\tau} nτ: P P P点法线的单位向量;
-
τ r ⃗ \vec{\tau_r} τr: P P P点切线的单位向量;
-
L L L:轴距
-
δ f \delta_f δf:前轮转角
-
v v v:车辆的速度
由前面的文章frenet坐标与cartesian坐标相互转换与代码实现和上图的几何关系可得车辆在参考轨迹上的投影点 P P P处的线速度 s ˙ \dot{s} s˙和横向误差 e y e_y ey(即对应frenet坐标系下的 l ˙ \dot{l} l˙)的表达式为
s ˙ = v ⃗ τ r ⃗ 1 − k r l = ∣ v ⃗ ∣ ∣ τ r ⃗ ∣ c o s φ e 1 − k r e y = ∣ v ⃗ ∣ c o s φ e 1 − k r e y (1) \dot{s}=\frac{\vec{v} \vec{\tau_r}}{1-k_rl} = \frac{|\vec{v}| |\vec{\tau_r}|cos{\varphi_e}}{1-k_re_y}=\frac{|\vec{v}|cos{\varphi_e}}{1-k_re_y} \tag{1} s˙=1−krlvτr=1−krey∣v∣∣τr∣cosφe=1−krey∣v∣cosφe(1)
e y ˙ = l ˙ = v ⃗ n r ⃗ = ∣ v ⃗ ∣ ∣ n r ⃗ ∣ c o s ( π 2 − φ e ) = ∣ v ⃗ ∣ s i n φ e (2) \dot{e_y}=\dot{l}= \vec{v} \vec{n_r}= |\vec{v}| |\vec{n_r}| cos({\frac{\pi}{2}-\varphi_e}) = |\vec{v}| sin{\varphi_e} \tag{2} ey˙=l˙=vnr=∣v∣∣nr∣cos(2π−φe)=∣v∣sinφe(2)
由图中几何关系可得航向误差为
φ e = φ − φ r (3) \varphi_e = \varphi-\varphi_{r} \tag{3} φe=φ−φr(3)
则航向误差变化率为
φ e ˙ = φ ˙ − φ r ˙ = φ ˙ − s ˙ R r = φ ˙ − s ˙ k r (4) \dot{\varphi_e} = \dot{\varphi}-\dot{\varphi_{r}} = \dot{\varphi}-\frac{\dot{s}}{R_r }= \dot{\varphi}-\dot{s}k_r \tag{4} φe˙=φ˙−φr˙=φ˙−Rrs˙=φ˙−s˙kr(4)
注:一个刚体的角速度 = 线速度/线速度到速度瞬心的距离,上式中 R r R_r Rr为点 P P P处的瞬时圆心半径。
将(1)代入(4)可得
φ e ˙ = φ ˙ − s ˙ k r = φ ˙ − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y (4) \dot{\varphi_e} = \dot{\varphi}-\dot{s}k_r = \dot{\varphi}-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}\tag{4} φe˙=φ˙−s˙kr=φ˙−1−kreykr∣v∣cosφe(4)
综上可得后轮反馈控制算法对应模型的微分方程为
{ s ˙ = ∣ v ⃗ ∣ c o s φ e 1 − k r e y e y ˙ = ∣ v ⃗ ∣ s i n φ e φ e ˙ = φ ˙ − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y (5) \begin{cases} \dot{s}&=\quad \frac{|\vec{v}|cos{\varphi_e}}{1-k_re_y} \\ \dot{e_y}&=\quad |\vec{v}| sin{\varphi_e}\\ \dot{\varphi_e} &=\quad \dot{\varphi}-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y} \end{cases} \tag{5} ⎩ ⎨ ⎧s˙ey˙φe˙=1−krey∣v∣cosφe=∣v∣sinφe=φ˙−1−kreykr∣v∣cosφe(5)
有了模型的微分方程,我们可以根据李雅普诺夫第二方法设计该模型的车辆航向变化率 φ ˙ \dot{\varphi} φ˙。
李雅普诺夫第二方法:
稳定的系统能量总是不断被耗散的,李雅普诺夫通过定义一个标量函数 V ( x ) V(x) V(x) (通常能代表广义能量)来分析稳定性。这种方法的避免了直接求解方程,也没有进行近似线性化,所以也一般称之为直接法。 V ( x ) V(x) V(x)需满足:
- V ( x ) = 0 V(x)=0 V(x)=0 当且仅当 x = 0 x =0 x=0
- V ( x ) > 0 V(x)>0 V(x)>0 当且仅当 x ≠ 0 x\neq0 x=0
- V ˙ ( x ) ≤ 0 \dot{V}(x)\leq0 V˙(x)≤0 当 x ≠ 0 x \neq0 x=0
则称系统在李雅普诺夫意义下是稳定的,特别的,若 x ≠ 0 x \neq0 x=0时,有 V ˙ ( x ) < 0 \dot{V}(x)<0 V˙(x)<0,则系统是渐进稳定的。
这里我们比较关心的就是横向误差 e y e_y ey和 φ e \varphi_e φe,期望他们随着时间的增长逐渐收敛于0,我们可以定义李雅普诺夫函数形式如下:
V ( e y , φ e ) = 1 2 e y 2 + 1 2 k e φ e 2 (6) V(e_y,\varphi_e)=\frac{1}{2}e_y^2+\frac{1}{2k_e}\varphi_e^2 \tag{6} V(ey,φe)=21ey2+2ke1φe2(6)
其中 k e > 0 k_e>0 ke>0。
为了使 ( e y , φ e ) (e_y,\varphi_e) (ey,φe)在平衡点 ( 0 , 0 ) (0,0) (0,0)处稳定,根据李雅普诺夫第二方法的稳定判据, V ( x ) V(x) V(x)需满足:
- V ( e y , φ e ) = 0 V(e_y,\varphi_e)=0 V(ey,φe)=0 当且仅当 e y = 0 , φ e = 0 e_y=0,\varphi_e =0 ey=0,φe=0
- V ( e y , φ e ) > 0 V(e_y,\varphi_e)>0 V(ey,φe)>0 当且仅当 e y ≠ 0 , φ e ≠ 0 e_y\neq0,\varphi_e\neq0 ey=0,φe=0
- V ˙ ( e y , φ e ) ≤ 0 \dot{V}(e_y,\varphi_e)\leq0 V˙(ey,φe)≤0 当 e y ≠ 0 , φ e ≠ 0 e_y\neq0,\varphi_e\neq0 ey=0,φe=0
对于1、2两条,我们选取的李亚普函数 V ( e y , φ e ) V(e_y,\varphi_e) V(ey,φe)显然满足。所以满足李雅普诺夫第二方法的前两条。
对于 V ˙ ( e y , φ e ) \dot{V}(e_y,\varphi_e) V˙(ey,φe)我们结合(5)可得
V ˙ ( e y , φ e ) = e y e y ˙ + 1 k e φ e φ e ˙ = e y ∣ v ⃗ ∣ s i n φ e + 1 k e φ e ( φ ˙ − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y ) (7) \begin{aligned} \dot{V}(e_y,\varphi_e) &=e_y\dot{e_y}+\frac{1}{k_e}\varphi_e \dot{\varphi_e}\\ &=e_y|\vec{v}| sin{\varphi_e}+ \frac{1}{k_e}\varphi_e(\dot{\varphi}-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}) \end{aligned} \tag{7} V˙(ey,φe)=eyey˙+ke1φeφe˙=ey∣v∣sinφe+ke1φe(φ˙−1−kreykr∣v∣cosφe)(7)
令 V ˙ ( e y , φ e ) = 0 \dot{V}(e_y,\varphi_e)=0 V˙(ey,φe)=0,结合(7)式可得
e y ∣ v ⃗ ∣ s i n φ e + 1 k e φ e ( φ ˙ − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y ) = 0 k e e y ∣ v ⃗ ∣ s i n φ e φ e + φ ˙ − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y = 0 (8) \begin{aligned} e_y|\vec{v}| sin{\varphi_e}+ \frac{1}{k_e}\varphi_e(\dot{\varphi}-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y})&=0\\ k_ee_y|\vec{v}| \frac{sin{\varphi_e}}{\varphi_e}+ \dot{\varphi}-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}&=0 \end{aligned} \tag{8} ey∣v∣sinφe+ke1φe(φ˙−1−kreykr∣v∣cosφe)keey∣v∣φesinφe+φ˙−1−kreykr∣v∣cosφe=0=0(8)
由上式可以得到零界航向变化率 φ 0 ˙ \dot{\varphi_0} φ0˙等于
φ 0 ˙ = k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y − k e e y ∣ v ⃗ ∣ s i n φ e φ e (9) \dot{\varphi_0}=\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}-k_ee_y|\vec{v}| \frac{sin{\varphi_e}}{\varphi_e} \tag{9} φ0˙=1−kreykr∣v∣cosφe−keey∣v∣φesinφe(9)
为了使 V ˙ ( e y , φ e ) \dot{V}(e_y,\varphi_e) V˙(ey,φe)满足要求3,我们可以设计一个调节函数 g ( e y , φ e ) = k φ ∣ v ⃗ ∣ φ e > 0 g(e_y,\varphi_e) = k_\varphi |\vec{v}|\varphi_e>0 g(ey,φe)=kφ∣v∣φe>0,其中 k φ > 0 k_{\varphi}>0 kφ>0,我们可以将车辆航向的变化率 φ ˙ \dot{\varphi} φ˙设置为
φ ˙ = φ 0 ˙ − g ( e y , φ e ) = k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y − k e e y ∣ v ⃗ ∣ s i n φ e φ e − k φ ∣ v ⃗ ∣ φ e (10) \dot{\varphi}=\dot{\varphi_0}-g(e_y,\varphi_e)=\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}-k_ee_y|\vec{v}| \frac{sin{\varphi_e}}{\varphi_e}-k_\varphi |\vec{v}|\varphi_e \tag{10} φ˙=φ0˙−g(ey,φe)=1−kreykr∣v∣cosφe−keey∣v∣φesinφe−kφ∣v∣φe(10)
将(10)代入(7)得
V ˙ ( e y , φ e ) = e y ∣ v ⃗ ∣ s i n φ e + 1 k e φ e ( φ ˙ − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y ) = e y ∣ v ⃗ ∣ s i n φ e + 1 k e φ e ( k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y − k e e y ∣ v ⃗ ∣ s i n φ e φ e − k φ ∣ v ⃗ ∣ φ e − k r ∣ v ⃗ ∣ c o s φ e 1 − k r e y ) = e y ∣ v ⃗ ∣ s i n φ e + 1 k e φ e ( − k e e y ∣ v ⃗ ∣ s i n φ e φ e − k φ ∣ v ⃗ ∣ φ e ) = − k φ k e ∣ v ⃗ ∣ φ e 2 < 0 (11) \begin{aligned} \dot{V}(e_y,\varphi_e) &=e_y|\vec{v}| sin{\varphi_e}+ \frac{1}{k_e}\varphi_e(\dot{\varphi}-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y})\\ &=e_y|\vec{v}| sin{\varphi_e}+ \frac{1}{k_e}\varphi_e(\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}-k_ee_y|\vec{v}| \frac{sin{\varphi_e}}{\varphi_e}-k_\varphi |\vec{v}|\varphi_e-\frac{k_r|\vec{v}|cos{\varphi_e}}{1-k_re_y}) \\ &=e_y|\vec{v}| sin{\varphi_e}+\frac{1}{k_e}\varphi_e(-k_ee_y|\vec{v}| \frac{sin{\varphi_e}}{\varphi_e}-k_\varphi |\vec{v}|\varphi_e) \\ &=-\frac{k_\varphi}{k_e} |\vec{v}|\varphi_e^2 < 0 \end{aligned} \tag{11} V˙(ey,φe)=ey∣v∣sinφe+ke1φe(φ˙−1−kreykr∣v∣cosφe)=ey∣v∣sinφe+ke1φe(1−kreykr∣v∣cosφe−keey∣v∣φesinφe−kφ∣v∣φe−1−kreykr∣v∣cosφe)=ey∣v∣sinφe+ke1φe(−keey∣v∣φesinφe−kφ∣v∣φe)=−kekφ∣v∣φe2<0(11)
因此我们设计的公式(10)即车辆航向的变化率 φ ˙ \dot{\varphi} φ˙满足李雅普诺夫的稳定性条件。
根据前面文章介绍过的车辆运动学模型下的几何关系
t a n δ f = L R (12) tan\delta_f=\frac{L}{R} \tag{12} tanδf=RL(12)
车辆的航向变化率与车速的转弯半径关系 φ ˙ = v / R \dot{\varphi}=v/R φ˙=v/R,结合上式可得
δ f = a r c t a n φ ˙ L v (13) \delta_f=arctan\frac{\dot{\varphi}L}{v} \tag{13} δf=arctanvφ˙L(13)
3. 算法和仿真实现
rear_wheel_feedback.py
import math
import numpy as npclass C:# System configK_theta = 1.0K_e = 0.5def normalize_angle(angle):a = math.fmod(angle + np.pi, 2 * np.pi)if a < 0.0:a += (2.0 * np.pi)return a - np.pidef rear_wheel_feedback_control(vehicle, ref_path):theta_e, er, k, ind = calc_preparation(vehicle, ref_path)vr = vehicle.vdot_phi = vr * k * math.cos(theta_e) / (1.0 - k * er) - \C.K_theta * abs(vr) * theta_e - C.K_e * vr * math.sin(theta_e) * er / (theta_e + 1e-19)delta = math.atan2(vehicle.L * dot_phi, vr)return delta, ind, erdef calc_preparation(vehicle, ref_path):"""计算角度误差theta_e、横向误差er、曲率rk和索引index"""rx, ry, ref_yaw, ref_kappa = ref_path[:, 0], ref_path[:, 1], ref_path[:, 2], ref_path[:, 4]dx = [vehicle.x - icx for icx in rx]dy = [vehicle.y - icy for icy in ry]d = np.hypot(dx, dy)index = np.argmin(d)rk = ref_kappa[index]ryaw = ref_yaw[index]vec_nr = np.array([math.cos(ryaw + math.pi / 2.0),math.sin(ryaw + math.pi / 2.0)])vec_target_2_rear = np.array([vehicle.x - rx[index],vehicle.y - ry[index]])er = np.dot(vec_target_2_rear, vec_nr)theta_e = normalize_angle(vehicle.yaw - ryaw)return theta_e, er, rk, indexkinematic_bicycle_model.py
import math
import numpy as npclass Vehicle:def __init__(self,x=0.0,y=0.0,yaw=0.0,v=0.0,dt=0.1,l=3.0):self.steer = 0self.x = xself.y = yself.yaw = yawself.v = vself.dt = dtself.L = l # 轴距self.x_front = x + l * math.cos(yaw)self.y_front = y + l * math.sin(yaw)def update(self, a, delta, max_steer=np.pi):delta = np.clip(delta, -max_steer, max_steer)self.steer = deltaself.x = self.x + self.v * math.cos(self.yaw) * self.dtself.y = self.y + self.v * math.sin(self.yaw) * self.dtself.yaw = self.yaw + self.v / self.L * math.tan(delta) * self.dtself.v = self.v + a * self.dtself.x_front = self.x + self.L * math.cos(self.yaw)self.y_front = self.y + self.L * math.sin(self.yaw)class VehicleInfo:# Vehicle parameterL = 3.0 #轴距W = 2.0 #宽度LF = 3.8 #后轴中心到车头距离LB = 0.8 #后轴中心到车尾距离MAX_STEER = 0.6 # 最大前轮转角TR = 0.5 # 轮子半径TW = 0.5 # 轮子宽度WD = W #轮距LENGTH = LB + LF # 车辆长度def draw_trailer(x, y, yaw, steer, ax, vehicle_info=VehicleInfo, color='black'):vehicle_outline = np.array([[-vehicle_info.LB, vehicle_info.LF, vehicle_info.LF, -vehicle_info.LB, -vehicle_info.LB],[vehicle_info.W / 2, vehicle_info.W / 2, -vehicle_info.W / 2, -vehicle_info.W / 2, vehicle_info.W / 2]])wheel = np.array([[-vehicle_info.TR, vehicle_info.TR, vehicle_info.TR, -vehicle_info.TR, -vehicle_info.TR],[vehicle_info.TW / 2, vehicle_info.TW / 2, -vehicle_info.TW / 2, -vehicle_info.TW / 2, vehicle_info.TW / 2]])rr_wheel = wheel.copy() #右后轮rl_wheel = wheel.copy() #左后轮fr_wheel = wheel.copy() #右前轮fl_wheel = wheel.copy() #左前轮rr_wheel[1,:] += vehicle_info.WD/2rl_wheel[1,:] -= vehicle_info.WD/2#方向盘旋转rot1 = np.array([[np.cos(steer), -np.sin(steer)],[np.sin(steer), np.cos(steer)]])#yaw旋转矩阵rot2 = np.array([[np.cos(yaw), -np.sin(yaw)],[np.sin(yaw), np.cos(yaw)]])fr_wheel = np.dot(rot1, fr_wheel)fl_wheel = np.dot(rot1, fl_wheel)fr_wheel += np.array([[vehicle_info.L], [-vehicle_info.WD / 2]])fl_wheel += np.array([[vehicle_info.L], [vehicle_info.WD / 2]])fr_wheel = np.dot(rot2, fr_wheel)fr_wheel[0, :] += xfr_wheel[1, :] += yfl_wheel = np.dot(rot2, fl_wheel)fl_wheel[0, :] += xfl_wheel[1, :] += yrr_wheel = np.dot(rot2, rr_wheel)rr_wheel[0, :] += xrr_wheel[1, :] += yrl_wheel = np.dot(rot2, rl_wheel)rl_wheel[0, :] += xrl_wheel[1, :] += yvehicle_outline = np.dot(rot2, vehicle_outline)vehicle_outline[0, :] += xvehicle_outline[1, :] += yax.plot(fr_wheel[0, :], fr_wheel[1, :], color)ax.plot(rr_wheel[0, :], rr_wheel[1, :], color)ax.plot(fl_wheel[0, :], fl_wheel[1, :], color)ax.plot(rl_wheel[0, :], rl_wheel[1, :], color)ax.plot(vehicle_outline[0, :], vehicle_outline[1, :], color)ax.axis('equal')
path_generator.py
"""
路径轨迹生成器
"""import math
import numpy as npclass Path:def __init__(self):self.ref_line = self.design_reference_line()self.ref_yaw = self.cal_yaw()self.ref_s = self.cal_accumulated_s()self.ref_kappa = self.cal_kappa()def design_reference_line(self):rx, ry = [], []step_curve = 0.005 * math.pistep_line = 0.25for ix in np.arange(5, 80, step_line):rx.append(ix)ry.append(60)cx, cy, cr = 80, 45, 15theta = np.arange(math.pi/2, -math.pi/2, -step_curve)for itheta in theta:rx.append(cx + cr * math.cos(itheta))ry.append(cy + cr * math.sin(itheta))for ix in np.arange(80, 15, -step_line):rx.append(ix)ry.append(30)cx, cy, cr = 15, 15, 15theta = np.arange(math.pi/2, math.pi * 1.5, step_curve)for itheta in theta:rx.append(cx + cr * math.cos(itheta))ry.append(cy + cr * math.sin(itheta))for ix in np.arange(15, 90, step_line):rx.append(ix)ry.append(0)return np.column_stack((rx, ry))def cal_yaw(self):yaw = []for i in range(len(self.ref_line)):if i == 0:yaw.append(math.atan2(self.ref_line[i + 1, 1] - self.ref_line[i, 1],self.ref_line[i + 1, 0] - self.ref_line[i, 0]))elif i == len(self.ref_line) - 1:yaw.append(math.atan2(self.ref_line[i, 1] - self.ref_line[i - 1, 1],self.ref_line[i, 0] - self.ref_line[i - 1, 0]))else:yaw.append(math.atan2(self.ref_line[i + 1, 1] - self.ref_line[i -1, 1],self.ref_line[i + 1, 0] - self.ref_line[i - 1, 0]))return yawdef cal_accumulated_s(self):s = []for i in range(len(self.ref_line)):if i == 0:s.append(0.0)else:s.append(math.sqrt((self.ref_line[i, 0] - self.ref_line[i-1, 0]) ** 2+ (self.ref_line[i, 1] - self.ref_line[i-1, 1]) ** 2))return sdef cal_kappa(self):# 计算曲线各点的切向量dp = np.gradient(self.ref_line.T, axis=1)# 计算曲线各点的二阶导数d2p = np.gradient(dp, axis=1)# 计算曲率kappa = (d2p[0] * dp[1] - d2p[1] * dp[0]) / ((dp[0] ** 2 + dp[1] ** 2) ** (3 / 2))return kappadef get_ref_line_info(self):return self.ref_line[:, 0], self.ref_line[:, 1], self.ref_yaw, self.ref_s, self.ref_kappa
main.py
from kinematic_bicycle_model import Vehicle, VehicleInfo, draw_trailer
from rear_wheel_feedback import rear_wheel_feedback_control
from path_generator import Path
import numpy as np
import matplotlib.pyplot as plt
import imageio.v2 as imageioMAX_SIMULATION_TIME = 200.0 # 程序最大运行时间200*dtdef main():# 设置跟踪轨迹rx, ry, ref_yaw, ref_s, ref_kappa = Path().get_ref_line_info()ref_path = np.column_stack((rx, ry, ref_yaw, ref_s, ref_kappa))# 假设车辆初始位置为(5,55),航向角yaw=pi/6,速度为2m/s,时间周期dt为0.1秒vehicle = Vehicle(x=5.0,y=55.0,yaw=np.pi/6,v=2.0,dt=0.1,l=VehicleInfo.L)time = 0.0 # 初始时间target_ind = 0# 记录车辆轨迹trajectory_x = []trajectory_y = []lat_err = [] # 记录横向误差i = 0image_list = [] # 存储图片plt.figure(1)last_idx = ref_path.shape[0] - 1 # 跟踪轨迹的最后一个点的索引while MAX_SIMULATION_TIME >= time and last_idx > target_ind:time += vehicle.dt # 累加一次时间周期# rear_wheel_feedbackdelta_f, target_ind, e_y = rear_wheel_feedback_control(vehicle, ref_path)# 横向误差lat_err.append(e_y)# 更新车辆状态vehicle.update(0.0, delta_f, np.pi / 10) # 由于假设纵向匀速运动,所以加速度a=0.0trajectory_x.append(vehicle.x)trajectory_y.append(vehicle.y)# 显示动图plt.cla()plt.plot(ref_path[:, 0], ref_path[:, 1], '-.b', linewidth=1.0)draw_trailer(vehicle.x, vehicle.y, vehicle.yaw, vehicle.steer, plt)plt.plot(trajectory_x, trajectory_y, "-r", label="trajectory")plt.plot(ref_path[target_ind, 0], ref_path[target_ind, 1], "go", label="target")plt.axis("equal")plt.grid(True)plt.pause(0.001)plt.savefig("temp.png")# i += 1# if (i % 50) > 0:# image_list.append(imageio.imread("temp.png"))## imageio.mimsave("display.gif", image_list, duration=0.01)plt.figure(2)plt.subplot(2, 1, 1)plt.plot(ref_path[:, 0], ref_path[:, 1], '-.b', linewidth=1.0)plt.plot(trajectory_x, trajectory_y, 'r')plt.title("actual tracking effect")plt.subplot(2, 1, 2)plt.plot(lat_err)plt.title("lateral error")plt.show()if __name__ == '__main__':main()
运行效果:

控制效果和横向误差:

以上内容仅是个人理解,如有漏误欢迎批评指正!
文章首发公众号:iDoitnow如果喜欢话,可以关注一下
相关文章:

后轮位置反馈控制与算法仿真实现
文章目录 1. 后轮反馈控制2. 算法原理3. 算法和仿真实现 1. 后轮反馈控制 后轮反馈控制(Rear wheel feedback)算法是利用后轮中心的跟踪偏差来进行转向控制量计算的方法,属于Frenet坐标系的一个应用。通过选择合适的李雅普诺夫函数设计控制率…...
实战 vue3 使用百度编辑器ueditor
前言 在开发项目由于需求vue自带对编辑器不能满足使用,所以改为百度编辑器,但是在网上搜索发现都讲得非常乱,所以写一篇使用流程的文章 提示:以下是本篇文章正文内容,下面案例可供参考 一、下载ueditor编辑器 一个“…...

N种方法解决1(CTF)
这里遇到的问题:一开始采用的base64解码平台有问题;默认解密出的格式为GBK格式;直接复制粘贴发现无法还原图片;又尝试了其他编码的;发现只有hex格式可以保证图片正常还原; 图片是以二进制存储的࿱…...
Istio实战:Istio Kiali部署与验证
目录 前言一、Istio安装小插曲 注意事项 二、Kiali安装三、Istio测试参考资料 前言 前几天我就开始捣腾Istio。前几天在执行istioctl install --set profiledemo -y 的时候老是在第二步就报错了,开始我用的istio版本是1.6.8。 后面查看k8s与istio的版本对应关系后发…...

ASPxGridView中使用PopupEditForm表单字段联动填充
c#中devexpress的控件ASPxGridView中使用PopupEditForm表单字段联动填充 //选择项目名称,自动填充项目编号 <Columns><dx:GridViewDataTextColumn FieldName"id" ReadOnly"True" VisibleIndex"0" Visible"False"…...
基于Pytorch的猫狗图片分类【深度学习CNN】
猫狗分类来源于Kaggle上的一个入门竞赛——Dogs vs Cats。为了加深对CNN的理解,基于Pytorch复现了LeNet,AlexNet,ResNet等经典CNN模型,源代码放在GitHub上,地址传送点击此处。项目大纲如下: 文章目录 一、问题描述二、数据集处理…...
flutter sliver 多种滚动组合开发指南
flutter sliver 多种滚动组合开发指南 视频 https://youtu.be/4mho1kZ_YQU https://www.bilibili.com/video/BV1WW4y1d7ZC/ 前言 有不少同学工作中遇到需要把几个不同滚动行为组件(顶部 appBar、内容固定块、tabBar 切换、tabBarView视图、自适应高度、横向滚动&a…...
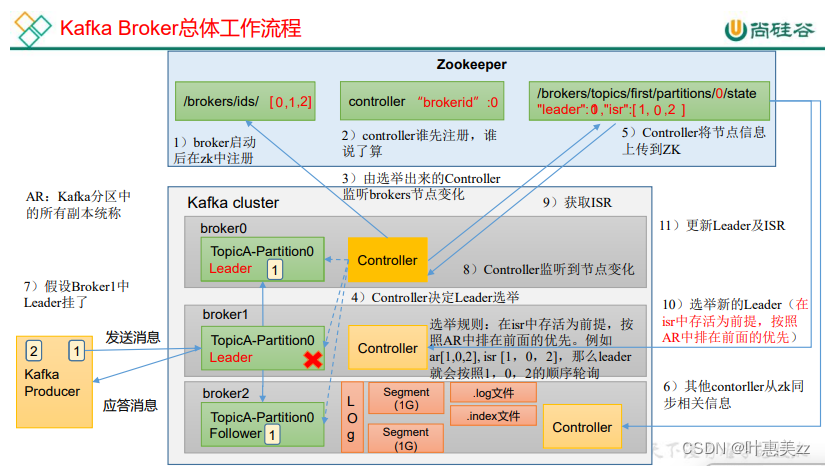
kafka生产者2
1.数据可靠 • 0:生产者发送过来的数据,不需要等数据落盘应答。 风险:leader挂了之后,follower还没有收到消息。。。。 • 1:生产者发送过来的数据,Leader收到数据后应答。 风险:leader应答…...

【LNMP】云导航项目部署及环境搭建(复杂)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、项目介绍1.1项目环境架构LNMP1.2项目代码说明 二、项目环境搭建2.1 Nginx安装2.2 php安装2.3 nginx配置和php配置2.3.1 修改nginx文件2.3.2 修改vim /etc/p…...

nginx之状态页 日志分割 自定义图表 证书
5.1 网页的状态页 基于nginx 模块 ngx_http_stub_status_module 实现,在编译安装nginx的时候需要添加编译参数 --with-http_stub_status_module,否则配置完成之后监测会是提示语法错误注意: 状态页显示的是整个服务器的状态,而非虚拟主机的状态 server{…...
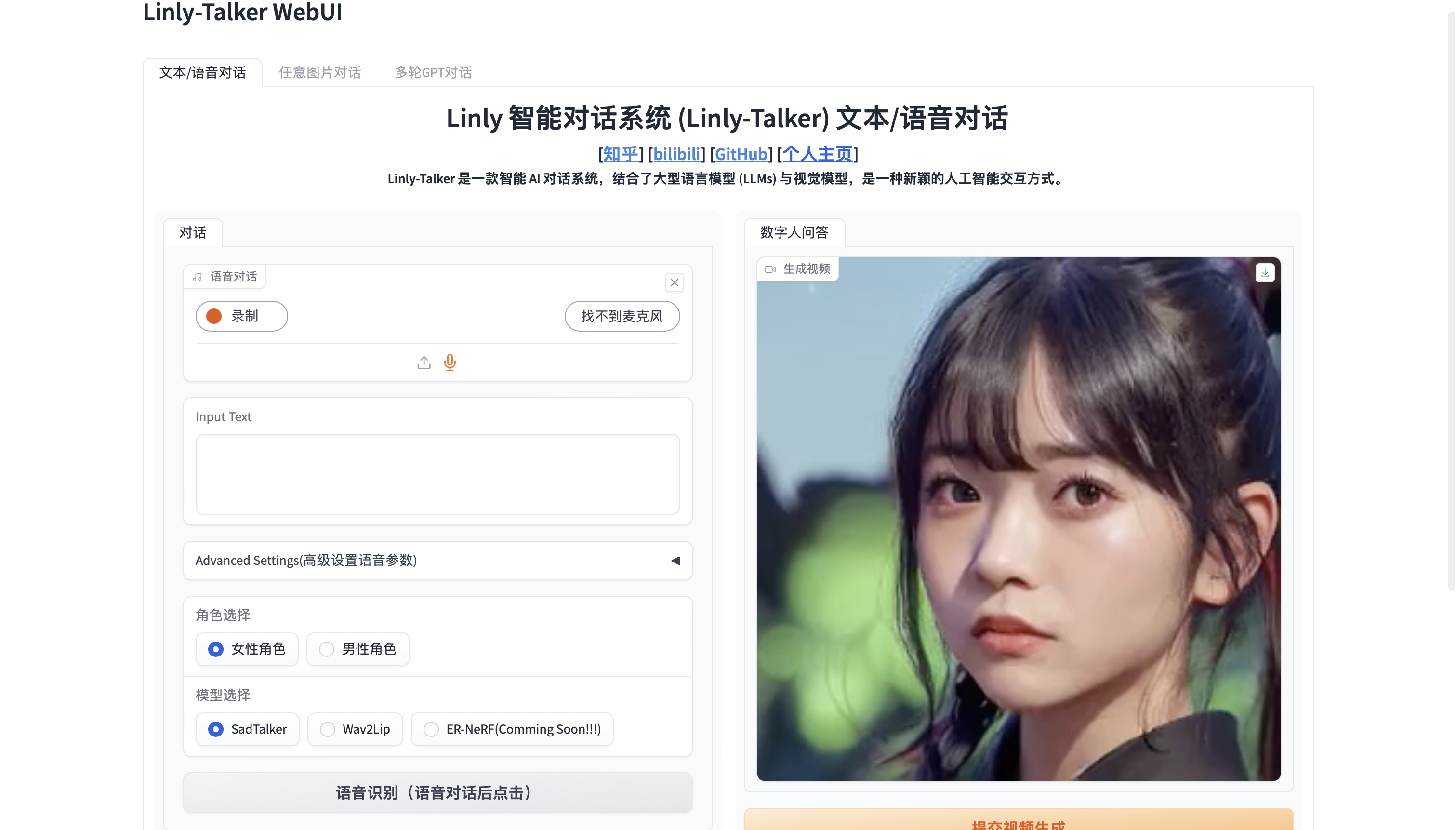
数字人的未来:数字人对话系统 Linly-Talker + 克隆语音 GPT-SoVITS
🚀数字人的未来:数字人对话系统 Linly-Talker 克隆语音 GPT-SoVITS https://github.com/Kedreamix/Linly-Talker 2023.12 更新 📆 用户可以上传任意图片进行对话 2024.01 更新 📆 令人兴奋的消息!我现在已经将强…...
SpringMVC 学习(五)之域对象
目录 1 域对象介绍 2 向 request 域对象共享数据 2.1 通过 ServletAPI (HttpServletRequest) 向 request 域对象共享数据 2.2 通过 ModelAndView 向 request 域对象共享数据 2.3 通过 Model 向 request 域对象共享数据 2.4 通过 map 向 request 域对象共享数据 2.5 通过…...
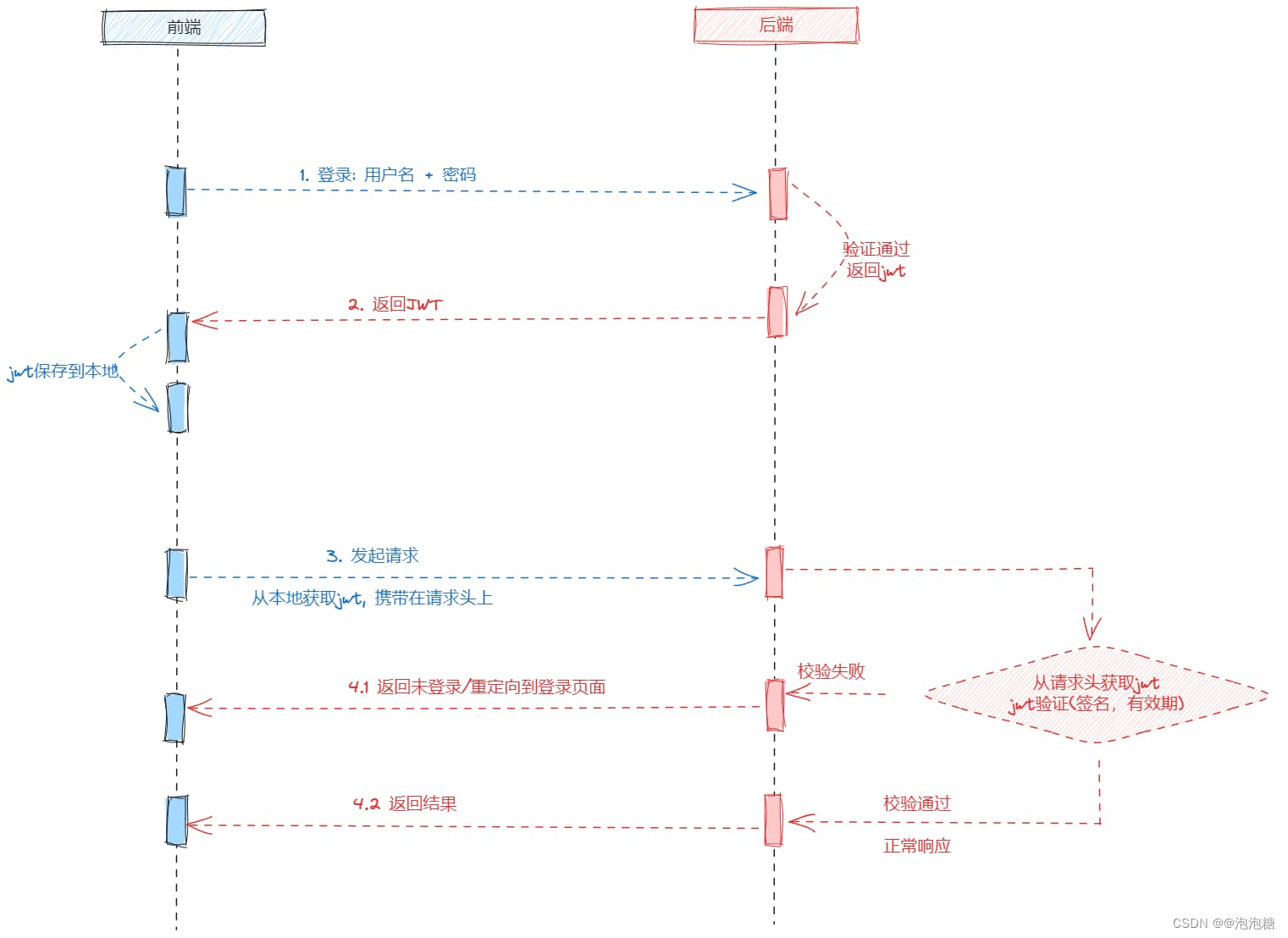
✅技术社区项目—JWT身份验证
通用的JWT鉴权方案 JWT鉴权流程 基本流程分三步: ● 用户登录成功之后,后端将生成的jwt返回给前端,然后前端将其保存在本地缓存; ● 之后前端与后端的交互时,都将iwt放在请求头中,比如可以将其放在Http的身份认证的请求头 Author…...
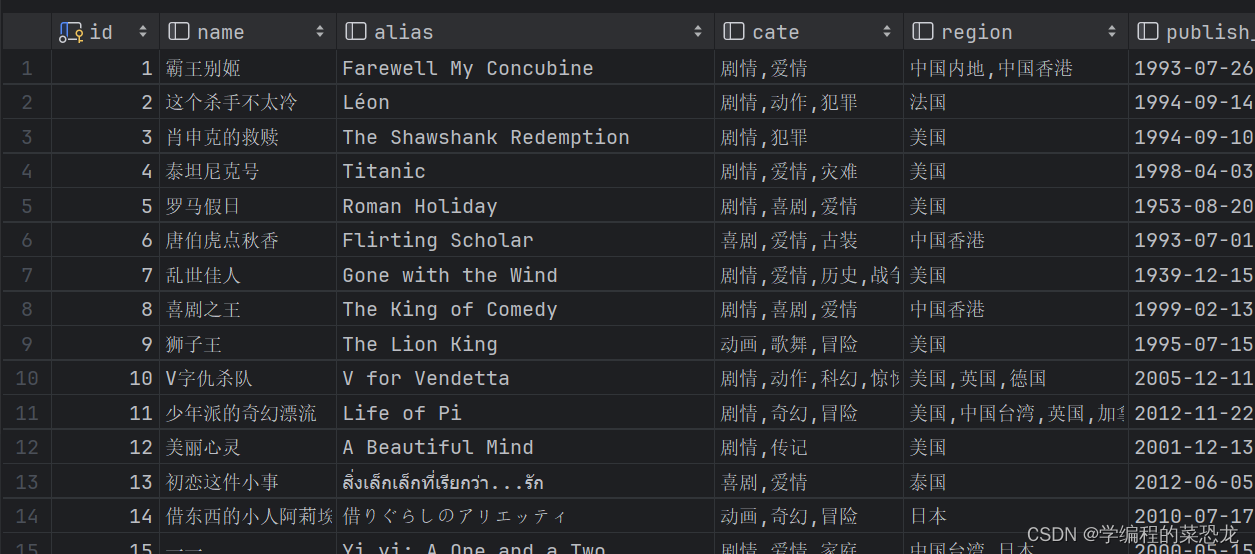
5.2 Ajax 数据爬取实战
目录 1. 实战内容 2、Ajax 分析 3、爬取内容 4、存入MySQL 数据库 4.1 创建相关表 4.2 数据插入表中 5、总代码与结果 1. 实战内容 爬取Scrape | Movie的所有电影详情页的电影名、类别、时长、上映地及时间、简介、评分,并将这些内容存入MySQL数据库中。 2、…...
)
276.【华为OD机试真题】矩阵匹配(二分法—JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-矩阵匹配二.解题思路三.题解代码Python题解代码…...
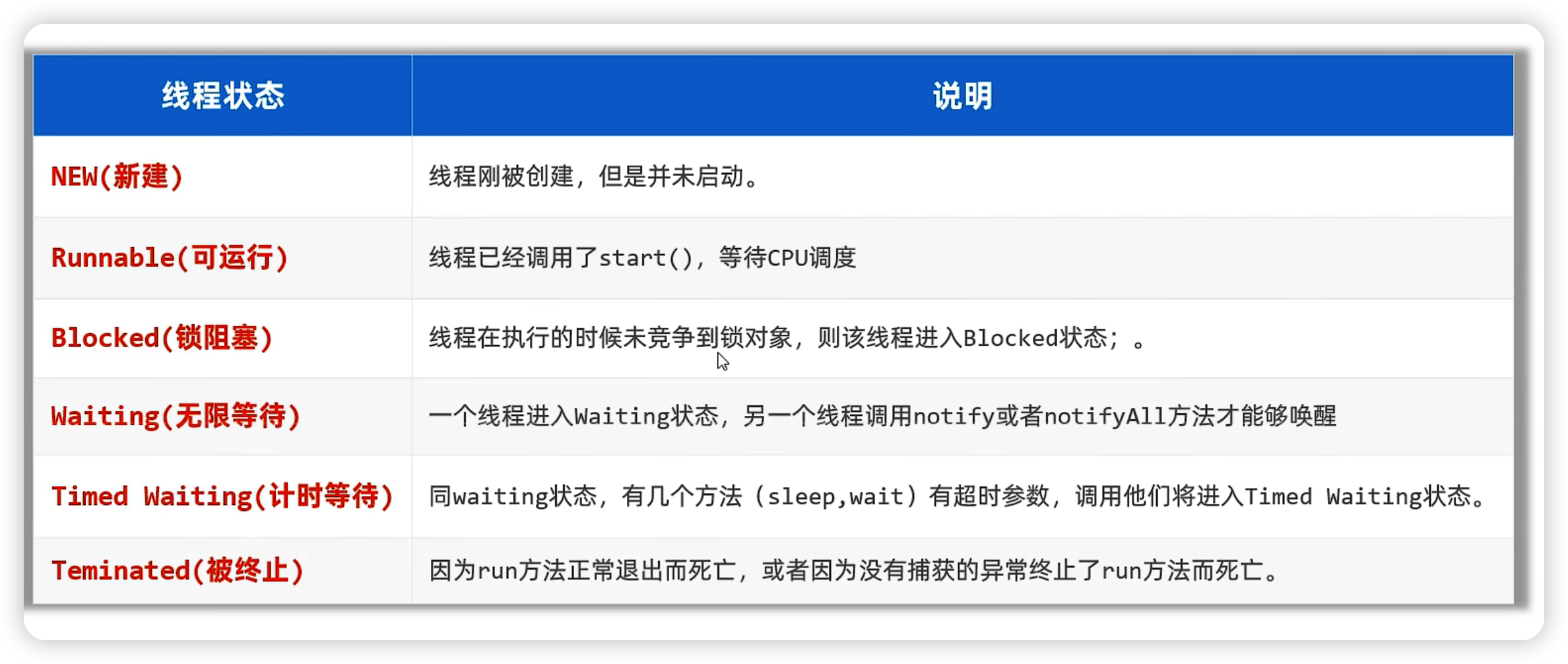
java——多线程基础
目录 线程的概述多线程的创建方式一:继承Thread类方式二:实现Runnable接口方式三:利用Callable接口、FutureTask类来实现。Thread常用的方法 线程安全问题线程安全问题概述线程安全问题案例取钱案例描述模拟代码如下:执行结果 线程…...

Python服务器监测测试策略与工具:确保应用的高可用性!
在构建高可用性的应用程序时,服务器监测测试是至关重要的一环。Python作为一种强大的编程语言,提供了丰富的工具和库来帮助我们进行服务器监测测试。本文将介绍一些关键的策略和工具,帮助你确保应用的高可用性。 1. 监测策略的制定ÿ…...
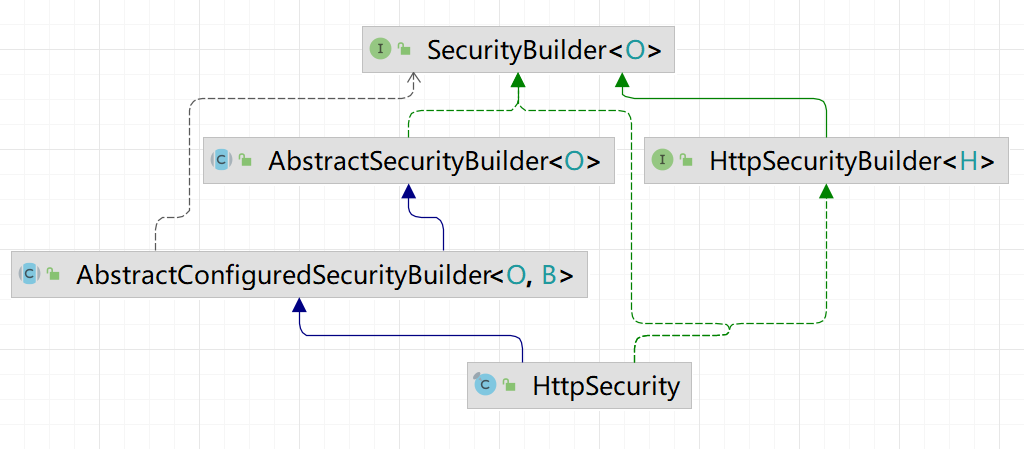
Spring Security源码学习
Spring Security本质是一个过滤器链 过滤器链本质是责任链设计模型 1. HttpSecurity 【第五篇】深入理解HttpSecurity的设计-腾讯云开发者社区-腾讯云 在以前spring security也是采用xml配置的方式,在<http>标签中配置http请求相关的配置,如用户…...

大数据面试总结三
1、hdfs作为分布式存储系统,底层的实现的方式(可能不正确) 1、底层是一个分布式存储的,底层会将数据进行切分多个block块(128M),并存储在不同的节点上面,这种分布式方式有助于提高数…...

AI赚钱套路总结和教程
最近李一舟和Sora 很火,作为第一批使用Sora赚钱的男人,一个清华学美术的跟人讲AI,信的人太多了,钱太好赚了。3年时间,李一舟仅通过卖课就赚了1.75亿元,其中《每个人的人工智能课》收入2786万元,…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
