【蓝桥杯集训·周赛】AcWing 第93场周赛
文章目录
- 第一题 AcWing 4867. 整除数
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第二题 AcWing 4868. 数字替换
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第三题 AcWing 4869. 异或值
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
第一题 AcWing 4867. 整除数
一、题目
1、原题链接
4867. 整除数
2、题目描述
给定两个整数 n,k,请你找到 大于 n 且能被 k 整除的最小整数 x。
输入格式*
共一行,包含两个整数 n,k。
输出格式
输出大于 n 且能被 k 整除的最小整数 x。
数据范围
前 4 个测试点满足 1≤n,k≤100。
所有测试点满足 1≤n,k≤109。输入样例1:
5 3输出样例1:
6输入样例2:
25 13输出样例2:
26输入样例3:
26 13输出样例3:
39
二、解题报告
1、思路分析
我的思路
求出当前的n已经是k的多少倍(即计算n/k),然后在这个倍数的基础上向后枚举,直到满足条件,退出循环,输出答案即可。
y总思路
思路来源:y总讲解视频
y总yyds
(1)分两种情况:如果当前数是k的倍数和当前数不是k的倍数。
(2)如果当前数是k的倍数,则答案应为(n/k+1)*k。
(4)如果当前数不是k的倍数,则答案也为(n/k+1)*k。
(4)所以,直接输出(n/k+1)*k即为答案。
2、时间复杂度
时间复杂度为O(1)
3、代码详解
我的思路的代码
#include <iostream>
using namespace std;
int n,k;
int main(){scanf("%d%d",&n,&k);int t=n/k;while(1){if(t*k>n){printf("%d",t*k);break;}t++;}return 0;
}
y总思路的代码
#include <iostream>
using namespace std;
int n,k;
int main(){scanf("%d%d",&n,&k);int t=n/k;cout<<(t+1)*k;return 0;
}
第二题 AcWing 4868. 数字替换
一、题目
1、原题链接
4868. 数字替换
2、题目描述
给定两个整数 n,x。
你可以对 x 进行任意次以下操作:
- 选择 x 的一位数字 y,将 x 替换为
x * y。请你计算通过使用上述操作,将 x 变为一个 n 位数字(不含前导 0),所需要的最少操作次数。
例如,当 n=3,x=2 时,对 2 进行如下 4 次操作,即可使其变为 3 位数字:
- 将 2 替换为 2×2=4。
- 将 4 替换为 4×4=16。
- 将 16 替换为 16×6=96。
- 将 96 替换为 96×9=864。
输入格式
共一行,包含两个整数 n,x。
输出格式
一个整数,表示将 x 变为一个 n 位数字,所需要的最少操作次数。
如果无解,则输出
-1。数据范围
所有测试点满足 2≤n≤19,1≤x<10n−1。
输入样例1:
2 1输出样例1:
-1输入样例2:
3 2输出样例2:
4输入样例3:
13 42输出样例3:
12
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)利用dfs进行搜索,注意剪枝和优化。
(2)搜索顺序优化:如果需要快速增加x的位数,则乘的数应该越大越好,所以可以从从大到小来枚举是否可以乘(9~0)中的在x中出现过的数。
(3)剪枝:如果我们当前搜索的分枝中,当前已经的操作次数+还至少需要操作的次数(也就是还需要扩大的位数,因为每次操作最多只能扩大一位)>=当前已收获的最优答案,则该分枝一定不如已收获的答案最优,没必要继续搜索,直接回溯即可。
(4)利用上述剪枝与优化方法,进行深搜即可。
2、时间复杂度
时间复杂度为O(nh)(h为深度,n为每个点的分枝数)
3、代码详解
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL; //注意数据范围,用long long存
int n;
LL x;
int ans=0x3f3f3f3f;
void dfs(LL x,int sum){ //sum代表当前操作次数bool st[10]={0}; //st[]存储0~9是否在x的某一位数字出现过int cnt=0; //记录x一共有多少位数LL k=x; //为避免后续统计x一共有多少位数时改变x的值,将k暂存x的值,用k来完成后续统计//统计x一共有多少位数,已经0~9是否出现过while(k){cnt++; st[k%10]=true;k/=10;}if(sum+n-cnt>=ans) return ; //如果当前操作次数+相差的位数比已经搜到的总操作次数要大或相等,则说明该分枝的情况一定不如已收获的结果最优,没有必要向下搜索,直接回溯即可if(cnt==n){ //搜到一组答案,记录结果 ans=min(ans,sum);return ;}//从大到小枚举,看是否在x中出现过,如果出现过继续向下搜索for(int i=9;i>=2;i--){ //相乘0或1只会让结果更差,不会得到最优解,没必要枚举if(st[i])dfs(x*i,sum+1); //自带回溯}
}
int main(){cin>>n>>x;dfs(x,0); //记得调用if(ans==0x3f3f3f3f) cout<<-1;else cout<<ans;return 0;
}
第三题 AcWing 4869. 异或值
一、题目
1、原题链接
4869. 异或值
2、题目描述
给定一个长度为 n 的整数序列 a1,a2,…,an。
请你找到一个非负整数 X,使得 max1≤i≤n{ai⊕X} 的值尽可能小,其中 ⊕ 表示按位异或。
输出 max1≤i≤n{ai⊕X} 的最小可能值。
输入格式
第一行包含整数 n。
第二行包含 n 个整数 a1,a2,…,an。
输出格式
一个整数,表示 max1≤i≤n{ai⊕X} 的最小可能值。
数据范围
前 3 个测试点满足 1≤n≤3。
所有测试点满足 1≤n≤105,0≤ai≤230−1。输入样例1:
3 1 2 3输出样例1:
2输入样例2:
2 1 5输出样例2:
4
二、解题报告
1、思路分析
思路来源:4869. 异或值
y总yyds
(1)首先将所有的数按其二进制的形式从最高位到最低位(Tire树中左分枝存储0,右分枝存储1),由根向结点延伸依次插入Tire树中。
(2)从最高位到最低位依次来确定x的值,x的最高位可能取0或1,针对两个分枝,递归地去求解左右子树确定的最大值的最小值(即dp[l]和dp[r]):
- 如果
x最高位为0,走0分枝所求应为dp[l];如果走1分枝,所求应为dp[r]+最高位^1<<d(最高位异或值为1,所以需要加上该位代表的数,d为最高位的位置)。这两个分枝的最大值即为左子树的最大值的最小值。 - 如果x的最高位为
1,走0分枝所求应为dp[l]+最高位^1<<d(最高位异或值为1所以需要加上该位代表的数,d为最高位的位置);如果走0分枝,所求应为dp[r]。这两个分枝的最大值即为右子树的最大值的最小值。
然后求解完毕后,因为求的是最小值,所以直接将两种情况求出的结果取一个最小值,即为答案。
2、时间复杂度
时间复杂度为O(nlogn)
3、代码详解
#include <iostream>
#include <algorithm>
using namespace std;
const int N=3000010; //Tire数总结点数,总共10^5个数,每个数30位,所以需要开到大于3*10^6
int son[N][2],idx;
int n;
//Tire树按二进制形式从高位到低位按从根到结点的顺序插入每个数
void insert(int n){int p=0;for(int i=29;i>=0;i--){int u=n>>i&1;if(!son[p][u]) son[p][u]=++idx;p=son[p][u];}
}
int dfs(int u,int d){ //u表示结点,d表示高度(最高位的位置)if(d==-1) return 0; //已经遍历完叶结点,回溯int dp[2];//求子树的确定的最大值的最小值for(int i=0;i<2;i++){int p=son[u][i];if(p) dp[i]=dfs(p,d-1); //递归求子树确定的最大值的最小值else dp[i]=-1; //如果当前结点不存在返回-1}int ans=2e9;for(int i=0;i<2;i++){ //枚举x最高位int t=0;//枚举左右子树for(int j=0;j<2;j++){if(dp[j]!=-1)t=max(t,dp[j]+((i^j)<<d)); //对于左右子树的子树,需要左右子树的子树中分枝的最大值,即为该左/右子树确定的最大值的最小值}ans=min(ans,t); //在左右子树确定的值中取最小值即为答案}return ans;
}
int main(){cin>>n;while(n--){int a;cin>>a;insert(a);}cout<<dfs(0,29);return 0;
}
相关文章:

【蓝桥杯集训·周赛】AcWing 第93场周赛
文章目录第一题 AcWing 4867. 整除数一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4868. 数字替换一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4869. 异或值一、题目1、原题…...
蓝桥杯-刷题统计
蓝桥杯-刷题统计1、问题描述2、解题思路3、代码实现3.1 方案一:累加方法(超时)3.2 方案二1、问题描述 小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目, 周六和周日每天做 b 道题目。请你帮小明计算, 按照计划他将在 第几天实现做题数…...

Linux入门教程||Linux Shell 变量|| Shell 传递参数
Shell 变量 定义变量时,变量名不加美元符号($,PHP语言中变量需要),如: your_name"w3cschool.cn"注意,变量名和等号之间不能有空格,这可能和你熟悉的所有编程语言都不一…...
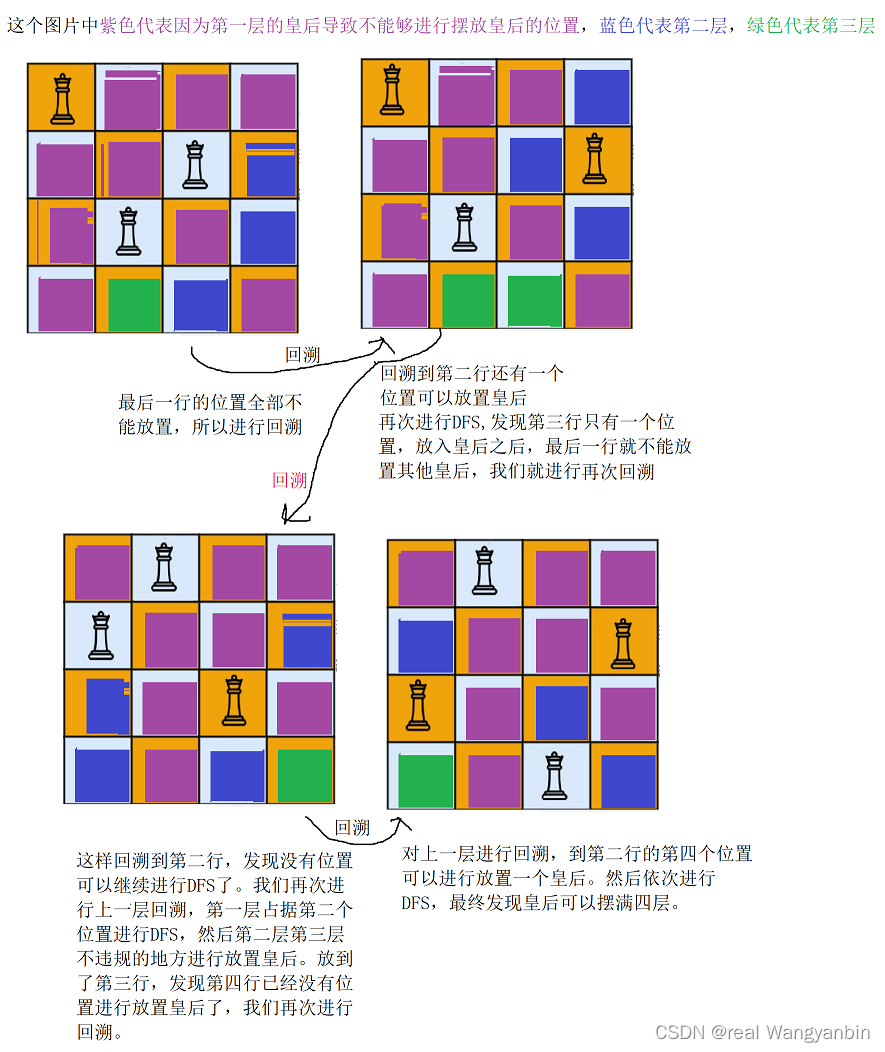
[算法和数据结构]--回溯算法之DFS初识
回溯算法——DFSDFS介绍(Depth First Search)DFS经典题目1. 员工的重要性2. 图像渲染3.被围绕的区域4.岛屿数量5. 电话号码的字母组合6.数字组合7. 活字印刷8. N皇后DFS介绍(Depth First Search) 回溯法(back tracking)(探索与回溯法&#x…...
【LeetCode每日一题】——680.验证回文串 II
文章目录一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【解题思路】七【题目提示】八【时间频度】九【代码实现】十【提交结果】一【题目类别】 贪心算法 二【题目难度】 简单 三【题目编号】 680.验证回文串 II 四【题目描述】 给你一个字…...

【C语言进阶:指针的进阶】你真分得清sizeof和strlen?
本章重点内容: 字符指针指针数组数组指针数组传参和指针传参函数指针函数指针数组指向函数指针数组的指针回调函数指针和数组面试题的解析这篇博客 FLASH 将带大家一起来练习一些容易让人凌乱的题目,通过这些题目来进一步加深和巩固对数组,指…...
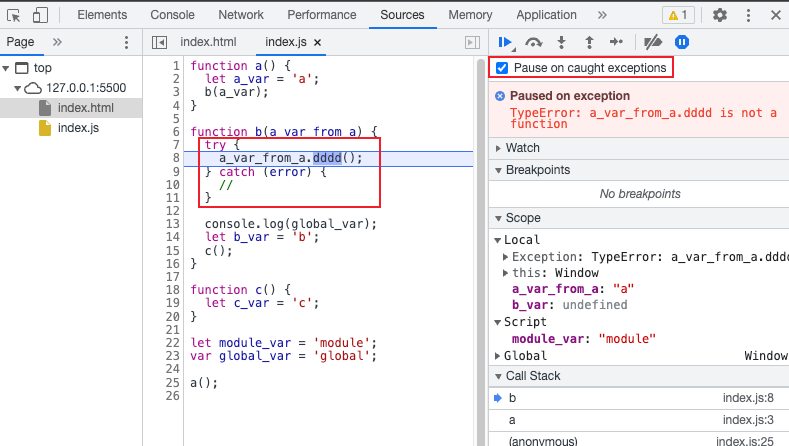
【前端必看】极大提高开发效率的网页 JS 调试技巧
大家好,我是前端西瓜哥。本文讲解如何使用浏览器提供的工具进行 JS 代码的断点调试。 debugger 在代码中需要打断点的地方,加上 debugger,表示一个断点。浏览器代码执行到该位置时,会停下来,进入调试模式。 示例代码…...

【春招面经】视源股份前端一面
前言 本次主要记录一下视源股份CVTE前端一面 (3.3下午4点15) 文章目录前言本次主要记录一下视源股份CVTE前端一面 (3.3下午4点15)问题总结介绍一下项目的来源以及做这个项目的初衷一直监听滚动,有没有对性能产生影响&a…...
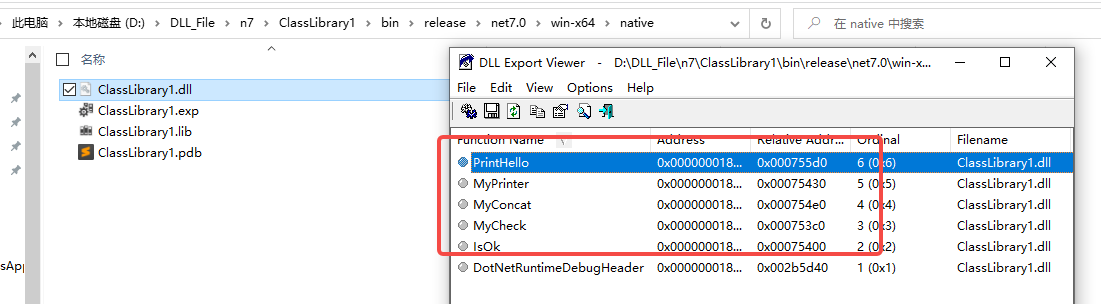
插件化开发入门
一、背景顾名思义,插件化开发就是将某个功能代码封装为一个插件模块,通过插件中心的配置来下载、激活、禁用、或者卸载,主程序无需再次重启即可获取新的功能,从而实现快速集成。当然,实现这样的效果,必须遵…...

tftp、nfs 服务器环境搭建
目录 一、认识 tftp、nfs 1、什么是 tftp? 2、什么是 nfs? 3、tftp 和 nfs 的区别 二、tftp的安装 1、安装 tftp 服务端 2、配置 tftp 3、启动 tftp 服务 三、nfs 的安装 1、安装 nfs 服务端 2、配置 nfs 3、启动 nfs 服务 一、认识 tftp、…...
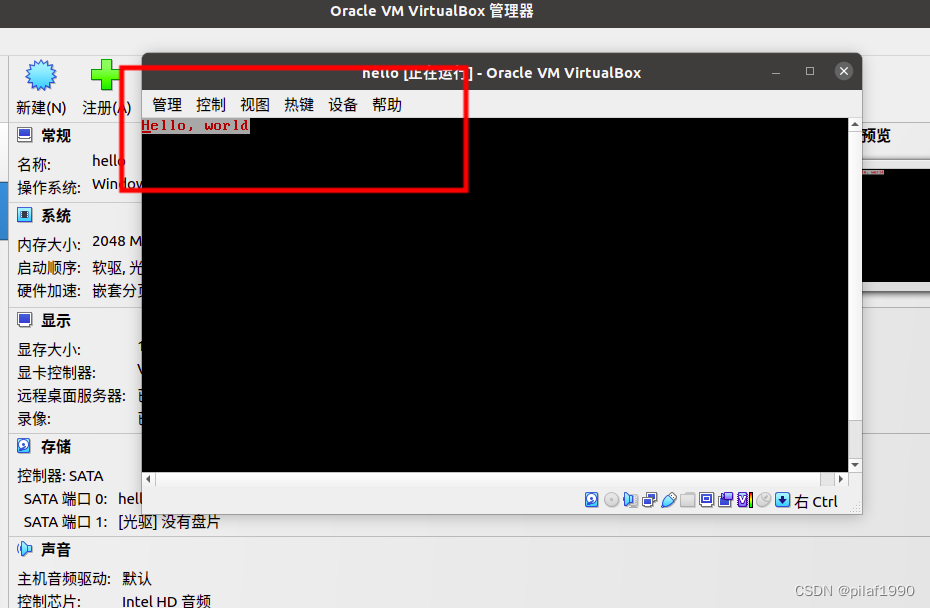
汇编系列03-不借助操作系统输出Hello World
每天进步一点点,加油! 上一节,我们通过汇编指令,借助操作系统的系统调用实现了向标准输出打印Hello world。这一节我们打算绕过操作系统,直接在显示屏幕上打印Hello world。 计算机的启动过程 当我们给计算机加电启…...

TPU编程竞赛系列|算能赛道冠军SO-FAST团队获第十届CCF BDCI总决赛特等奖!
近日,第十届中国计算机学会(CCF)大数据与计算智能大赛总决赛暨颁奖典礼在苏州顺利落幕,算能赛道的冠军队伍SO-FAST从2万余支队伍中脱颖而出,获得了所有赛道综合评比特等奖! 本届CCF大赛吸引了来自全国的2万…...
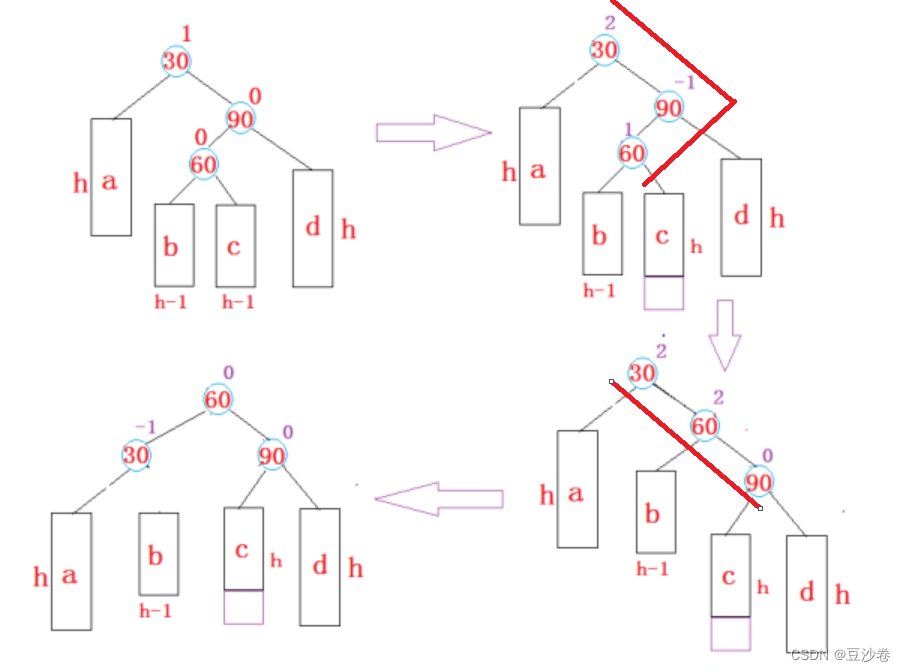
【C++】AVL树,平衡二叉树详细解析
文章目录前言1.AVL树的概念2.AVL树节点的定义3.AVL树的插入4.AVL树的旋转左单旋右单旋左右双旋右左双旋AVL树的验证AVL树的删除AVL树的性能前言 前面对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是࿱…...
C/C++开发,无可避免的多线程(篇四).线程与函数的奇妙碰撞
一、函数、函数指针及函数对象 1.1 函数 函数(function)是把一个语句序列(函数体, function body)关联到一个名字和零或更多个函数形参(function parameter)的列表的 C 实体,可以通过返回或者抛…...

elisp简单实例: taglist
从vim 转到emacs 下,一直为缺少vim 中的tablist 插件而感到失落. 从网上得到的一个emacs中的taglist, 它的功能很简陋,而且没有任何说明, 把它做为elisp的简单实例,供初学者入门倒不错,我给它加了很多注释,帮助理解, 说实话,感觉这百行代码还是挺有深度的,慢慢体会,调试才会有收…...
-认知服务(3))
Azure AI基础到实战(C#2022)-认知服务(3)
目录 OpenFileDialog 类上一节代码的API剖析ComputerVisionClientExtensions.ReadAsync MethodReadHeaders ClassReadHeaders.OperationLocation Property探索ReadHeaders加上调试代码可用于 Azure 认知服务的身份验证标头使用单服务订阅密钥进行身份验证使用多服务订阅密钥进行…...
aws apigateway 使用restapi集成lambda
参考资料 代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/api-gateway-create-api-as-simple-proxy-for-lambda.html非代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/getting-started-…...
HTML基础
HTML 基础 文章目录HTML 基础列表标签无序列表有序列表自定义列表表格标签表格基本标签表格基本结构表格完整结构:合并行和合并列表单标签input 系列标签属性标签text 标签radio 标签 单选框file 标签 文件选择button 标签 按钮input系列标签总结button按钮标签sele…...

ThreadPoolExecutor参数 keepAliveTime allowCoreThreadTimeOut
/*** Timeout in nanoseconds for idle threads waiting for work.* Threads use this timeout when there are more than corePoolSize* present or if allowCoreThreadTimeOut. Otherwise they wait* forever for new work.*/ private volatile long keepAliveTime;等待工作的…...

什么是Hibernate框架?
简单介绍:Hibernate框架是当今主流的java持久层框架之一,是一个开放源码的ORM(Object Relational Mapping,对象关系映射)框架,它对JDBC进行了轻量级的封装,使得JAVA开发人员可以使用面向对象的编…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
