代码随想录算法训练营第四一天 | 背包问题
目录
- 背包问题
- 01背包
- 二维dp数组01背包
- 一维 dp 数组(滚动数组)
- 分割等和子集
背包问题
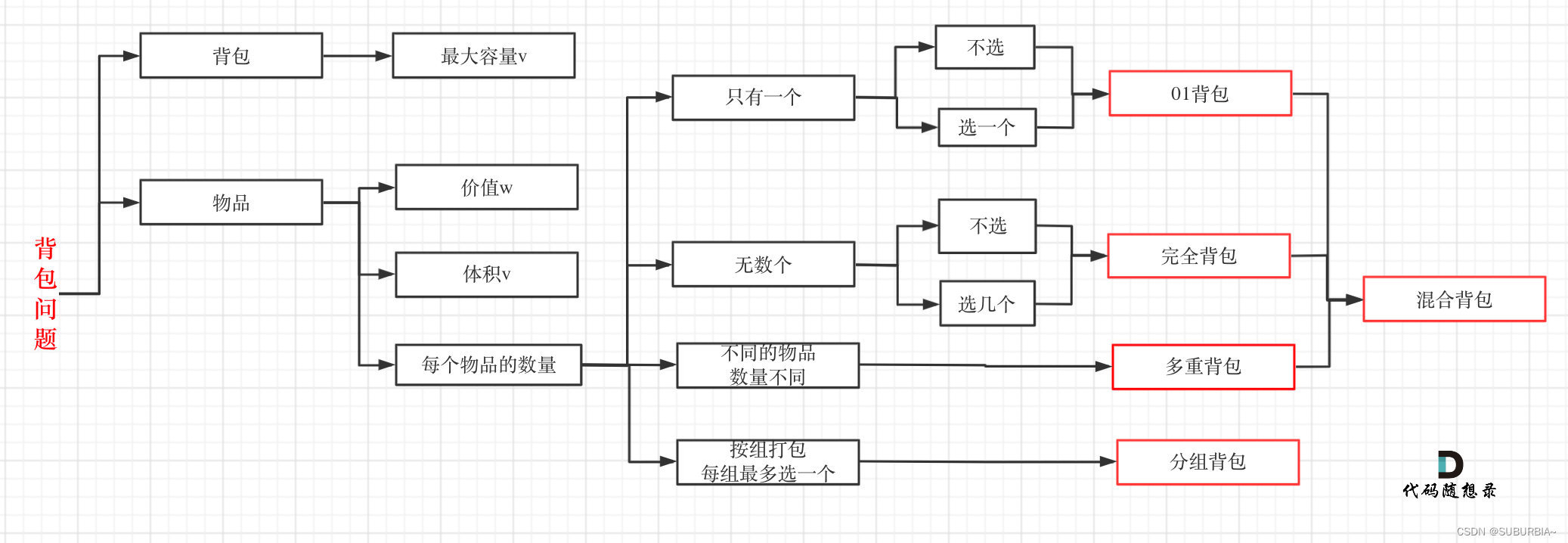
01背包
有n件物品和一个最多能背重量为 w 的背包,第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
暴力的解法: 回溯,时间复杂度就是 o ( 2 n ) o(2^n) o(2n),这里的n表示物品数量。
暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化。
- 举例: 背包最大重量为4。
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
二维dp数组01背包
-
dp数组:dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
-
递推公式:两个方向推出来dp[i][j]
- 不放物品 i :由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递推公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
-
初始化
如果背包容量 j 为 0 的话,dp[i][0], 无论选取哪些物品,背包价值总和一定为0。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
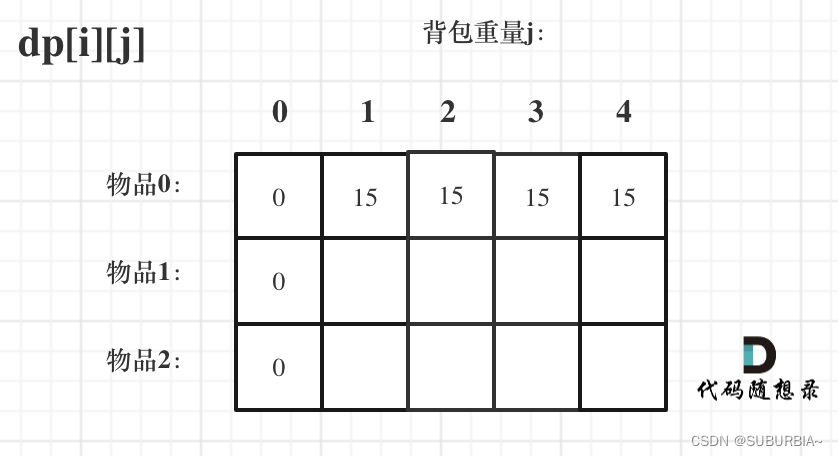
-
遍历顺序
两个遍历维度: 物品与背包重量
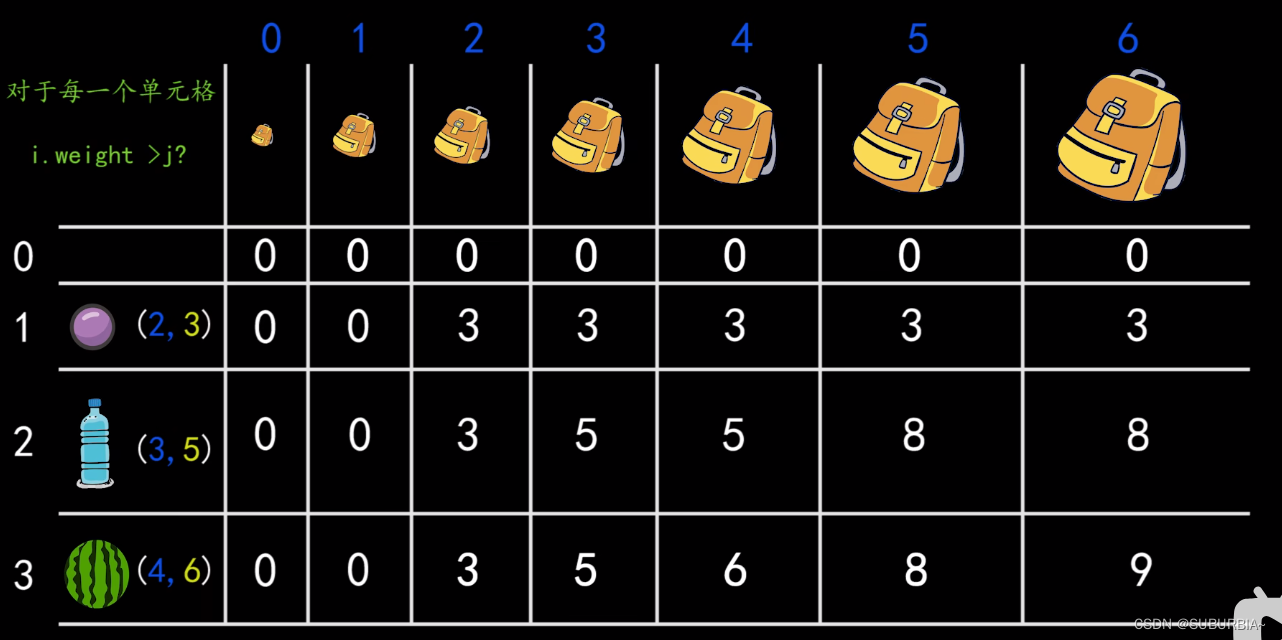
先遍历物品,再遍历背包的过程如图所示:
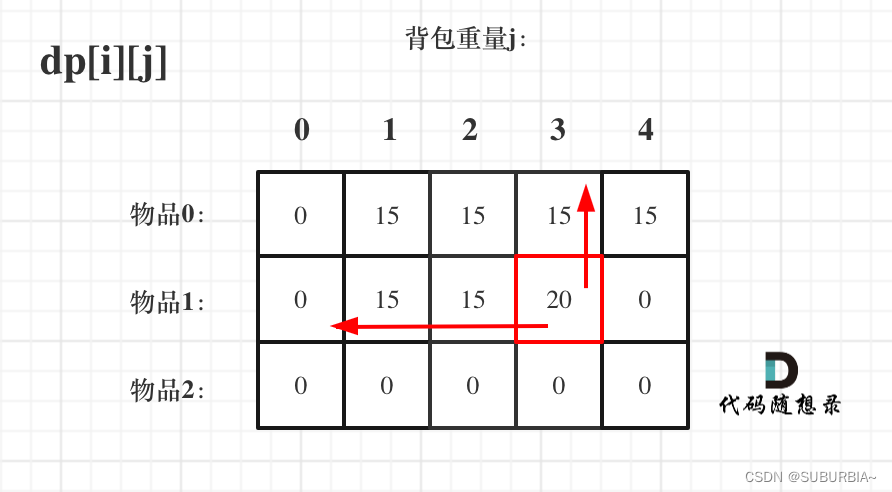
先遍历背包,再遍历物品呢,如图:
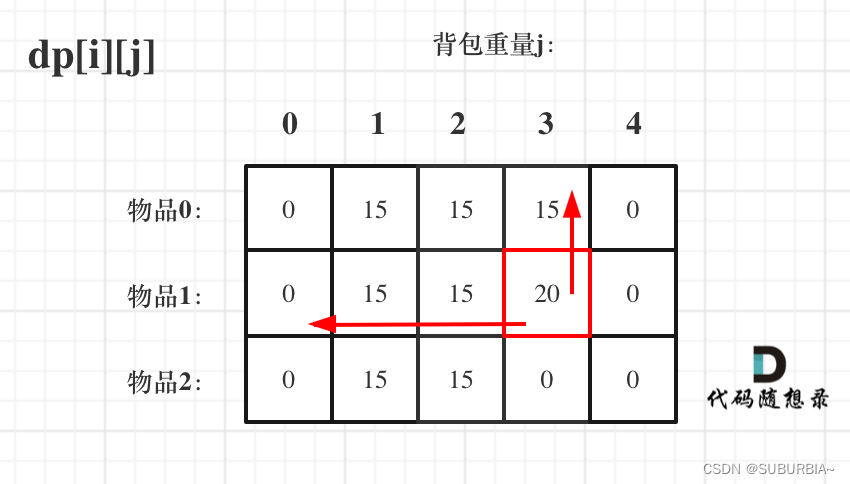
public class BagProblem {public static void main(String[] args) {int[] weight = {1,3,4};int[] value = {15,20,30};int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){// 创建dp数组int goods = weight.length; // 获取物品的数量int[][] dp = new int[goods][bagSize + 1];// 初始化dp数组// 创建数组后,其中默认的值就是0for (int j = weight[0]; j <= bagSize; j++) {dp[0][j] = value[0];}// 填充dp数组for (int i = 1; i < weight.length; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]) {/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/dp[i][j] = dp[i-1][j];} else {/*** 当前背包的容量可以放下物品i* 那么此时分两种情况:* 1、不放物品i* 2、放物品i* 比较这两种情况下,哪种背包中物品的最大价值最大*/dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);}}}// 打印dp数组for (int i = 0; i < goods; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}}
}一维 dp 数组(滚动数组)
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组初始化的时候,都初始为0就可以了。
注意: 遍历背包的顺序是倒序遍历,保证物品只放入一次。
从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWight = 4;testWeightBagProblem(weight, value, bagWight);
}public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++){for (int j = bagWeight; j >= weight[i]; j--){dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}//打印dp数组for (int j = 0; j <= bagWeight; j++){System.out.print(dp[j] + " ");}分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
本题要求集合里能否出现总和为 sum / 2 的子集。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
dp[0]一定是0。如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
class Solution {public boolean canPartition(int[] nums) {if(nums == null || nums.length == 0) return false;int n = nums.length;int sum = 0;for (int num : nums) {sum += num;}if (sum % 2 != 0) return false;int target = sum / 2;int[] dp = new int[target + 1];for (int i = 0; i < n; i++) {for (int j = target; j >= nums[i]; j--) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}if(dp[target] == target) return true;} return dp[target] == target;}
}
相关文章:

代码随想录算法训练营第四一天 | 背包问题
目录 背包问题01背包二维dp数组01背包一维 dp 数组(滚动数组)分割等和子集 LeetCode 背包问题 01背包 有n件物品和一个最多能背重量为 w 的背包,第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次&#x…...
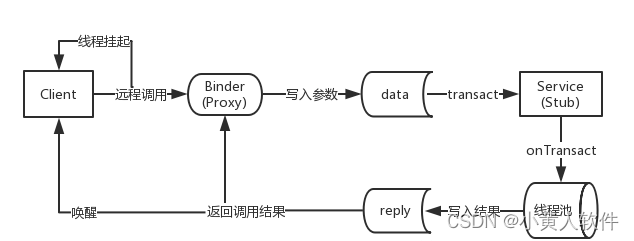
AIDL的工作原理与使用示例 跨进程通信 远程方法调用RPC
AIDL的介绍与使用 AIDL(Android Interface Definition Language)是Android中用于定义客户端和服务端之间通信接口的一种接口定义语言。它允许你定义客户端和服务的通信协议,用于在不同的进程间或同一进程的不同组件间进行数据传递。AIDL通过…...

K8S部署Java项目 pod报错 logs日志内容:no main manifest attribute, in app.jar
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

SQL实现模糊查询的四种方法总结
目录 一、一般模糊查询 二、利用通配符查询 1. _ 表示任意的单个字符 2. % 表示匹配任意多个任意字符 3. [ ]表示筛选范围 4. 查询包含通配符的字符串 一、一般模糊查询 1. 单条件查询 //查询所有姓名包含“张”的记录select * from student where name like 张 2. 多条…...
)
爬虫基本库的使用(urllib库的详细解析)
学习爬虫,其基本的操作便是模拟浏览器向服务器发出请求,那么我们需要从哪个地方做起呢?请求需要我们自己构造吗? 我们需要关心请求这个数据结构怎么实现吗? 需要了解 HTTP、TCP、IP层的网络传输通信吗? 需要知道服务器如何响应以及响应的原理吗? 可…...
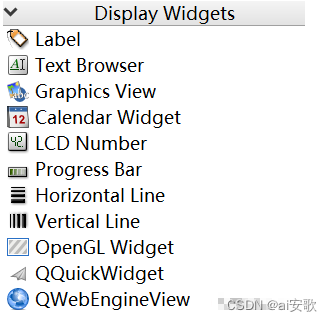
【PyQt5桌面应用开发】3.Qt Designer快速入门(控件详解)
一、Qt Designer简介 Qt Designer是PyQt程序UI界面的实现工具,可以帮助我们快速开发 PyQt 程序的速度。它生成的 UI 界面是一个后缀为 .ui 的文件,可以通过 pyiuc 转换为 .py 文件。 Qt Designer工具使用简单,可以通过拖拽和点击完成复杂界面…...
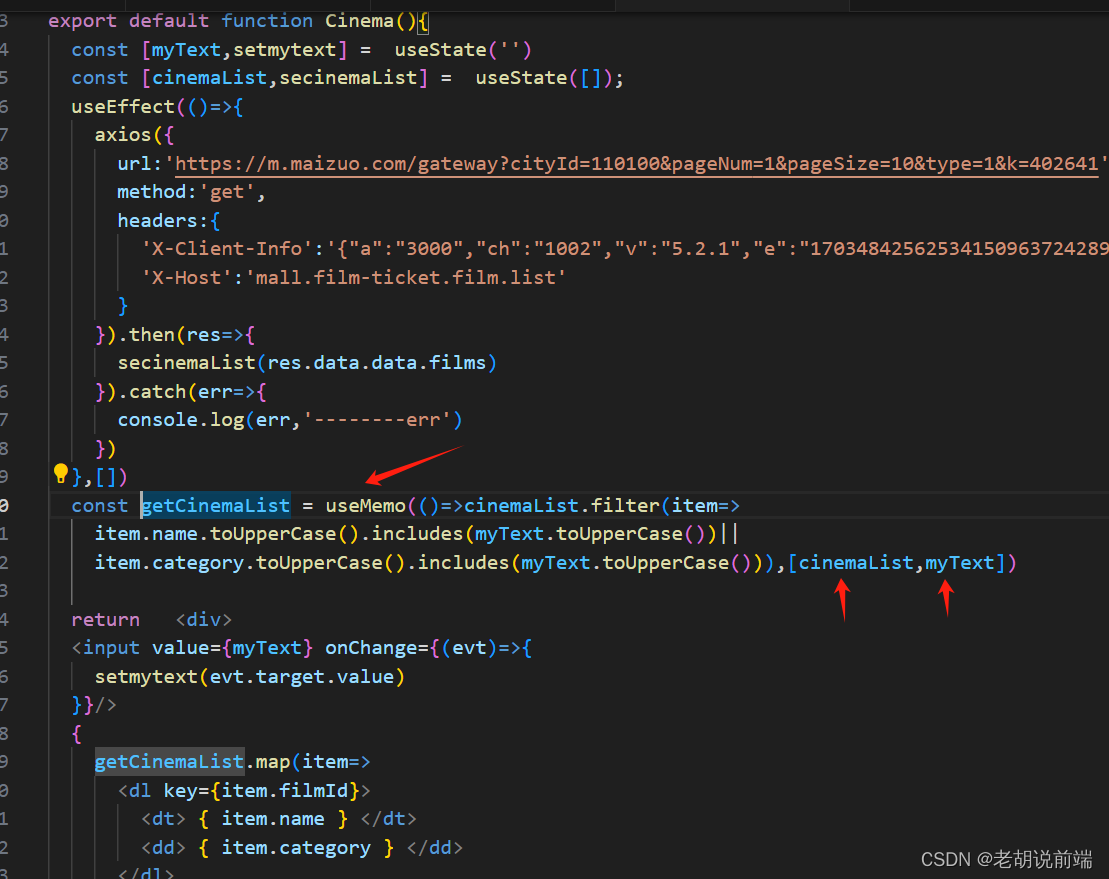
react useMemo 用法
1,useCallback 的功能完全可以由 useMemo 所取代,如果你想通过使用 useMemo 返回一个记忆函数也是完全可以的。 usecallback(fn,inputs)is equivalent to useMemo(()> fn, inputs). 区别是:useCallback不会执行第一个参数函数,而是将它返…...

python学习笔记 - 标准库函数
概述 为了方便程序员快速编写Python脚本程序,Python提供了很多好用的功能模块,它们内置于Python系统,也称为内置函数(Built-in Functions,BlF),Python 内置函数是 Python 解释器提供的一组函数,无需额外导…...
校招失败后,在小公司熬了 2 年终于进了字节跳动,竭尽全力....
其实两年前校招的时候就往字节投了一次简历,结果很明显凉了,随后这个理想就被暂时放下了,但是这个种子一直埋在心里这两年除了工作以外,也会坚持写博客,也因此结识了很多优秀的小伙伴,从他们身上学到了特别…...

PYTHON-使用正则表达式进行模式匹配
目录 Python 正则表达式Finding Patterns of Text Without Regular ExpressionsFinding Patterns of Text with Regular ExpressionsCreating Regex ObjectsMatching Regex ObjectsReview of Regular Expression MatchingMore Pattern Matching with Regular ExpressionsGroupi…...

Fiddler工具 — 19.Fiddler抓包HTTPS请求(二)
5、查看证书是否安装成功 方式一: 点击Tools菜单 —> Options... —> HTTPS —> Actions 选择第三项:Open Windows Certificate Manager打开Windows证书管理器。 打开Windows证书管理器,选择操作—>查看证书,在搜索…...

架构设计:流式处理与实时计算
引言 随着大数据技术的不断发展,流式处理和实时计算在各行各业中变得越来越重要。那么什么是流式处理呢?我们又该怎么使用它?流式处理允许我们对数据流进行实时分析和处理,而实时计算则使我们能够以低延迟和高吞吐量处理数据。本…...

Linux系统安装zookeeper
Linux安装zookeeper 安装zookeeper之前需要安装jdk,确认jdk环境没问题之后再开始安装zookeeper 下载zookeeper压缩包,官方下载地址:Apache Download Mirrors 将zookeeper压缩包拷贝到Linux并解压 # (-C 路径)可以解压到指定路径 tar -zxv…...

【前端素材】推荐优质后台管理系统Modernize平台模板(附源码)
一、需求分析 后台管理系统是一种用于管理和控制网站、应用程序或系统后台操作的软件工具,通常由授权用户(如管理员、编辑人员等)使用。它提供了一种用户友好的方式来管理网站或应用程序的内容、用户、数据等方面的操作,并且通常…...
二、Vue组件化编程
2、Vue组件化编程 2.1 非单文件组件 <div id"root"><school></school><hr><student></student> </div> <script type"text/javascript">//创建 school 组件const school Vue.extend({template: <div&…...
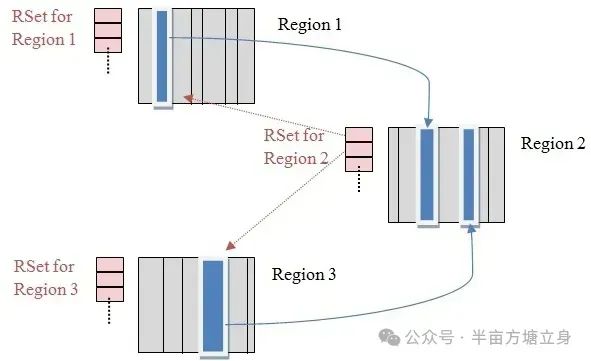
JVM跨代引用垃圾回收
1. 跨代引用概述 在Java堆内存中,年轻代和老年代之间存在的对象相互引用,假设现在要进行一次新生代的YGC,但新生代中的对象可能被老年代所引用的,为了找到新生代中的存活对象,不得不遍历整个老年代。这样明显效率很低…...
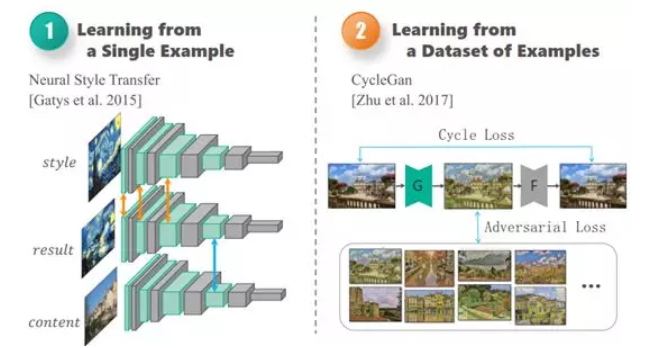
AI:135-基于卷积神经网络的艺术品瑕疵检测与修复
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带关键代码,详细讲解供大家学习,希望…...

C++标准头文件汇总及功能说明
文章目录 algorithmbitsetcctypecerrnoclocalecmathcstdioctimedequeiostreamexceptionfstreamfunctionallimitslistmapiosiosfwdsetsstreamstackstdexceptstreambufcstringutilityvectorcwcharcwctype algorithm algorithm头文件是C的标准算法库,它主要用在容器上。…...
)
glTF 添加数据属性(extras)
使用3D 模型作为可视化界面的一个关键是要能够在3D模型中添加额外的数据属性,利用这些数据属性能够与后台的信息模型建立对应关系,例如后台信息模型是opcua 信息模型的话,在3D模型中要能够包含OPC UA 的NodeId,BrowserName 等基本…...
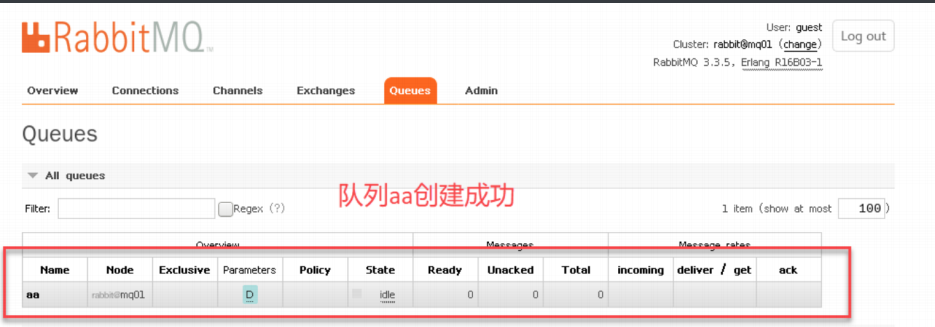
linux系统消息中间件rabbitmq普通集群的部署
rabbitmq普通集群的部署 普通集群准备环境查询版本对应安装rabbitmq软件启动创建登录用户开启用户远程登录查看端口 部署集群创建数据存放目录和日志存放目录:拷⻉erlang.cookie将其他两台服务器作为节点加⼊节点集群中查看集群状态创建新的队列 普通集群准备环境 配置hosts⽂件…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
深入理解 C++ 左值右值、std::move 与函数重载中的参数传递
在 C 编程中,左值和右值的概念以及std::move的使用,常常让开发者感到困惑。特别是在函数重载场景下,如何合理利用这些特性来优化代码性能、确保语义正确,更是一个值得深入探讨的话题。 在开始之前,先提出几个问题&…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...
