算法简介:查找与算法运行时间
文章目录
- 1. 二分查找与简单查找
- 1.1 运行时间
- 2. 旅行商问题
算法是一组完成任务的指令。任何代码片段都可以视为算法。
1. 二分查找与简单查找
二分查找是一种算法,其输入是一个有序的元素列表,如果要查找的元素包含在列表中,二分查找返回其位置;否则返回NULL。二分查找每次都检查中间的元素。
def binary_search(list, item):
low = 0
high = len(list) - 1
while low <= highmid = (low + high)/2guess = list[mid]if guess == item:return midif guess > item:high = mid - 1else:low = mid + 1
return None
简单查找即将元素全部遍历。
1.1 运行时间
大O表示法:一种特殊的表示法,指出算法的速度有多块。
大O表示法指的并非以秒为单位的速度。大O表示法让你能够比较操作数,它指出了算法运行时间的增速。
假设有10亿个元素有序排列,需要查找其中的一个元素,没查找一个元素需要消耗1毫秒,则简单查找需要11天左右,二分查找需要30ms。
假设列表有n个元素。
- 简单查找需要查找每个元素,因此需要执行n次操作,使用大O表示法,这个运行时间为O(n)。
- 二分查找需要执行log n次操作,使用大O表示为O(log n)。
大O表示法指出了最糟情况下的运行时间。
一些常见的大O运行时间:
O(log n),对数时间,如二分查找
O(n),线性时间,如简单查找
O(n*log n),如快速排序
O(n^2),如选择排序
O(n!),如旅行商问题
- 算法的速度指的并非时间,而是操作数的增速。、
- 谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加。
- 算法的运行时间用大O表示法表示。
- O(log n)比O(n)快,当需要搜索的元素越多时,前者比后者快的越多。
2. 旅行商问题
有一位旅行商。他需要前往5个城市,同时需要确保旅途最短。为此,可考虑前往各个城市的各种可能顺序。
对于每种顺序,他都计算总旅程,再挑选出旅程最短的路径。
- 5个城市有120钟不同的排列方式。
- 涉及6个城市时,需要执行720次操作。
- 涉及7个城市时,需要执行5040次操作。
- 涉及n个城市时,需要执行n!(n的阶乘)次操作。因此运行时间为O(n!),即阶乘时间。
相关文章:

算法简介:查找与算法运行时间
文章目录 1. 二分查找与简单查找1.1 运行时间 2. 旅行商问题 算法是一组完成任务的指令。任何代码片段都可以视为算法。 1. 二分查找与简单查找 二分查找是一种算法,其输入是一个有序的元素列表,如果要查找的元素包含在列表中,二分查找返回…...

零基础C++开发上位机--基于QT5.15的串口助手(三)
本系列教程本着实践的目的,争取每一节课都带大家做一个小项目,让大家多实践多试验,这样才能知道自己学会与否。 接下来我们这节课,主要学习一下QT的串口编程。做一款自己的串口助手,那么这里默认大家都是具备串口通信…...

Facebook的虚拟社交愿景:元宇宙时代的新起点
在当今数字化时代,社交媒体已经成为人们生活中不可或缺的一部分。而随着科技的不断进步和社会的发展,元宇宙已经成为了人们关注的热点话题之一。作为社交媒体的领军企业之一,Facebook也在积极探索虚拟社交的未来,将其视为元宇宙时…...

【深度学习笔记】4_6 模型的GPU计算
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图 4.6 GPU计算 到目前为止,我们一直在使用CPU计算。对复杂的神经网络和大规模的数据来说,使用CPU来计算可能不够…...

留学申请过程中如何合理使用AI?大学招生官怎么看?
我们采访过的学生表示,他们在写essay的过程中会使用 ChatGPT,主要用于以下两个方面:第一,生成想法和头脑风暴;第二,拼写和语法检查。 纽约时报的娜塔莎辛格(Natasha Singer)在一篇文…...

vue2与vue3的diff算法有什么区别
在 Vue 中,虚拟 DOM 是一种重要的概念,它通过将真实的 DOM 操作转化为对虚拟 DOM 的操作,从而提高应用的性能。Vue 框架在虚拟 DOM 的更新过程中采用了 Diff 算法,用于比较新旧虚拟节点树,找出需要更新的部分ÿ…...
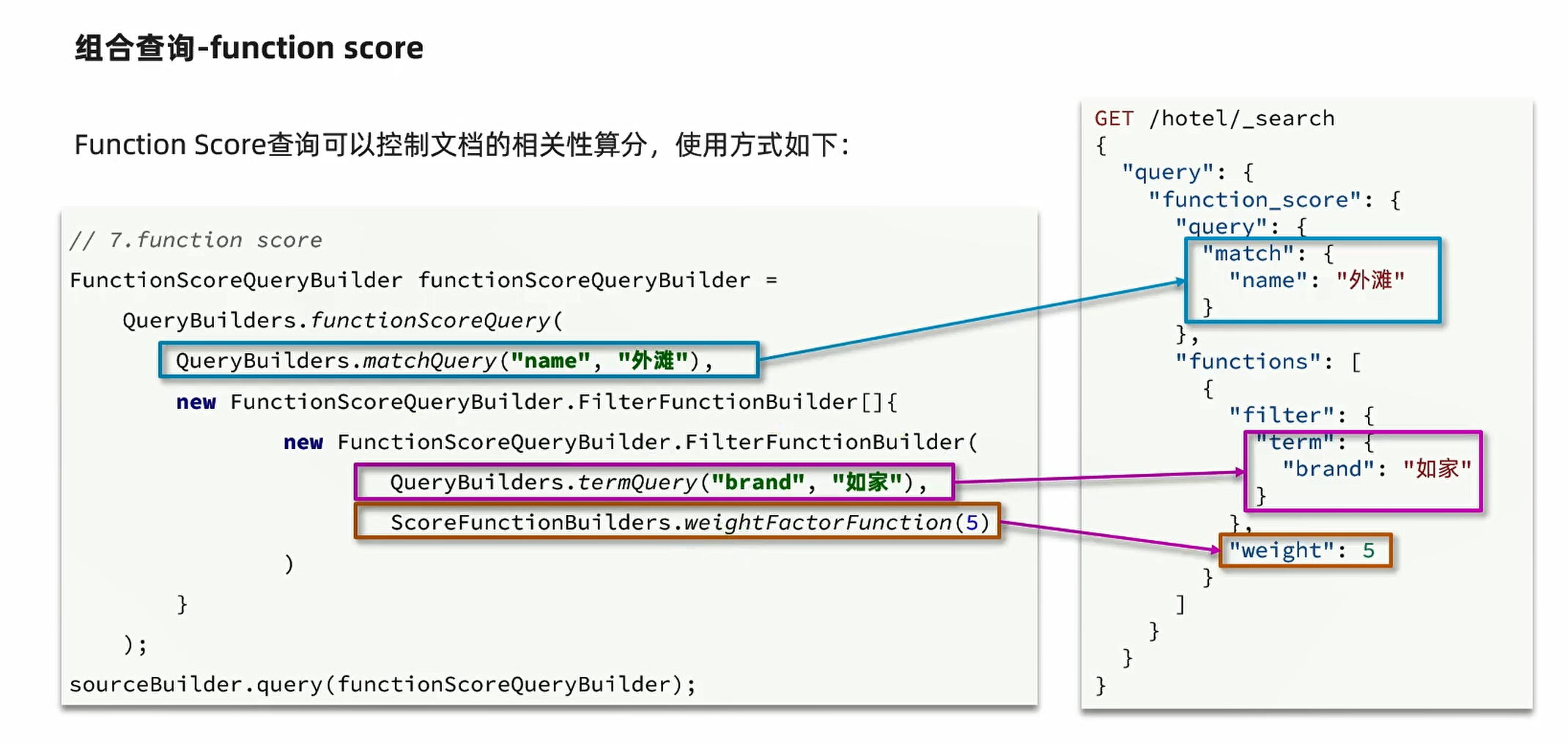
ES小总结
组合查询 FunctionScoreQueryBuilder functionScoreQuery QueryBuilders.functionScoreQuery(boolQuery,new FunctionScoreQueryBuilder.FilterFunctionBuilder[]{new FunctionScoreQueryBuilder.FilterFunctionBuilder(QueryBuilders.termQuery("isAD",true),Score…...

vue2与vue3中父子组件传参的区别
本次主要针对vue中父子组件传参所进行讲解 一、vue2和vue3父传子区别 1.vue2的父传子 1).在父组件子标签中自定义一个属性 <sonPage :子组件接收到的类名"传输的数据">子组件</sonPage> 2).在子组件中peops属性中拿到自定属性 props: {子组件接收的…...

使用vuetify实现全局v-alert消息通知
前排提示,本文为引流文,文章内容不全,更多信息前往:oldmoon.top 查看 简介 使用强大的Vuetify开发前端页面,结果发现官方没有提供简便的全局消息通知组件(像Element中的ElMessage那样)…...

CentOS 7.9上编译wireshark 3.6
工作环境是Centos 7.9,原本是通过flathub安装的wireshark,但是在gnome的application installer上升级到wireshark 4.2.3之后就运行不起来了,flatpak run org.wireshark.Wireshark启动提示缺少qt6,查了一下wireshark新版是依赖qt6的…...

初学学习408之数据结构--数据结构基本概念
初学学习408之数据结构我们先来了解一下数据结构的基本概念。 数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。 本内容来源于参考书籍《大话数据结构》与《王道数据结构》。除去书籍中的内容,作为初学者的我会尽力详细直白地介绍数据结构的…...

Java项目中必须使用本地缓存的几种情况
Java项目中必须使用本地缓存的几种情况 在Java项目的开发过程中,为了提高应用的性能和响应速度,缓存机制经常被使用。其中,本地缓存作为一种常见的缓存方式,将数据存储在应用程序的本地内存或磁盘中,以便快速访问。下…...
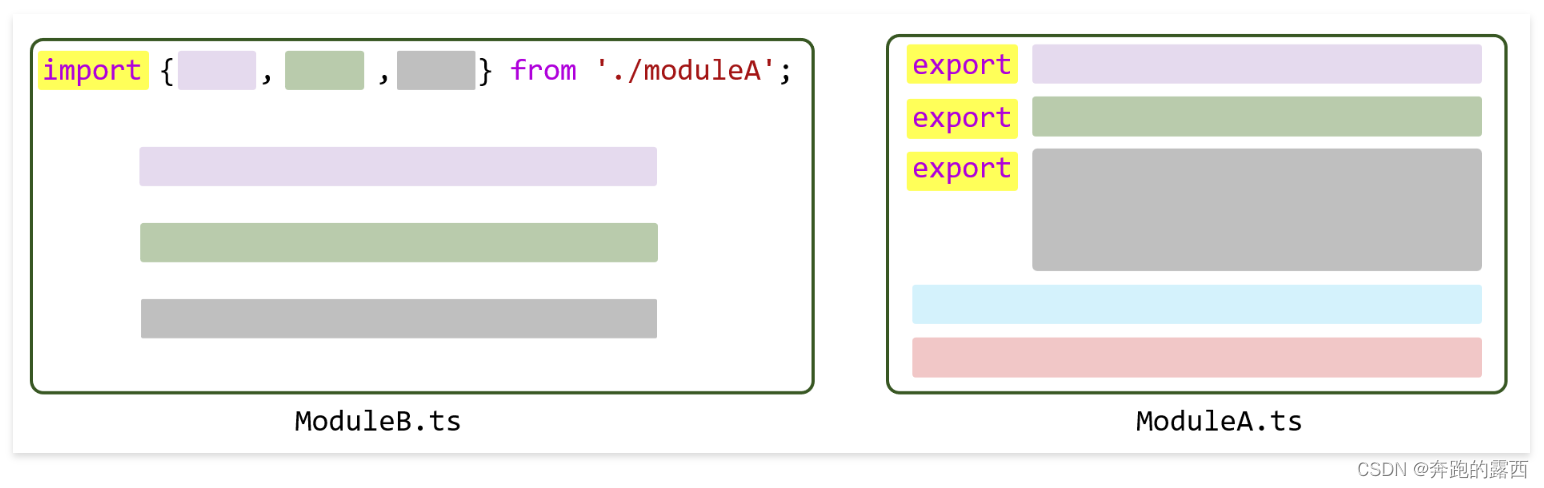
【鸿蒙 HarmonyOS 4.0】TypeScript开发语言
一、背景 HarmonyOS 应用的主要开发语言是 ArkTS,它由 TypeScript(简称TS)扩展而来,在继承TypeScript语法的基础上进行了一系列优化,使开发者能够以更简洁、更自然的方式开发应用。值得注意的是,TypeScrip…...
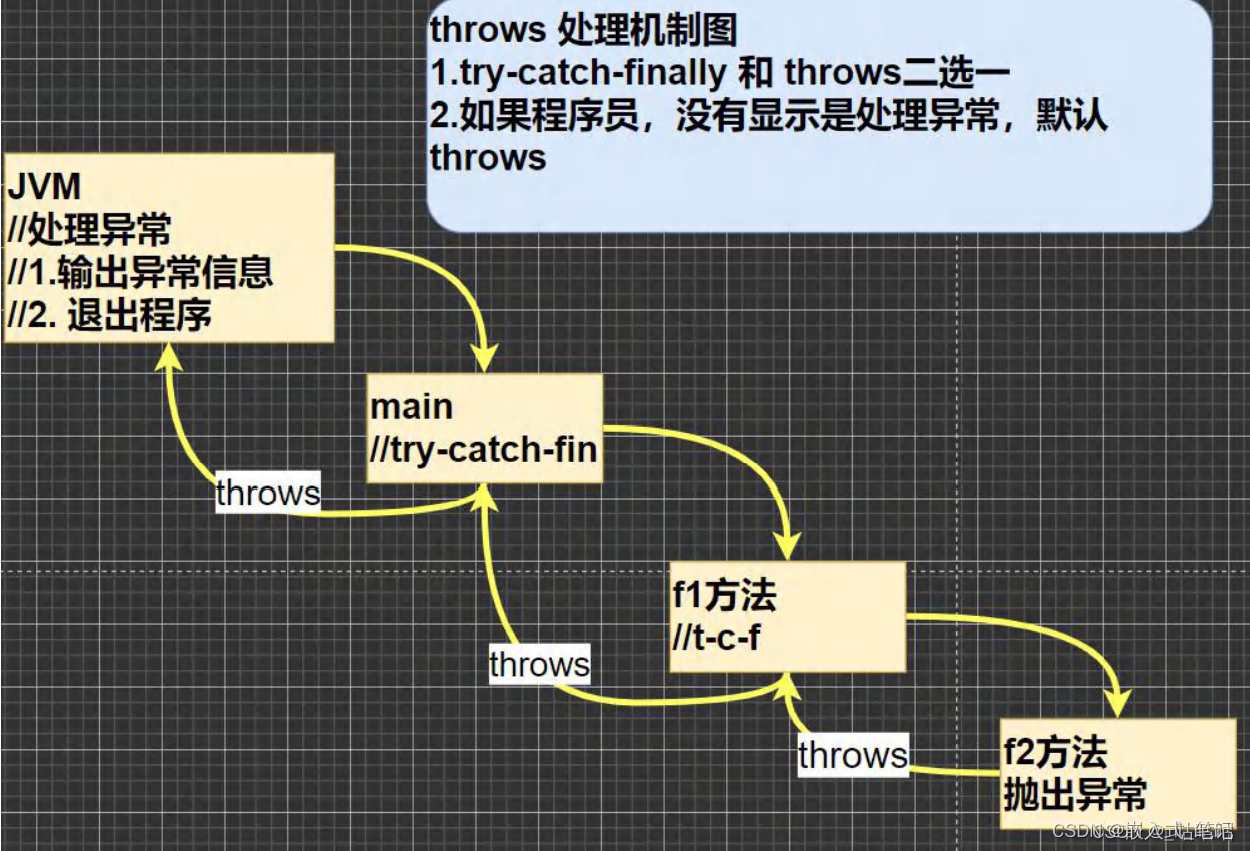
Android java基础_异常
一.异常的概念 在Java中,异常(Exception)是指程序执行过程中可能出现的不正常情况或错误。它是一个事件,它会干扰程序的正常执行流程,并可能导致程序出现错误或崩溃。 异常在Java中是以对象的形式表示的,…...
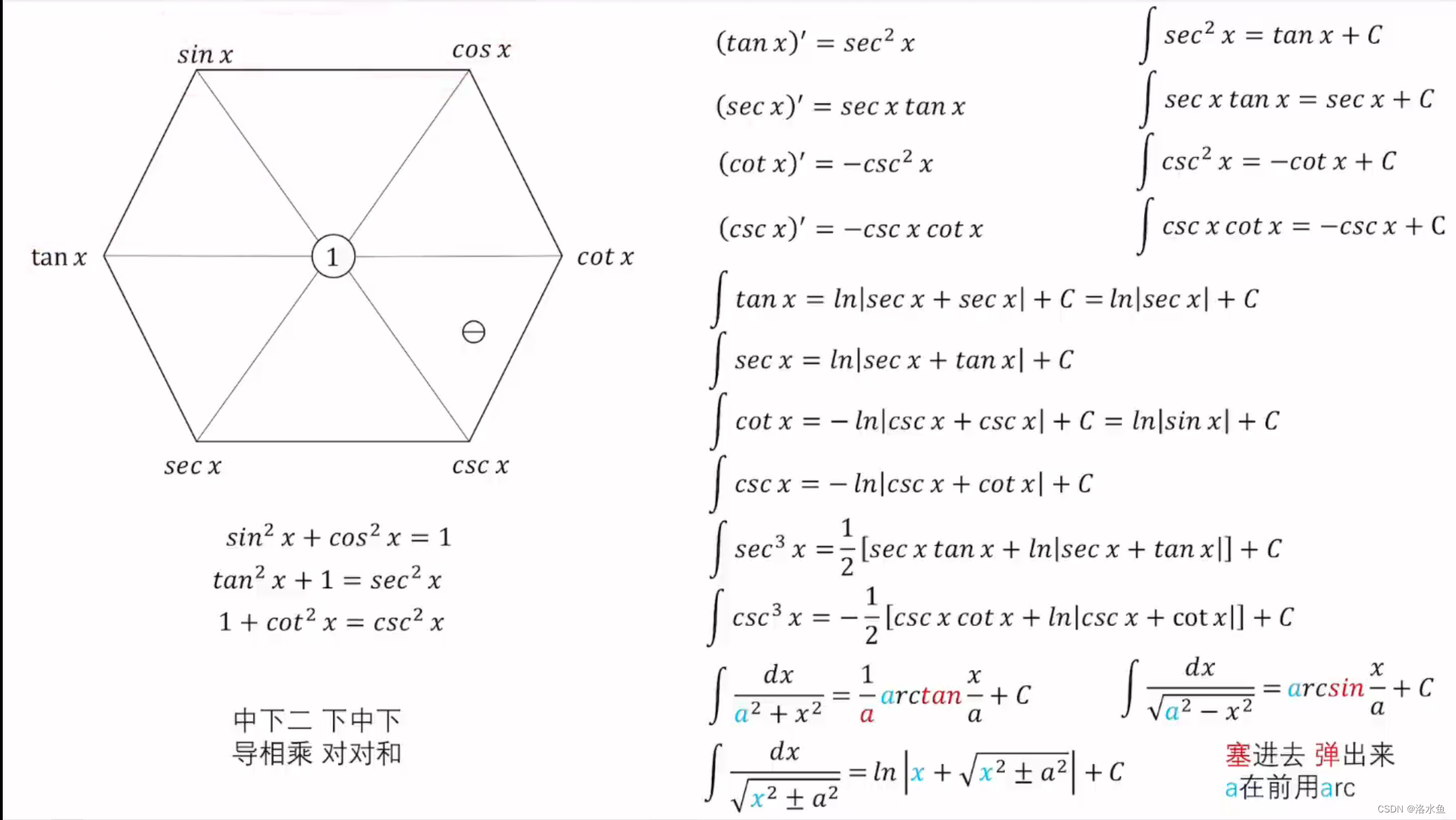
高数考研 -- 公式总结(更新中)
1. 两个重要极限 (1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …...

详解顺序结构滑动窗口处理算法
🎀个人主页: https://zhangxiaoshu.blog.csdn.net 📢欢迎大家:关注🔍点赞👍评论📝收藏⭐️,如有错误敬请指正! 💕未来很长,值得我们全力奔赴更美好的生活&…...

Java 8中使用Stream来操作集合
Java 8中使用Stream来操作集合 在Java 8中,你可以使用Stream API来操作集合,这使得集合的处理变得更加简洁和函数式。Stream API提供了一系列的中间操作(intermediate operations)和终端操作(terminal operations&…...

MATLAB环境下一种改进的瞬时频率(IF)估计方法
相对于频率成分单一、周期性强的平稳信号来说,具有非平稳、非周期、非可积特性的非平稳信号更普遍地存在于自然界中。调频信号作为非平稳信号的一种,由于其频率时变、距离分辨率高、截获率低等特性,被广泛应用于雷达、地震勘测等领域。调频信…...

解决:selenium web browser 的版本适配问题
文章目录 解决方案:使用 webdriver manager 自动适配驱动 使用 selenium 操控浏览器的时候报错: The chromedriver version (114.0.5735.90) detected in PATH at /opt/homebrew/bin/chromedriver might not be compatible with the detected chrome ve…...

pytest.param作为pytest.mark.parametrize的参数进行调用
pytest.param:在 pytest.mark.parametrize 中可以作为一个指定的参数进行调用 获取数据库(网页端)数据,通过pytest.param包装成数据包用于pytest.mark.parametrize 中实现数据驱动调用。 import os import pytest import json fr…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
