用CSS制作弧形卡片的三种创意方法!
在平时开发中,有时候会碰到下面这种“弧形”样式,主要分为“内凹”和“外凸”两种类型,如下

该如何实现呢?或者想一下,有哪些 CSS 属性和“弧形”有关?下面介绍 3 种方式,一起看看吧
一、border-radius
通常情况下,我们用border-radius都是这样
div{border-radius: 20px;
}
这样表示 4 个角都是圆角,并且是标准的正圆

其实,border-radius还支持斜杠的写法,比如
div{border-radius: 20px / 10px;
}
这表示,圆角是一个x半径为20px,y半径为10px的椭圆,如下

放大来看,其实是这样的
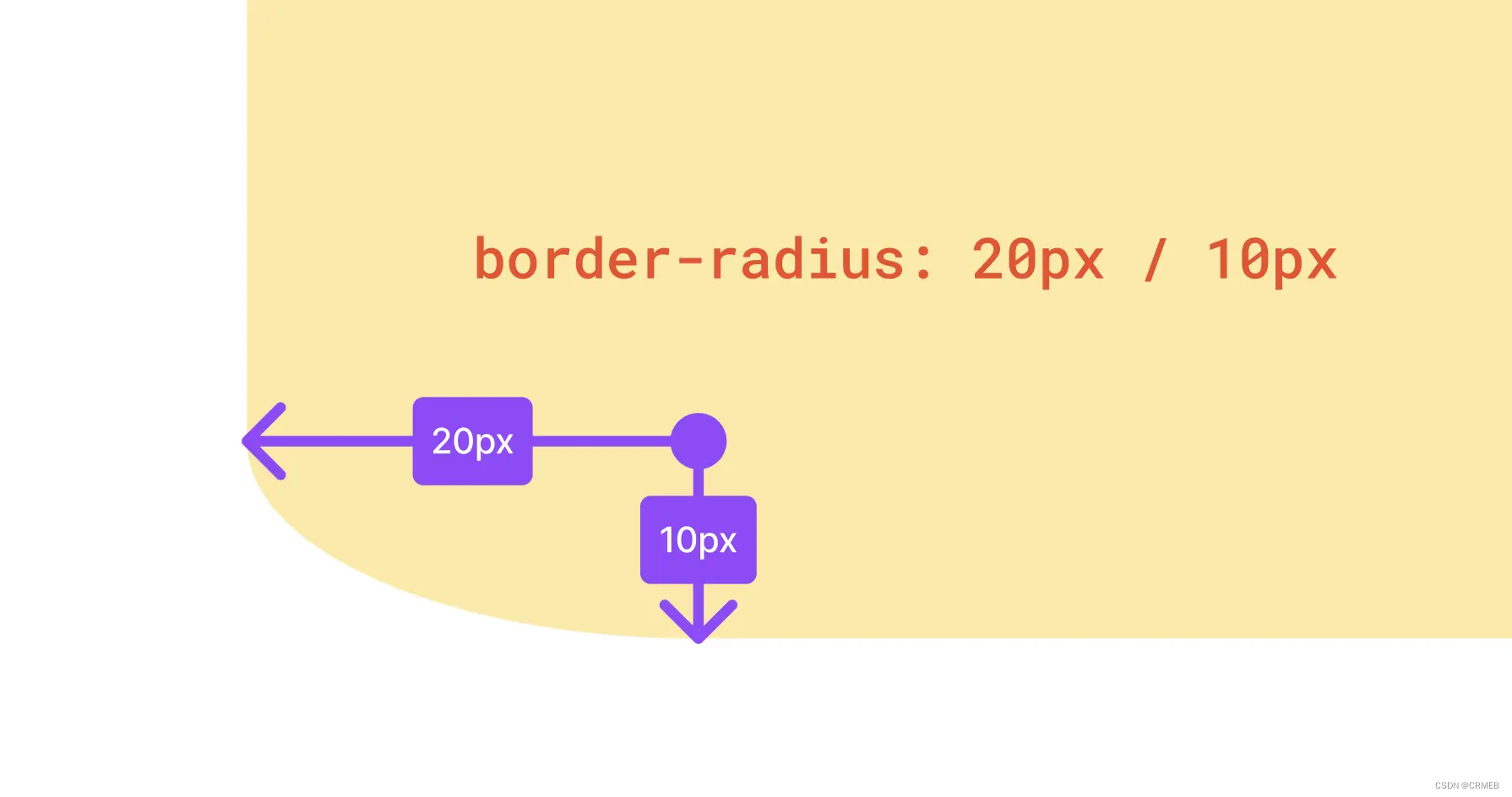
进一步,我们将x半径设置成50%,这样就能得到一个完整的弧形了
div{border-radius: 50% / 20px;
}
效果如下

这样就得到了“外凸”的弧形了,是不是很容易?
至于“内凹”弧形,单纯的border-radius表示无能为力,可以看接下来的方式
二、伪元素+border-radius
这个其实大多数同学都能想到的方式,一个矩形和一个椭圆组合起来,不就是一个弧形卡片了吗?原理非常简单
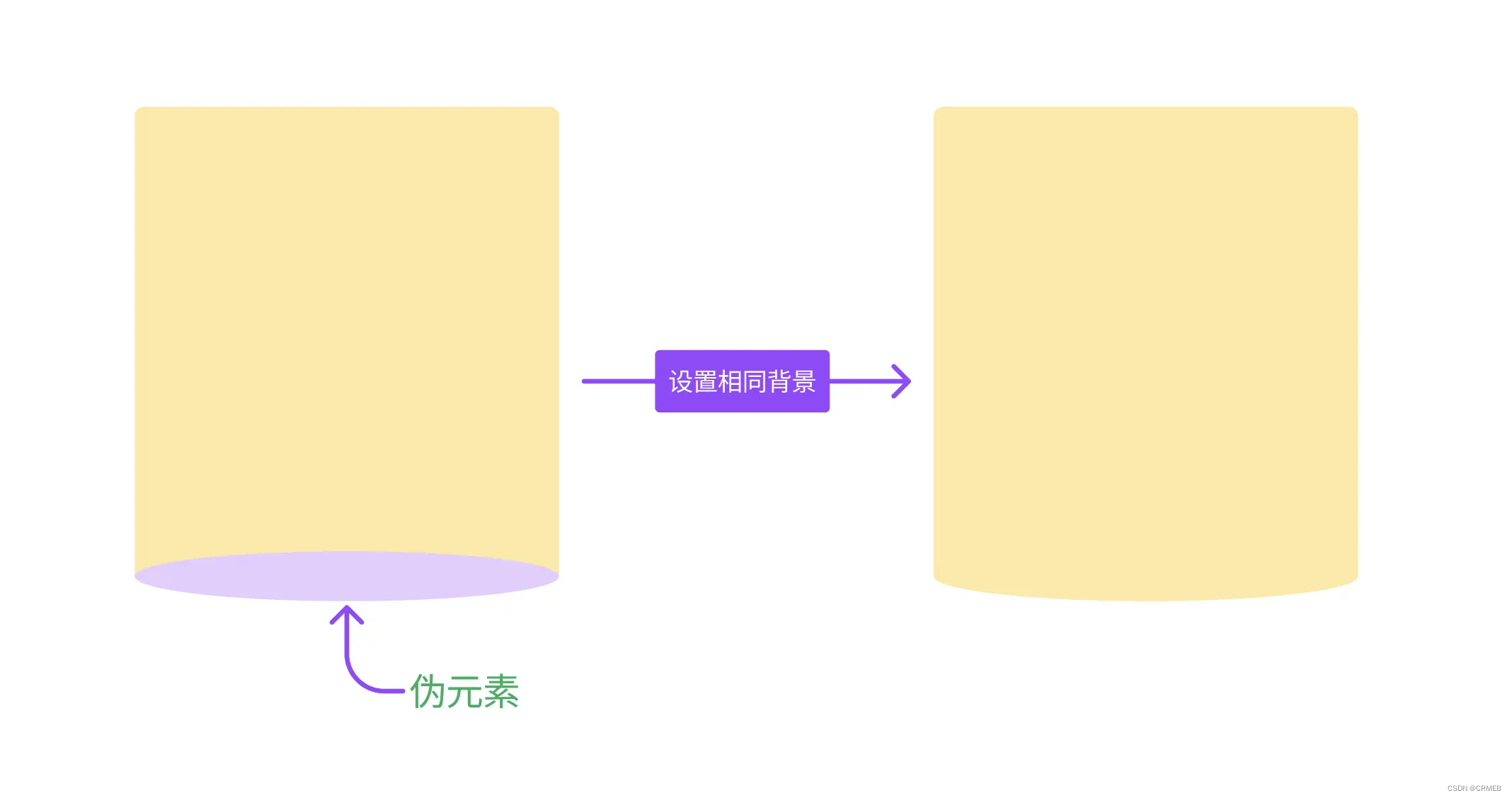
用代码实现就是
div{position: relative;
}
div::after{content: '';position: absolute;width: 100%;height: 20px;border-radius: 100%;background: inherit; /* 继承父级背景 */bottom: 0;left: 50%;transform: translate(-50%,50%);
}
效果如下(虚线表示伪元素的边缘)

用伪元素的好处是,可以随意控制弧度的大小和位置,这个是border-radius所不能比的
通过overflow:hidden裁剪多余部分,可以得到一个边缘比较“锋利”的弧形,如下所示
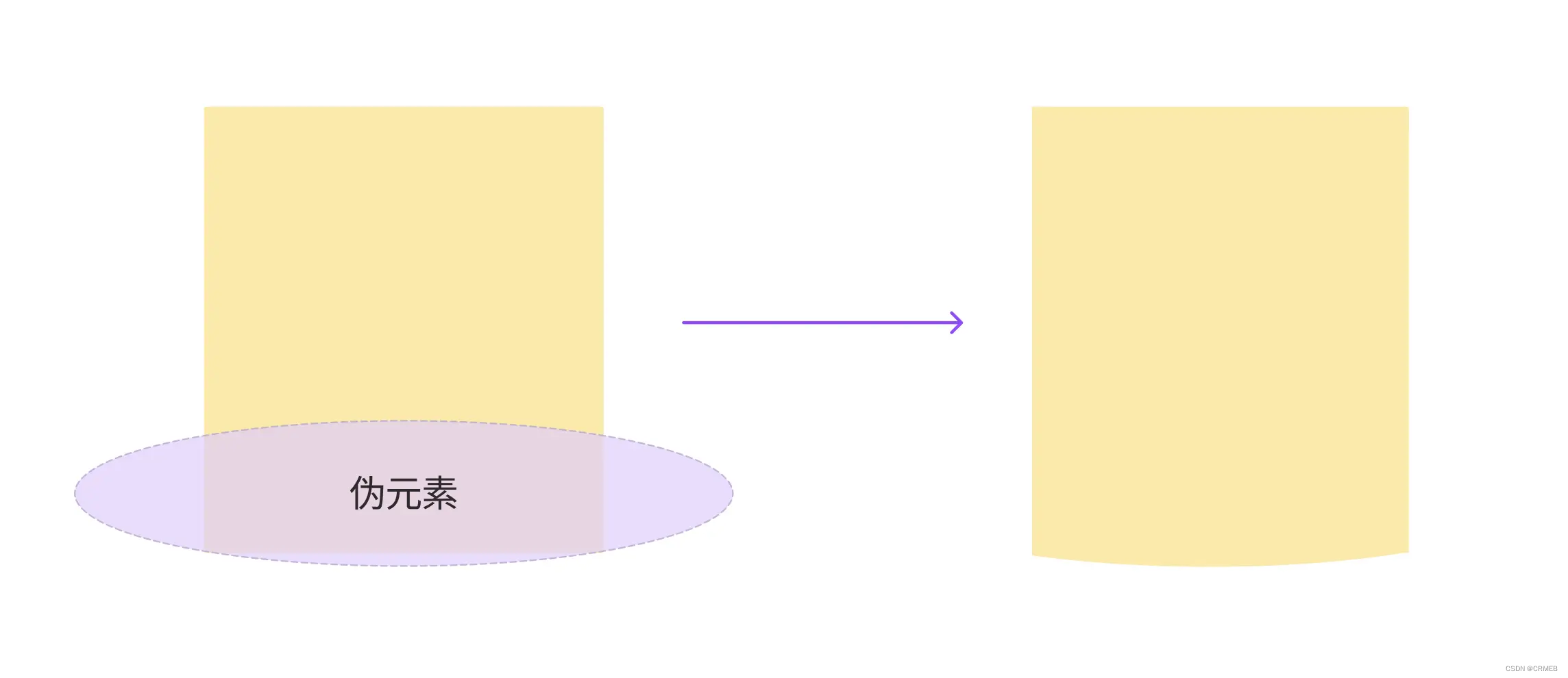
另外,用伪元素还能实现“内凹”的效果,不过这需要反过来思考,什么意思呢?之前是给伪元素加的背景,现在需要加在伪元素的外围,这里用box-shadow实现,原理如下
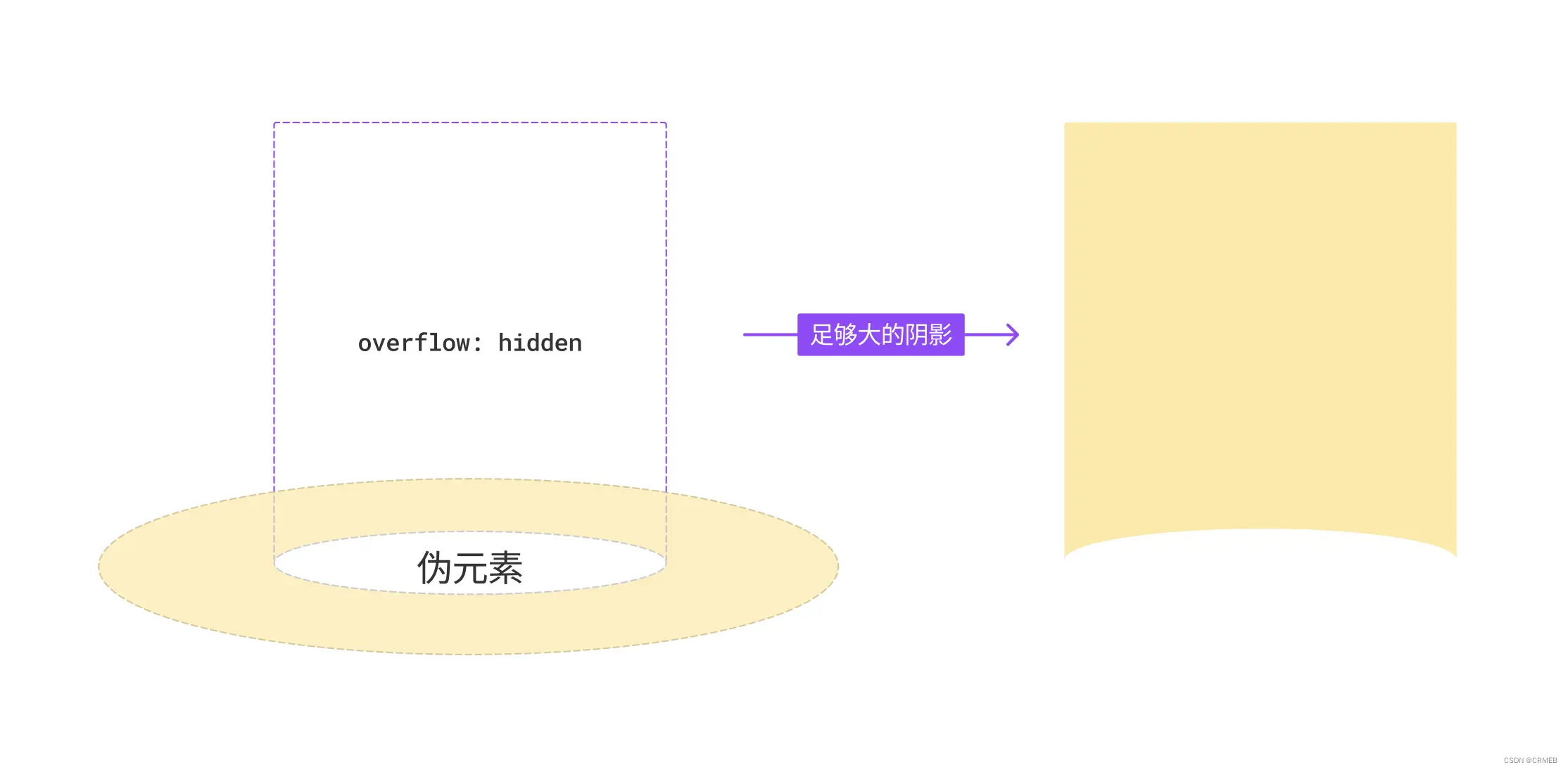
用代码实现就是
div{background: none;overflow: hidden;
}
div::after{content: '';background: none;box-shadow: 0 0 0 9999vh #FFE8A3; /*足够大的阴影*/z-index: -1;
}
效果如下(虚线表示伪元素的边缘)

三、径向渐变
提到圆弧,还可以想到径向渐变,没错,这里通过径向渐变也能轻易实现弧形卡片效果。
先来看“外凸”的,其实思路和伪元素一样,先拆分,一个椭圆和一个矩形,对应的就是径向渐变(radial-gradient)和线性渐变(linear-gradient),如下
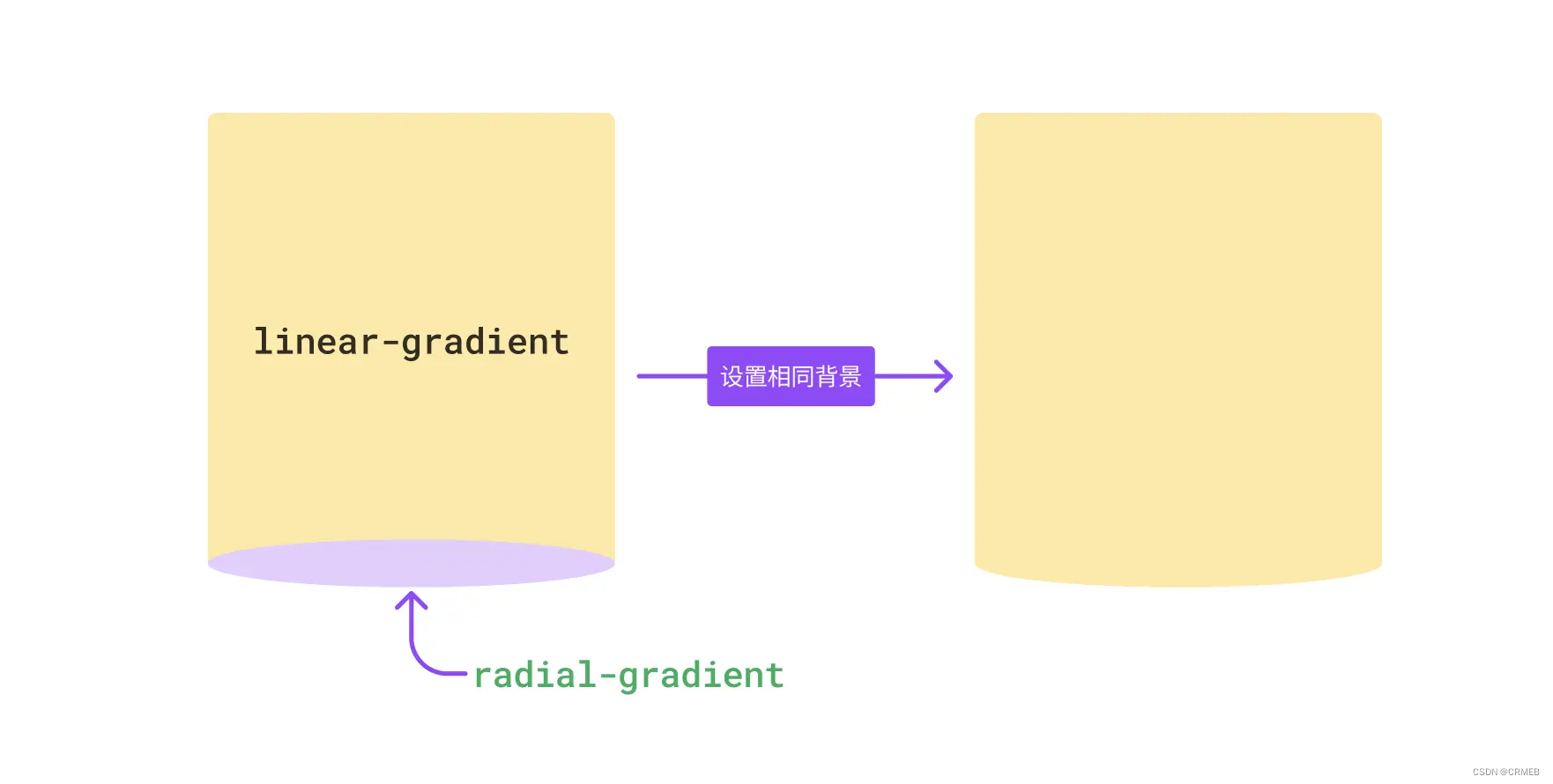
用代码实现就是
div{background: radial-gradient(closest-side, #9747FF 100%,transparent 0) center bottom/100% 20px no-repeat,linear-gradient(#FFE8A3, #FFE8A3) 0 0/100% calc(100% - 10px) no-repeat;
}
效果如下(紫色部分是径向渐变)
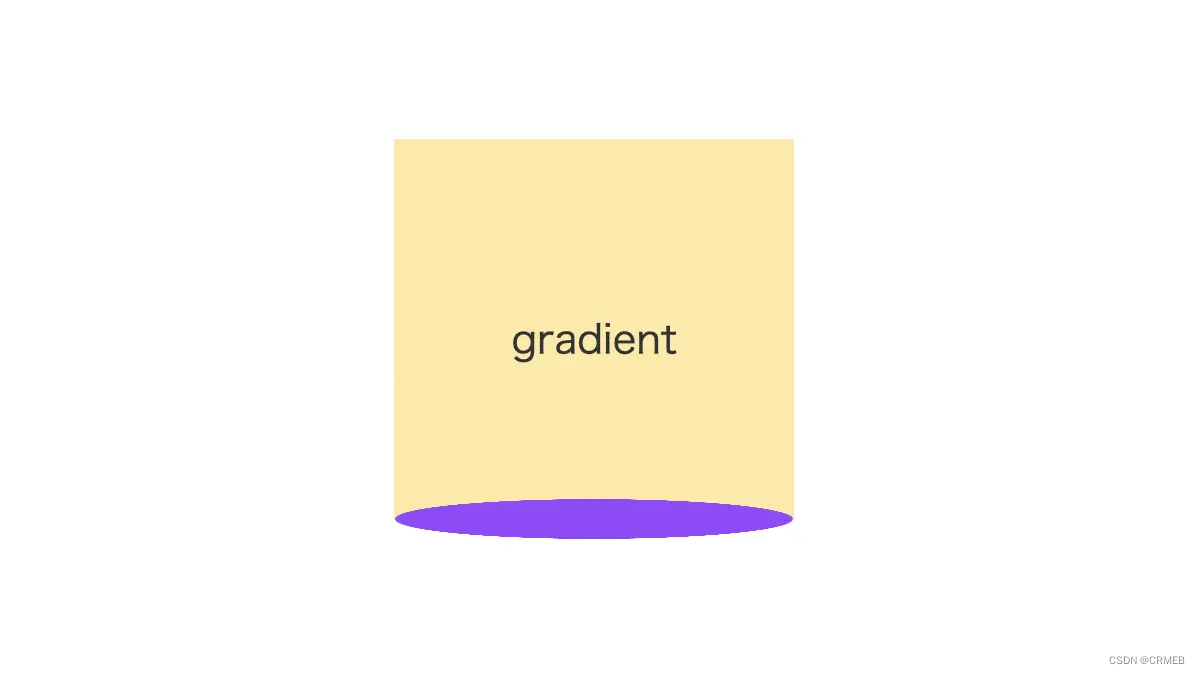
再来看“内凹”的弧形,其实也和伪元素思路类似,只不过这里需要绘制一个足够大的渐变,从透明到纯色的径向渐变,示意如下
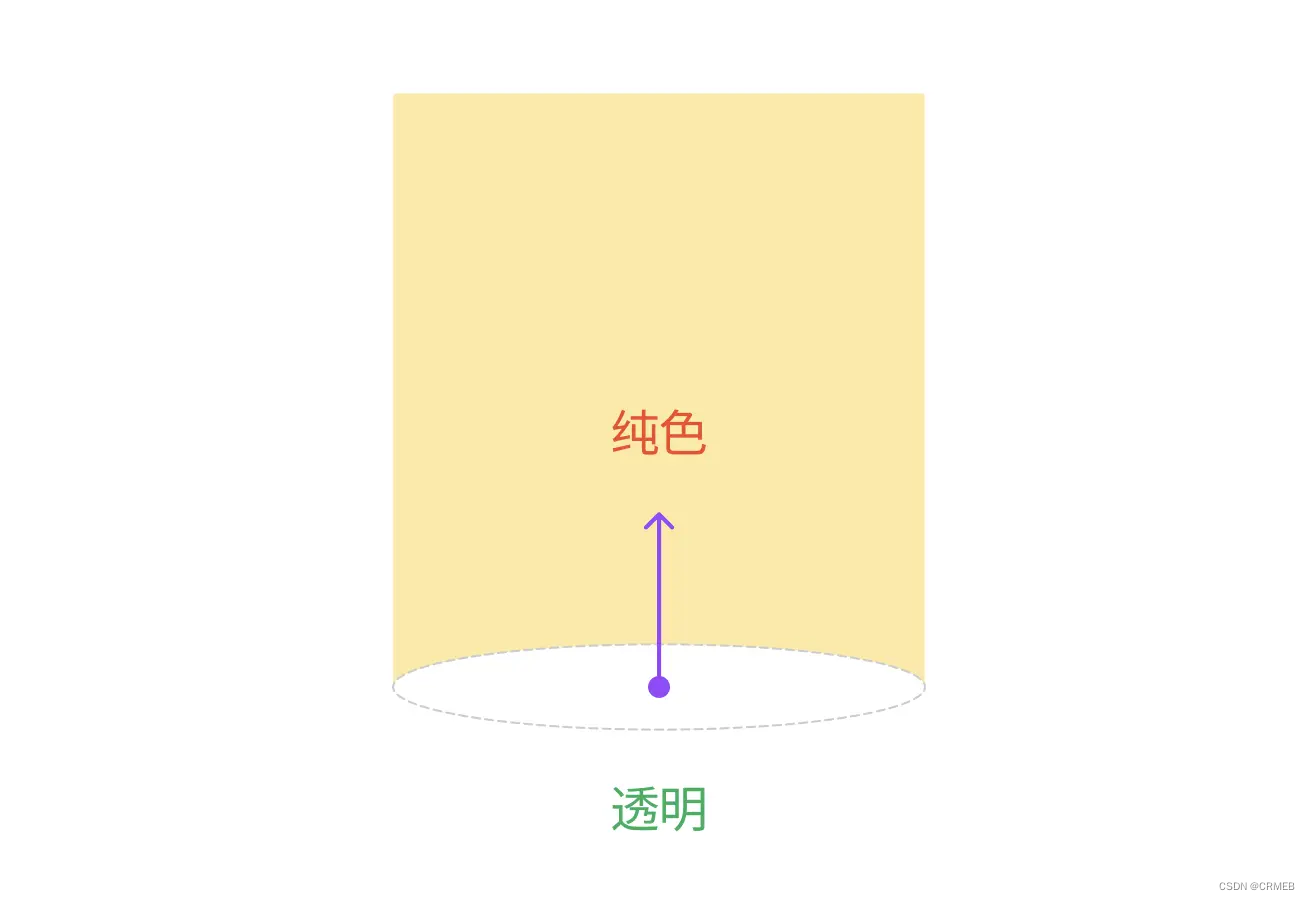
调整好渐变中心点,用代码实现就是
div{background: radial-gradient(50% 10px at center bottom, transparent 100%,#FFE8A3 0) center bottom;
}
效果如下(全部都是径向渐变绘制)

当然你也可以随意改变径向的弧度和大小,来实现各种不同的效果。
以上所有demo都可以查看以下在线链接
- CSS radius layout (codepen.io)
四、优缺点总结
以上就是本文的全部内容了,共介绍了 3 种不同的方式,下面总结一下各自优缺点
- border-radius 支持斜杠语法,可以单独控制圆弧的x、y半径,实现“外凸”圆弧最简单,缺点是圆弧不能自定义弧度,也不能实现“内凹”效果
- 伪元素最符合常规思维,可以解决以上问题,缺点是需要占用伪元素,略微麻烦
- 渐变实现和伪元素拼接思路类似,缺点是语法复杂,需要熟练掌握渐变语法
学习资料:点此下载
相关文章:

用CSS制作弧形卡片的三种创意方法!
在平时开发中,有时候会碰到下面这种“弧形”样式,主要分为“内凹”和“外凸”两种类型,如下 该如何实现呢?或者想一下,有哪些 CSS 属性和“弧形”有关?下面介绍 3 种方式,一起看看吧 一、borde…...

守护健康之光 —— 小脑萎缩患者的生活指南
生活中,我们或许会遇到一些特殊的挑战,而面对这些挑战时,了解和掌握正确的应对策略至关重要。今天,我们要聊一聊一个较为少见却不容忽视的话题——小脑萎缩。这不仅是患者的战役,也是家人和社会共同的关怀课题。下面&a…...

CSS选择器:让样式精确命中目标
CSS选择器:让样式精确命中目标 在网页开发中,CSS选择器是一种强大的工具,它可以帮助我们精确地定位HTML元素,以便为它们应用样式。在这篇博客中,我们将探讨一些常见的CSS选择器,了解它们的功能和使用方法。…...

前端不传被删记录的id怎么删除记录,或子表如何删除记录
1.删除主表相关子表所有记录 2.再保存一次前端传来的记录 3.如果子表是通过先生成空记录,再put修改模式,可以在执行1和2两步后再拿模板集合和当前现有子表集合套两个for循环对比判断,count记录模板记录和子表记录每次循环重合次数ÿ…...

axios的基本特性用法
1. axios的基本特性 axios 是一个基于Promise用于浏览器和node.js的HTTP客户端。 它具有以下特征: 支持浏览器和node.js支持promiseAPI自动转换JSON数据能拦截请求和响应请求转换请求数据和响应数据(请求是可以加密,在返回时也可进行解密&…...
打印水仙花数---c语言刷题
欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎指出~ 题述 求出0~100000之间的所有“水仙花数”并输出。 “水仙花数”是指一个n位数,其各位数字的n次方之和确好等于该数本身,如:153&#…...
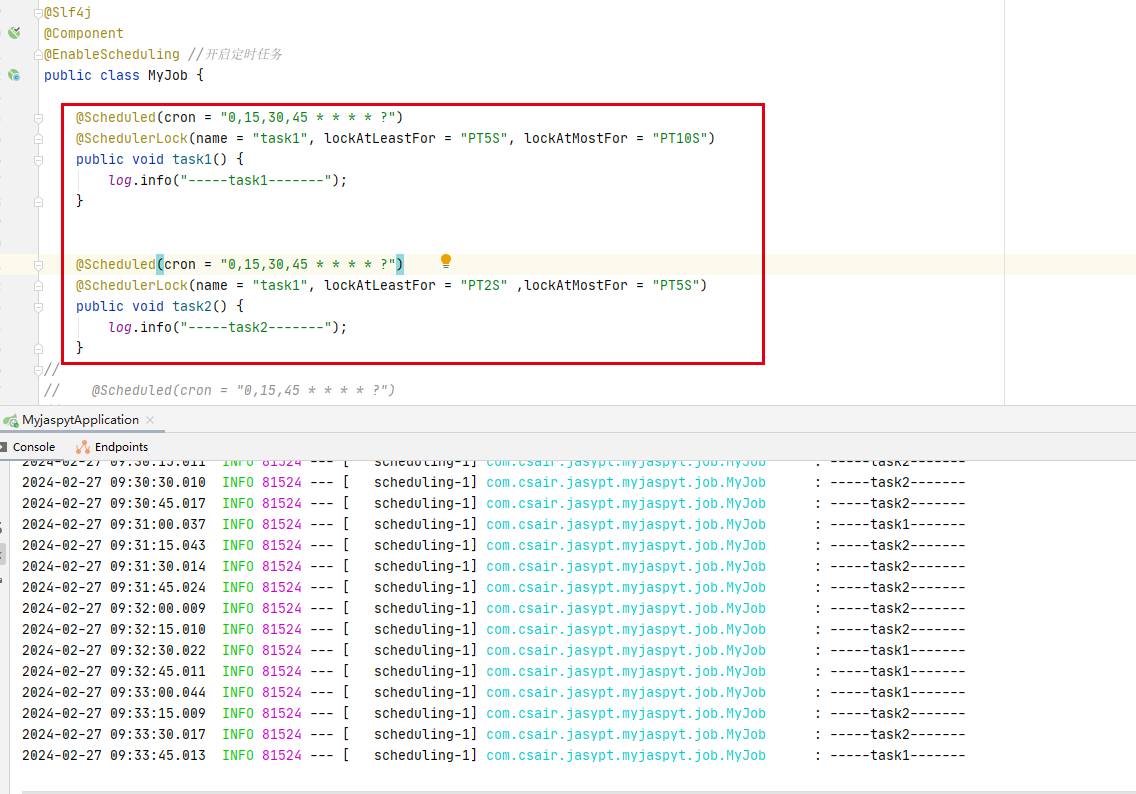
springboot基础(82):分布式定时任务解决方案shedlock
文章目录 前言简介shedlock dbSchedulerLock注解说明 shedlock redis遇到的问题1.配置shedlock不生效2.报错net/javacrumbs/shedlock/core/LockProvider shedlock升级高版本同名定时任务 前言 多节点或者多服务器拥有相同的定时任务,这种情况下,不同节…...

【Golang】Gorm乐观锁optimisticlock的使用
在数据库操作中,为了保证数据的一致性和完整性,常常需要采取一些措施来防止并发操作导致的数据冲突。悲观锁和乐观锁是两种常见的并发控制机制。 悲观锁(Pessimistic Lock) 悲观锁的基本假设是,数据在并发访问时很可能…...

Apache Doris 发展历程、技术特性及云原生时代的未来规划
本文节选自《基础软件之路:企业级实践及开源之路》一书,该书集结了中国几乎所有主流基础软件企业的实践案例,由 28 位知名专家共同编写,系统剖析了基础软件发展趋势、四大基础软件(数据库、操作系统、编程语言与中间件…...
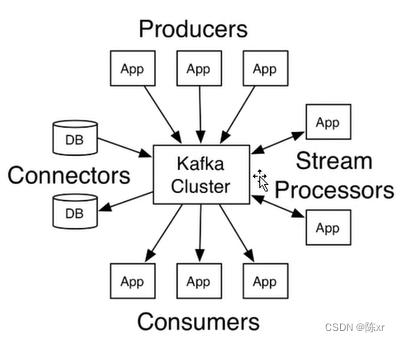
2024-02-26(Spark,kafka)
1.Spark SQL是Spark的一个模块,用于处理海量结构化数据 限定:结构化数据处理 RDD的数据开发中,结构化,非结构化,半结构化数据都能处理。 2.为什么要学习SparkSQL SparkSQL是非常成熟的海量结构化数据处理框架。 学…...

RubyMine 2023:让Ruby编程变得更简单 mac/win版
JetBrains RubyMine 2023是一款专为Ruby开发者打造的强大集成开发环境(IDE)。这款工具集成了许多先进的功能,旨在提高Ruby编程的效率和生产力。 RubyMine 2023软件获取 RubyMine 2023的智能代码编辑器提供了丰富的代码补全和提示功能&#…...
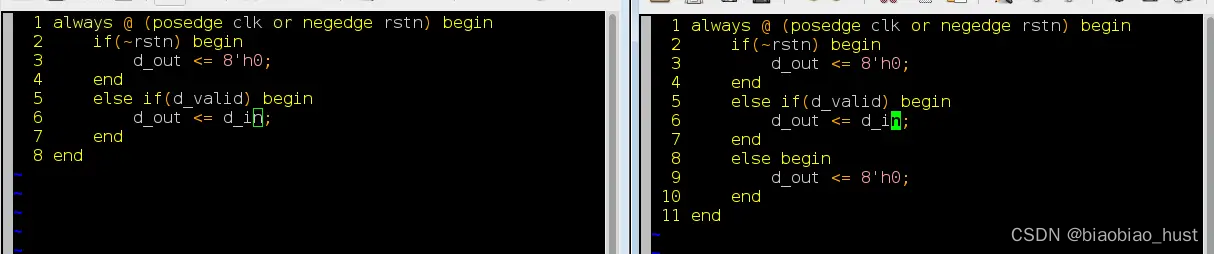
低功耗设计——门控时钟
1. 前言 芯片功耗组成中,有高达40%甚至更多是由时钟树消耗掉的。这个结果的原因也很直观,因为这些时钟树在系统中具有最高的切换频率,而且有很多时钟buffer,而且为了最小化时钟延时,它们通常具有很高的驱动强度。此外&…...

《凤凰架构》-本地事务章节 读书笔记
1、写锁又名排它锁,写锁禁止其他事务施加读锁和写锁,而不禁止其他事务读取数据(如果遇到了个不加任何锁的另一个事务2,写锁是无法阻止事务2读取数据的),这就是读未提交隔离级别中的脏读问题产生的根因。 2…...

ruby对比python,30分钟教程
会python还需要搞会ruby吗? web方面:ruby有rails,python有flask,django,rails远超django Ruby,一种简单快捷的面向对象(面向对象程序设计)脚本语言,在20世纪90年代由日本人松本行弘…...

C语言——oj刷题——判断闰年
当我们谈到判断闰年时,我们通常会遵循以下规则:闰年是指能被4整除但不能被100整除的年份,或者能被400整除的年份。在C语言中,我们可以通过编写一个简单的程序来实现这一功能。下面是一个示例代码,用于判断一个给定年份…...
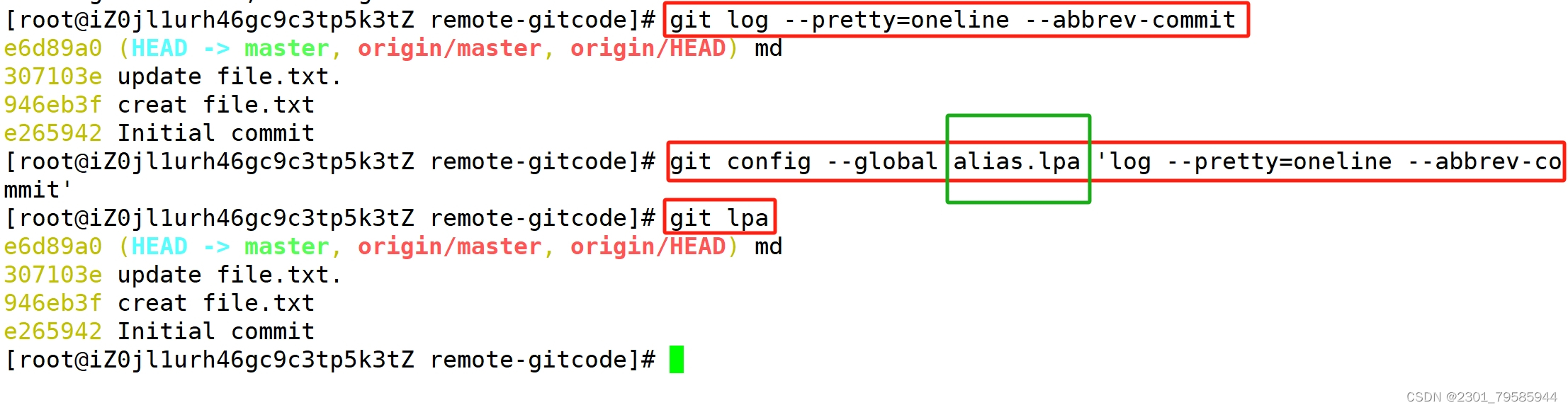
Git笔记——3
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 一、合并模式和分支策略 二、bug分支 三、强制删除分支 四、创建远程仓库 五、克隆远程仓库_HTTPS和_SSH 克隆远程仓库_HTTPS 克隆远程仓库_SSH 六、向远程仓库…...

C++面试 -操作系统-安全能力:死锁的危害、出现原因、解决方法
目录 死锁的危害 死锁出现的原因 死锁的解决方法 死锁是计算机科学中一个非常重要的概念,特别是在多线程、并发编程以及数据库管理系统等领域中。下面是关于死锁的危害、出现原因和解决方法的基础概述: 死锁的危害 资源浪费:死锁导致系统…...

台湾香港澳门媒体宣发稿报道有哪些平台资源,跨境出海推广新闻营销公司告诉你
【本篇由言同数字科技有限公司原创】随着全球化的快速发展和互联网的普及,品牌越来越重视海外市场的开拓。作为亚洲地区的重要经济中心,香港、台湾和澳门不仅具有独特的地理位置和文化背景,还拥有丰富的媒体资源。在本文中,我们将…...

Python分支和循环结构及其应用(文末送书)
一、分支结构 应用场景 我们写的Python代码都是一条一条语句顺序执行,这种代码结构通常称之为顺序结构。然而仅有顺序结构并不能解决所有的问题。 if语句的使用 在Python中,要构造分支结构可以使用if、elif和else关键字。所谓关键字就是有特殊含义的…...

机器学习——线性代数中矩阵和向量的基本介绍
矩阵和向量的基本概念 矩阵的基本概念(这里不多说,应该都知道) 而向量就是一个特殊的矩阵,即向量只有一列,是个n*1的矩阵 注:一般矩阵用大写字母表示,向量用小写字母表示 矩阵的加减运算 两个…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
