机器学习——线性代数中矩阵和向量的基本介绍
矩阵和向量的基本概念
矩阵的基本概念（这里不多说，应该都知道）
而向量就是一个特殊的矩阵，即向量只有一列，是个n*1的矩阵
注：一般矩阵用大写字母表示，向量用小写字母表示
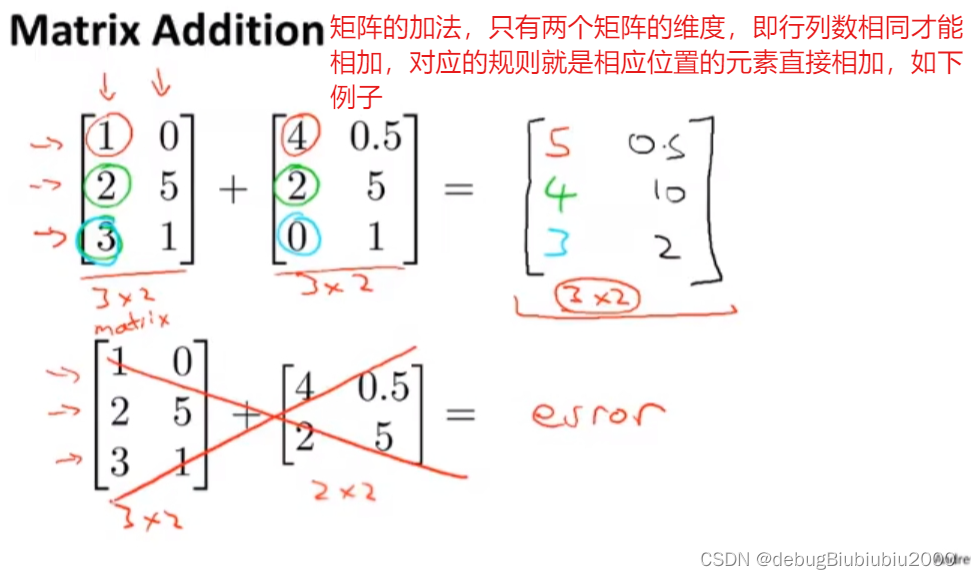
矩阵的加减运算
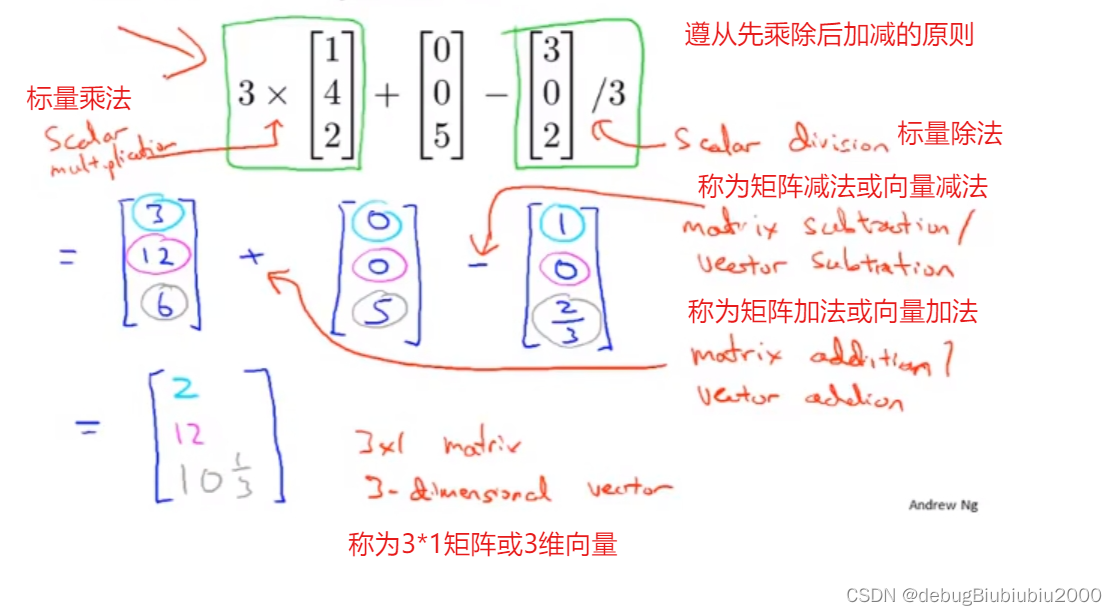
两个矩阵的乘法
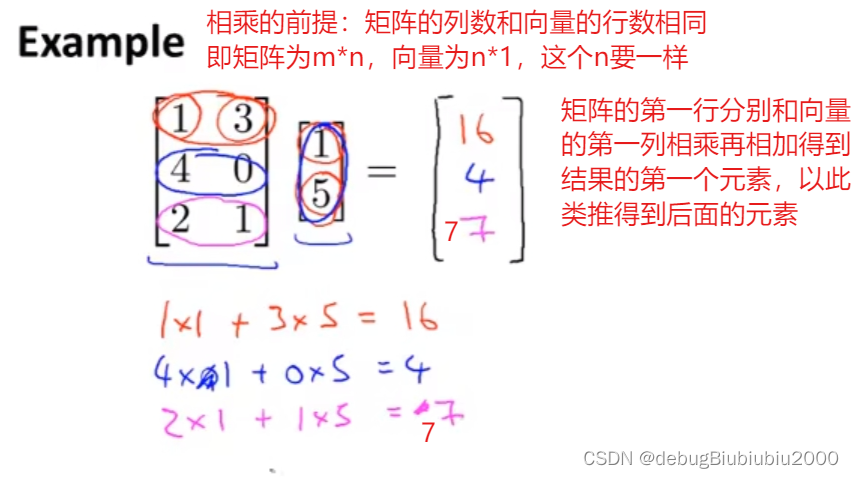
矩阵向量相乘
先从简单开始，即一个矩阵和一个向量相乘的运算
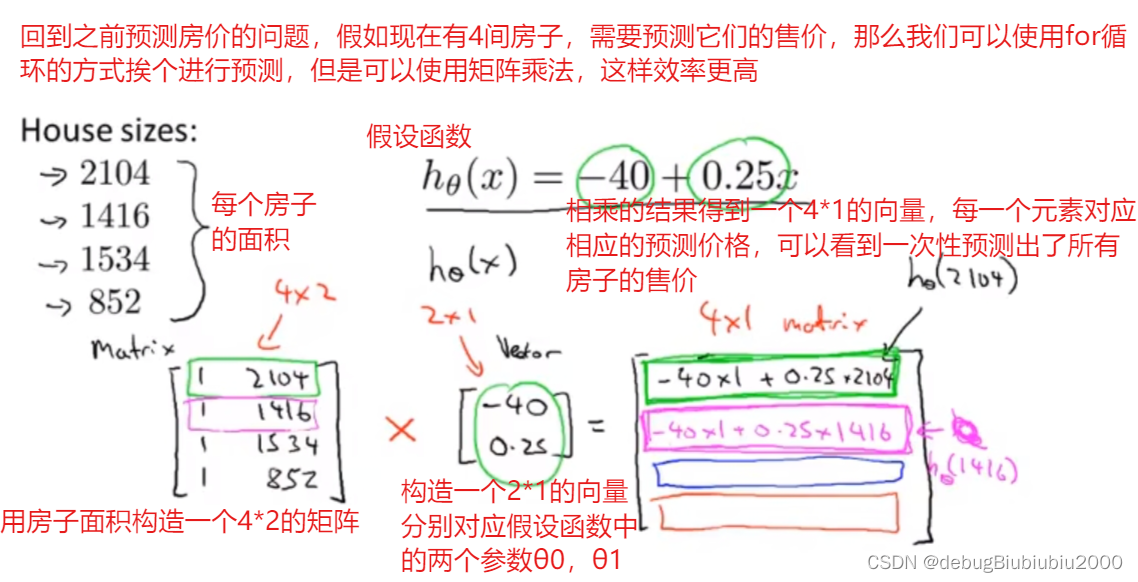
矩阵向量相乘在机器学习中的应用
两个矩阵相乘
矩阵相乘的结果的维度为m*k
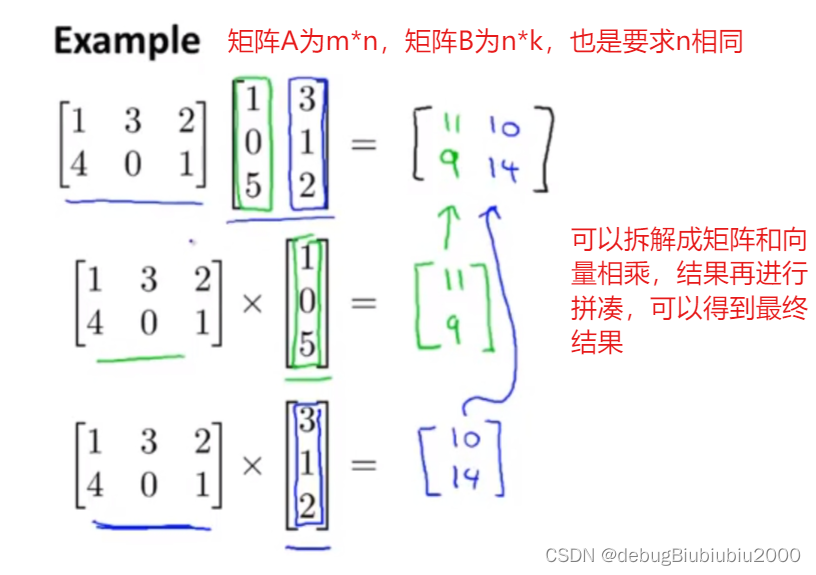矩阵相乘的应用
矩阵乘法的一些特性
矩阵乘法满足结合律不满足交换律（当有一个矩阵是单位矩阵时满足交换律）
单位矩阵的基本概念
矩阵的逆运算和矩阵的转置
矩阵的逆
在实数中，一个数乘以它的倒数等于1，类似的，一个矩阵A乘以另一个矩阵得到单位矩阵，那么这个矩阵就称为矩阵A的逆矩阵，如下定义
注意：
- 只有方阵才有逆矩阵
- 类似于0没有倒数，所以不是所有的矩阵都有逆矩阵，不存在逆矩阵的矩阵称为奇异矩阵或退化矩阵
至于如何求矩阵的逆（可以用数学的方法计算，也可以用编程实现），如何判断一个矩阵有没有逆矩阵等这里不进行介绍，可以自行百度
矩阵的转置
相关文章：
机器学习——线性代数中矩阵和向量的基本介绍
矩阵和向量的基本概念 矩阵的基本概念（这里不多说，应该都知道） 而向量就是一个特殊的矩阵，即向量只有一列，是个n*1的矩阵 注：一般矩阵用大写字母表示，向量用小写字母表示 矩阵的加减运算 两个…...
基于R语言的Meta分析【全流程、不确定性分析】方法与Meta机器学习技术应用
Meta分析是针对某一科研问题，根据明确的搜索策略、选择筛选文献标准、采用严格的评价方法，对来源不同的研究成果进行收集、合并及定量统计分析的方法，最早出现于“循证医学”，现已广泛应用于农林生态，资源环境等方面。…...
蜘蛛蜂优化算法SWO求解不闭合MD-MTSP，可以修改旅行商个数及起点（提供MATLAB代码）
1、蜘蛛蜂优化算法SWO 蜘蛛蜂优化算法（Spider wasp optimizer，SWO）由Mohamed Abdel-Basset等人于2023年提出，该算法模型雌性蜘蛛蜂的狩猎、筑巢和交配行为，具有搜索速度快，求解精度高的优势。VRPTW&#x…...
Java架构师之路六、高并发与性能优化：高并发编程、性能调优、线程池、NIO、Netty、高性能数据库等。
目录 高并发编程： 性能调优： 线程池： NIO： Netty： 高性能数据库： 上篇：Java架构师之路五、微服务：微服务架构、服务注册与发现、服务治理、服务监控、容器化等。-CSDN博客 下篇…...
MySQL-行转列，链接查询
1. 行转列 1.1 示例数据准备 create table test_9(id int,name varchar(22),course varchar(22),score decimal(18,2) ); insert into test_9 (id,name,course,score)values(1,小王,java,99); insert into test_9 (id,name,course,score)values(2,小张,java,89.2); inse…...
Linux之安装jdk，tomcat，mysql，部署项目
目录 一、操作流程 1.1安装jdk 1.2安装tomcat（加创建自启动脚本） 1.3 安装mysql 1.4部署项目 一、操作流程 首先把需要用的包放进opt文件下 1.1安装jdk 把jdk解压到/usr/local/java里 在刚刚放解压包的文件夹打开vim /etc/profile编辑器，…...
HTMLElement.click()的回调触发踩坑
先看看以下代码 const el document.getElementById("btn") el.addEventListener("click", () > {Promise.resolve().then(() > console.log("microtask 1"));console.log("1"); }); el.addEventListener("click", (…...
mysql锁-这条sql加了哪些锁
文章目录 1、 InnoDB的三种行锁2、常见的加锁语句2.1、常见隐式加锁语句2.1、常见显示加锁语句 3、加锁的2条规则4、案例4.1、唯一索引等值查询4.2、唯一索引范围查询4.3、非唯一索引等值查询4.4、非唯一索引范围查询 InnoDB 存储引擎中的行锁的加锁规则。 1、 InnoDB的三种行锁…...
Docusaurus框架——快速搭建markdown文档站点介绍sora
文章目录 ⭐前言⭐初始化项目💖 创建项目（react-js）💖 运行项目💖 目录文件💖 创建一个jsx页面💖 创建一个md文档💖 创建一个介绍sora的文档 ⭐总结⭐结束 ⭐前言 大家好࿰…...
Prompt 编程的优化技巧
一、为什么要优化 一）上下文限制 目前 GPT-3.5 以及 GPT-4最大支持 16K 上下文，比如你输入超过 16k 的长文本，ChatGPT 会提示文本过大，为了避免 GPT 无法回复，需要限制 上下文在16k 以内 上下文对于 GPT 来说是非常重…...
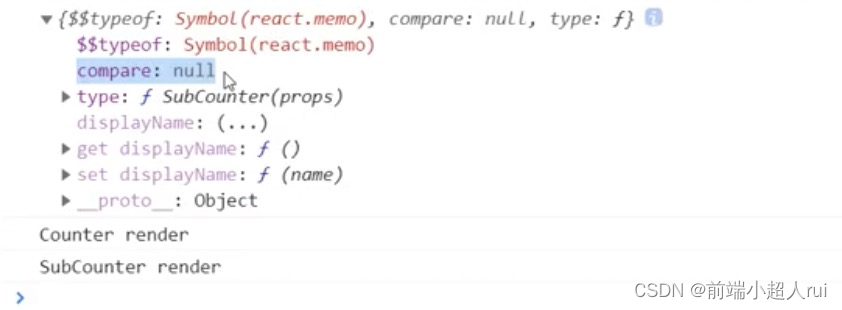
React PureComponent 和 React.memo()区别
1 注意 ● PureComponent和memo仅作为性能优化的方式存在 ● 不要依赖它来阻止渲染，会产生BUG ● PureComponnet 和memo 都是通过对 props 值的浅比较来决定该组件是否需要更新的。 2 PureComponent 和React.memo() 区别 PureComponent 和React.memo()都是React优化…...
CentOS 7全系列免费
CentOS 7 全系列免费：桌面版、工作站版、服务器版等等………… 上文，关于CentOS 7这句话，被忽略了。 注意版本：知识产权、网络安全。...
【Spring连载】使用Spring Data访问 MongoDB----Aggregation Framework支持
【Spring连载】使用Spring Data访问 MongoDB----聚合框架支持 一、基础槪念二、投影表达式Projection Expressions三、分面分类法Faceted Classification3.1 桶Buckets3.2 多方面的聚合Multi-faceted Aggregation3.3 按计数排序Sort By Count3.4 投影表达式中的Spring表达式支持…...
【深入理解设计模式】适配器设计模式
适配器设计模式 适配器设计模式是一种结构型设计模式，用于将一个类的接口转换成客户端所期望的另一个接口，从而使得原本由于接口不兼容而不能一起工作的类能够一起工作。适配器模式通常用于以下场景： 现有接口与需求不匹配：当需要…...
ASP.NET-实现图形验证码
ASP.NET 实现图形验证码能够增强网站安全性，防止机器人攻击。通过生成随机验证码并将其绘制成图像，用户在输入验证码时增加了人机交互的难度。本文介绍了如何使用 C# 和 ASP.NET 创建一个简单而有效的图形验证码系统，包括生成随机验证码、绘制…...
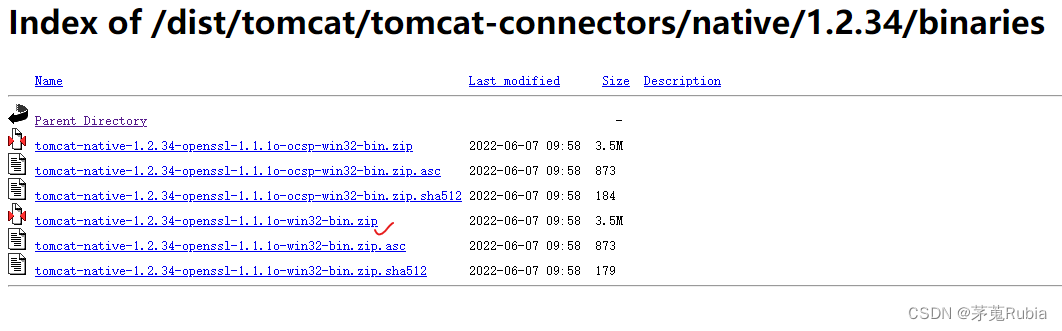
解决Maven爆红以及解决 Idea 卡在 Resolving问题
关于 Idea 卡在 Resolving（前提是Maven的setting.xml中配置好了阿里云和仓库） 参考文章https://blog.csdn.net/jiangyu1013/article/details/95042611 解决Maven爆红参考文章https://devpress.csdn.net/beijing/656d993b76f0791b6eca7bb0.html?dp_toke…...
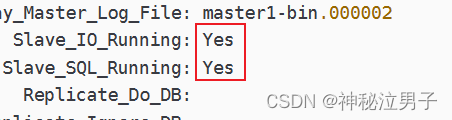
MySQL集群 双主架构（配置命令）
CSDN 成就一亿技术人！ 今天刚开学第一天给大家分享一期：MySQL集群双主的配置需求和命令 CSDN 成就一亿技术人！ 神秘泣男子主页：作者首页 <———— MySQL专栏 ：MySQL数据库专栏<———— MySQL双主是一…...
网络安全之安全事件监测
随着人们对技术和智能互联网设备依赖程度的提高，网络安全的重要性也在不断提升。因此，我们需要不断加强网络安全意识和措施，确保网络环境的安全和稳定。 网络安全的重要性包含以下几点： 1、保护数据安全：数据是组织和…...
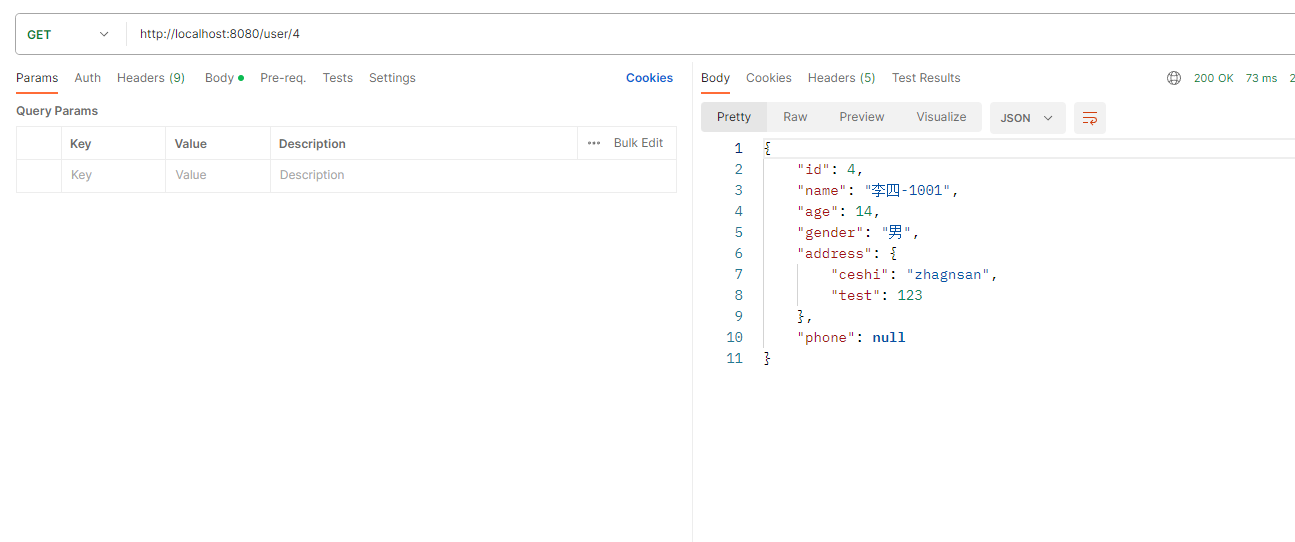
【BUG 记录】MyBatis-Plus 处理枚举字段和 JSON 字段
【BUG 记录】MyBatis-Plus 处理枚举字段和JSON字段 一、枚举字段（mysql环境已测、postgresql环境已测）1.1 场景1.2 定义枚举常量1.3 配置枚举处理器1.4 测试 二、JSON字段（mysql环境已测）2.1 导包2.2 使用对象接受2.3 测试 三、JS…...
Web性能优化-详细讲解与实用方法-MDN文档学习笔记
Web性能优化 查看更多学习笔记：GitHub：LoveEmiliaForever MDN中文官网 性能优良的网站能够提高访问者留存和用户满意度，减少客户端和服务器之间传输的数据量可降低各方的成本 不同的业务目标和用户需求需要不同的性能度量，要提高…...
Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向： 逆向设计 通过神经网络快速预测微纳结构的光学响应，替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
: K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？)
云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？
大家好，欢迎来到《云原生核心技术》系列的第七篇！ 在上一篇，我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在，我们就像一个拥有了一块崭新数字土地的农场主，是时…...
Java如何权衡是使用无序的数组还是有序的数组
在 Java 中，选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南： ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式（Python 实现） 在 Python 中，你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是，.doc 是旧的 Word 格式，而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息，但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN，但是…...
Caliper 配置文件解析：config.yaml
Caliper 是一个区块链性能基准测试工具，用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构，并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件，主要包含以下几个部…...
AI书签管理工具开发全记录（十九）：嵌入资源处理
1.前言 📝 在上一篇文章中，我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源，方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包，彻底改变了静态资源管理的…...
Aspose.PDF 限制绕过方案：Java 字节码技术实战分享（仅供学习）
Aspose.PDF 限制绕过方案：Java 字节码技术实战分享（仅供学习） 一、Aspose.PDF 简介二、说明（⚠️仅供学习与研究使用）三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...