神经网络系列---归一化
文章目录
- 归一化
- 批量归一化
- 预测阶段
- 测试阶段
- γ和β(注意)
- 举例
- 层归一化
- 前向传播
- 反向传播
归一化
批量归一化
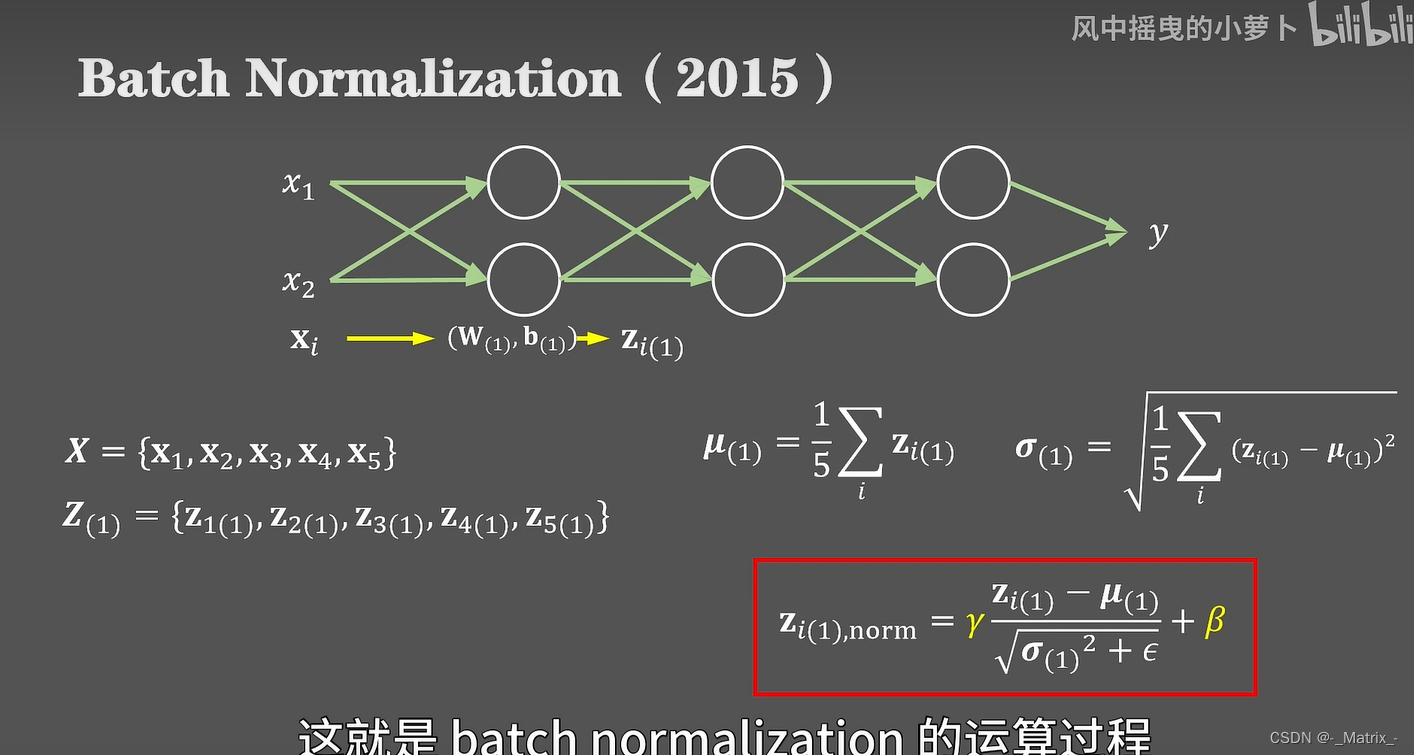


(Batch Normalization)在训练过程中的数学公式可以概括如下:
给定一个小批量数据 B = { x 1 , x 2 , … , x m } B = \{x_1, x_2, \ldots, x_m\} B={x1,x2,…,xm},其中 m m m 是批次的大小。
-
计算均值:计算小批量数据的均值。
μ B = 1 m ∑ i = 1 m x i \mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i μB=m1∑i=1mxi -
计算方差:计算小批量数据的方差。
σ B 2 = 1 m ∑ i = 1 m ( x i − μ B ) 2 \sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 σB2=m1∑i=1m(xi−μB)2 -
归一化:使用均值和方差对小批量数据进行标准化。
x ^ i = x i − μ B σ B 2 + ϵ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} x^i=σB2+ϵxi−μB
其中, ϵ \epsilon ϵ 是一个小的常数,用于确保分母不为零。 -
缩放和平移:使用可学习的参数伽玛 γ \gamma γ和贝塔 β \beta β来缩放和平移标准化的数据。
y i = γ x ^ i + β y_i = \gamma \hat{x}_i + \beta yi=γx^i+β
其中, γ \gamma γ 和 β \beta β 是可学习的参数,用于调整归一化的缩放和平移。
这样做可以让模型有更大的灵活性,因为它可以学习到每个特征或通道应该如何被归一化。
预测阶段
在推断阶段,使用整个训练集的均值和方差(通常是移动平均)来替代小批量的均值和方差。这确保了网络在推断时的行为与训练时的行为更加一致。
在批量归一化中,移动平均均值和方差是在训练阶段计算并用于预测阶段的归一化过程。移动平均的计算通常使用指数移动平均(EMA)或其他平滑方法。下面是计算移动平均均值和方差的一般过程:
-
初始化:在训练开始时,初始化移动平均均值和方差为零或其他初始值。
-
计算当前批次的均值和方差:对于每个训练批次,计算该批次数据的均值和方差。
-
更新移动平均:使用当前批次的均值和方差以及之前的移动平均值来更新移动平均。通常,这可以通过下面的公式完成:
移动平均均值 = m o m e n t u m × 移动平均均值 + ( 1 − m o m e n t u m ) × 当前批次均值 \text{移动平均均值} = momentum \times \text{移动平均均值} + (1 - momentum) \times \text{当前批次均值} 移动平均均值=momentum×移动平均均值+(1−momentum)×当前批次均值
移动平均方差 = m o m e n t u m × 移动平均方差 + ( 1 − m o m e n t u m ) × 当前批次方差 \text{移动平均方差} = momentum \times \text{移动平均方差} + (1 - momentum) \times \text{当前批次方差} 移动平均方差=momentum×移动平均方差+(1−momentum)×当前批次方差其中, m o m e n t u m momentum momentum 是一个超参数,通常在 0 到 1 之间,通常设置为接近 1 的值(例如 0.9),决定了移动平均的平滑程度。较小的 m o m e n t u m momentum momentum 值会使移动平均更关注最近的批次,而较大的值则会使其更平滑。
-
使用当前mini-batch的均值和方差对数据进行归一化,并通过可学习的参数 γ γ γ 和 β β β 进行缩放和偏移。
BN ( x i ) = γ ( x i − μ B σ B 2 + ϵ ) + β \text{BN}(x_i) = \gamma \left( \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \right) + \beta BN(xi)=γ(σB2+ϵxi−μB)+β
测试阶段
在测试阶段,使用训练期间计算的运行均值和方差进行归一化:
BN ( x i ) = γ ( x i − μ running σ running 2 + ϵ ) + β \text{BN}(x_i) = \gamma \left( \frac{x_i - \mu_{\text{running}}}{\sqrt{\sigma_{\text{running}}^2 + \epsilon}} \right) + \beta BN(xi)=γ(σrunning2+ϵxi−μrunning)+β
通过这种方式,批量归一化可以在测试阶段更稳定和准确地归一化数据。
γ和β(注意)
在批量归一化中, γ \gamma γ 和 β \beta β 不是单一的数值,而是可以学习的参数向量。其维度与正在被归一化的数据的维度相同。这样可以确保每个特征有其自己的 γ \gamma γ 和 β \beta β 参数,可以独立地进行缩放和偏移。
具体来说:
- 在全连接层中,如果该层有 d d d 个神经元,那么 γ \gamma γ 和 β \beta β 将是 d d d 维向量。
- 在卷积层中,如果卷积层有 c c c 个通道,那么 γ \gamma γ 和 β \beta β 将是 c c c 维向量,每个通道有一个 γ \gamma γ 和 β \beta β 值。
举例
以下是按照10个样本,20个特征,计算移动平均方差的步骤:
-
初始化移动平均方差:在训练开始时,为每个特征初始化一个移动平均方差值。可以将其设置为零或其他初始值。你将得到一个具有20个元素的移动平均方差向量。
-
对于每个批次:对于每个训练批次,执行以下步骤:
a. 计算当前批次的方差:按照之前的方法计算当前批次的方差。结果将是一个包含20个方差值的向量。
b. 更新移动平均方差:使用以下公式来更新每个特征的移动平均方差:
移动平均方差 j = m o m e n t u m × 移动平均方差 j + ( 1 − m o m e n t u m ) × 当前批次方差 j \text{移动平均方差}_j = momentum \times \text{移动平均方差}_j + (1 - momentum) \times \text{当前批次方差}_j 移动平均方差j=momentum×移动平均方差j+(1−momentum)×当前批次方差j
其中, m o m e n t u m momentum momentum 是一个超参数,通常在 0 到 1 之间,表示移动平均的平滑程度。这个过程会为每个特征更新移动平均方差。
- 预测时使用:在预测阶段,使用最终计算的移动平均方差向量来归一化新样本。
在批量归一化中,每个特征都有其自己的移动平均均值和移动平均方差。这些值是在训练过程中单独计算和跟踪的。
由于不同的特征可能具有不同的尺度和分布,因此为每个特征单独计算均值和方差是有意义的。这样可以确保在整个训练集中,每个特征都被归一化到具有相同的均值和方差,从而有助于提高训练的稳定性和效率。
层归一化
(Layer Normalization)是一种归一化技术,常用于深度学习模型中。下面我们来详细了解层归一化的前向传播和反向传播过程。
前向传播
给定输入向量 x x x,层归一化的前向传播包括以下步骤:
-
计算均值:计算输入 x x x 中所有特征的均值。
μ = 1 d ∑ i = 1 d x i \mu = \frac{1}{d} \sum_{i=1}^{d} x_i μ=d1∑i=1dxi -
计算方差:计算输入 x x x 中所有特征的方差。
σ 2 = 1 d ∑ i = 1 d ( x i − μ ) 2 \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 σ2=d1∑i=1d(xi−μ)2 -
归一化:使用均值和方差对输入 x x x 进行标准化。
x ^ i = x i − μ σ 2 + ϵ \hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} x^i=σ2+ϵxi−μ -
缩放和平移:使用可学习的参数伽玛 γ \gamma γ和贝塔 β \beta β来缩放和平移标准化的数据。
y i = γ x ^ i + β y_i = \gamma \hat{x}_i + \beta yi=γx^i+β
反向传播
反向传播需要计算损失函数 L L L 对输入 x x x、伽玛 γ \gamma γ和贝塔 β \beta β的偏导数。以下是相关的偏导数计算:
-
对伽玛和贝塔的偏导数:
∂ L ∂ γ = ∑ i = 1 d ∂ L ∂ y i x ^ i , ∂ L ∂ β = ∑ i = 1 d ∂ L ∂ y i \frac{\partial L}{\partial \gamma} = \sum_{i=1}^{d} \frac{\partial L}{\partial y_i} \hat{x}_i, \quad \frac{\partial L}{\partial \beta} = \sum_{i=1}^{d} \frac{\partial L}{\partial y_i} ∂γ∂L=∑i=1d∂yi∂Lx^i,∂β∂L=∑i=1d∂yi∂L -
对归一化输入的偏导数:
∂ L ∂ x ^ i = ∂ L ∂ y i γ \frac{\partial L}{\partial \hat{x}_i} = \frac{\partial L}{\partial y_i} \gamma ∂x^i∂L=∂yi∂Lγ -
对方差的偏导数:
∂ L ∂ σ 2 = 1 2 ∑ i = 1 d ∂ L ∂ x ^ i 1 σ 2 + ϵ ( x i − μ ) \frac{\partial L}{\partial \sigma^2} = \frac{1}{2} \sum_{i=1}^{d} \frac{\partial L}{\partial \hat{x}_i} \frac{1}{\sqrt{\sigma^2 + \epsilon}} (x_i - \mu) ∂σ2∂L=21∑i=1d∂x^i∂Lσ2+ϵ1(xi−μ) -
对均值的偏导数:
∂ L ∂ μ = ∑ i = 1 d ∂ L ∂ x ^ i − 1 σ 2 + ϵ − 2 d ∂ L ∂ σ 2 ( μ − x i ) \frac{\partial L}{\partial \mu} = \sum_{i=1}^{d} \frac{\partial L}{\partial \hat{x}_i} \frac{-1}{\sqrt{\sigma^2 + \epsilon}} - \frac{2}{d} \frac{\partial L}{\partial \sigma^2} (\mu - x_i) ∂μ∂L=∑i=1d∂x^i∂Lσ2+ϵ−1−d2∂σ2∂L(μ−xi) -
对输入的偏导数:
∂ L ∂ x i = ∂ L ∂ x ^ i 1 σ 2 + ϵ + 2 d ∂ L ∂ σ 2 ( x i − μ ) + 1 d ∂ L ∂ μ \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial \hat{x}_i} \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \frac{2}{d} \frac{\partial L}{\partial \sigma^2} (x_i - \mu) + \frac{1}{d} \frac{\partial L}{\partial \mu} ∂xi∂L=∂x^i∂Lσ2+ϵ1+d2∂σ2∂L(xi−μ)+d1∂μ∂L
这些偏导数可以通过链式法则和上述前向传播步骤计算,从而实现层归一化的反向传播。这样就可以在训练过程中更新模型参数,并通过梯度下降或其他优化算法进行优化。
相关文章:

神经网络系列---归一化
文章目录 归一化批量归一化预测阶段 测试阶段γ和β(注意)举例 层归一化前向传播反向传播 归一化 批量归一化 (Batch Normalization)在训练过程中的数学公式可以概括如下: 给定一个小批量数据 B { x 1 , x 2 , … …...

2023 龙蜥操作系统大会演讲实录:《兼容龙蜥的云原生大模型数据计算系统——πDataCS》
本文主要分三部分内容:第一部分介绍拓数派公司,第二部分介绍 πDataCS 产品,最后介绍 πDataCS 与龙蜥在生态上的合作。 杭州拓数派科技发展有限公司(简称“拓数派”,英文名称“OpenPie”)是国内基础数据计…...

【Vue渗透】Vue站点渗透思路
原文地址 极核GetShell 前言 本文经验适用于前端用Webpack打包的Vue站点,阅读完本文,可以识别出Webpack打包的Vue站点,同时可以发现该Vue站点的路由。 成果而言:可能可以发现未授权访问。 识别Vue 识别出Webpack打包的Vue站…...

主数据管理是数字化转型成功的基石——江淮汽车案例分享
汽车行业数字化转型的背景 在新冠疫情导火索的影响下,经济全球化政治基础逐渐动摇。作为全球最大的汽车市场,我国的汽车市场逐渐由增量转为存量市场。 在数字化改革大背景下,随着工业4.0时代的到来,江淮汽车集团力争实现十四五数…...
----加密Encryption (CSFLE))
【Spring连载】使用Spring Data访问 MongoDB(十一)----加密Encryption (CSFLE)
[TOC](【Spring连载】使用Spring Data访问 MongoDB(十一)----加密Encryption (CSFLE)) 一级目录 二级目录 三级目录...
【postgresql】数据表id自增与python sqlachemy结合实例
需求: postgresql实现一个建表语句,表名:student,字段id,name,age, 要求:每次添加一个数据id会自动增加1 在PostgreSQL中,您可以使用SERIAL或BIGSERIAL数据类型来自动生成主键ID。以下是一个创建名为stude…...

什么是索引?在 MySQL 中有哪些类型的索引?它们各自的优势和劣势是什么?
什么是索引?在 MySQL 中有哪些类型的索引?它们各自的优势和劣势是什么? 索引是数据库中用于帮助快速查询数据的一种数据结构。在 MySQL 中,索引可以显著提高查询性能,因为它允许数据库系统不必扫描整个表来找到相关数据…...

Docker安装与基础知识
目录 -----------------Docker 概述--------------------------- 容器化越来越受欢迎,因为容器是: Docker与虚拟机的区别: Docker核心概念: ●镜像 ●容器 ●仓库 -----------------安装 Docker--------------------------…...
搭建Facebook直播网络对IP有要求吗?
在当今数字化时代,Facebook直播已经成为了一种极具吸引力的社交形式,为个人和企业提供了与观众直接互动的机会,成为推广产品、分享经验、建立品牌形象的重要途径。然而,对于许多人来说,搭建一个稳定、高质量的Facebook…...
Qt开发:MAC安装qt、qtcreate(配置桌面应用开发环境)
安装qt-creator brew install qt-creator安装qt brew install qt查看qt安装路径 brew info qtzhbbindembp ~ % brew info qt > qt: stable 6.6.1 (bottled), HEAD Cross-platform application and UI framework https://www.qt.io/ /opt/homebrew/Cellar/qt/6…...

python学习网站
Python系列干货之——Python与设计模式 - 知乎 Python之23种设计模式_23种设计模式 python-CSDN博客 用python实现设计模式 — python-golang-web-guide 0.1 文档 python设计模式_Python六大原则,23种设计模式 - 掘金 Python 常用设计模式 Python入门 类class提…...

编程笔记 Golang基础 033 反射的类型与种类
编程笔记 Golang基础 033 反射的类型与种类 一、反射的类型和种类二、切片与反射三、集合与反射四、结构体与反射五、指针与反射六、函数与反射小结 反射机制的作用范围涵盖了几乎所有的类型和值的操作层面,它极大地增强了Go语言在运行时对于自身类型系统的探索和操…...
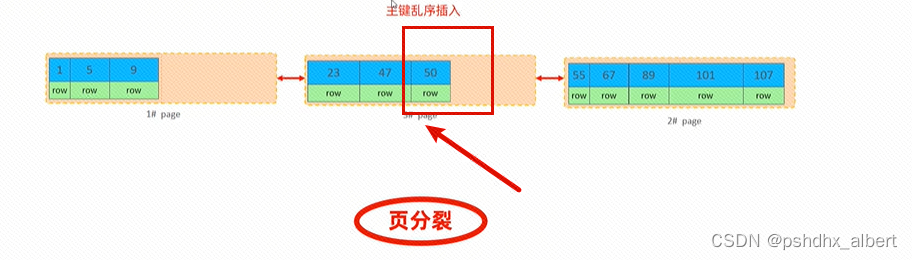
MySQL进阶篇2-索引的创建和使用以及SQL的性能优化
索引 mkdir mysql tar -xvf mysqlxxxxx.tar -c myql cd mysql rpm -ivh .....rpm yum install openssl-devel systemctl start mysqld gerp temporary password /var/log/mysqld.log mysql -u root -p mysql> show variables like validate_password.% set glob…...

基于SVM的功率分类,基于支持向量机SVM的功率分类识别,Libsvm工具箱详解
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 完整代码和数据下载链接:基于SVM的功率分类,基于支持向量机SVM的功率分类识别资源-CSDN文库 https://download.csdn.net/download/abc991835105/88862836 SVM应用实例, 基于…...
【IO流】FileWrite字符输出流
FileWrite字符输出流 1. 概述2. 作用3. 方法4. 细节5. 代码示例6. 注意事项 1. 概述 java.io.FileWriter 类是写出字符到文件的便利类。构造时使用系统默认的字符编码和默认字节缓冲区。 FileWriter 是用于写入字符数据到文件的字符输出流。 2. 作用 写入字符数据:…...
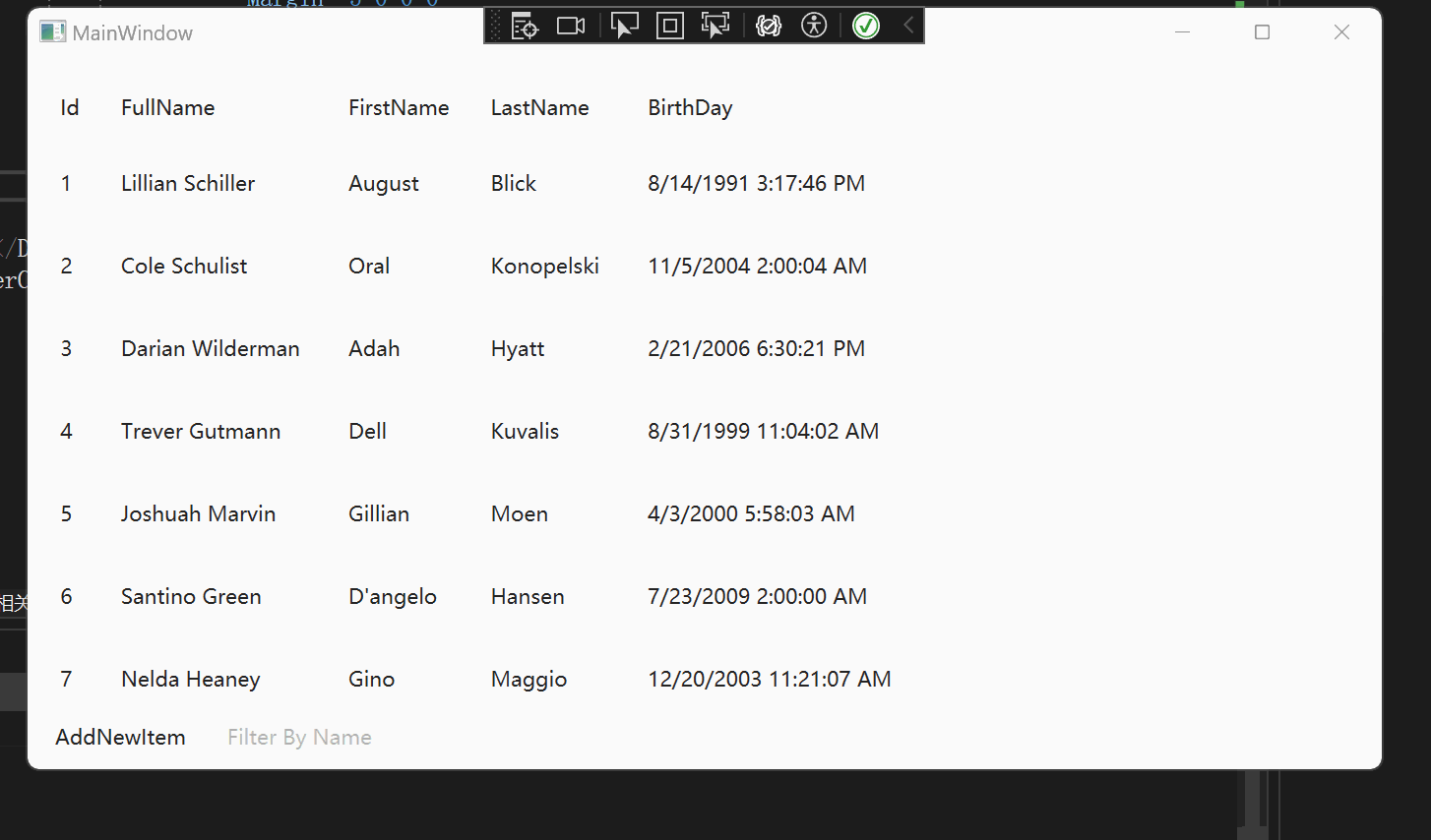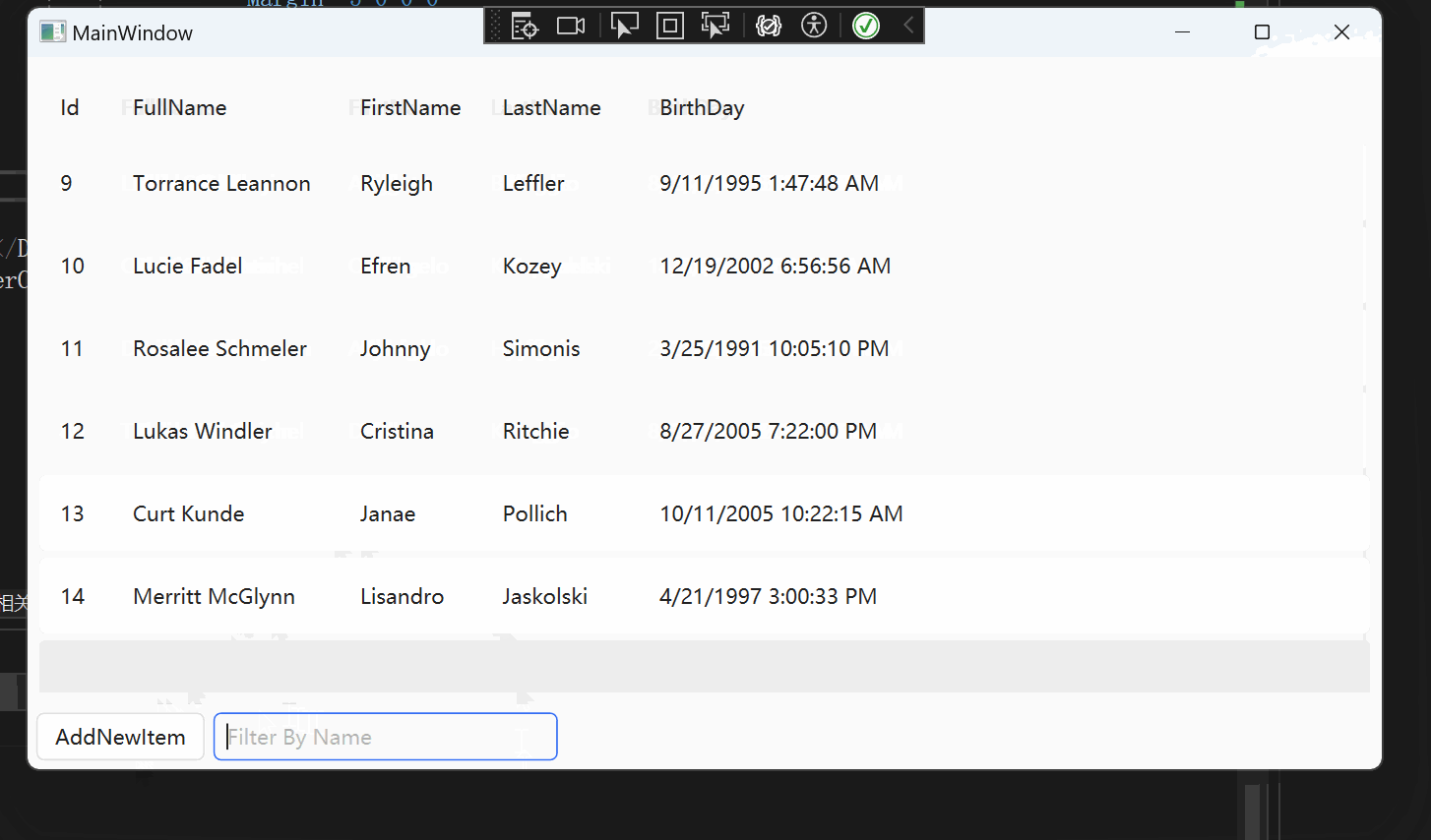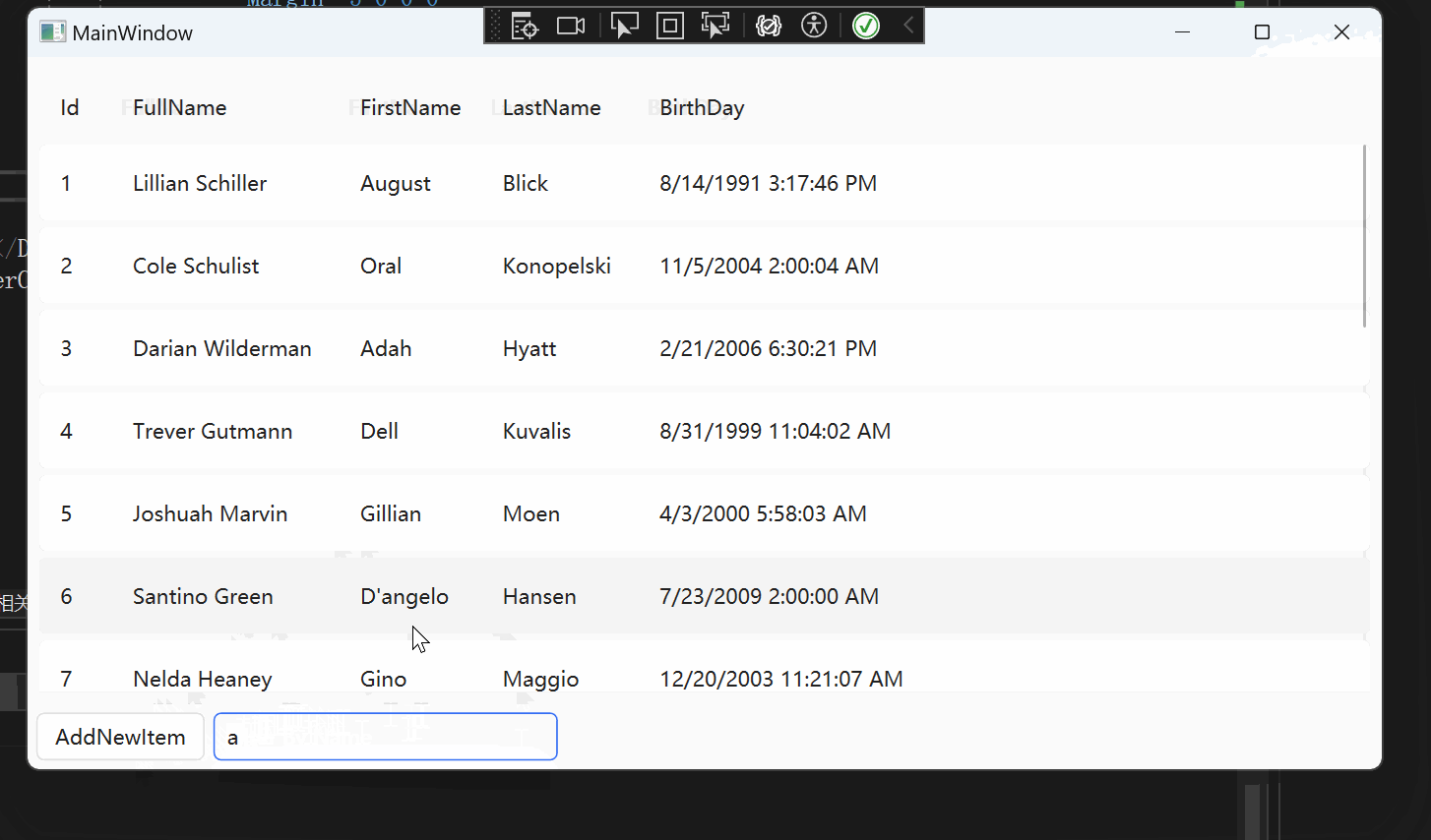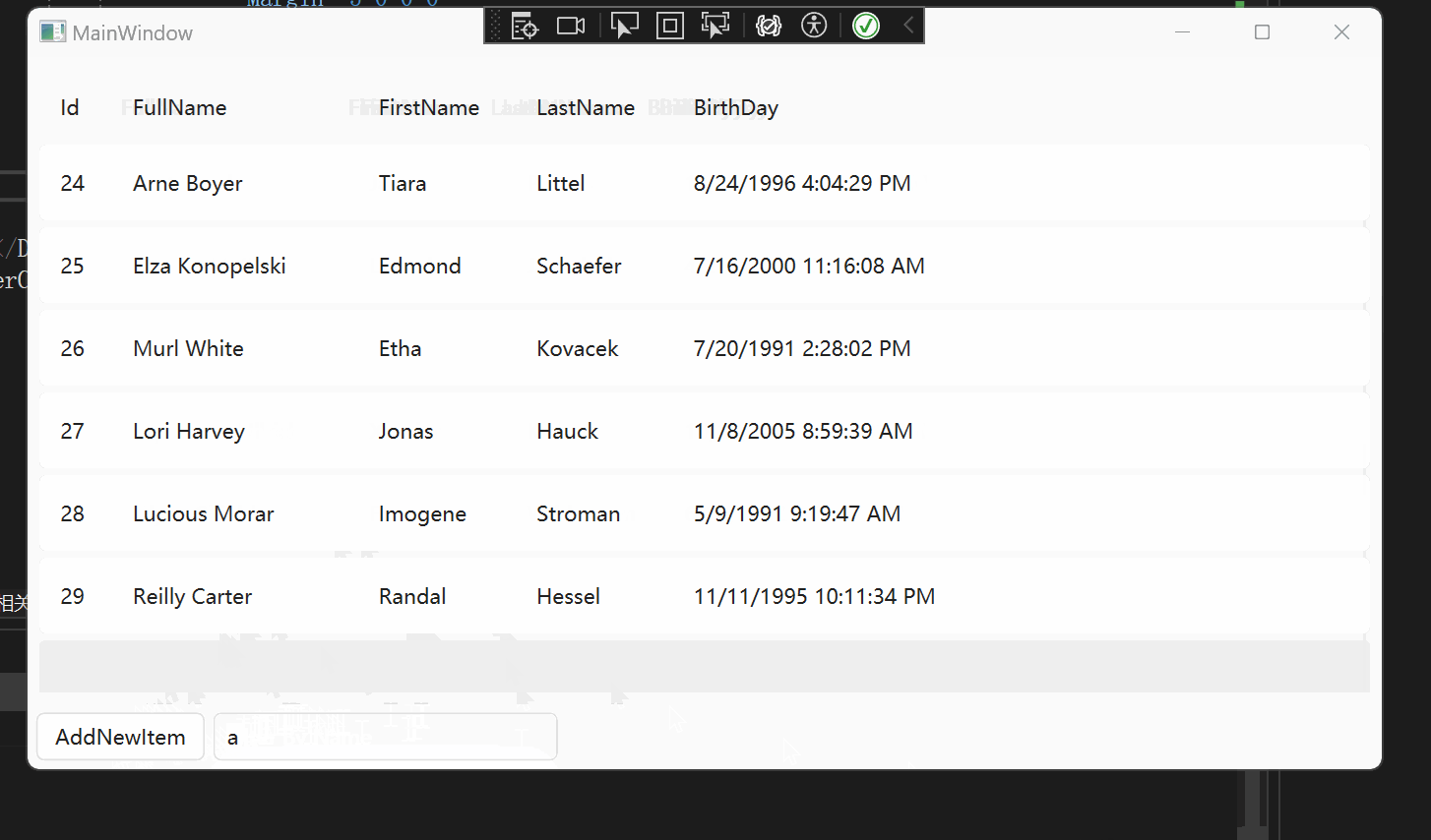
WPF 【十月的寒流】学习笔记(1):DataGrid过滤
文章目录 相关链接代码仓库前言环境DataGrid 数据筛选项目配置使用原理主要代码(详细代码可以看我的GitHub仓库)Models.PersonDataGirdViewDataGridViewModel 实现效果 DataGrid直接绑定CollectionViewxamlViewModel 总结 相关链接 十月的寒流 在 WPF 中…...

当Vue项目启动后,通过IP地址方式在相同网络段的其他电脑上无法访问前端页面?
当Vue项目启动后,通过IP地址方式在相同网络段的其他电脑上无法访问前端页面,可能是由以下几个原因造成的: 服务监听地址:默认情况下,许多开发服务器(如Vue CLI的vue-cli-service serve)只监听lo…...

native sql -ABAP开发从入门到精通笔记
Native SQL SQL概要 OPEN SQL读取数据 Select Select <lines> <columns>... Select signle <cols>.... where. 列去重数据 Select distinct <cols>... where... 当取多条数据时,select结果会保存到内表中。 Select ... into...语句的结果不…...

C++完美转发【gpt】
提问:用极其通俗易懂的文字解释C的完美转发 ChatGPT 好的,让我用非常通俗易懂的方式解释一下 C 中的完美转发。 假设你有一个房子(函数),你想把家具(参数)从一个房间(函数&#x…...

C++之类和对象(2)
目录 1.类的6个默认成员函数 2. 构造函数 2.1 概念 2.2 特性 3.析构函数 3.1 概念 3.2 特性 4. 拷贝构造函数 4.1 概念 4.2 特征 5.赋值运算符重载 5.1 运算符重载 5.2 赋值运算符重载 2. 赋值运算符只能重载成类的成员函数不能重载成全局函数 3. 用户没有显式实现时&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
