【更新完毕】2024牛客寒假算法基础集训营6 题解 | JorbanS
文章目录
- [A - 宇宙的终结](https://ac.nowcoder.com/acm/contest/67746/A)
- [B - 爱恨的纠葛](https://ac.nowcoder.com/acm/contest/67746/B)
- [C - 心绪的解剖](https://ac.nowcoder.com/acm/contest/67746/C)
- [D - 友谊的套路](https://ac.nowcoder.com/acm/contest/67746/D)
- [E - 未来的预言](https://ac.nowcoder.com/acm/contest/67746/E)
- [F - 命运的抉择](https://ac.nowcoder.com/acm/contest/67746/F)
- [G - 人生的起落](https://ac.nowcoder.com/acm/contest/67746/G)
- [I - 时空的交织](https://ac.nowcoder.com/acm/contest/67746/I)
- [J - 绝妙的平衡](https://ac.nowcoder.com/acm/contest/67746/J)
A - 宇宙的终结
暴力枚举三个数即可
int p[9] = {2, 3, 5, 7, 11, 13, 17, 19, 23};bool check(int x) {for (int i = 0; i < 9; i ++)for (int j = i + 1; j < 9; j ++)for (int k = j + 1; k < 9; k ++)if (p[i] * p[j] * p[k] == x) return true;return false;
}int solve() {int l, r; cin >> l >> r;for (int i = l; i <= r; i ++)if (check(i)) return i;return -1;
}
B - 爱恨的纠葛
找到一对数 ( a i , b j ) (a_i,~b_j) (ai, bj) 使其差最小,对于每一个 b i b_i bi,二分查找其大于等于和小于它的第一个 a i a_i ai,最后输出保证 a i a_i ai 在 b j b_j bj 所在位置
void solve() {cin >> n;map<int, int> mp;for (int i = 0; i < n; i ++) cin >> a[i];for (int i = 0; i < n; i ++) cin >> b[i];sort(a, a + n);int pos = -1, Min = 1e9, num;for (int i = 0; i < n; i ++) {int t = lower_bound(a, a + n, b[i]) - a;if (abs(b[i] - a[t]) < Min) {Min = abs(b[i] - a[t]);pos = i;num = t;}if (t && abs(b[i] - a[t - 1]) < Min) {Min = abs(b[i] - a[t - 1]);pos = i;num = t - 1;}}vector<int> c;for (int i = 0; i < n; i ++)if (i != num) c.emplace_back(a[i]);for (int i = 0; i <= pos - 1; i ++) cout << c[i] << ' ';cout << a[num] << ' ';for (int i = pos; i < n - 1; i ++) cout << c[i] << ' ';cout << endl;
}
C - 心绪的解剖
先求出 0 ∼ 1 0 9 0\sim10^9 0∼109 的斐波那契数列
法一:预处理出所有三个斐波那契数可能形成的数
int f[N];
map<int, int> p;void solve() {cin >> n;int t = p[n];if (t) {cout << a[t] << ' ' << b[t] << ' ' << c[t] << endl;} else cout << -1 << endl;
}signed main() {FastIOf[0] = 0, f[1] = 1;for (int i = 2; i <= 44; i ++) f[i] = f[i - 1] + f[i - 2];int idx = 0;for (int i = 0; i <= 44; i ++)for (int j = 0; j <= 44; j ++)for (int k = 0; k <= 44; k ++) {p[f[i] + f[j] + f[k]] = ++ idx;a[idx] = f[i];b[idx] = f[j];c[idx] = f[k];}Casessolve();return 0;
}
法二:由于每个数都可由至少另外两个数表示,所以贪心的,每次减去尽可能大的值
三次二分,每次减去二分出来的值
D - 友谊的套路
双方均有可能让二追三
void solve() {double res = 0, p; cin >> p;res += p * p * p * (1 - p) * (1 - p);res += p * p * (1 - p) * (1 - p) * (1 - p);printf("%.8lf\n", res);
}
E - 未来的预言
模拟一下
void solve() {getchar();getchar();cin >> m >> s;n = s.size();int r = 0, p = 0;for (int i = 1; i <= n; i ++) {if (s[i - 1] == 'R') r ++;else p ++;if (r > m >> 1) {cout << R << endl << i << endl;return;}if (p > m >> 1) {cout << P << endl << i << endl;return;}}cout << "to be continued." << endl << n << endl;
}
F - 命运的抉择
先预处理每个数的全部质因数( 1 1 1 特殊处理)
并查集维护每个数是否需要处于同一组
int n, m, k;
int a[N], b[N], p[N];
vector<vector<int>> e(N);int find(int x) { return x == p[x] ? x : p[x] = find(p[x]); }void solve() {cin >> n;for (int i = 1; i <= n; i ++) p[i] = i;vector<int> q;for (int i = 1; i <= n; i ++) {cin >> a[i];for (auto j : e[a[i]])if (!b[j]) b[j] = i, q.emplace_back(j);else p[find(i)] = find(b[j]);}for (auto i : q) b[i] = 0;int cnt = 0;for (int i = 2; i <= n; i ++) cnt += find(1) != find(i);if (!cnt) {cout << "-1 -1" << endl;return;}cout << n - cnt << ' ' << cnt << endl;for (int i = 1; i <= n; i ++) if (p[1] == p[i]) cout << a[i] << ' ';cout << endl;for (int i = 1; i <= n; i ++) if (p[1] != p[i]) cout << a[i] << ' ';cout << endl;
}signed main() {FastIOe[1].emplace_back(1);for (int i = 2; i <= 1e6; i ++)if (e[i].empty())for (int j = i; j <= 1e6; j += i)e[j].emplace_back(i);Casessolve();return 0;
}
G - 人生的起落
先特判当 2 k + 1 > n 2k+1\gt n 2k+1>n 时必然不成立
贪心地,让 2 1 2 2~1~2 2 1 2 作为三元组,则当 k ≠ 0 k\neq0 k=0 时若 m < n + k + 1 m\lt n+k+1 m<n+k+1 时必然不成立
若 k = 0 k=0 k=0,让除了第一个位置的所有数填 1 1 1,第一个位置填剩余的数即可
当 k > 0 k\gt0 k>0 时,
构造 x y x x~y~x x y x,使得 x x x 尽可能大,剩下的先全部放 1 1 1,设剩下的为 m , m < k + 1 m,~m\lt k+1 m, m<k+1
若正好铺满,即 2 k + 1 = n 2k+1=n 2k+1=n 时,若 x = y + 1 x=y+1 x=y+1,则不成立,否则将 m m m 个谷位置 + 1 +1 +1
若未正好铺满,则让 a [ 2 k + 1 ] : = m a[2k+1]:=m a[2k+1]:=m
void solve() {cin >> n >> m >> k;if (k * 2 + 1 > n || k && m < n + k + 1) {cout << -1 << endl;return;}for (int i = 0; i < n; i ++) a[i] = 1, m --;if (k) {for (int i = 0; i <= k << 1; i += 2) a[i] += m / (k + 1);m %= k + 1;if (k * 2 + 1 == n) {if (a[0] == a[1] + 1 && m) {cout << -1 << endl;return;}for (int i = 1; i <= m * 2 - 1; i += 2) a[i] ++;} else a[k * 2 + 1] += m;} else a[0] += m;for (int i = 0; i < n; i ++) cout << a[i] << " \n"[i == n - 1];
}
I - 时空的交织
∑ i = 1 n ∑ j = 1 m a i × b j = ∑ i = 1 n a i × ∑ j = 1 m b j \sum_{i=1}^n\sum_{j=1}^ma_i\times b_j=\sum_{i=1}^na_i\times\sum_{j=1}^m b_j ∑i=1n∑j=1mai×bj=∑i=1nai×∑j=1mbj
转化为 a , b a,~b a, b 连续子序列和的最大乘积
ll cal() {ll t = 0, A = -1e18, B = -1e18;for (int i = 0; i < n; i ++) {if (a[i] >= -t) t += a[i];else t = 0;A = max(A, t);}t = 0;for (int i = 0; i < m; i ++) {if (b[i] >= -t) t += b[i];else t = 0;B = max(B, t);}return A * B;
}ll solve() {cin >> n >> m;int MaxA = -1e9, MaxB = -1e9;int MinA = 1e9, MinB = 1e9;for (int i = 0; i < n; i ++) {cin >> a[i];MaxA = max(MaxA, a[i]);MinA = min(MinA, a[i]);}for (int i = 0; i < m; i ++) {cin >> b[i];MaxB = max(MaxB, b[i]);MinB = min(MinB, b[i]);}ll res = max(MaxA * MinB, MinA * MaxB);if (MinA >= 0 && MaxB <= 0 || MaxA <= 0 && MinB >= 0) return res;res = max(res, cal());for (int i = 0; i < n; i ++) a[i] *= -1;for (int i = 0; i < m; i ++) b[i] *= -1;res = max(res, cal());return res;
}
J - 绝妙的平衡
因为对于红节点的子树和已为 3 3 3 的倍数,则对于某一个红节点来说,无需考虑该红节点子树中的子红节点子树,将未涂色的节点和该红节点构造和为 3 3 3 的倍数即可
int n, f[N], a[N];
string s;
vector<vector<int>> e(N), E(N);
vector<int> R;void dfs(int u = 1, int fa = 0) {if (s[u] == 'W') f[u] = f[fa];for (auto v : e[u]) if (v != fa) dfs(v, u);
}void solve() {cin >> n >> s;s = " " + s;for (int i = 2; i <= n; i ++) {int x; cin >> x;e[x].emplace_back(i);}for (int i = 1; i <= n; i ++) f[i] = i, a[i] = 1;dfs();for (int i = 1; i <= n; i ++) {if (f[i] == i) R.emplace_back(i);E[f[i]].emplace_back(i);}for (auto u : R) {if (E[u].size() == 1) {cout << -1 << endl;return;}if (E[u].size() & 1) {for (int i = 0; i < 3; i ++) a[E[u][i]] = 1;for (int i = 3; i < E[u].size(); i ++) a[E[u][i]] = (i & 1) + 1;} else {for (int i = 0; i < E[u].size(); i ++) a[E[u][i]] = (i & 1) + 1;}}for (int i = 1; i <= n; i ++) cout << a[i];cout << endl;
}
相关文章:

【更新完毕】2024牛客寒假算法基础集训营6 题解 | JorbanS
文章目录 [A - 宇宙的终结](https://ac.nowcoder.com/acm/contest/67746/A)[B - 爱恨的纠葛](https://ac.nowcoder.com/acm/contest/67746/B)[C - 心绪的解剖](https://ac.nowcoder.com/acm/contest/67746/C)[D - 友谊的套路](https://ac.nowcoder.com/acm/contest/67746/D)[E …...

FL Studio All Plugins Edition2024中文完整版Win/Mac
FL Studio All Plugins Edition,常被誉为数字音频工作站(DAW)的佼佼者,是音乐制作人和声音工程师钟爱的工具。它集音频录制、编辑、混音以及MIDI制作为一体,为用户提供了从创作到最终作品输出的完整工作流程。这个版本…...

神经网络系列---归一化
文章目录 归一化批量归一化预测阶段 测试阶段γ和β(注意)举例 层归一化前向传播反向传播 归一化 批量归一化 (Batch Normalization)在训练过程中的数学公式可以概括如下: 给定一个小批量数据 B { x 1 , x 2 , … …...

2023 龙蜥操作系统大会演讲实录:《兼容龙蜥的云原生大模型数据计算系统——πDataCS》
本文主要分三部分内容:第一部分介绍拓数派公司,第二部分介绍 πDataCS 产品,最后介绍 πDataCS 与龙蜥在生态上的合作。 杭州拓数派科技发展有限公司(简称“拓数派”,英文名称“OpenPie”)是国内基础数据计…...

【Vue渗透】Vue站点渗透思路
原文地址 极核GetShell 前言 本文经验适用于前端用Webpack打包的Vue站点,阅读完本文,可以识别出Webpack打包的Vue站点,同时可以发现该Vue站点的路由。 成果而言:可能可以发现未授权访问。 识别Vue 识别出Webpack打包的Vue站…...

主数据管理是数字化转型成功的基石——江淮汽车案例分享
汽车行业数字化转型的背景 在新冠疫情导火索的影响下,经济全球化政治基础逐渐动摇。作为全球最大的汽车市场,我国的汽车市场逐渐由增量转为存量市场。 在数字化改革大背景下,随着工业4.0时代的到来,江淮汽车集团力争实现十四五数…...
----加密Encryption (CSFLE))
【Spring连载】使用Spring Data访问 MongoDB(十一)----加密Encryption (CSFLE)
[TOC](【Spring连载】使用Spring Data访问 MongoDB(十一)----加密Encryption (CSFLE)) 一级目录 二级目录 三级目录...
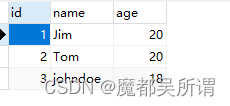
【postgresql】数据表id自增与python sqlachemy结合实例
需求: postgresql实现一个建表语句,表名:student,字段id,name,age, 要求:每次添加一个数据id会自动增加1 在PostgreSQL中,您可以使用SERIAL或BIGSERIAL数据类型来自动生成主键ID。以下是一个创建名为stude…...

什么是索引?在 MySQL 中有哪些类型的索引?它们各自的优势和劣势是什么?
什么是索引?在 MySQL 中有哪些类型的索引?它们各自的优势和劣势是什么? 索引是数据库中用于帮助快速查询数据的一种数据结构。在 MySQL 中,索引可以显著提高查询性能,因为它允许数据库系统不必扫描整个表来找到相关数据…...

Docker安装与基础知识
目录 -----------------Docker 概述--------------------------- 容器化越来越受欢迎,因为容器是: Docker与虚拟机的区别: Docker核心概念: ●镜像 ●容器 ●仓库 -----------------安装 Docker--------------------------…...
搭建Facebook直播网络对IP有要求吗?
在当今数字化时代,Facebook直播已经成为了一种极具吸引力的社交形式,为个人和企业提供了与观众直接互动的机会,成为推广产品、分享经验、建立品牌形象的重要途径。然而,对于许多人来说,搭建一个稳定、高质量的Facebook…...
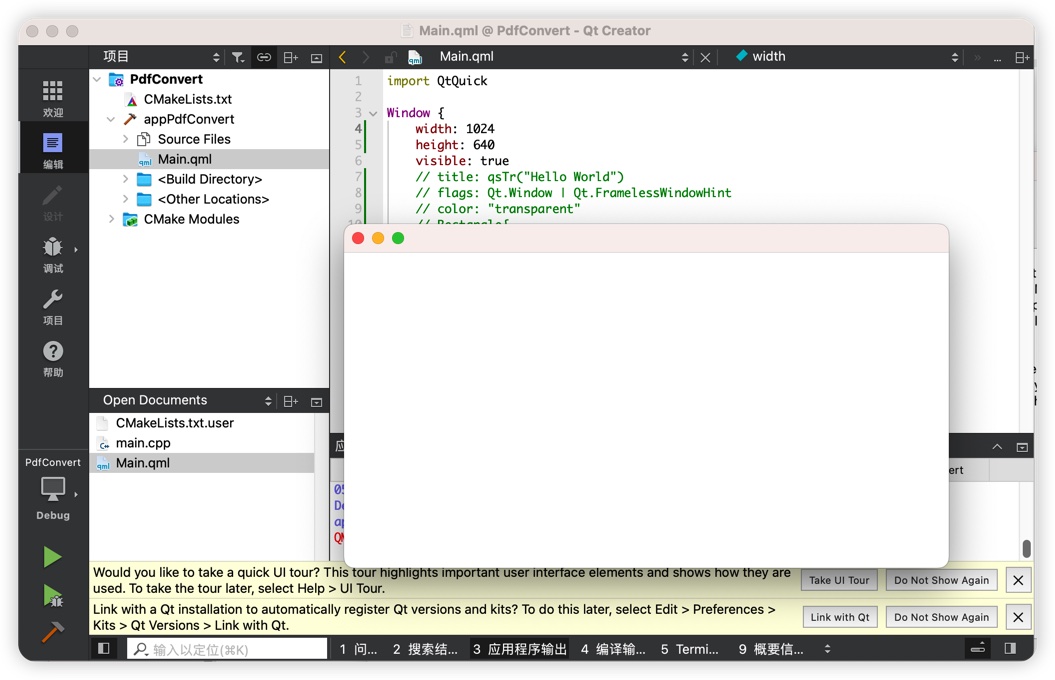
Qt开发:MAC安装qt、qtcreate(配置桌面应用开发环境)
安装qt-creator brew install qt-creator安装qt brew install qt查看qt安装路径 brew info qtzhbbindembp ~ % brew info qt > qt: stable 6.6.1 (bottled), HEAD Cross-platform application and UI framework https://www.qt.io/ /opt/homebrew/Cellar/qt/6…...

python学习网站
Python系列干货之——Python与设计模式 - 知乎 Python之23种设计模式_23种设计模式 python-CSDN博客 用python实现设计模式 — python-golang-web-guide 0.1 文档 python设计模式_Python六大原则,23种设计模式 - 掘金 Python 常用设计模式 Python入门 类class提…...

编程笔记 Golang基础 033 反射的类型与种类
编程笔记 Golang基础 033 反射的类型与种类 一、反射的类型和种类二、切片与反射三、集合与反射四、结构体与反射五、指针与反射六、函数与反射小结 反射机制的作用范围涵盖了几乎所有的类型和值的操作层面,它极大地增强了Go语言在运行时对于自身类型系统的探索和操…...
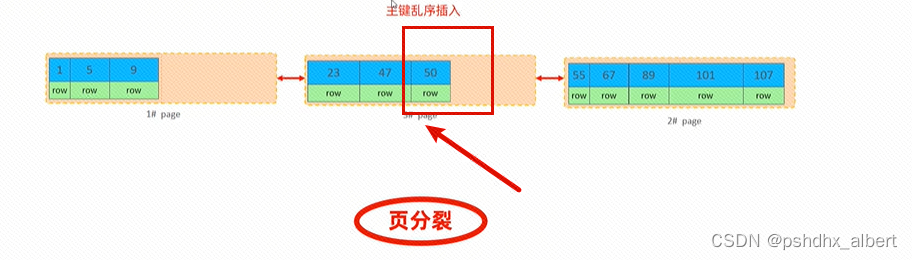
MySQL进阶篇2-索引的创建和使用以及SQL的性能优化
索引 mkdir mysql tar -xvf mysqlxxxxx.tar -c myql cd mysql rpm -ivh .....rpm yum install openssl-devel systemctl start mysqld gerp temporary password /var/log/mysqld.log mysql -u root -p mysql> show variables like validate_password.% set glob…...

基于SVM的功率分类,基于支持向量机SVM的功率分类识别,Libsvm工具箱详解
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 完整代码和数据下载链接:基于SVM的功率分类,基于支持向量机SVM的功率分类识别资源-CSDN文库 https://download.csdn.net/download/abc991835105/88862836 SVM应用实例, 基于…...
【IO流】FileWrite字符输出流
FileWrite字符输出流 1. 概述2. 作用3. 方法4. 细节5. 代码示例6. 注意事项 1. 概述 java.io.FileWriter 类是写出字符到文件的便利类。构造时使用系统默认的字符编码和默认字节缓冲区。 FileWriter 是用于写入字符数据到文件的字符输出流。 2. 作用 写入字符数据:…...
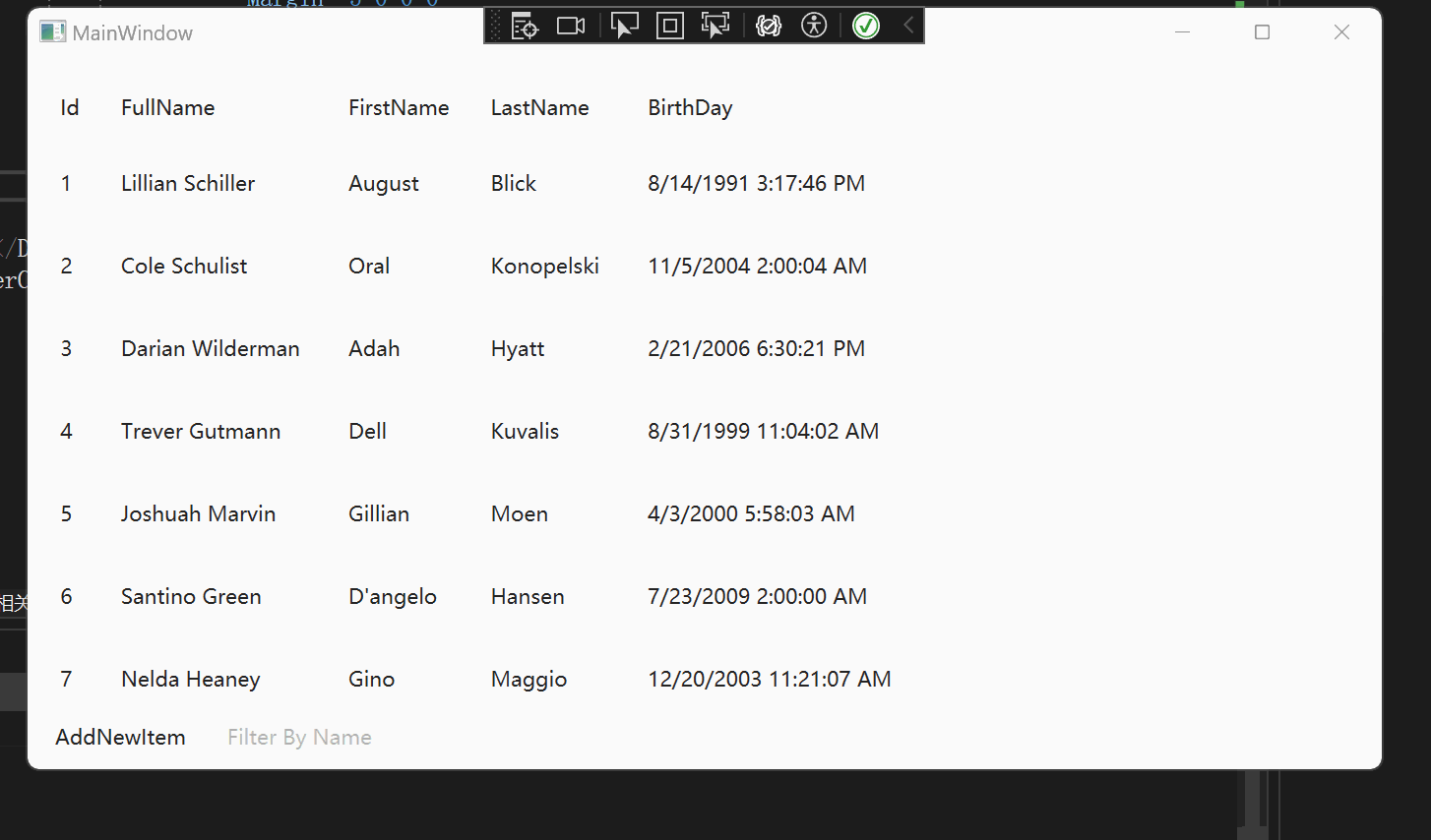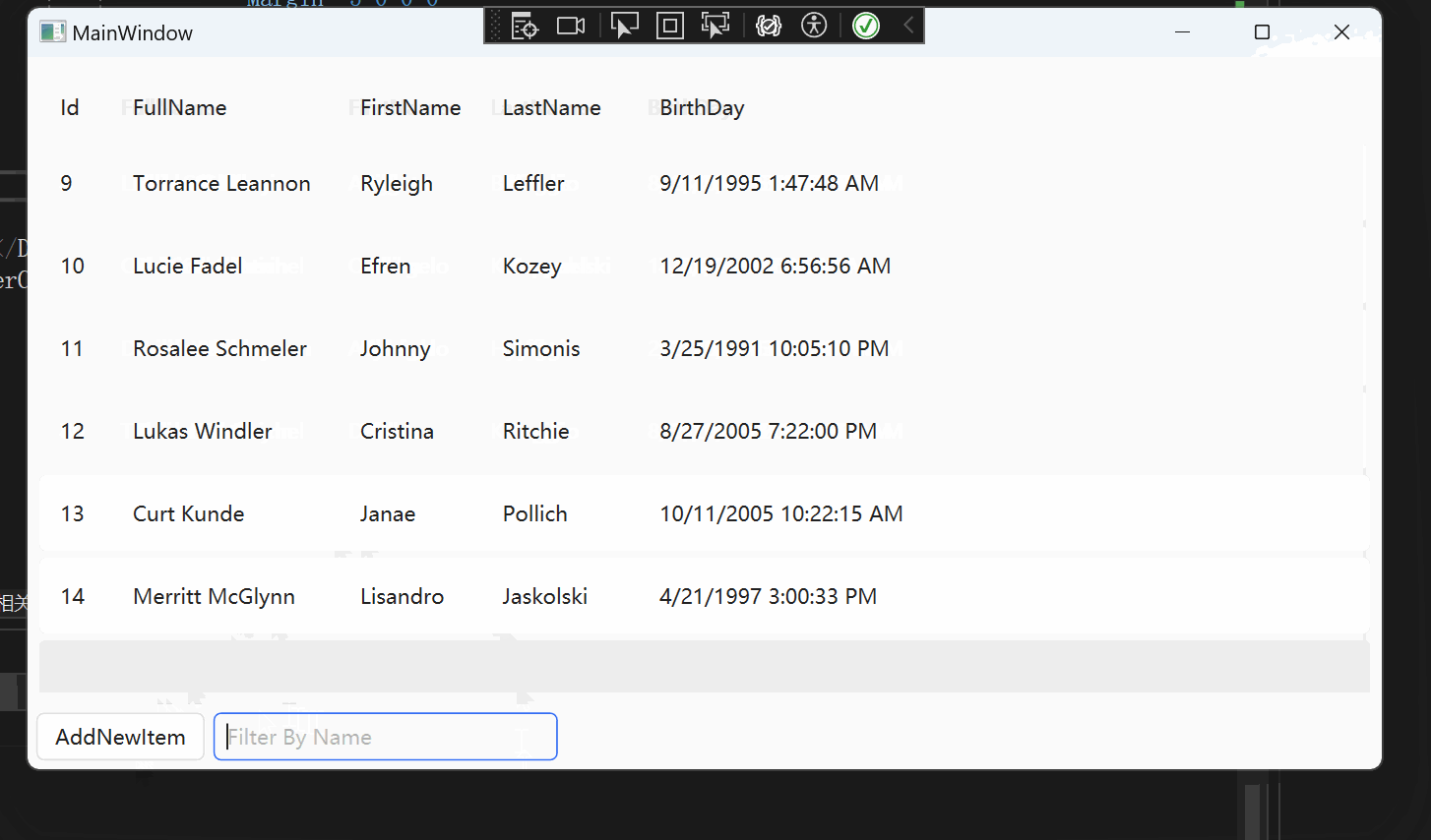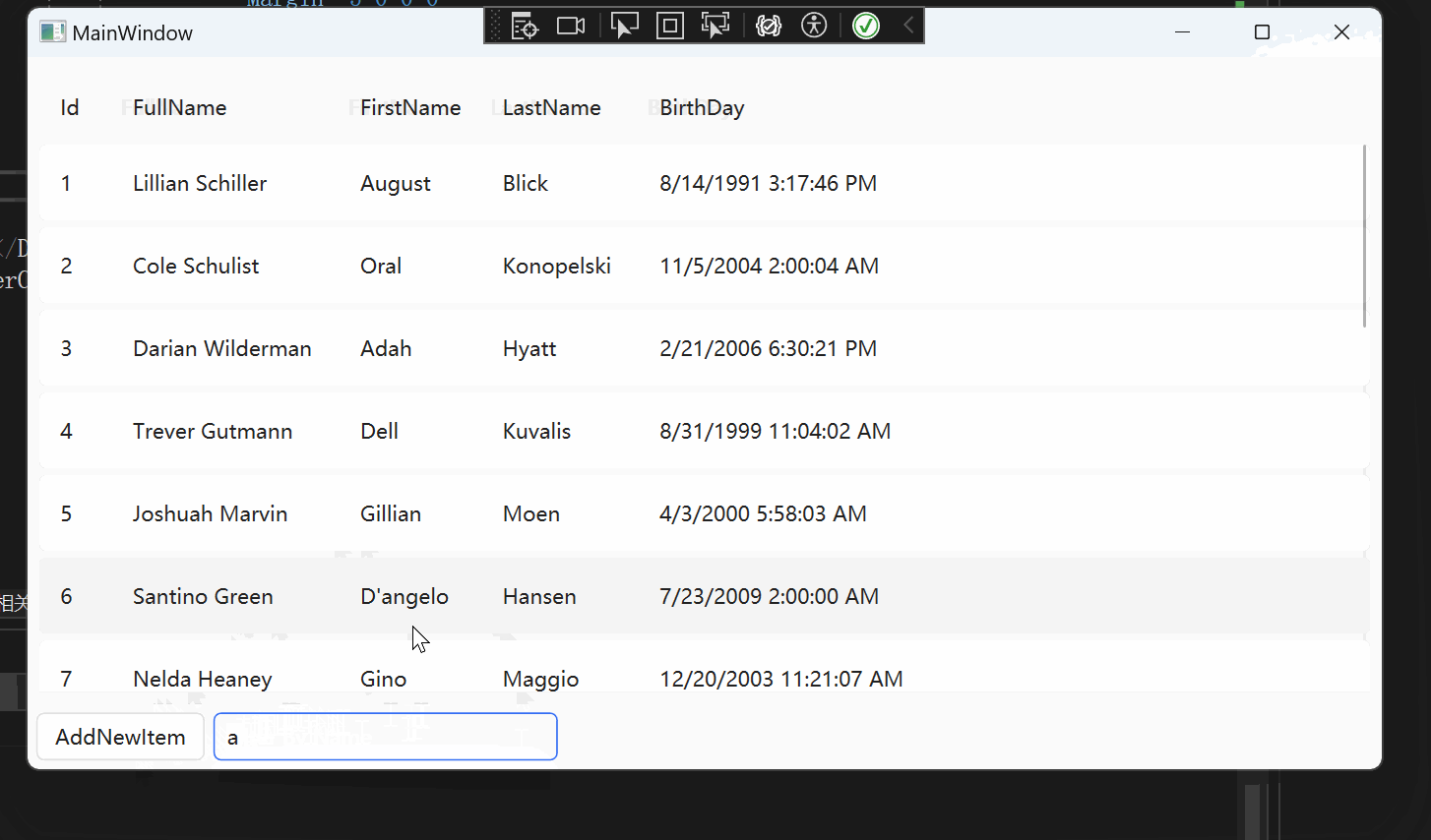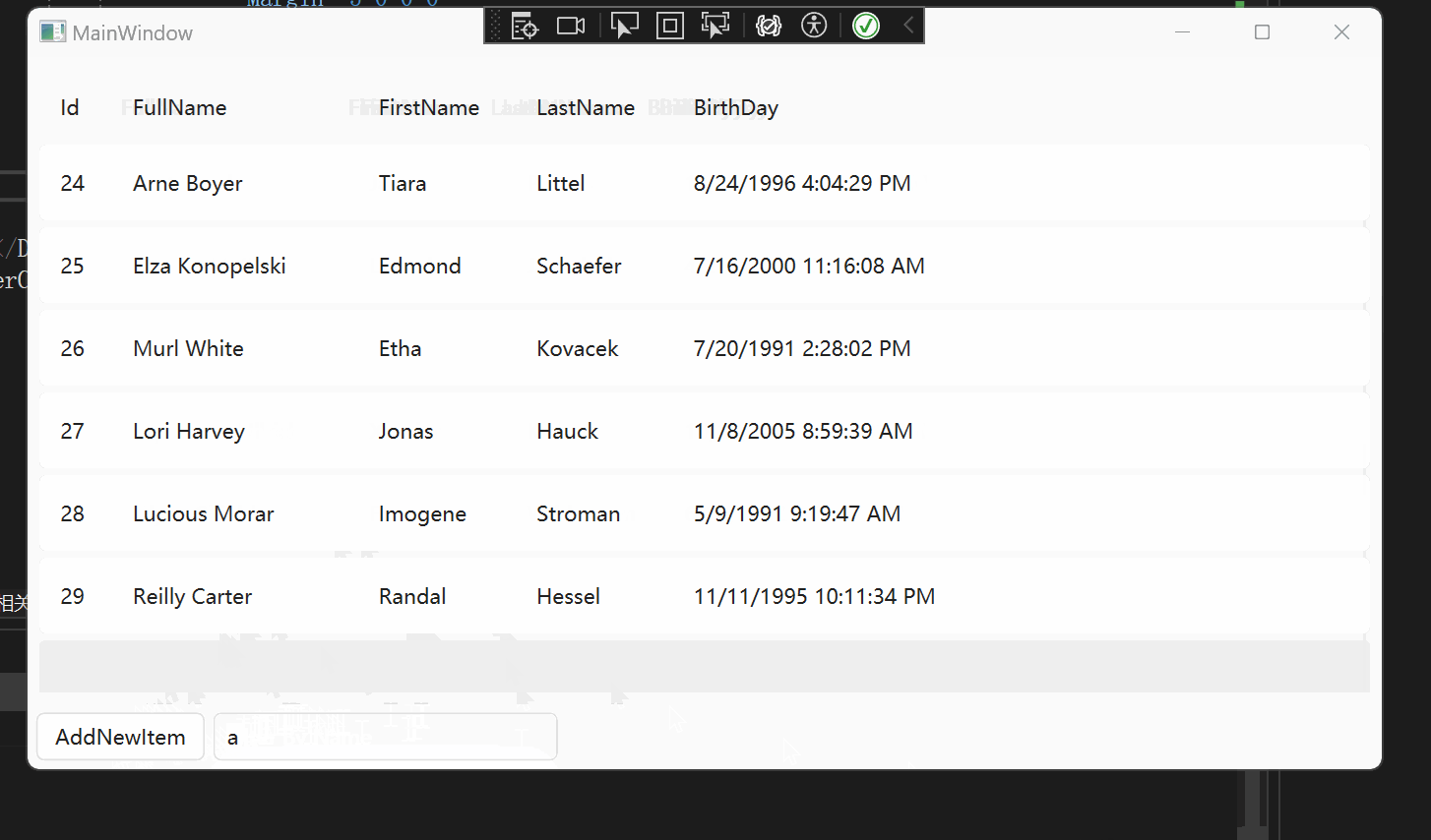
WPF 【十月的寒流】学习笔记(1):DataGrid过滤
文章目录 相关链接代码仓库前言环境DataGrid 数据筛选项目配置使用原理主要代码(详细代码可以看我的GitHub仓库)Models.PersonDataGirdViewDataGridViewModel 实现效果 DataGrid直接绑定CollectionViewxamlViewModel 总结 相关链接 十月的寒流 在 WPF 中…...

当Vue项目启动后,通过IP地址方式在相同网络段的其他电脑上无法访问前端页面?
当Vue项目启动后,通过IP地址方式在相同网络段的其他电脑上无法访问前端页面,可能是由以下几个原因造成的: 服务监听地址:默认情况下,许多开发服务器(如Vue CLI的vue-cli-service serve)只监听lo…...

native sql -ABAP开发从入门到精通笔记
Native SQL SQL概要 OPEN SQL读取数据 Select Select <lines> <columns>... Select signle <cols>.... where. 列去重数据 Select distinct <cols>... where... 当取多条数据时,select结果会保存到内表中。 Select ... into...语句的结果不…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
