Leetcoder Day26| 回溯part06:总结+三道hard题
332.重新安排行程
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。
提示:
- 如果存在多种有效的行程,请你按字符自然排序返回最小的行程组合。例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前
- 所有的机场都用三个大写字母表示(机场代码)。
- 假定所有机票至少存在一种合理的行程。
- 所有的机票必须都用一次 且 只能用一次。
示例 1:
- 输入:[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
- 输出:["JFK", "MUC", "LHR", "SFO", "SJC"]
示例 2:
- 输入:[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
- 输出:["JFK","ATL","JFK","SFO","ATL","SFO"]
- 解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。
这道题目有几个难点:
- 一个行程中,如果航班处理不好容易变成一个圈,成为死循环
- 有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
- 使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
- 搜索的过程中,如何遍历一个机场所对应的所有机场。
下面是一个有重复机场的例子 出发机场和到达机场也会重复的,如果在解题的过程中没有对集合元素处理好,就会死循环。
出发机场和到达机场也会重复的,如果在解题的过程中没有对集合元素处理好,就会死循环。
对于记录映射关系,可以用哈希集合。在这个过程中,需要可以增删元素。因为出发机场和到达机场是会重复的,搜索的过程没及时删除目的机场就会死循环。

按照回溯三部曲:
- 递归函数参数:要有机票数ticketNum,还要判断机票是否使用过,所以加一个bool数组used,注意,这里函数的返回值用的是bool,因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线。之前在二叉树部分有总结过:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值。
- 递归终止条件:本题的终止条件可以这样考虑,如[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]],有四张机票,5个机场,那么行程里的机场个数是5就可以了,也就是path里机场个数等于ticketNum+1
- 单层搜索的逻辑:如果这张机票没有被使用过,且当前机票的第一个机场,等于path里的最后一个机场,就可以将其添加进path。
class Solution {LinkedList<String> res;LinkedList<String> path=new LinkedList<>();public boolean backTracking(List<List<String>> tickets, boolean[] used){if(path.size()==tickets.size()+1){res=new LinkedList(path);return true;}for(int i=0;i<tickets.size();i++){if(!used[i] && tickets.get(i).get(0).equals(path.getLast())){used[i]=true;path.add(tickets.get(i).get(1));if(backTracking(tickets, used)){return true;}used[i]=false;path.removeLast();}}return false;}public List<String> findItinerary(List<List<String>> tickets) {Collections.sort(tickets, (a,b)->a.get(1).compareTo(b.get(1)));boolean[] used=new boolean[tickets.size()];path.add("JFK");backTracking(tickets, used);return res;}
}现在leetcode里这个方法已经超时了。
51. N皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
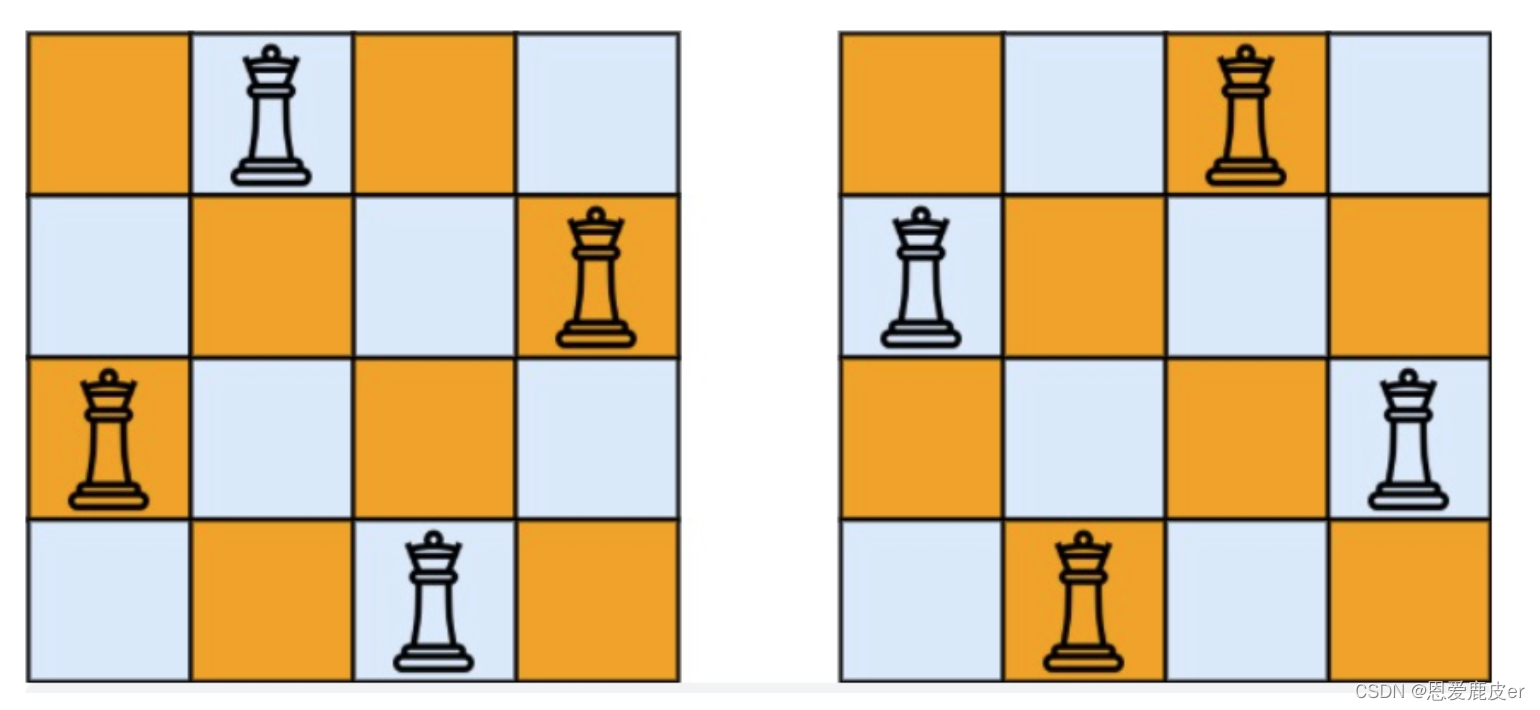
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如图所示,4 皇后问题存在两个不同的解法。
n皇后问题是回溯算法解决的经典问题,首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
下面用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:

从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
- 递归函数参数:依然定义全局变量二维数组result来记录最终结果。参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层。
- 终止条件:递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回
- 单层搜索的逻辑:递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。每次都是要从新的一行的起始位置开始搜,所以都是从0开始。这里面还涉及验证当前位置是否合法的方法,需要按照约束条件进行去重。这里不需要检查行是否重复,因为在单层搜索的过程中,每一层递归,只会选同一行里的一个元素,所以不用去重了。
在N皇后问题中,我们通常只考虑两个对角线方向:从左上角到右下角的45度对角线和从右上角到左下角的135度对角线。
这里还要注意⚠️,在将当前度棋盘结果添加到res中时,要将chessboard转换为List:res.add(Array2List(chessboard)); 因为原先的chessboard为二维数组:
public List Array2List(char[][] chessboard) {List<String> list = new ArrayList<>();for (char[] c : chessboard) {list.add(String.copyValueOf(c));}return list;}class Solution {List<List<String>> res =new ArrayList<>();public List ArraytoList(char[][] chessboard){List<String> list = new ArrayList<>();for(char[] c:chessboard){list.add(String.copyValueOf(c));}return list;}public boolean isValid(int row, int col, int n, char[][] chessboard){//检查列for(int i=0;i<row;i++){if(chessboard[i][col]=='Q'){return false;}}//检查45度斜线for(int i=row-1, j=col-1;i>=0 && j>=0; i--, j--){if(chessboard[i][j]=='Q'){return false;}}//检查135度斜线for(int i=row-1, j=col+1; i>=0 && j<n;i--,j++){if(chessboard[i][j]=='Q'){return false;}}return true;}public void backTracking(int n, int row, char[][] chessboard){if(row==n){res.add(ArraytoList(chessboard));return;}for(int col=0;col<n;col++){if(isValid(row, col, n, chessboard)){chessboard[row][col]='Q';backTracking(n, row+1, chessboard);chessboard[row][col]='.';}}}public List<List<String>> solveNQueens(int n) {char[][] chessboard=new char[n][n];for(char[]c:chessboard){Arrays.fill(c,'.');}backTracking(n,0,chessboard);return res;}
}总结
回溯部分涉及到的题型比较多,而且在二叉树环节也用到了回溯。回溯的问题都可以抽象为树结构,并且其本质是递归,也就是,只要有递归就会有回溯!这次刷题从代码随想录里学到了很有用的回溯模板,但是也不能只依赖于套模板,要具体问题具体分析。
回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
回溯的模板:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}组合问题
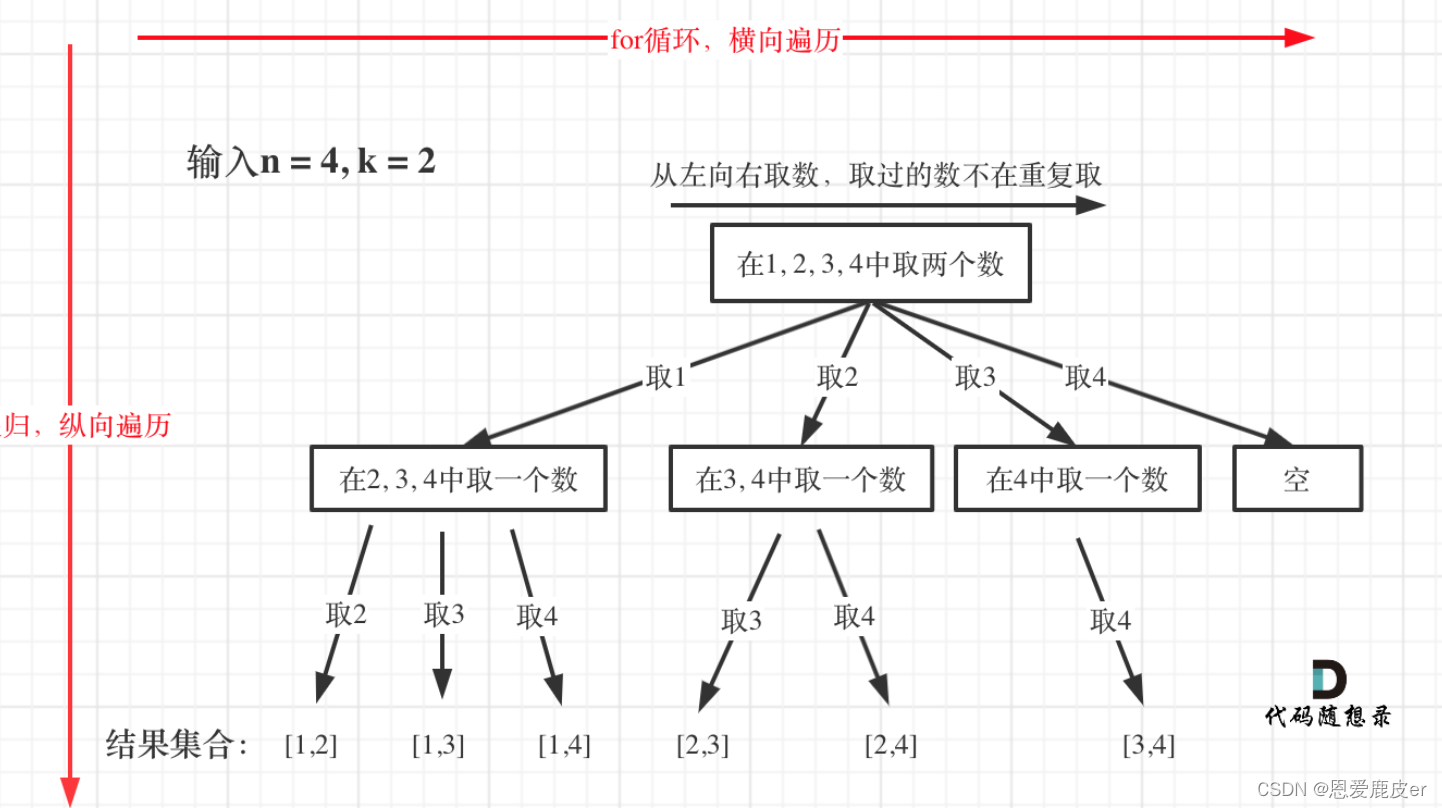
for循环横向遍历,递归纵向遍历,回溯不断调整结果集,因为取过的元素不再重复取,所以需要startIdx。如果是一个集合来求组合的话,就需要startIndex,如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,比如电话号码组合问题。
优化回溯算法只有剪枝一种方法,思路就是如果剩下的元素个数已经不满足需要的元素,就停止搜索。
(1)如果有元素总和的限制,剪枝的思路就是已选元素总和如果已经大于n(题中要求的和)了,那么往后遍历就没有意义了,直接剪掉
(2)如果包含重复数值的元素,那么使用过的就不能再次使用,carl哥用树枝重复和树层重复来进行细分。可以通过创建一个used数组来记录,也可以使用startIdx来进行去重,先对数组进行排序,如果candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
(3)多个集合来求组合,就不需要startIdx,而是从0开始遍历。
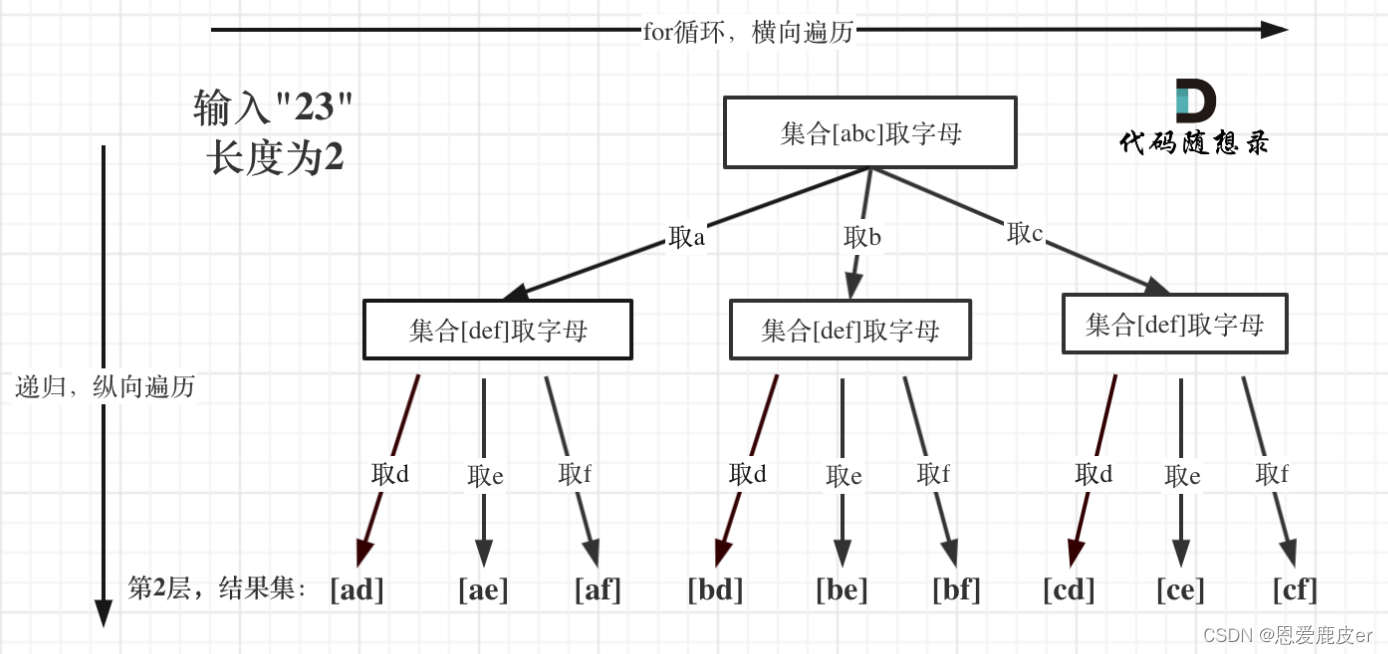
切割问题
切割问题有如下几个难点:
- 切割问题其实类似组合问题
- 如何模拟那些切割线
- 切割问题中递归如何终止
- 在递归循环中如何截取子串
- 如何判断回文
如果想到了用求解组合问题的思路来解决 切割问题本题就成功一大半了,接下来就可以对着模板照葫芦画瓢。但后序如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了。
所以本题应该是一个道hard题目了。除了这些难点,本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1。
树形结构如下:
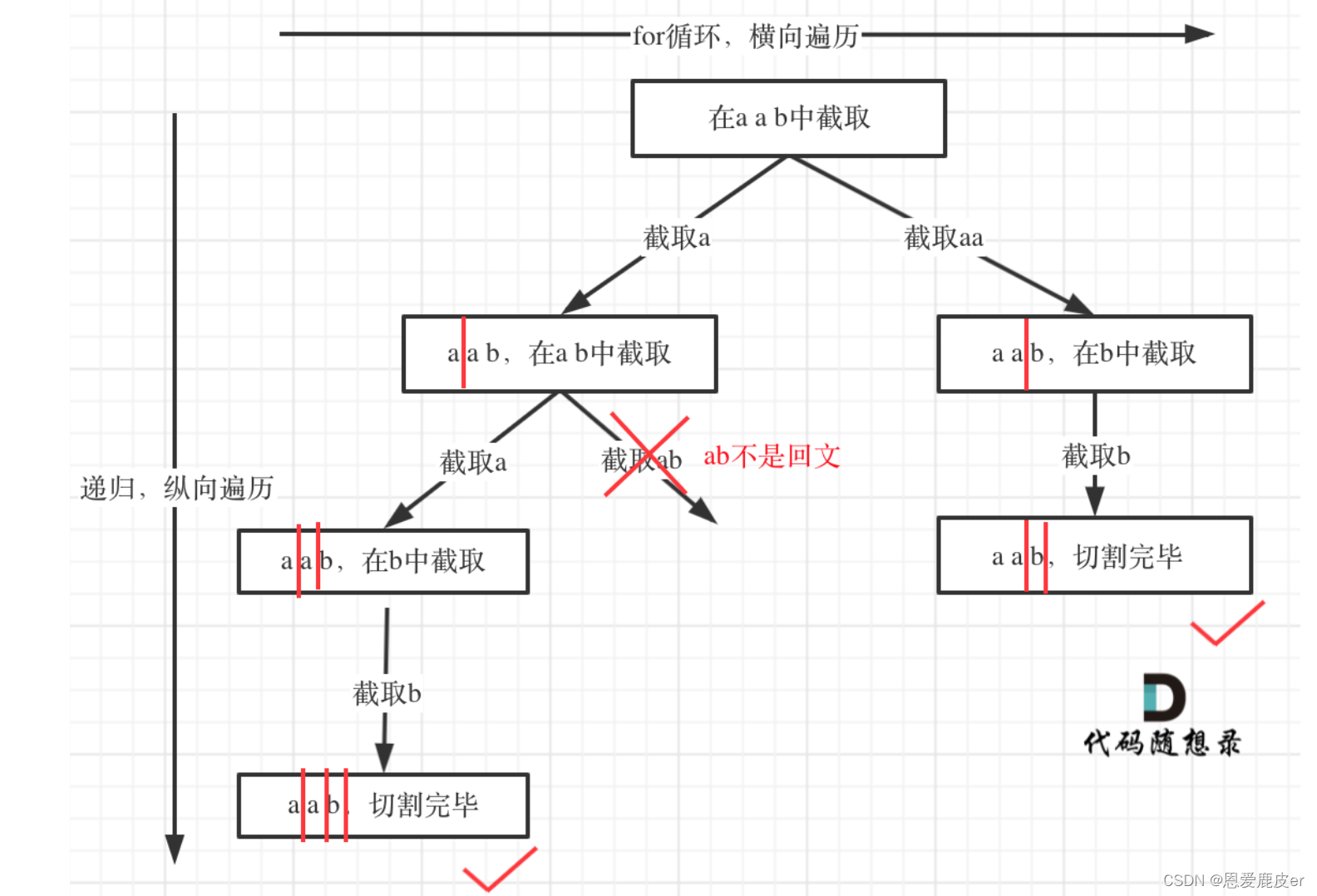
子集问题
要记住,在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
子集问题一般都会先进行排序,注意:result.push_back(path);要放在终止条件的上面,如下:
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉结果
if (startIndex >= nums.size()) { // 终止条件可以不加return;
}在求递增子序列的时候一定注意,不可以进行排序。所以可以借助哈希集合,记录当前元素是否被使用过。
排列问题
排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素
相关文章:

Leetcoder Day26| 回溯part06:总结+三道hard题
332.重新安排行程 给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必…...
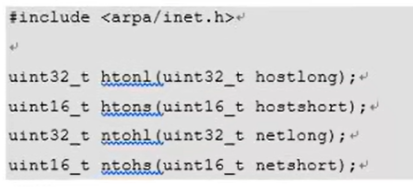
浅谈 Linux 网络编程 - 网络字节序
文章目录 前言核心知识关于 小端法关于 大端法网络字节序的转换 函数 前言 在进行 socket 网络编程时,会用到字节流的转换函数、例如 inet_pton、htons 等,那么为什么要用到这些函数呢,本篇主要就是对这部分进行介绍。 核心知识 重点需要记…...
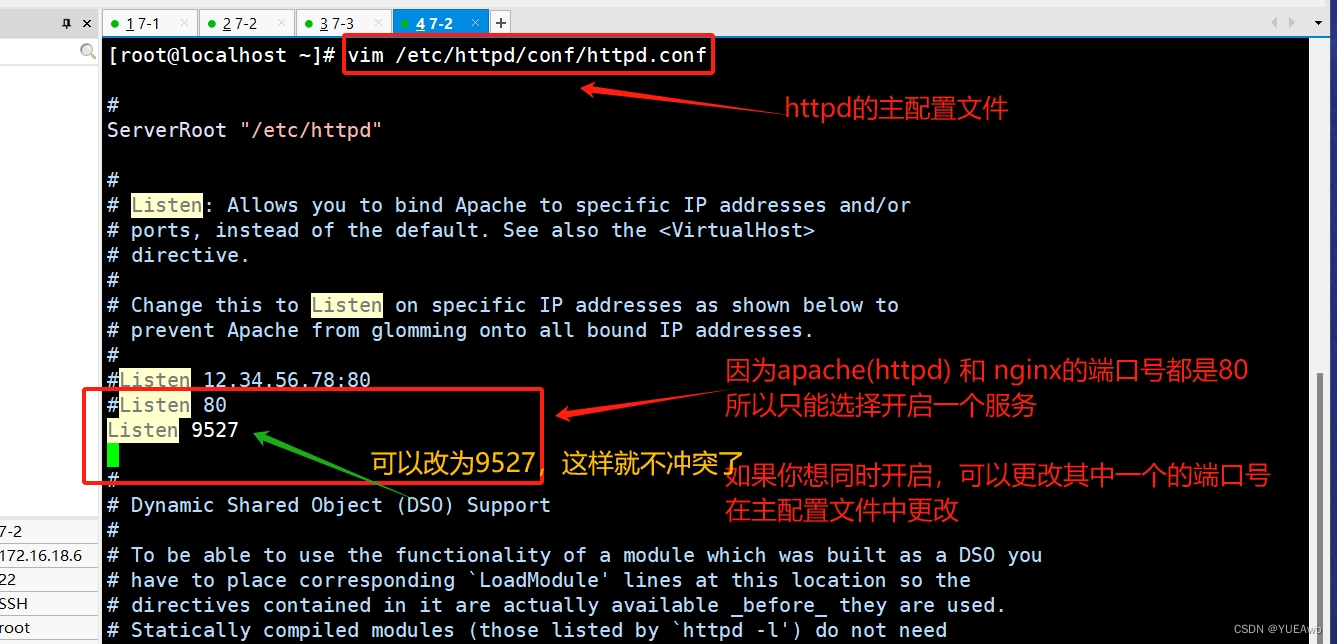
Nginx网络服务六-----IP透传、调度算法和负载均衡
1.实现反向代理客户端 IP 透传 就是在日志里面加上一个变量 Module ngx_http_proxy_module [rootcentos8 ~]# cat /apps/nginx/conf/conf.d/pc.conf server { listen 80; server_name www.kgc.org; location / { index index.html index.php; root /data/nginx/html/p…...
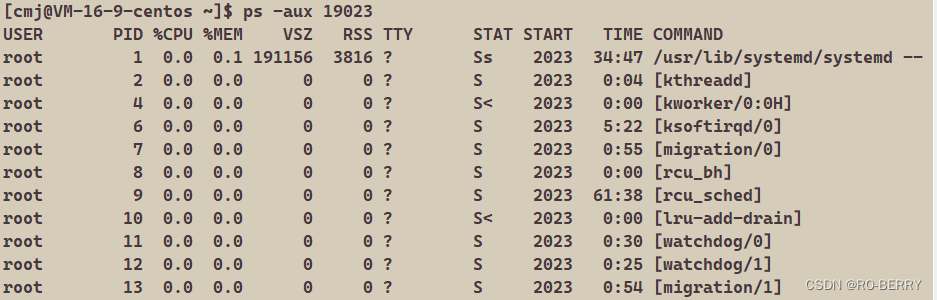
【Linux进程】进程状态---进程僵尸与孤儿
📙 作者简介 :RO-BERRY 📗 学习方向:致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 📒 日后方向 : 偏向于CPP开发以及大数据方向,欢迎各位关注,谢谢各位的支持 目录 1.进程排队2.进程状态…...
一)
MySQL数据库基础知识总结(适合小白入门使用)一
文章目录 一 数据库数据表的创建等基本操作二 数据类型的测试三 完整性约束条件四 数据表结构的相关操作五 对表中数据的操作六 表达式与查询七 高级的查询功能 一 数据库数据表的创建等基本操作 #注释内容(与python很像) -- 也为注释内容 -- 创建一个数…...

历史新知网:寄快递寄个电脑显示器要多少钱?
以下文字信息由(新史知识网)编辑整理发布。 让我们赶紧来看看吧! 问题1:快递寄电脑显示器要多少钱? 此物有多重? 顺丰寄就可以了,但是必须是原包装的,不然不好寄。 问题2࿱…...

在两台CentOS 7服务器上部署MinIO集群。
环境说明: 2台Centos7服务器 IP地址分别为172.16.1.9和172.16.1.10 1. 创建minio用户和目录 在两台服务器上执行以下命令: sudo useradd -m -d /app/minio minio sudo mkdir -p /app/minioData sudo mkdir -p /app/minio/logs sudo chown -R mini…...

【计算机网络】深度学习使用应用层的HTTP协议
💓 博客主页:从零开始的-CodeNinja之路 ⏩ 收录文章:【计算机网络】深度学习使用应用层的HTTP协议 🎉欢迎大家点赞👍评论📝收藏⭐文章 文章目录 一:HTTP是什么二:HTTP请求1.HTTP请求的组成2.HTTP请求的方法…...
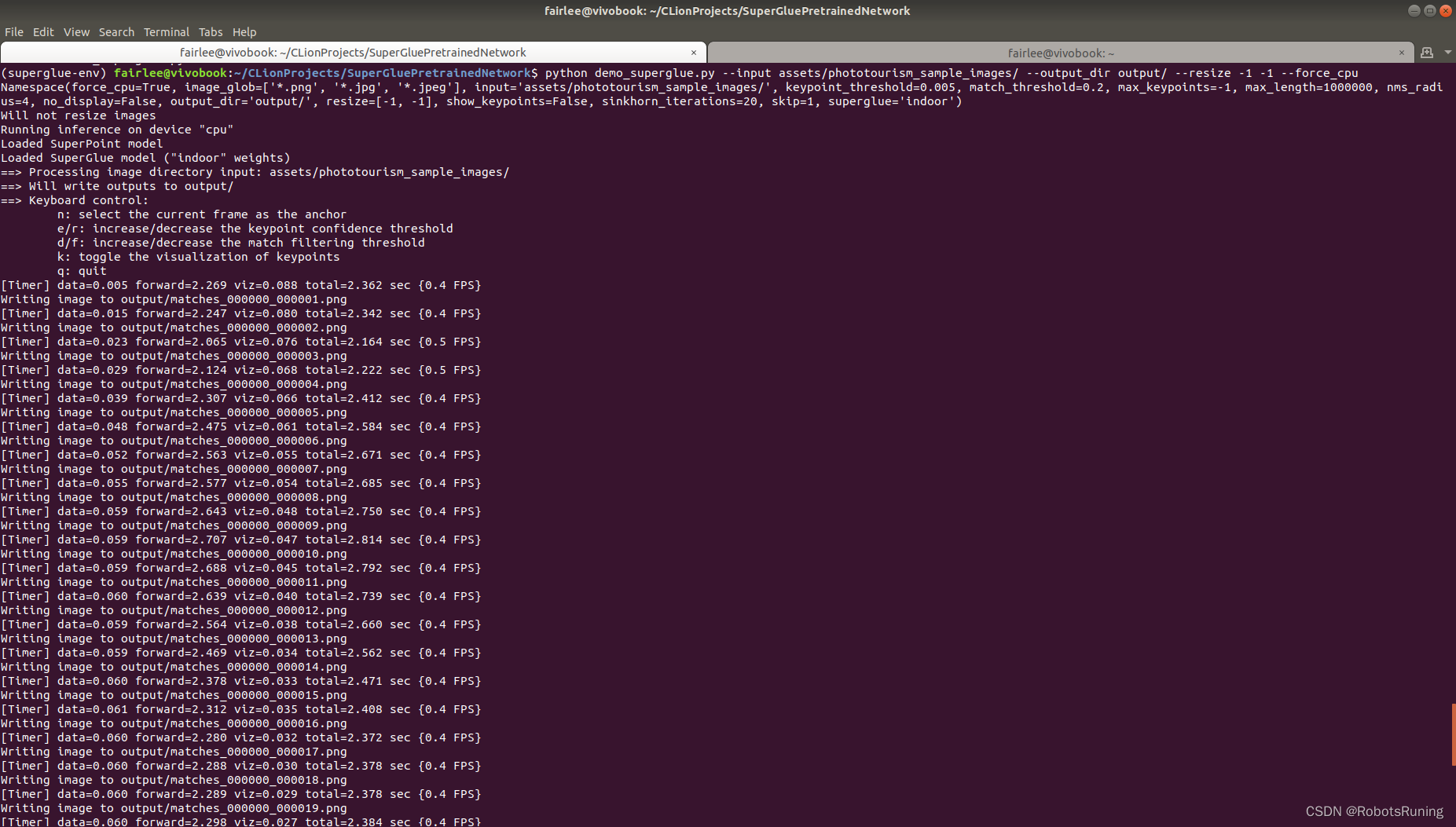
Ubuntu18.04 系统上配置并运行SuperGluePretrainedNetwork(仅使用CPU)
SuperGlue是Magic Leap在CVPR 2020上展示的研究项目,它是一个图神经网络(Graph Neural Network)和最优匹配层(Optimal Matching layer)的结合,训练用于对两组稀疏图像特征进行匹配。这个项目提供了PyTorch代…...
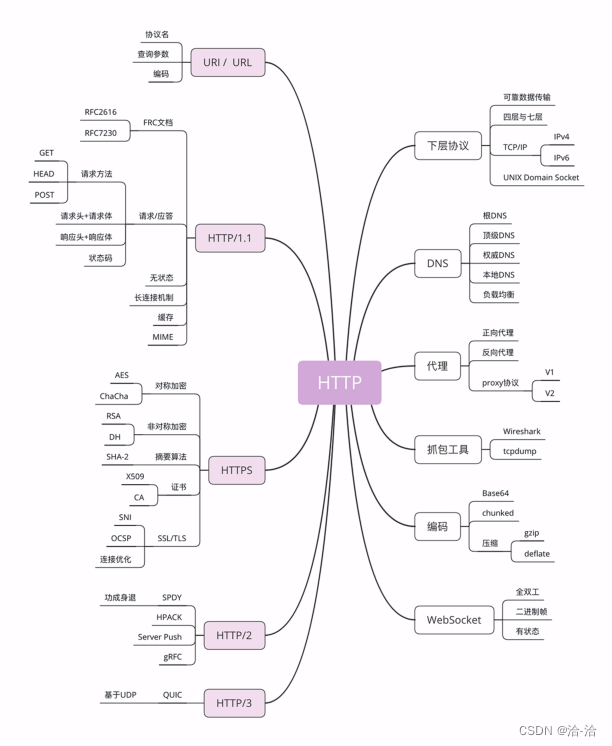
协议-http协议-基础概念01-发展历程-http组成-http是什么-相关的应用-相关的协议
发展历程-http组成-http是什么-相关的应用-相关的协议 参考来源: 极客时间-透视HTTP协议(作者:罗剑锋); 01-HTTP的发展历程 1989 年,任职于欧洲核子研究中心(CERN)的蒂姆伯纳斯 - 李(Tim Ber…...

UI学习-学习内容
教程网址1:UI 新手如何从设计规范中提升自己 推荐一下高质量的设计规范 满屏干货 语雀 B站地址1:新像素 UI 新手如何从设计规范中提升自己 推荐一下高质量的设计规范 满屏干货 UI设计培训_哔哩哔哩_bilibili 教程地址2:UI 新手成长经验分享…...

Flink CDC 提取记录变更时间作为事件时间和 Hudi 表的 precombine.field 以及1970-01-01 取值问题
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

【网络安全】网络安全意识教育实用指南
随着科技的不断发展和数字世界的变革,我们不仅从中获得前所未有的力量,也同时面临着前所未有的风险挑战。多数CISO(首席信息安全官)时刻致力于协助企业抵御各种安全威胁。在“武器库”中有一件珍贵的法宝:网络安全意识…...

wordpress模板购买网站推荐
简站wordpress主题 老牌wordpress开发团队,开发过数百款wordpress主题,作品是最好的简历,靠作品说话,看作品喜欢不喜欢就可以了。 https://www.jianzhanpress.com WP模板牛 免费wordpress下载网站,上面有上百款免费…...

LeetCode 刷题 [C++] 第240题.搜索二维矩阵 II
题目描述 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。 每列的元素从上到下升序排列。 题目分析 通过分析矩阵的特点发现,其左下角和右上角可以看作一个“二叉搜索树的根节…...
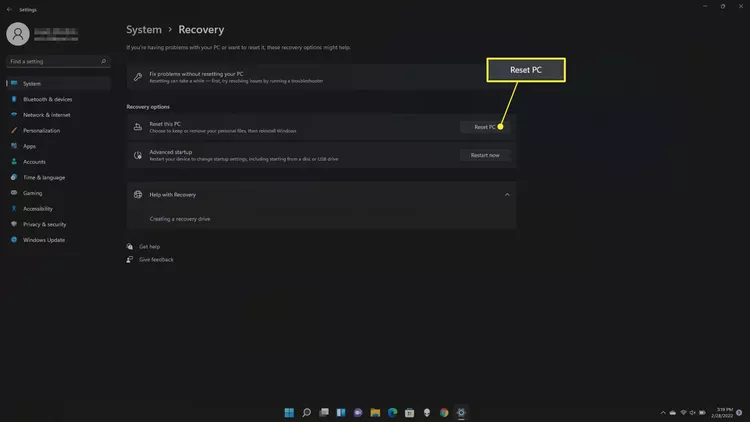
HP笔记本电脑如何恢复出厂设置?这里提供几种方法
要恢复出厂设置Windows 11或10的HP笔记本电脑,你可以使用操作系统的标准方法。如果你运行的是早期版本,你可以使用HP提供的单独程序清除计算机并重新安装操作系统。 恢复出厂设置运行Windows 11的HP笔记本电脑 所有Windows 11计算机都有一个名为“重置此电脑”的功能,可…...
Elasticsearch:了解人工智能搜索算法
作者:来自 Elastic Jessica Taylor, Aditya Tripathi 人工智能工具无处不在,其原因并不神秘。 他们可以执行各种各样的任务并找到许多日常问题的解决方案。 但这些应用程序的好坏取决于它们的人工智能搜索算法。 简单来说,人工智能搜索算法是…...
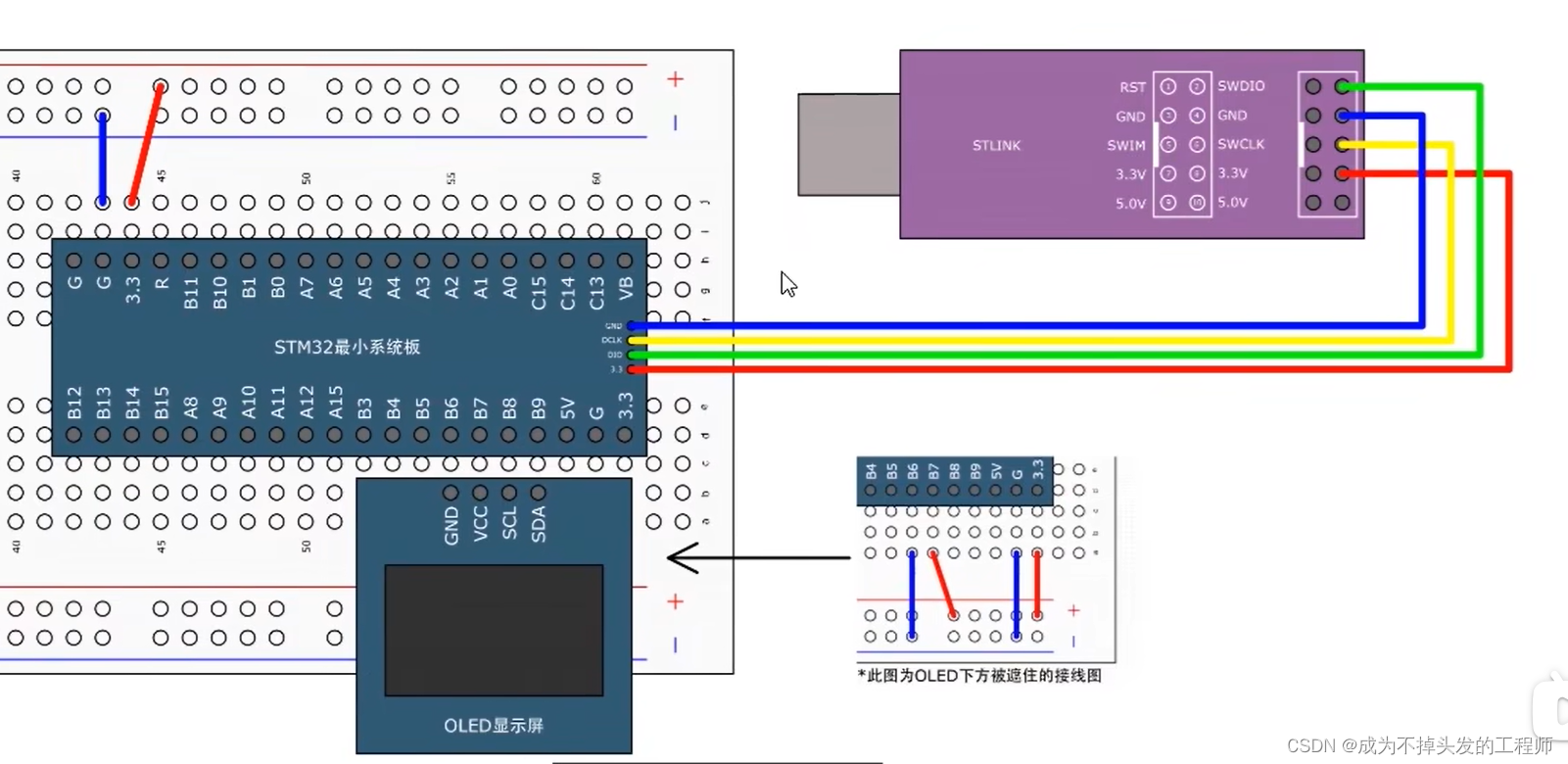
(HAL)STM32F103C6T8——软件模拟I2C驱动0.96寸OLED屏幕
一、电路接法 电路接法参照江科大视频。 二、相关代码及文件 说明:代码采用hal库,通过修改江科大代码实现。仅OLED.c文件关于引脚定义作了hal库修改,并将宏定义OLED_W_SCL(x)、OLED_W_SDA(x)作了相关修改。 1、OLED.c void OLED_I2C_Init(voi…...

分享便携式血氧仪单片机方案
血氧仪主要测量指标分别为脉率、血氧饱和度、灌注指数。血氧饱和度是临床医疗上重要的基础数据之一。以家用指压式血氧仪为例,一个血氧仪一般由MCU、存储芯片、两个控制LED的数模转换器、两个发光二极管驱动等组成。 灵动微电子的MM32MCU产品已被广泛地应用在了一些…...

【Java设计模式】四、适配器模式
文章目录 1、适配器模式2、举例 1、适配器模式 适配器模式Adapter Pattern,是做为两个不兼容的接口之间的桥梁目的是将一个类的接口转换成客户希望的另外一个接口适配器模式可以使得原本由于接口不兼容而不能一起工作的那些类可以一起工作 最后,适配器…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...