代码随想录算法训练营day64 || 84. 柱状图中最大的矩形
单调栈,又一次经典来袭! LeetCode:84.柱状图中最大的矩形_哔哩哔哩_bilibili
首先补充昨天接雨水题目解法的更新,代码随想录 中给出双指针和单调栈的解法,其中所采用的思想是计算每一列可以容纳的雨水,非常的关键,是指导双指针的重要思想。双指针的核心思路是对于每一列,其所容纳的雨水量必定取决于左右两
侧的最高高度,即每一列考虑自身是出于山谷的中间还是两边;这是所有可以容纳雨水的情况;山峰的情况是必定容纳不了雨水的。
而双指针的优化是使用了数组存储各个位置所记录的单边最大高度,有一点动态规划的思想。双指针的求解思路非常的厉害;单调栈也是延续这一个思想,栈内以递增的顺序进行元素的存储。其中出现大于栈顶的元素height[i],再结合栈内一定是栈顶往下递增的,所以此时出现了山谷,那么需要仍然按照列可容纳的思路进行雨水量的累加。
// 减去height[mid]就是所谓的减去高度差的思想
int h = Math.min(height[left], height[index]) - height[mid];
// 计算间隔
int w = index - left - 1;
// 计算剔除了高度差后,目前出栈列与当前i之间可以填入的雨水量
int hold = h * w;
if (hold > 0) sum += hold;stackTop = stack.peek();// 双指针解法真的太厉害了,我个人觉得比单调栈来的神class Solution {public int trap(int[] height) {int length = height.length;if (length <= 2) return 0;int[] maxLeft = new int[length];int[] maxRight = new int[length];// 记录每个柱子左边柱子最大高度maxLeft[0] = height[0];for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);// 记录每个柱子右边柱子最大高度maxRight[length - 1] = height[length - 1];for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);// 求和int sum = 0;for (int i = 0; i < length; i++) {int count = Math.min(maxLeft[i], maxRight[i]) - height[i];if (count > 0) sum += count;}return sum;}
}84. 柱状图中最大的矩形
思路:单调栈,顺序是递减,每一次出栈都将计算当前出栈高度与左右比自己更高的高度所形成矩形面积。通过本题,我们可以得出进栈元素是更新结果的一个边界;由于单调栈的单调特性,因此栈顶的下一个位置的元素是另一个边界,即结果可以通过这三者完成计算。此外采用栈顶元素的下一个位置的元素直接参与计算,那么自然在当前元素出栈后,将会以下一个元素作为栈顶来开展下一此结果更新,那么所谓的高度差的概念,其实是去栈内每一次计算结果时,需要将当前位置的高度与左右两侧边界的高度进行三者的筛选,在接雨水题中,需要用左右两侧的最小值减去当前位置高度得到当前位置的雨水量。而在矩形中,高度差体现在每次更新面积时,height[mid]就是当前高度范围内的最小值,考虑了与(left,right)之间高度的高度比较,即高度差。
class Solution {int largestRectangleArea(int[] heights) {ArrayDeque<Integer> st = new ArrayDeque<>();// 数组扩容,在头和尾各加入一个元素,为了有效的应对heights全员递增或全员递减的情况int [] newHeights = new int[heights.length + 2];newHeights[0] = 0;newHeights[newHeights.length - 1] = 0;for (int index = 0; index < heights.length; index++){newHeights[index + 1] = heights[index];}// 原来的数组指向扩容完成的数组heights = newHeights;st.push(0);int result = 0;// 第一个元素已经入栈,从下标1开始for (int i = 1; i < heights.length; i++) {// 栈内排序是递减的,遇到更大的元素直接进栈if (heights[i] > heights[st.peek()]) {st.push(i);} else if (heights[i] == heights[st.peek()]) {st.pop(); // 加不加都行,因为以相等高度进行求解时,左侧相等的高度不会存在高度差的问题,但是还是出栈比较好,这样减少后续计算量st.push(i);} else {// 注意,从左开始向右进行遍历,则持续出栈的过程中每一次出栈都可以更新结果while (heights[i] < heights[st.peek()]) { // 获取当前高度int mid = st.peek();st.pop();// 获取左侧高度int left = st.peek();// 获取右侧高度int right = i;// 计算长,这一步非常的关键,这里剔除了高度更小的left和right加入计算,而是去已经left与right之间已经出栈的高的高度加入计算// 如果mid是最高的,那么w等于1;如果mid不是最高的,那么(left,right)之间的元素都比height[mid]来的更大int w = right - left - 1;// 当前出栈元素是三个位置内高度最高的,以mid为基准进行面积计算int h = heights[mid];result = Math.max(result, w * h);}st.push(i);}}return result;}
}相关文章:

代码随想录算法训练营day64 || 84. 柱状图中最大的矩形
单调栈,又一次经典来袭! LeetCode:84.柱状图中最大的矩形_哔哩哔哩_bilibili 首先补充昨天接雨水题目解法的更新,代码随想录 中给出双指针和单调栈的解法,其中所采用的思想是计算每一列可以容纳的雨水,非常…...

图的简单介绍
定义及术语 G(V,E):图G的顶点集为V,边集为E。分为有向图和无向图两类。 顶点的度:与该结点相连的边的条数。 出度:顶点的出边条数 入度:顶点的入边条数 顶点的权值称为点权,边的权值称为边权。 存储 1.邻…...
和event(事件))
【C#小知识】c#中的delegate(委托)和event(事件)
今天来介绍一下delegate和event。delegate在c#中可以定义一个函数类型,可以将函数作为一个对象来使用。event在c#中则可以看做一个函数的集合,event中包含了一个或多个函数。 delegate using System;public class MyClass {//定义委托public delegate v…...

车规级存储芯片SPI NOR Flash
国产SPI NOR Flash厂家聚辰提供多种容量选择,可满足多种实时操作系统所需的不同存储空间;并且,拥有四种不同电压范围,分别为3V、1.8V、1.2V以及针对电池供电应用推出的1.65V~3.6V宽压供电的产品系列;同时,提…...
CSS轻松学:简单易懂的CSS基础指南
css基础 更多web开发知识欢迎访问我的专栏>>> 01-CSS初体验 层叠样式表 (Cascading Style Sheets,缩写为 CSS),是一种 样式表 语言,用来描述 HTML 文档的呈现(美化内容)。 书写位置:…...

06 Qt自绘组件:Switch动画开关组件
系列文章目录 01 Qt自定义风格控件的基本原则-CSDN博客 02 从QLabel聊起:自定义控件扩展-图片控件-CSDN博客 03 从QLabel聊起:自定义控件扩展-文本控件-CSDN博客 04 自定义Button组件:令人抓狂的QToolButton文本图标居中问题-CSDN博客 0…...
)
大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)
文章目录 大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)1. 引言1.1 大语言模型(LLM)的重要性及其规模化挑战1.2 分布式训练策略的需求 2. 分布式训练基础原理2.1 并行计算的基本概念与分类 3.…...

98.验证二叉搜索树
98.验证二叉搜索树 思路 1.一开始使用递归,想当前节点满足条件后,再使左右子树分别满足条件。失败,只考虑了节点与左右子树的大小,未考虑隔代节点的关系。 2.转变思路,使用中序遍历的方法,从第一个节点开…...

2月21日,每日信息差
🎖 素材来源官方媒体/网络新闻 🎄 10 家央企签订倡议书:将主动向社会开放人工智能应用场景 🌍 上海成为首个固定资产投资破万亿的一线城市 🌋 特斯拉扩建德国工厂的计划遭当地居民反对 🎁 加拿大公司利用木…...

android.text.BoringLayout.isBoring 的 NullPointerException
都是重写TextView.settext()函数导致的坑~ override fun setText(text: CharSequence?, type: BufferType?) {if (text.isNullOrEmpty()) {return}//业务代码super.setText(text, type)} java.lang.NullPointerException at android.text.BoringLayout.isBoring(BoringLayo…...
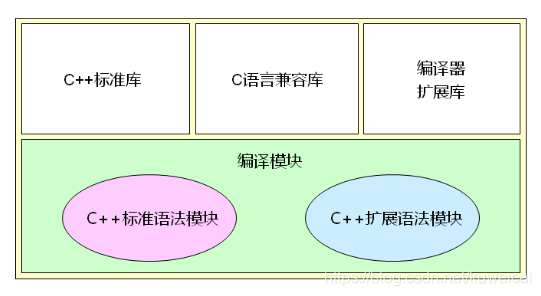
C++ 高频考点
1. C/C内存有哪几种类型? C中,内存分为5个区:堆(malloc)、栈(如局部变量、函数参数)、程序代码区(存放二进制代码)、全局/静态存储区(全局变量、static变量)和常量存储区(常量&…...
Ubuntu安装SVN服务并结合内网穿透实现公网访问本地存储文件
最近,我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念,而且内容风趣幽默。我觉得它对大家可能会有所帮助,所以我在此分享。点击这里跳转到网站。 文章目录 前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svns…...

2月20日,每日信息差
第一、中国联通 1 月智慧客服客户问题解决率为 97.9%,大联接用户达 10.02 亿户,5G 套餐用户约 2.64 亿户,物联网终端连接约 5.06 亿户。5G 行业虚拟专网服务客户数为 9185 个,智慧客服问题解决率 97.9%,智能服务占比 8…...

Visual Studio清单作用
1、作用: 制定程序依赖的C运行库的dll及版本,包括mfc,atl,crt等,在Visual Studio安装目录下的vc/redist下有debug和release版本 2、确定应用程序依赖哪些visual C 库方法: 查看项目-》项目设置-》常规&…...
方法的区别是?hashCode()和equals()的关系是什么?)
Java中的==和equals()方法的区别是?hashCode()和equals()的关系是什么?
目录 解释Java中的和equals()方法。 hashCode()和equals()的关系是什么? 解释Java中的和equals()方法。 在Java中,和equals()方法都用于比较两个对象,但它们在比较时的侧重点和行为上有所不同。 1. **运算符:** - 是Java中的…...

yaml-cpp开源库使用
源码下载:https://github.com/jbeder/yaml-cpp 1.yaml-cpp编译 步骤主要如下:进入源码目录后 mkdir build cd build cmake … make make install 2.代码示例 #include "funset.hpp" #include <string> #include <fstream> #i…...

【C++私房菜】序列式容器的迭代器失效问题
目录 一、list的迭代器失效 二、vector的迭代器失效 1、空间缩小操作 2、空间扩大操作 三、总结 在C中,当对容器进行插入或删除操作时,可能会导致迭代器失效的问题。所谓迭代器失效指的是,原先指向容器中某个元素的迭代器,在…...
MySQL 篇-深入了解 DML、DQL 语言(二)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 DML、DQL 语言说明 2.0 使用 DML 实现对数据管理和操作 2.1 DML - 增添数据 insert 2.2 DML - 修改数据 update 2.3 DML - 删除数据 delete 3.0 使用 DQL 实现对…...
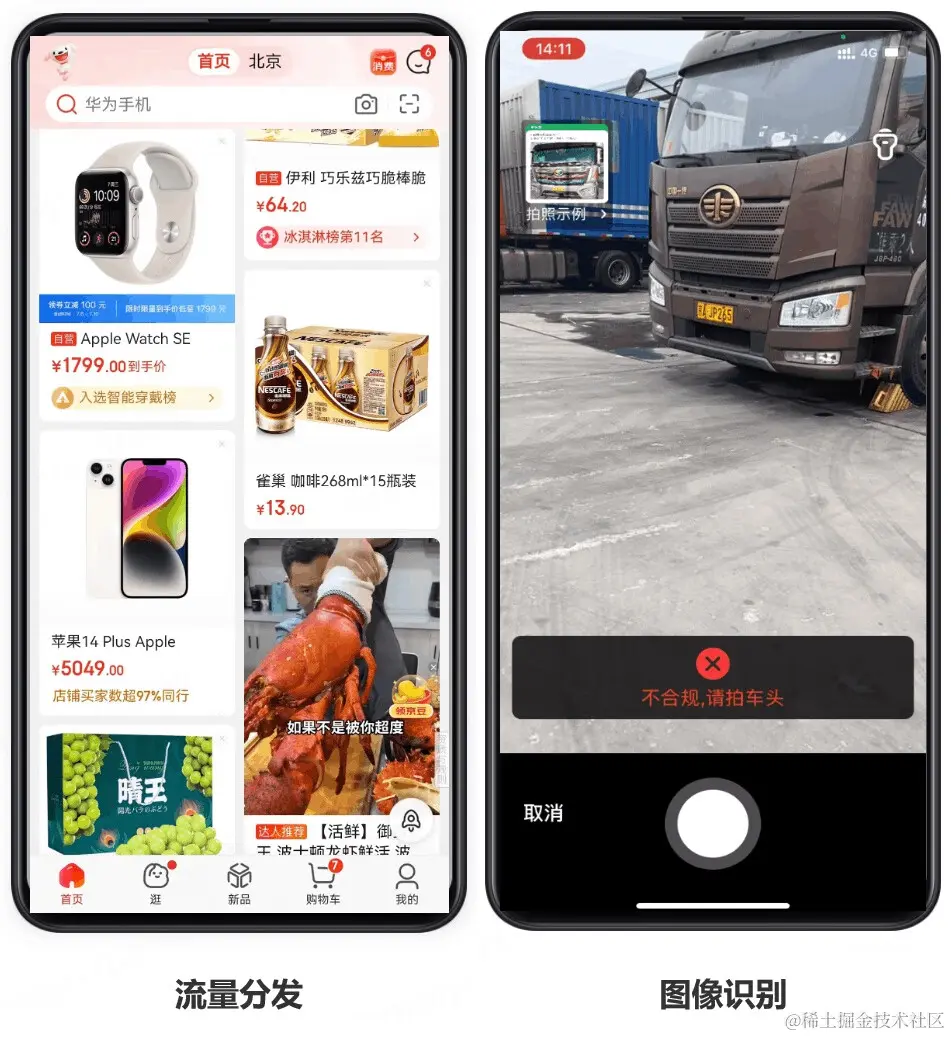
端智能:面向手机计算环境的端云协同AI技术创新
近年来,随着移动端设备软硬件能力的进步,移动端的算力有了很大提升,同时面向移动端的机器学习框架和模型轻量化技术越来越成熟,端上的AI能力逐渐进入大众视野,端智能在电商领域也开始逐步走向规模化应用。通过持续探索…...

PHP函数 “password_hash“ 哈希密码
哈希函数是一种将输入转换为固定长度字符串的方法,这个过程是不可逆的,也就是无法从哈希值还原出原始输入。通过将密码进行哈希处理,即使数据库泄露,攻击者也无法简单地获取到用户密码。 在PHP中,我们可以使用 "…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
