LeetCode 2673.使二叉树所有路径值相等的最小代价:自顶向下的DFS 或 自底向上的递推
【LetMeFly】2673.使二叉树所有路径值相等的最小代价:自顶向下的DFS 或 自底向上的递推
力扣题目链接:https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/
给你一个整数 n 表示一棵 满二叉树 里面节点的数目,节点编号从 1 到 n 。根节点编号为 1 ,树中每个非叶子节点 i 都有两个孩子,分别是左孩子 2 * i 和右孩子 2 * i + 1 。
树中每个节点都有一个值,用下标从 0 开始、长度为 n 的整数数组 cost 表示,其中 cost[i] 是第 i + 1 个节点的值。每次操作,你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。
你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。
注意:
- 满二叉树 指的是一棵树,它满足树中除了叶子节点外每个节点都恰好有 2 个节点,且所有叶子节点距离根节点距离相同。
- 路径值 指的是路径上所有节点的值之和。
示例 1:
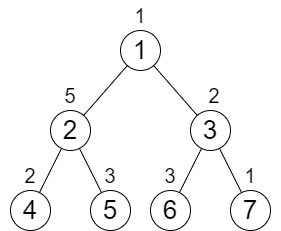
输入:n = 7, cost = [1,5,2,2,3,3,1] 输出:6 解释:我们执行以下的增加操作: - 将节点 4 的值增加一次。 - 将节点 3 的值增加三次。 - 将节点 7 的值增加两次。 从根到叶子的每一条路径值都为 9 。 总共增加次数为 1 + 3 + 2 = 6 。 这是最小的答案。
示例 2:

输入:n = 3, cost = [5,3,3] 输出:0 解释:两条路径已经有相等的路径值,所以不需要执行任何增加操作。
提示:
3 <= n <= 105n + 1是2的幂cost.length == n1 <= cost[i] <= 104
思路
对于某个节点,假设其左子树和右子树都已经“增加”过了(对于左子树,所有路径值相等,右子树同理),但是左子树根到叶路径之和(记为leftSum)和右子树的rightSum不等,我们应该怎么操作呢?
举例说明点我例如如下二叉树中
15 2 2 3 3 1的根节点
1,假设其左子树已经由5 2 3变成了
5 3 3,而右子树已经由
2 3 1变成了
2 3 3那么我们应该如何进行下一步操作呢?
对于根节点
1:其左子树已经平衡,路径之和为5 + 3 = 8;其右子树已经平衡,路径之和为2 + 3 = 5。想要让左右子路径之和相等?当然只要
右子的根节点+3即可。
也就是说:
将左右子树路径和之差加到路径和较小的子树的根节点上。
这是因为“加一操作”越靠近根,所能影响的路径数就越多。
方法一:自顶向下的DFS
首先要说明的是这种方法的空间复杂度不如方法二,但是比方法二更容易理解。
我们只需要写一个函数dfs(n)返回节点n(根节点下标从0开始)为根到叶节点的路径之和:
递归左子树得到
leftSum,递归右子树得到rightSum将
leftSum和rightSum之差累加到答案中返回
max(leftSum, rightSum) + cost[n]作为该节点到叶节点的路径之和终止条件:
n超出数组范围
- 时间复杂度 O ( N ) O(N) O(N),其中 N N N为二叉树节点个数。
- 空间复杂度 O ( log N ) O(\log N) O(logN),满二叉树的深度是 log N \log N logN级别的。
AC代码
C++
class Solution {
private:int ans;int dfs(int n, vector<int>& cost) {if (n >= cost.size()) {return 0;}/*01 23 4 5 6*/int leftSum = dfs(n * 2 + 1, cost);int rightSum = dfs(n * 2 + 2, cost);ans += max(leftSum, rightSum) - min(leftSum, rightSum);return max(leftSum, rightSum) + cost[n];}
public:int minIncrements(int n, vector<int>& cost) {ans = 0;dfs(0, cost);return ans;}
};
方法二:自底向上的递推

在自顶向下的方法一中,递归占用了 O ( N ) O(N) O(N)的空间复杂度。因为往下计算的过程中还要存储当前节点的信息。
因此我们可以倒过来,采用自底向上的方法:
从最后一个非叶节点开始往根节点遍历
这个节点的两个子节点之差累加到答案
这个节点的两个子节点的最大值累加到这个节点(路径累加)
这样相当于是把值存放到 c o s t cost cost数组中了。
- 时间复杂度 O ( N ) O(N) O(N),其中 N N N为二叉树节点个数。
- 空间复杂度 O ( 1 ) O(1) O(1),但是我们修改了 c o s t cost cost数组的值。若其值不能被修改,则空间复杂度为 O ( N ) O(N) O(N)(大于方法一的 O ( log N ) O(\log N) O(logN),因为方法一底部的值向上传递后可以被丢弃)
AC代码
C++
class Solution {
public:int minIncrements(int n, vector<int>& cost) {int ans = 0;for (int i = n / 2 - 1; i >= 0; i--) {ans += abs(cost[i * 2 + 1] - cost[i * 2 + 2]);cost[i] += max(cost[i * 2 + 1], cost[i * 2 + 2]);}return ans;}
};
Python
# from typing import Listclass Solution:def minIncrements(self, n: int, cost: List[int]) -> int:ans = 0for i in range(n // 2 - 1, -1, -1):ans += abs(cost[i * 2 + 1] - cost[i * 2 + 2])cost[i] += max(cost[i * 2 + 1], cost[i * 2 + 2])return ans
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/136357361
相关文章:

LeetCode 2673.使二叉树所有路径值相等的最小代价:自顶向下的DFS 或 自底向上的递推
【LetMeFly】2673.使二叉树所有路径值相等的最小代价:自顶向下的DFS 或 自底向上的递推 力扣题目链接:https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/ 给你一个整数 n 表示一棵 满二叉树 里面节点的数目,节点编…...

9、电源管理入门之CPU Idle
目录 1. CPU Idle有什么用? 2. CPU Idle整体框架 3. Idle状态判断 3. cpuidle core 4. 注册初始化 4.1 cpuidle governor注册 4.2 cpuidle driver注册 4.3 cpuidle device注册 5. cpuidle触发流程 关于Linux的很多知识其实网上的资料非常的多,但是也有些问题: 有时…...

uniapp的扩展组件uni-popup 弹出层自动打开
我的需求是在页面加载完之后自动打开弹窗,自动打开只能写在onReady 或 mounted 生命周期内,这是这个组件的规定: 如果想在页面渲染完毕后就打开 uni-popup ,请在 onReady 或 mounted 生命周期内调用,确保组件渲染完毕…...

二、mysql常用函数
目录 一、Mysql数值型函数 二、Mysql字符串函数 三、Mysql日期和时间函数 四、Mysql聚合函数 五、Mysql流程控制函数 六、其他函数 一、Mysql数值型函数 函数名称 作用 abc 求绝对值 sqrt 求二次方根 mod 求余数 ceil 和 ceiling 功能一样,都是返回不小…...

【Redis | 第一篇】快速了解Redis
文章目录 1.快速了解Redis1.1简介1.2与其他key-value存储的不同处1.3Redis安装——Windows环境1.3.1下载redis1.3.2启动redis1.3.3进入redis客户端1.3.4修改配置 1.4Redis安装——Linux环境1.4.1安装命令1.4.2启动redis1.4.3进入redis客户端 1.5配置修改1.6小结 1.快速了解Redi…...
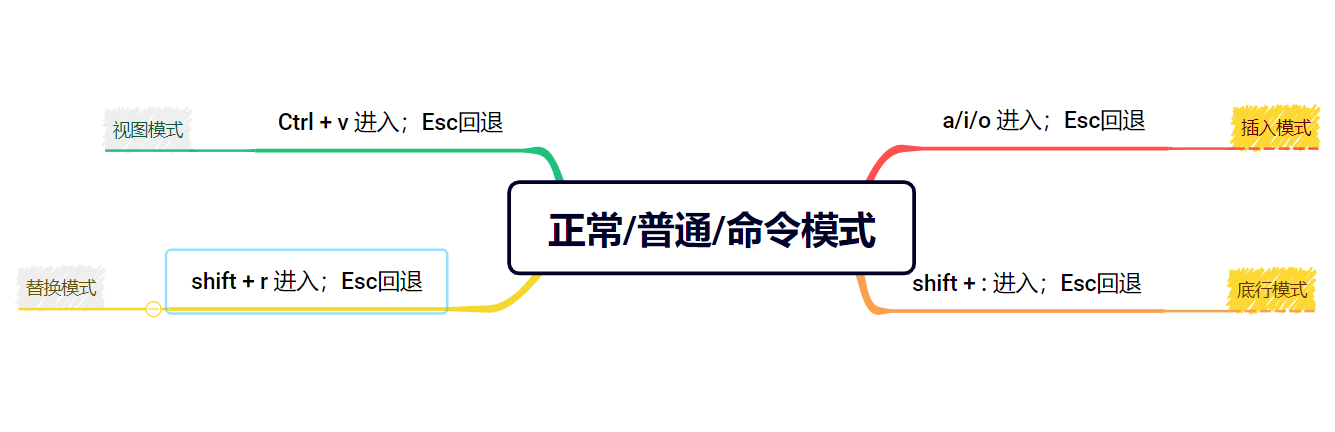
Vim 模式切换 | 命令集
Vim 模式切换 | 命令集 vim 主要模式及切换一、正常/普通/命令模式1 光标相关操作命令集1.1 光标移动1.2 文字删除1.3 粘贴和复制1.4 撤销1.5 字符更改 二、插入模式2.1 插入模式和命令行模式相互切换 三、末行模式2.1 末行模式和命令行模式相互切换2.2 末行模式相关命令集 四、…...

广和通5G智能模组SC171支持Android、Linux和Windows系统,拓宽智能物联网应用
世界移动通信大会2024期间,广和通宣布:5G智能模组SC171除支持Android操作系统外,还兼容Linux和Windows系统,帮助更多智能终端客户快速迭代产品,拓宽智能化应用覆盖范围。 广和通SC171系列基于高通QCM6490物联网解决方案…...
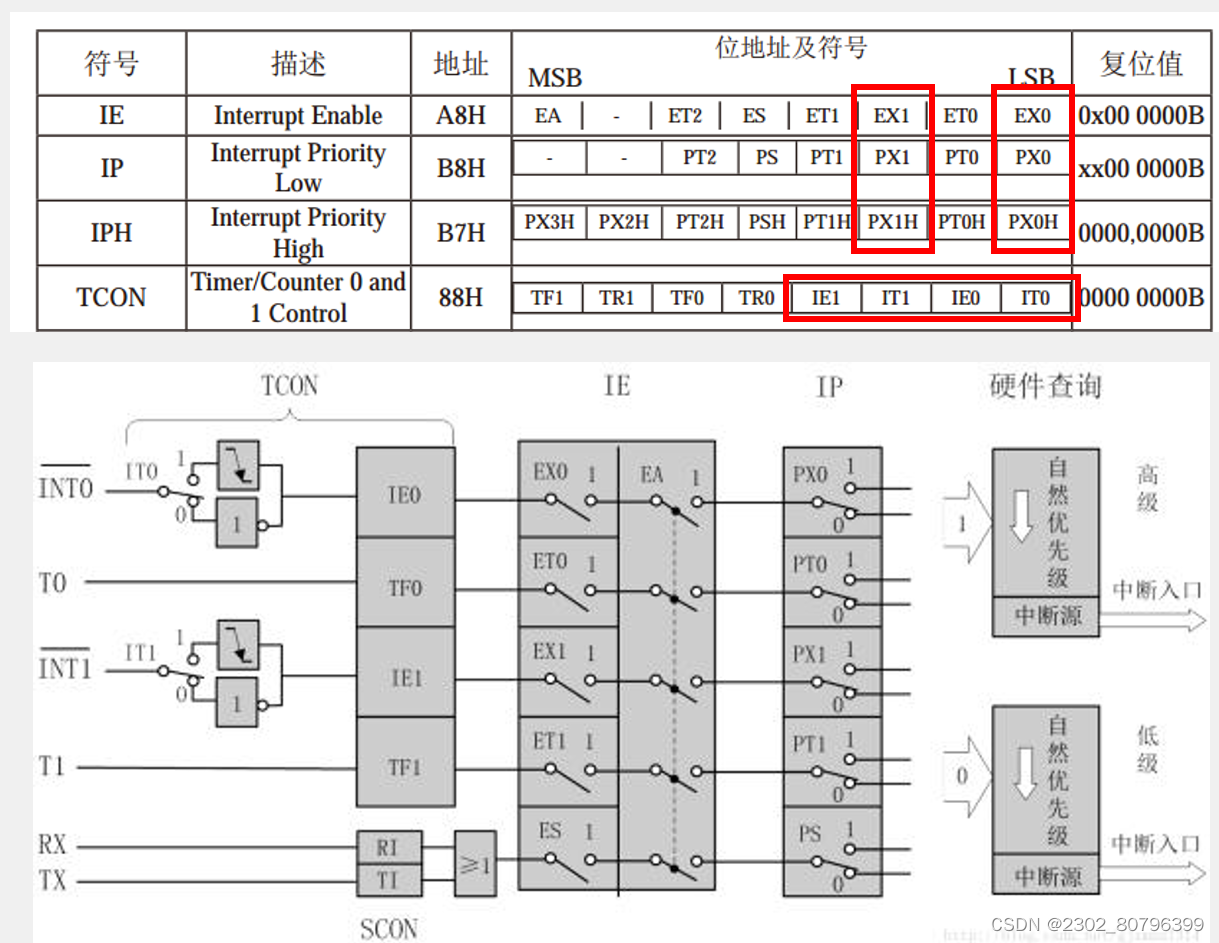
【51单片机】红外遥控红外遥控电机调速(江科大)
1.红外遥控简介 红外遥控是利用红外光进行通信的设备,由红外LED将调制后的信号发出,由专用的红外接收头进行解调输出 通信方式:单工,异步 红外LED波长:940nm 通信协议标准:NEC标准 2.硬件电路 红外发送部分 IN高电平时,LED不亮,IN低电平时&…...
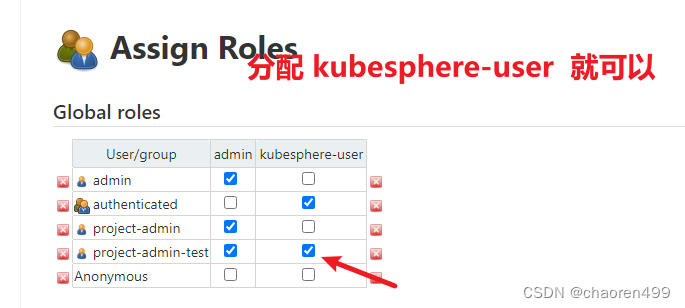
kubesphere jenkins 流水线 未运行(解决方案)
场景: 在kubesphere 中运行 流水线 devops 结果,显示未运行 但是用 admin 账户是可以运行成功的。 问题解决 1- 查日志: 然后 Caused: org.acegisecurity.userdetails.UsernameNotFoundException: org.springframework.security.core.…...

如何保护服务器的安全
互联网的迅速发展,让很多企业都很重视网络技术的使用,但是网络的传播速度比较快,同时容易造成数据、隐私方面的泄露现在每个企业基本有自己的服务器。有几点需要注意,可以参考: 1.基础密码安全 最基本的安全就是密码安…...

Python使用HDL 模拟器实现 FPGA 板卡的仿真验证
Python 结合 HDL 模拟器实现 FPGA 板卡的仿真验证,您可以借助一些开源工具和库来实现这一目的。下面我将为您介绍一种常用的方法,使用 Python 结合 Verilog 模拟器和 FPGA 开发工具进行仿真验证。 ### 步骤概述 1. **编写 Verilog 设计**:首…...

vue中 input disable后无法触发点击事件
问题:input标签为disabled后,点击事项无效;当点击文字**“请选择”**时无法触发点击事件,其父标签的其余位置均可触发 解决:只需要在input标签中添加 style“pointer-events:none” 即可 pointer-events: none 作用是…...

实战一个 Jenkins 构建 CI/CD流水线 的简单配置过程哈
引言:上一期我们讲述了gitlabCI/CD工具的介绍,工具之争,本期我们介绍Jenkins CI/CD 目录 一、Jenkins介绍 1、Jenkins概念 2、Jenkins目的 3、特性 4、产品发布流程 二、安装Jenkins 1、安装JDK 2、安装Jenkins 1、上传压缩包 2、…...
【InternLM 实战营笔记】大模型评测
随着人工智能技术的快速发展, 大规模预训练自然语言模型成为了研究热点和关注焦点。OpenAI于2018年提出了第一代GPT模型,开辟了自然语言模型生成式预训练的路线。沿着这条路线,随后又陆续发布了GPT-2和GPT-3模型。与此同时,谷歌也…...

数据卷(Data Volumes) 自定义镜像(dockerfile)
目录 一. 数据卷(Data Volumes) 1.1 什么是数据卷 1.2 为什么需要数据卷 1.3 数据卷的作用 1.4 数据卷的使用 二. 自定义镜像(dockerfile) 2.1 什么是dockerfile 2.2 自定义centos 2.3 自定义tomcat 一. 数据卷(Data…...
数据库管理-第156期 Oracle Vector DB AI-07(20240227)
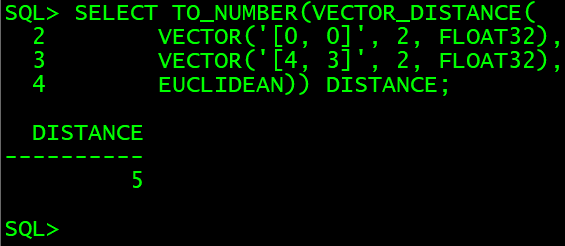
数据库管理156期 2024-02-27 数据库管理-第156期 Oracle Vector DB & AI-07(20240227)1 Vector相关DDL操作可以在现有的表上新增vector数据类型的字段:可以删除包含vector数据类型的列:可以使用CTAS的方式,从其他有…...
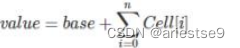
CASAtomic原子操作详解
什么是原子操作?如何实现原子操作? 我们在接触到事务的时候,了解到事务的一大特性是原子性,一个事务要么全部执行、要么全部不执行。 并发里的原子性和事务里的原子性有一样的内涵和概念。假定有2个操作A和B都包含多个步骤…...
真机测试——关于荣耀Magic UI系列HBuilder真机调试检测不到解决办法
出现这种状况怎么办 1、开启USB调试 2、重点来了——我们要选择USB配置,选择音频来源 3、连接OK...

代理IP安全问题:在国外使用代理IP是否安全
目录 前言 一、国外使用代理IP的安全风险 1. 数据泄露 2. 恶意软件 3. 网络攻击 4. 法律风险 二、保护国外使用代理IP的安全方法 1. 选择可信的代理服务器 2. 使用加密协议 3. 定期更新系统和软件 4. 注意网络安全意识 三、案例分析 总结 前言 在互联网时代&…...

SonarLint 疑难语法修正
/*** 投诉率统计(厂端)* 1.通过售后小区分组统计* 2.通过经销商分组统计* param kpiComplaintRateQueryVO 查询参数* return 投诉率统计数据*/ApiOperation(value "厂端投诉率统计维度查询")PostMapping("/vcdc/ratestatis")public List<KpiComplaintR…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
