神经网络系列---计算图基本原理
文章目录
- 计算图
- 符号微分
- 符号微分的步骤
- 示例
- 符号微分在计算图中的使用
- 总结
- 数值微分
- 前向差分法
- 中心差分法
- 数值微分的使用
- 注意事项
- 总结
- 自动微分
- 1. 基本原理
- 2. 主要类型
- 3. 计算图
- 4. 应用
- 5. 工具和库
- 6. 优点和缺点
- 计算图
- 1. **计算图的建立**
- 2. **前向传播**
- 3. **反向传播**
- 4. **链式法则和梯度计算**
- 5. **优点**
- 例子:
- 步骤1: 定义变量和运算
- 步骤2: 创建节点
- 步骤3: 创建边
- 步骤4: 执行前向传播
- 步骤5: (可选)执行反向传播
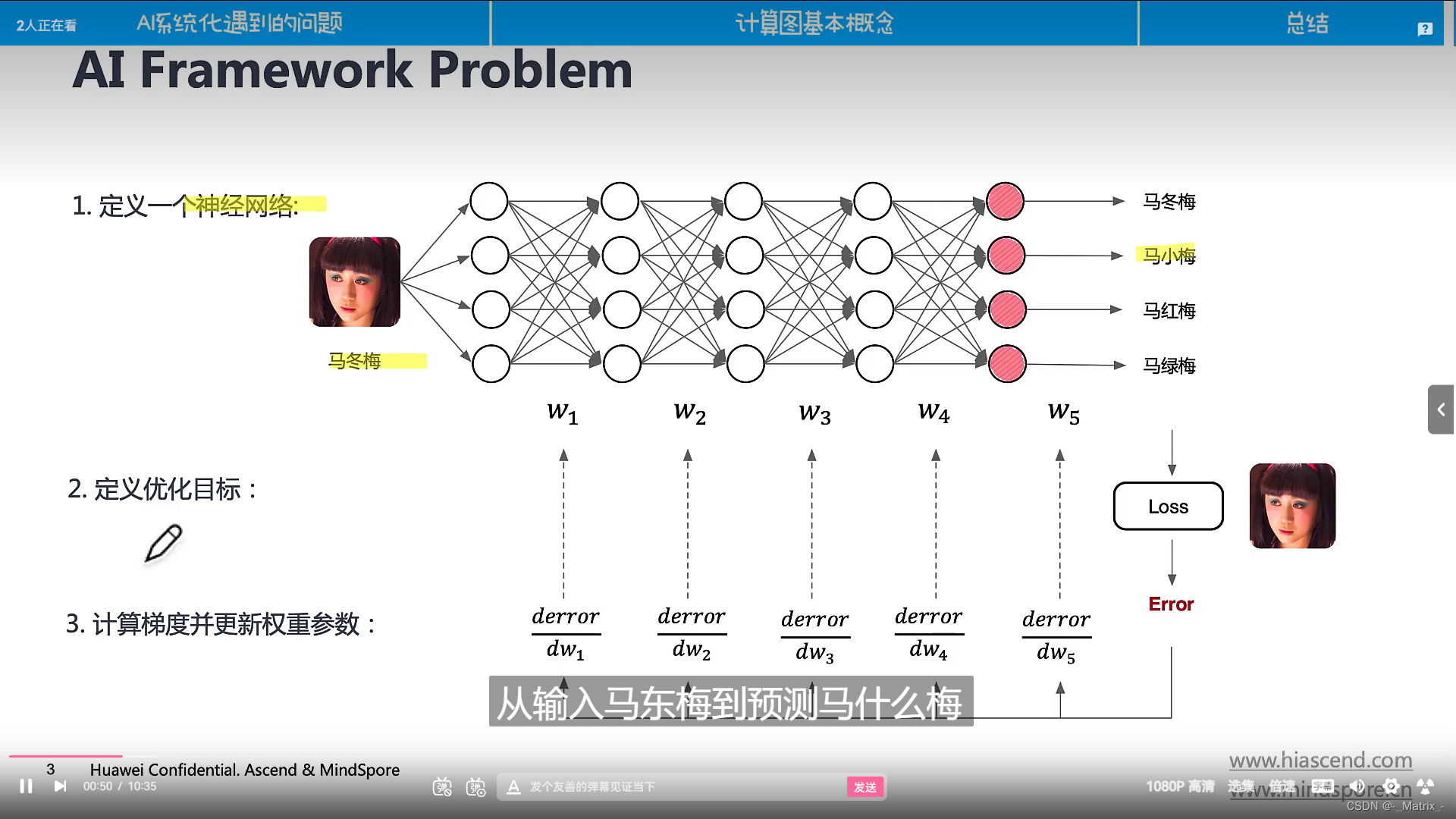
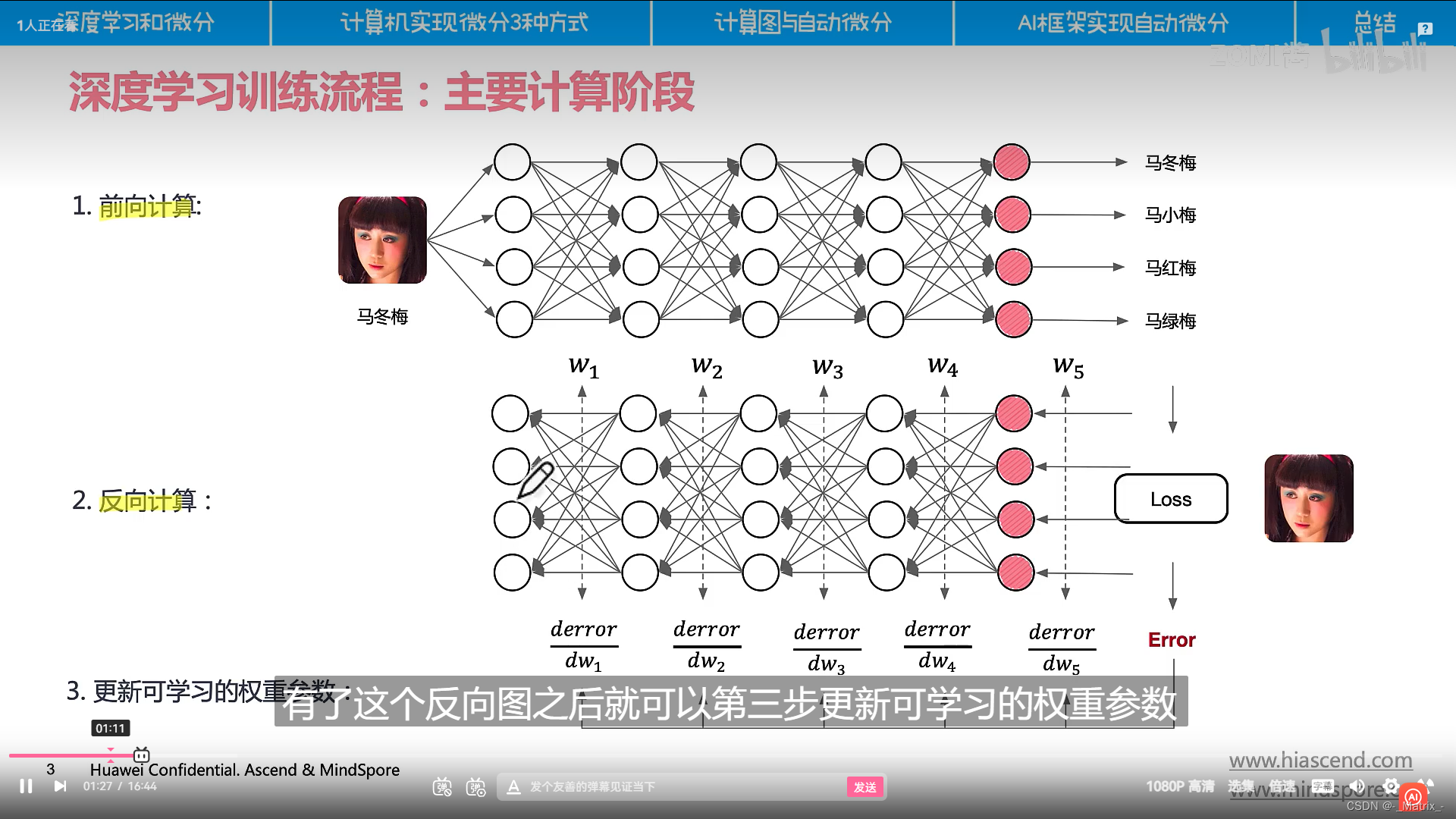
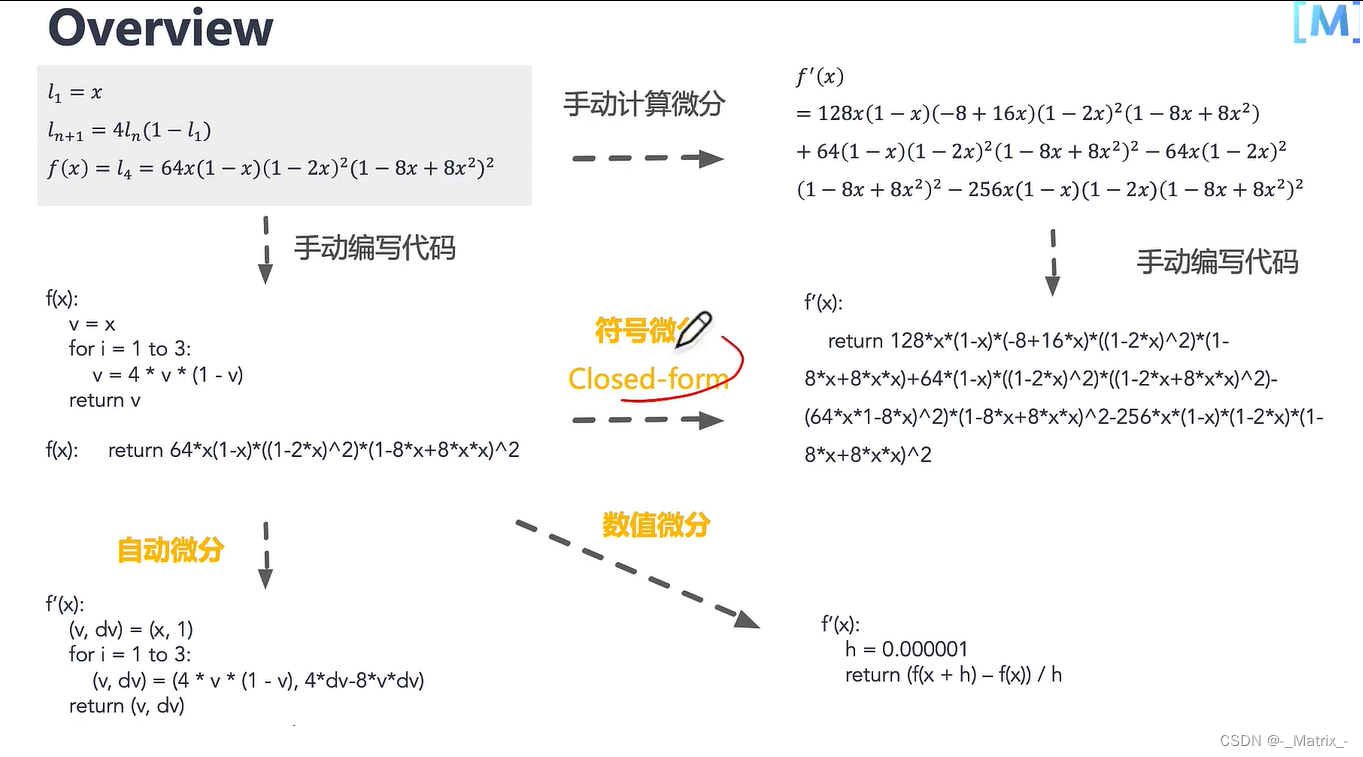
计算图

符号微分

符号微分(Symbolic Differentiation)是一种使用数学表达式来表示微分或导数的技术。与数值微分不同,符号微分不是通过逼近来计算导数,而是直接处理数学表达式,得到一个精确的表达式,表示该函数的导数。
符号微分的步骤
-
表达式定义:首先,你需要一个表达式,例如一个多项式或任何可以微分的数学函数。
-
应用微分规则:然后,你会应用一系列微分规则(如乘积规则、商规则、链式法则等)来对表达式进行微分。
-
简化表达式:最后,你可能需要使用一些代数技巧来简化得到的导数表达式。
示例
假设你有一个函数 f ( x ) = x 2 + 3 x + 2 f(x) = x^2 + 3x + 2 f(x)=x2+3x+2,并且你想要找到其导数。通过符号微分,你可以应用基本的导数规则:
- d d x x n = n ⋅ x n − 1 \frac{d}{dx} x^n = n \cdot x^{n-1} dxdxn=n⋅xn−1
- d d x c = 0 \frac{d}{dx} c = 0 dxdc=0 (其中 c c c 是常数)
- 线性函数的导数等于其系数
这样,你可以找到 f ( x ) f(x) f(x)的导数:
f ′ ( x ) = 2 ⋅ x 1 + 3 ⋅ 1 + 0 = 2 x + 3 f'(x) = 2 \cdot x^1 + 3 \cdot 1 + 0 = 2x + 3 f′(x)=2⋅x1+3⋅1+0=2x+3
符号微分在计算图中的使用
在深度学习中,符号微分经常与计算图结合使用:
- 前向传播:通过计算图表示模型的前向计算。
- 符号微分:应用符号微分来表示每个操作的局部导数。
- 反向传播:使用链式法则和计算图中的局部导数来计算整个模型的梯度。
这个过程允许深度学习框架自动计算模型的梯度,这是训练神经网络时所必需的。
总结
符号微分提供了一种精确、直接的方式来计算导数。在深度学习和其他科学计算应用中,通过结合计算图,符号微分使得自动求导和梯度下降优化变得可行和高效。不过,对于非常复杂的表达式,符号微分可能导致表达式膨胀,从而增加了计算复杂性。因此,有时可能会结合使用符号微分和数值微分方法。
数值微分

数值微分是一种近似计算函数导数的技术。与符号微分不同,数值微分不是通过解析地处理数学表达式来找到导数的精确形式,而是使用函数在特定点的数值来估计导数。
前向差分法
最简单的数值微分方法之一是前向差分法。假设你想要计算函数 f ( x ) f(x) f(x)在点 x x x处的导数,你可以使用以下公式:
f ′ ( x ) ≈ f ( x + h ) − f ( x ) h f'(x) \approx \frac{f(x + h) - f(x)}{h} f′(x)≈hf(x+h)−f(x)
其中 h h h是一个非常小的正数,称为步长。这个公式给出了在 x x x附近的函数的斜率的近似值。
中心差分法
前向差分方法的一个问题是,它可能不是非常精确,特别是当 h h h相对较大时。更精确的方法是中心差分法,使用以下公式:
f ′ ( x ) ≈ f ( x + h ) − f ( x − h ) 2 h f'(x) \approx \frac{f(x + h) - f(x - h)}{2h} f′(x)≈2hf(x+h)−f(x−h)
中心差分通过计算 f ( x ) f(x) f(x)在 x x x附近的两点的平均斜率,通常提供了更好的近似。
数值微分的使用
数值微分用于许多不同的应用领域,包括:
-
解析解不可用:当函数的导数很难或不可能解析地找到时,可以使用数值微分。
-
深度学习的梯度检查:在深度学习中,数值微分通常用于梯度检查,以确保使用符号微分(或自动微分)计算的梯度是正确的。
-
科学和工程应用:数值微分用于许多科学和工程应用,其中需要近似导数,但可能没有解析解。
注意事项
-
选择步长:选择合适的步长 h h h是一个关键问题。太大的步长可能会导致近似不精确,而太小的步长可能会导致数值不稳定。
-
数值不稳定:当涉及极小或极大的值时,数值微分可能会出现问题,因为计算机浮点数的精度有限。
-
计算成本:数值微分通常比符号微分更慢,因为它需要多次评估函数。
总结
数值微分是一种有用的工具,特别是当解析解不可用或难以获得时。它提供了一种灵活而实用的方法来近似导数,但必须谨慎选择参数并注意可能的数值问题。在深度学习和其他领域,它通常与符号微分或自动微分结合使用。
自动微分
视频链接:【前向微分和正向微分怎么理解?
自动微分(Automatic Differentiation,简称AD)是一种高效计算函数导数(或梯度)的技术。它不同于数值微分和符号微分,因为它可以提供更高的数值稳定性和计算效率。下面是自动微分的更多细节:
1. 基本原理
自动微分基于链式法则进行,它通过计算机程序来逐步计算和追踪函数的局部导数。基本的想法是将复杂函数分解为一系列简单的元素函数(例如加法、乘法等),并依次计算这些函数的导数。
2. 主要类型
自动微分可以分为两种主要类型:
- 前向模式(Forward Mode)
在前向模式中,我们从输入向量开始,然后通过每一个操作前进,计算每一步的局部导数和全局雅可比矩阵的相应部分。给定一个函数 f : R n → R m f: \mathbb{R}^n \rightarrow \mathbb{R}^m f:Rn→Rm,前向模式特别适合 n ≪ m n \ll m n≪m 的情况。
- 反向模式(Reverse Mode)
在反向模式中,我们首先进行一次正向传递来计算函数的输出,然后从输出向后进行一次传递来计算梯度或雅可比矩阵的每一部分。反向模式特别适合于 n ≫ m n \gg m n≫m 的情况,这也是为什么它被广泛应用于神经网络和深度学习,因为我们通常有许多输入和少量输出(例如损失函数)。
3. 计算图
自动微分常常依赖于一个计算图来表示和跟踪函数的计算过程。计算图是一种图形数据结构,其中每个节点代表一个操作,每个边代表数据流。
4. 应用
自动微分被广泛应用于各种领域,特别是在机器学习和优化问题中。它是训练神经网络时所用的反向传播算法的核心。
5. 工具和库
现有许多库和框架支持自动微分,如TensorFlow、PyTorch等,它们提供了方便的API来实现和使用自动微分技术。
6. 优点和缺点
- 优点:
- 高数值稳定性:比数值微分更稳定。
- 高效:特别是反向模式,它可以高效地计算梯度,尤其是对于有大量输入和少量输出的函数。
- 缺点:
- 内存消耗:反向模式可能需要大量的内存来存储中间结果。
- 实现复杂性:实现一个自动微分系统可能是非常复杂和技术性的。
计算图
自动微分通常是在计算图的基础上实现的。在计算图中,一个复杂函数被分解为多个简单的操作,这些操作被组织为一个有向图。现在,让我们更详细地了解自动微分和计算图之间的关系:
1. 计算图的建立
如我们前面所述,首先我们需要建立一个计算图,代表我们的函数。这涉及将函数分解为更简单的操作和变量,然后以有向图的形式表示这些操作和变量。
2. 前向传播
在计算图中,我们从输入变量开始,然后按照图中的顺序进行操作,直到我们计算出输出。这就是所谓的前向传播。
3. 反向传播
反向传播是自动微分的核心。在这一步,我们从输出开始,然后向后计算每一步的局部导数(或梯度)。这通常涉及应用链式法则,这是一种从输出向输入反向传播导数的方法。
4. 链式法则和梯度计算
通过使用链式法则,我们可以计算从输出到任何中间变量或输入的梯度。通过这种方式,我们可以得到我们想要的所有导数,而不是仅仅是输出相对于输入的导数。
5. 优点
- 精确度:自动微分可以提供与解析解几乎相同的精确度。
- 效率:它通常比数值微分方法更快、更稳定,尤其是对于具有许多变量的复杂函数。
例子:
使用给定的函数 f ( x , y ) = log ( x ) + x ⋅ y − sin ( y ) f(x, y) = \log(x) + x \cdot y - \sin(y) f(x,y)=log(x)+x⋅y−sin(y),我们可以构建一个计算图,将该函数分解为多个基本操作。下面是计算图的创建步骤:
步骤1: 定义变量和运算
首先,我们识别并定义所有的基本变量和运算:
- 变量: x x x, y y y
- 运算:
- log ( x ) \log(x) log(x)
- x ⋅ y x \cdot y x⋅y
- sin ( y ) \sin(y) sin(y)
- 加法和减法来组合上述结果
步骤2: 创建节点
然后,为每个变量和运算创建节点:
- 节点1(变量): x x x
- 节点2(变量): y y y
- 节点3(运算): log ( x ) \log(x) log(x)
- 节点4(运算): x ⋅ y x \cdot y x⋅y
- 节点5(运算): sin ( y ) \sin(y) sin(y)
- 节点6(运算): log ( x ) + x ⋅ y \log(x) + x \cdot y log(x)+x⋅y
- 节点7(运算): log ( x ) + x ⋅ y − sin ( y ) \log(x) + x \cdot y - \sin(y) log(x)+x⋅y−sin(y) (这是最终的输出节点)
步骤3: 创建边
接着,我们连接相应的边来形成有向图:
- 从节点1到节点3(表示 log ( x ) \log(x) log(x) 的输入是 x x x)
- 从节点1到节点4(表示 x ⋅ y x \cdot y x⋅y 的一个输入是 x x x)
- 从节点2到节点4(表示 x ⋅ y x \cdot y x⋅y 的另一个输入是 y y y)
- 从节点2到节点5(表示 sin ( y ) \sin(y) sin(y) 的输入是 y y y)
- 从节点3和节点4到节点6(表示他们的结果被加在一起)
- 从节点6和节点5到节点7(表示前者的结果减去后者的结果来得到最终输出)
步骤4: 执行前向传播
现在你可以执行前向传播来计算输出,按照操作的顺序一步步前进,直到达到输出节点。
步骤5: (可选)执行反向传播
如果你还打算进行自动微分,你可以实施反向传播算法来计算相对于 x x x 和 y y y 的偏导数。
代码实现:
///
/// \brief The Variable class
/// 自动微分
class Variable
{
public://保存值double value;//保存梯度double grad;//当前的梯度是否启用bool isEnableGrad;Variable(double v = 0.0,bool requires_grad=true,double g=0.0) : value(v), isEnableGrad(requires_grad),grad(g){}std::function<void()> backpropFunc;std::vector<std::shared_ptr<Variable>> parents;//设置求导函数void setBackprop(const std::function<void()>& func){backpropFunc = func;}//添加组成当前节点的节点void addParent(const std::shared_ptr<Variable>& parent){parents.push_back(parent);}//反向传播void backward(){if (backpropFunc)backpropFunc();for (auto& parent : parents){parent->backward();}}};//加法
inline std::shared_ptr<Variable> operator+(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value + b->value);result->setBackprop([=]() {if(a->isEnableGrad)a->grad += result->grad;if (b->isEnableGrad)b->grad += result->grad;});result->addParent(a);result->addParent(b);return result;
}
//减法
inline std::shared_ptr<Variable> operator-(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value - b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += result->grad;if (b->isEnableGrad)b->grad -= result->grad;});result->addParent(a);result->addParent(b);return result;
}//乘法
inline std::shared_ptr<Variable> operator*(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value * b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += b->value * result->grad;if (b->isEnableGrad)b->grad += a->value * result->grad;});result->addParent(a);result->addParent(b);return result;
}
// 除法
inline std::shared_ptr<Variable> operator/(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{if (b->value == 0.0) {std::cerr << "Error: Division by zero!" << std::endl;exit(1);}auto result = std::make_shared<Variable>(a->value / b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += (1.0 / b->value) * result->grad;if (b->isEnableGrad)b->grad -= (a->value / (b->value * b->value)) * result->grad;});result->addParent(a);result->addParent(b);return result;
}
// sin
inline std::shared_ptr<Variable> sin(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::sin(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += std::cos(a->value) * result->grad;});result->addParent(a);return result;
}
// cos
inline std::shared_ptr<Variable> cos(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::cos(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad -= std::sin(a->value) * result->grad; // 注意这里是减号,因为cos的导数是-sin});result->addParent(a);return result;
}// log
inline std::shared_ptr<Variable> log(const std::shared_ptr<Variable>& a)
{if (a->value <= 0.0) {std::cerr << "Error: Logarithm of non-positive number!" << std::endl;exit(1);}auto result = std::make_shared<Variable>(std::log(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += (1.0 / a->value) * result->grad; // 导数为 1/x});result->addParent(a);return result;
}// exp
inline std::shared_ptr<Variable> exp(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::exp(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += std::exp(a->value) * result->grad; // 导数为 e^x});result->addParent(a);return result;
}int main() {auto x = std::make_shared<Variable>(2.0); // 创建一个初值为2的变量xauto y = std::make_shared<Variable>(5.0,false); // false 不计算y的梯度auto g = log(x) + x * y - sin(y);g->grad = 1.0; // df/df = 1g->backward();std::cout << "df/dx = " << x->grad << std::endl;std::cout << "df/dy = " << y->grad << std::endl;return 0;
}

相关文章:

神经网络系列---计算图基本原理
文章目录 计算图符号微分符号微分的步骤示例符号微分在计算图中的使用总结 数值微分前向差分法中心差分法数值微分的使用注意事项总结 自动微分1. 基本原理2. 主要类型3. 计算图4. 应用5. 工具和库6. 优点和缺点 计算图1. **计算图的建立**2. **前向传播**3. **反向传播**4. **…...

3D数字孪生
数字孪生(Digital Twin)是物理对象、流程或系统的虚拟复制品,用于监控、分析和优化现实世界的对应物。 这些数字孪生在制造、工程和城市规划等领域变得越来越重要,因为它们使我们能够在现实世界中实施改变之前模拟和测试不同的场景…...
C++惯用法之空基类优化
相关系列文章 C惯用法之Pimpl C惯用法之CRTP(奇异递归模板模式) C之std::tuple(二) : 揭秘底层实现原理 目录 1.空类 2.空基类优化 3.内存布局原则 4.实例分析 5.总结 1.空类 C 中每个对象的实例都可以通过取地址运算符获取其在内存布局中的开始位置,因此每个类…...
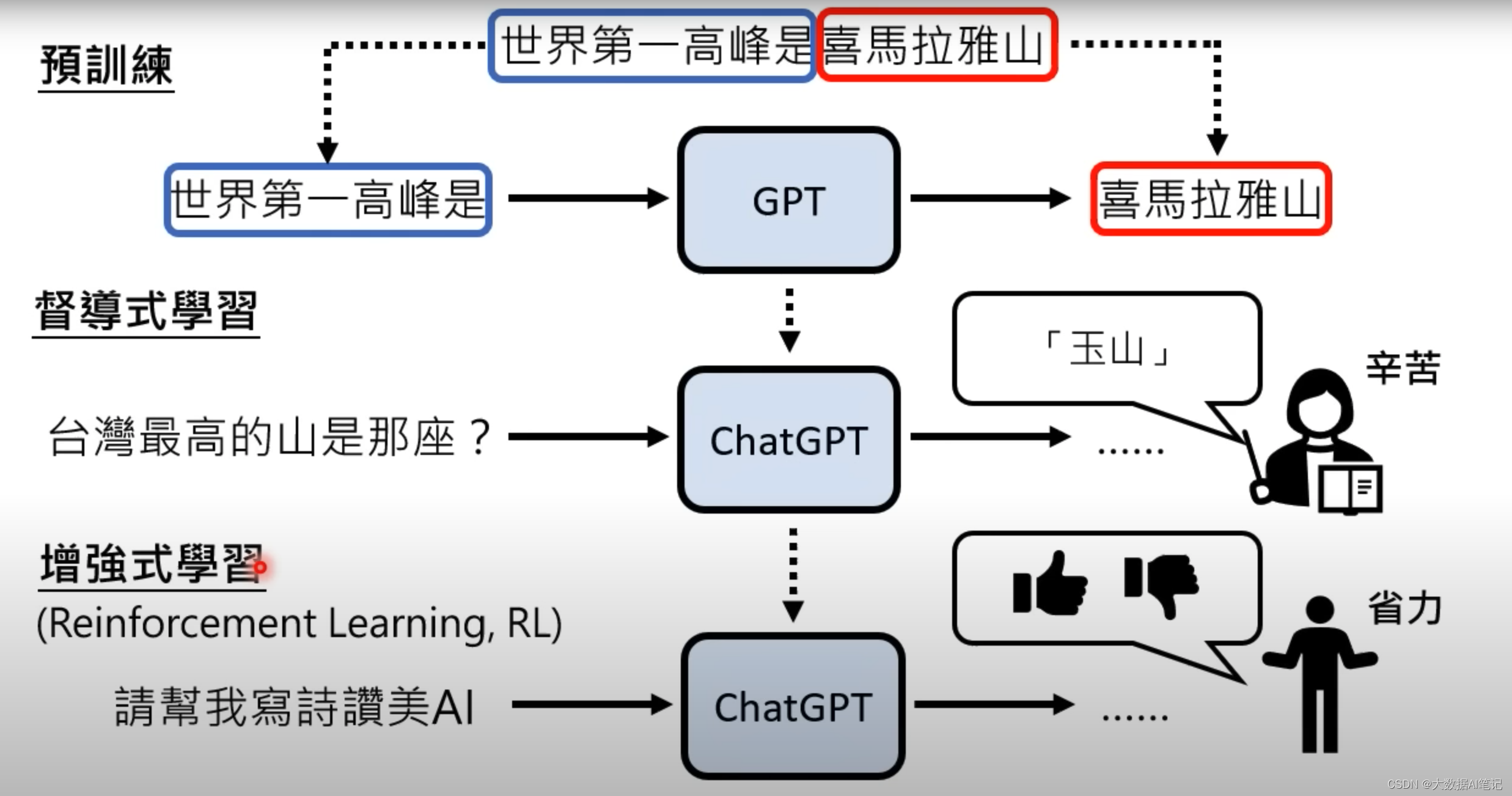
【生成式AI】ChatGPT 原理解析(2/3)- 预训练 Pre-train
Hung-yi Lee 课件整理 预训练得到的模型我们叫自监督学习模型(Self-supervised Learning),也叫基石模型(foundation modle)。 文章目录 机器是怎么学习的ChatGPT里面的监督学习GPT-2GPT-3和GPT-3.5GPTChatGPT支持多语言…...
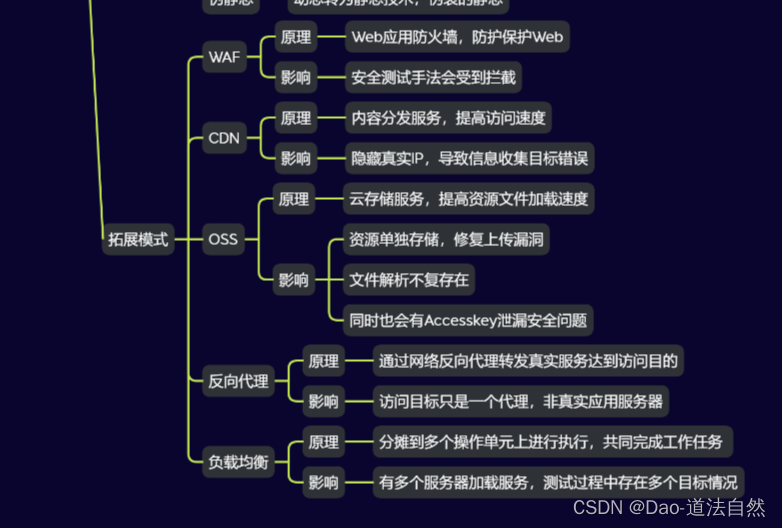
Day03:Web架构OSS存储负载均衡CDN加速反向代理WAF防护
目录 WAF CDN OSS 反向代理 负载均衡 思维导图 章节知识点: 应用架构:Web/APP/云应用/三方服务/负载均衡等 安全产品:CDN/WAF/IDS/IPS/蜜罐/防火墙/杀毒等 渗透命令:文件上传下载/端口服务/Shell反弹等 抓包技术:…...
C++多线程同步(上)
多线程同步 引言总述详情互斥锁示例运行结果分析条件变量示例一实现分析优化运行结果示例二实现代码运行结果示例三实现代码运行结果读写锁示例实现代码注意分析运行结果附言实现运行结果运行结果个人心得引言 项目中使用多线程,会遇到两种问题,一种是对共享资源的访问时需要…...

猜猜心里数字(个人学习笔记黑马学习)
1.定义一个变量,数字类型,内容随意 2.基于input语句输入猜想的数字,通过if和多次elif的组合,判断猜想数字是否和心里数字一致 num5if int(input("请输入第一次猜想的数字:"))5:print("猜对了࿰…...

实用Pycharm插件
Pycharm的离线安装:https://plugins.jetbrains.com/ 需要根据对应的Pycharm/Goland版本选取所需的 对于实用的插件如下: 实时查看每一行的git blame信息: Gittoolbox 转换IDE的英文为中文:Chinese IDE侧格式化json字符串&#…...

数据结构试题练习
(1). 假如队列未满,现有变量data需要入队,请写出表达式; if( (tail1)%SEQLEN ! head ) {seqn[tail] data;tail (tail1)%SEQLEN; } (2). 假如队列未空,现在需要从队列取一个元素并赋值给变量data,请写出表达式; if( head ! tail ) {data se…...
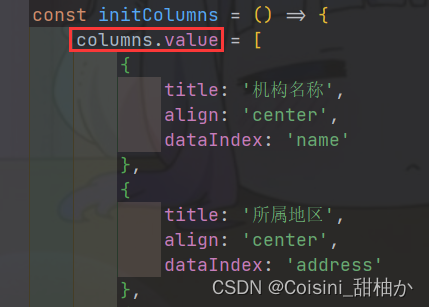
s-table和columns初始化不完整,造成table文件的filter报错
问题 顺藤摸瓜找errorHandler.js文件 发现文件并没有什么问题 顺藤摸瓜找index.vue文件 首先找到报错的filter,发现与columnsSetting相关 找到columnsSetting发现等于columns 返回自己使用S-table组件的地方,发现columns初始化时仅初始化为ref()未表明…...

SLA 是什么?如何实现 SLA 管理
随着业务的不断壮大,为了满足日益增长的客户需求,网络必须保持与这些需求同步。同时,为了提高最终用户的体验,运维人员/网络管理员在监控企业级网络时遇到了不少瓶颈,必须不断审查网络,以确保提供的服务质量…...

火灾安全护航:火灾监测报警摄像机助力建筑安全
火灾是建筑安全中最常见也最具破坏力的灾难之一,为了及时发现火灾、减少火灾造成的损失,火灾监测报警摄像机应运而生,成为建筑防火安全的重要技术装备。 火灾监测报警摄像机采用高清晰度摄像头和智能识别系统,能够全天候监测建筑内…...

JavaScript 基础学习笔记(五):函数、作用域、匿名函数
目录 一、函数 1.1 声明和调用 1.2 形参和实参 1.3 返回值 二、作用域 2.1 全局作用域 2.2 局部作用域 三、匿名函数 3.1 函数表达式 3.2 立即执行函数 一、函数 理解函数的封装特性,掌握函数的语法规则 1.1 声明和调用 函数可以把具有相同或相似逻辑的代…...

Qt环境配置VTK
Qt与VTK的结合为开发者提供了强大的跨平台图形界面开发能力和三维可视化处理能力。本教程旨在详细介绍如何配置Qt环境以使用VTK库,从而为开发者打造高效、强大的三维可视化应用。 一、准备工作 在开始之前,确保您的开发环境中已经安装了Qt和CMake。Qt提…...
腾讯云最新活动_腾讯云促销优惠_代金券-腾讯云官网入口
腾讯云服务器多少钱一年?62元一年起,2核2G3M配置,腾讯云2核4G5M轻量应用服务器218元一年、756元3年,4核16G12M服务器32元1个月、312元一年,8核32G22M服务器115元1个月、345元3个月,腾讯云服务器网txyfwq.co…...

如何创建自己的Spring Boot Starter并为其编写单元测试
当我们想要封装一些自定义功能给别人使用的时候,创建Spring Boot Starter的形式是最好的实现方式。如果您还不会构建自己的Spring Boot Starter的话,本文将带你一起创建一个自己的Spring Boot Starter。 快速入门 创建一个新的 Maven 项目。第三方封装的…...

数据分析---常见处理逻辑
目录 数据清洗数据转换数据聚合数据筛选增删改查(以查为例)数据清洗 去除重复值:使用DISTINCT关键字去除重复行。//这将返回一个包含所有不重复城市的结果集 SELECT DISTINCT city FROM students;处理缺失值:使用IS NULL或IS NOT NULL判断是否为空值,并使用COALESCE或CASE…...
)
2024-02-26(金融AI行业概览与大数据生态圈)
1.最开始的风控是怎么做的? 人审 吃业务经验 不能大批量处理,效率低下 不适用于移动互联网的金融场景 2.建模的概念 建模就是构造一个数学公式,能将我们手上有的数据输入进去,通过计算得到一些预测结果。 比如初高中学习的…...
git忽略某些文件(夹)更改说明
概述 在项目中,常有需要忽略的文件、文件夹提交到代码仓库中,在此做个笔录。 一、在项目根目录内新建文本文件,并重命名为.gitignore,该文件语法如下 # 以#开始的行,被视为注释. # 忽略掉所有文件名是 a.txt的文件. a.txt # 忽略所有生成的 java文件, *.java # a.j…...

python爬虫实战:获取电子邮件和联系人信息
引言 在数字时代,电子邮件和联系人信息成为了许多企业和个人重要的资源,在本文中,我们将探讨如何使用Python爬虫从网页中提取电子邮件和联系人信息,并附上示例代码。 目录 引言 二、准备工作 你可以使用以下命令来安装这些库&a…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
