Linux Shell脚本练习(一)
一、 Linux下执行Shell脚本的方式:
1、用shell程序执行脚本:
a、根据你的shell脚本的类型,选择shell程序,常用的有sh,bash,tcsh等
b、程序的第一行#!/bin/bash里面指明了shell类型的,比如#!/bin/bash指明是bash,#!/bin/sh则是sh;
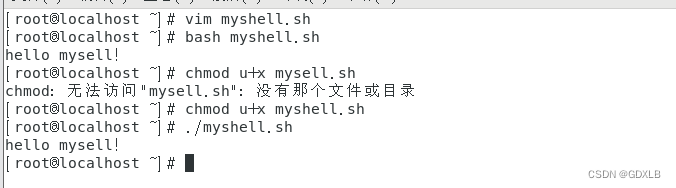
c、然后输入命令(其中bash为shell的名称,myshell.sh则为你要执行的代码):bash myshell.sh
2、直接执行脚本:
a、不过首先的加上可执行权限(也许要root权限,4情况而定)
执行:chmod u+x myshell.sh
b、然后执行:./myshell.sh (或者sh myshell.sh)就可以执行了。
二、编写一个脚本,它能够显示:
序列前10个数字:0、1、1、2、3、5、8、13、…。


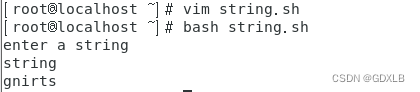
三、写个shell脚本来把字符串反过来显示:
例如:给定abcde 输出edcba

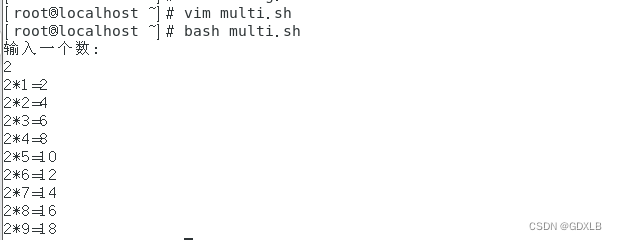
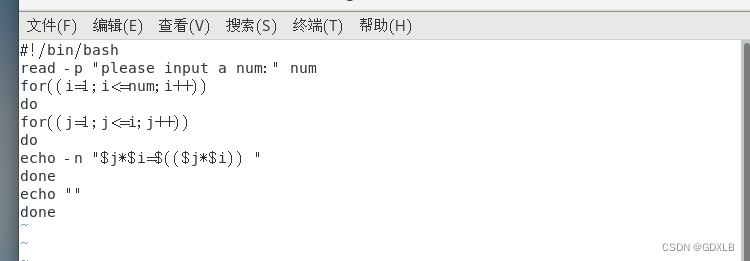
四、编写一个shell脚本,打印任何数的乘法表:
例如,如果你执行此脚本,它应请求一个数,并显示它的表。显示例输出如下:
2*1 = 2
2*2 = 4
…
2*9 = 18


五、利用while循环完成输出循环10次内容:




相关文章:

Linux Shell脚本练习(一)
一、 Linux下执行Shell脚本的方式: 1、用shell程序执行脚本: a、根据你的shell脚本的类型,选择shell程序,常用的有sh,bash,tcsh等 b、程序的第一行#!/bin/bash里面指明了shell类型的,比如#!/…...
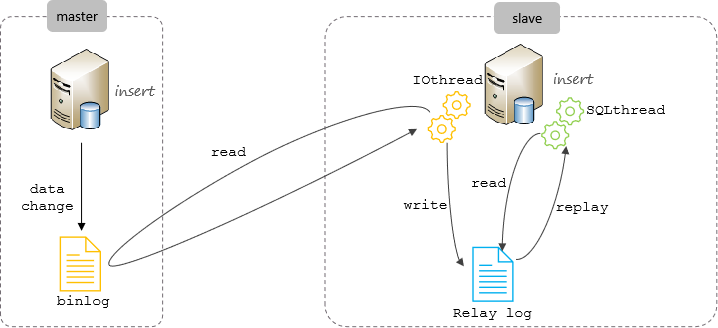
面试数据库篇(mysql)- 11主从同步
原理 MySQL主从复制的核心就是二进制日志 二进制日志(BINLOG)记录了所有的 DDL(数据定义语言)语句和 DML(数据操纵语言)语句,但不包括数据查询(SELECT、SHOW)语句。 复…...

Python中的os库
一.OS库简介 OS是Operating System的简写,即操作系统。 OS库是一个操作系统接口模块,提供一些方便使用操作系统相关功能的函数。 二.OS库常用函数 2.1文件和目录 2.1.1:os.getcwd() 作用:返回当前工作目录,结果是…...

C++ | 使用正则表达式匹配特定形式的字符串
C | 使用正则表达式匹配特定形式的字符串 在 C 中,可以使用 <regex> 头文件提供的正则表达式库来对特定形式的字符串进行匹配操作。 常用的正则表达式模式语法 普通字符: 普通字符会按照其字面意义进行匹配,例如 a 会匹配字符 a。 转…...

计算机组成原理-第一/二章 概述和数据的表示和运算【期末复习|考研复习】
文章目录 前言第一章 计算机组成原理 概述及各种码1.1 计算机硬件的基本组成1.1.1 存储器1.1.2 运算器1.1.3 控制器 1.2 计算机的工作过程1.3 计算机的性能指标1.4 各个字长区别与联系 第二章 数据的表示与运算2.1 ASCII码2.2 各种码2.3 浮点数 总结 前言 给大家整理了一下计算…...

基于transform的scale属性,动态缩放整个页面,实现数据可视化大屏自适应,保持比例不变形,满足不同分辨率的需求
文章目录 一、需求背景:二、需求分析:三、选择方案:四、实现代码:五、效果预览:六、封装组件: 一、需求背景: 数据可视化大屏是一种将数据、信息和可视化效果集中展示在一块或多块大屏幕上的技…...
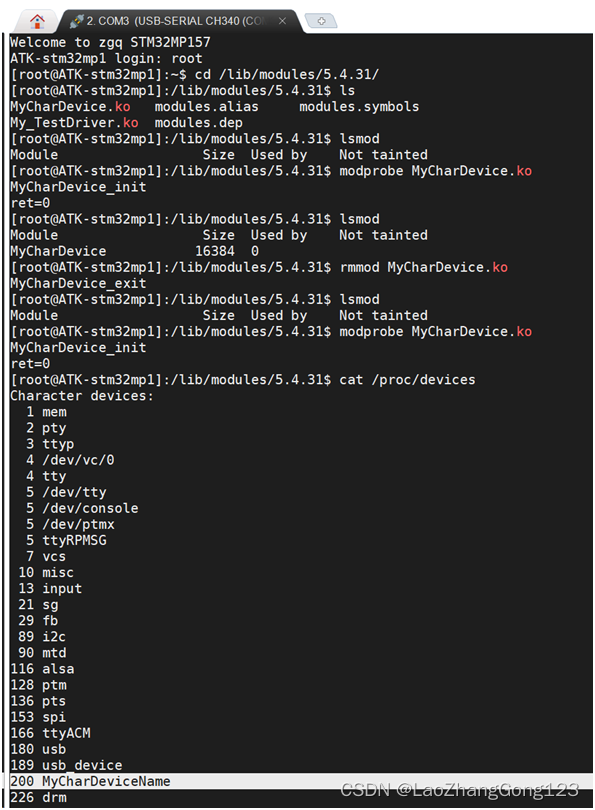
Linux第67步_linux字符设备驱动_注册和注销
1、字符设备注册与注销的函数原型” /*字符设备注册的函数原型*/ static inline int register_chrdev(unsigned int major,\ const char *name, \ const struct file_operations *fops) /* major:主设备号,Limnux下每个设备都有一个设备号,设备号分…...

设计模式:软件工程的艺术
引言 设计模式是软件工程中一种解决常见问题的经验总结,是一套可复用的设计思想。它们提供了在特定情境下的解决方案,有助于构建可维护、灵活、可复用、可扩展的软件系统。设计模式是对软件设计中通用问题的抽象,提供了一种共享的语言和思维…...

试题 算法训练 数的潜能
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 将一个数N分为多个正整数之和,即Na1a2a3…ak,定义Ma1*a2*a3*…*ak为N的潜能。 给定N,…...
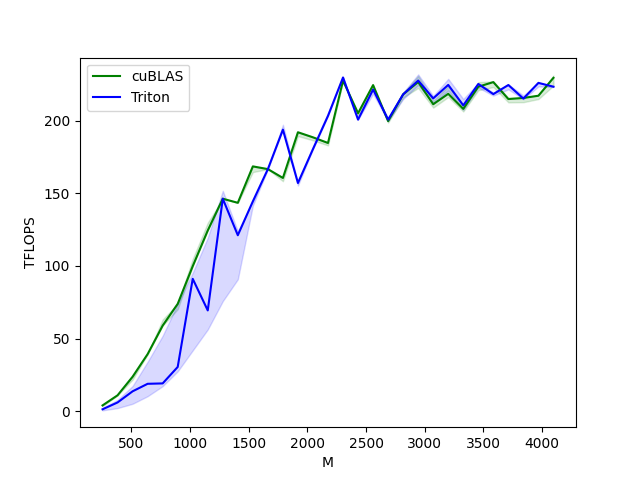
OpenAI Triton 入门教程
文章目录 Triton 简介背景Triton 与 CUDA 的关系 Triton 开发样例样例一:Triton vector addition 算子Triton kernel 实现kernel 函数封装函数调用性能测试 样例二:融合 Softmax 算子动机Triton kernel 实现kernel 封装单元测试性能测试 样例三ÿ…...

【flask+python】利用魔术方法,更优雅的封装model类
定义model # Time :2024-2024/2/27-14:49 # Email :514422868qq.com # Author :Justin # file :user.py # Software :01-fishbook from app.model.base import Base from sqlalchemy import Column, Integer, SmallInteger, String from werkzeug.security …...

Qt程序设计-报警灯自定义控件实例
本文讲解Qt报警灯自定义控件实例。 实现功能 设置边框和内部颜色。 设置是否闪烁点亮。 添加的报警灯类 #ifndef LIGHT_H #define LIGHT_H#include <QWidget> #include <QDebug> #include <QPainter> #include <QTimer>class Light : public QWid…...

Linux之定时任务02
一、什么是crond Linux 中 crond 就是定时任务,即根据 crond 指定的时间,由系统按指定的时间,周期性,自动触发的事件。 crond 服务在默认的情况下会每分钟检查系统中是否有定时任务,如果有且符合触发条件,…...

PHP堆栈+errLog定位
调用堆栈(Call Stack)是一个记录了程序在运行时所有活动子例程的栈结构。它以函数调用的方式描述了程序的执行流程和调用关系。 在PHP中,我们可以通过打印PHP调用堆栈来辅助调试和定位代码中的问题。本文将介绍如何在PHP中打印调用堆栈&…...
:Lookup Join、Array Expansion、Table Function)
【大数据】Flink SQL 语法篇(七):Lookup Join、Array Expansion、Table Function
《Flink SQL 语法篇》系列,共包含以下 10 篇文章: Flink SQL 语法篇(一):CREATEFlink SQL 语法篇(二):WITH、SELECT & WHERE、SELECT DISTINCTFlink SQL 语法篇(三&…...
【云原生】Spring Cloud Gateway的底层原理与实践方法探究
🎉🎉欢迎光临🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟特别推荐给大家我的最新专栏《Spring 狂野之旅:从入门到入魔》 🚀 本…...
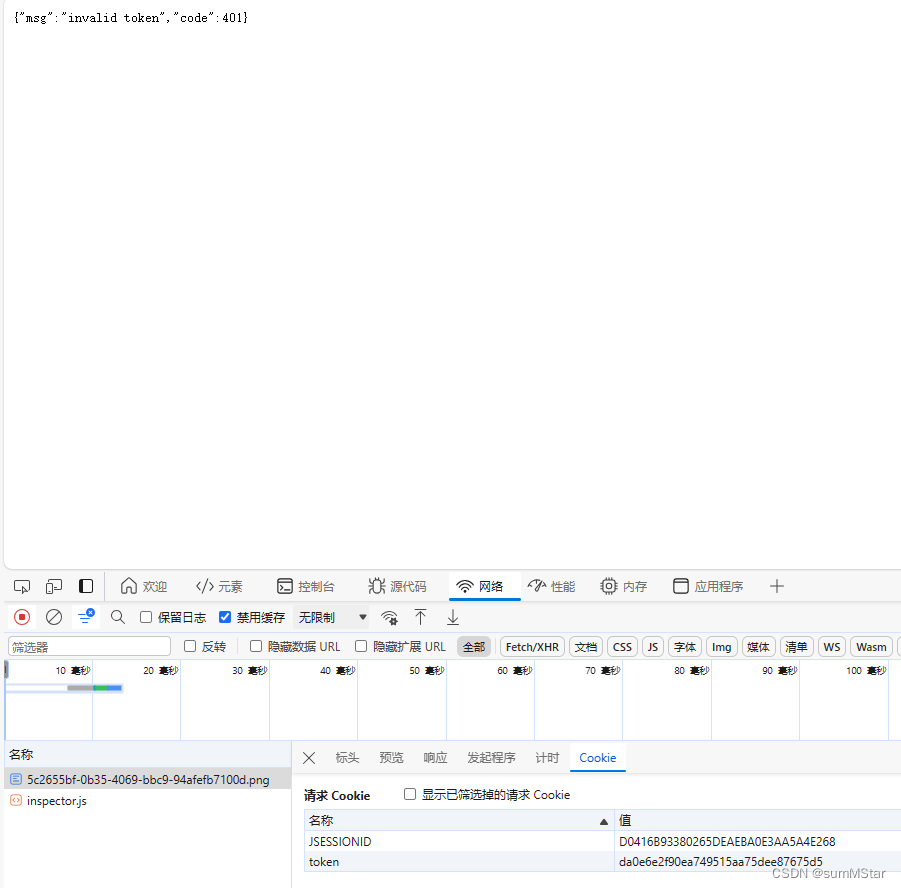
springboot 实现本地文件存储
springboot 实现本地文件存储 实现过程 上传文件保存文件(本地磁盘)返回文件HTTP访问服务器路径给前端,进行效果展示 存储 服务端接收上传的目的是提供文件的访问服务,对于SpringBoot而言,其对静态资源访问提供了很…...

Python进阶学习:Pandas--查看DataFrame中每一列的数据类型
Python进阶学习:Pandas–查看DataFrame中每一列的数据类型 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈 希…...
Groovy - 大数据共享搜索配置
数据共享搜索列中配置了搜索列,相应的数据共享接口中也需要支持根据配置的字段搜索,配置实体时,支持搜索的入参code必须是searchKeys,且接口应该是需要支持分页(入参必须是 current、pageSize)的。current …...

第三节:Vben Admin登录对接后端login接口
系列文章目录 第一节:Vben Admin介绍和初次运行 第二节:Vben Admin 登录逻辑梳理和对接后端准备 第三节:Vben Admin登录对接后端login接口 第四节:Vben Admin登录对接后端getUserInfo接口 第五节:Vben Admin权限-前端控制方式 文章目录 系列文章目录前言一、Flask项目介绍…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
