【FPGA】线性反馈移位寄存器(LFSR)的Verilog实现
什么是移位寄存器
移位寄存器:是指多个寄存器并排相连,前一个寄存器的输出作为下一个寄存器的输入,寄存器中存放的数据在每个时钟周期向左或向右移动一位。
下面的右移移位寄存器因为左侧没有有效输入,所以在第4个时钟周期,寄存器内就已经没有有效数据了。
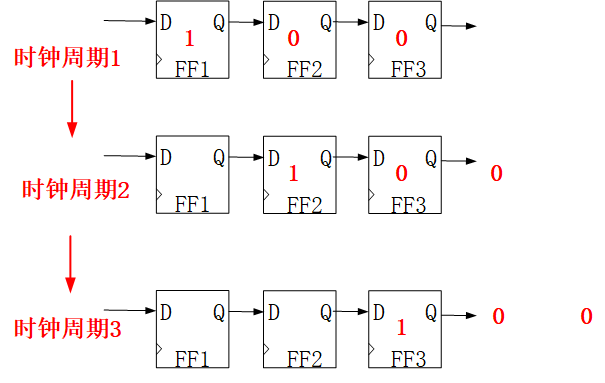
反馈移位寄存器:寄存器被移出的数据后又通过某种方式或函数重新连接到了移位寄存器的输入端,从而使得移位寄存器有不断的输出。
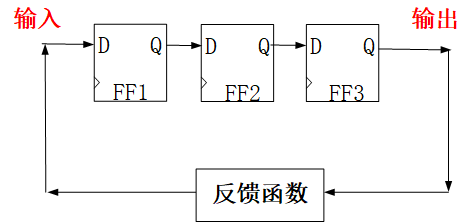
线性反馈移位寄存器(Linear-Feedback Shift Register,LFSR):当反馈移位寄存器的反馈函数为线性函数时,就称这个移位寄存器是反馈移位寄存器。LFSR所用的线性反馈函数一般为 异或 或者 同或。
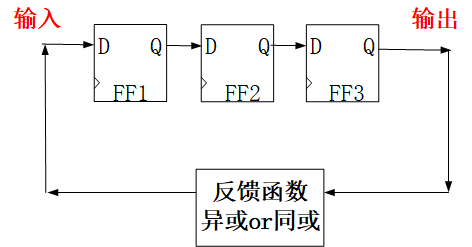
在每个时钟周期,LFSR的新的输入值会被反馈到内部各个寄存器的输入端,输入值中的一部分来源于LFSR的输出端,另一部分来源于LFSR各输出端进行异或运算得到。
什么是LFSR
LFSR的初始值被称为种子(Seed)。由异或门构成的LFSR的种子不能为全0,因为0与0异或永远为0,所以移位寄存器的输出永远都不会变化。同理,由同或门构成的LFSR的种子则不能为全1。
LFSR中的寄存器的个数被称为LFSR的级数。一个3级的LFSR最多同时存放3bit数据。一个n级的LFSR最多只有2^n - 1个状态(因为要排除全0状态 或 全1状态),比如3级的LFSR就只有7个状态。
LFSR的有些位参与反馈,有些位不参与反馈,其中参与的位被称为抽头。因为触发器编号从1开始,因此抽头的取值范围是1~(2^n-1)。
如果设计得当(与抽头有关),那么LFSR产生的状态可以是周期性的。只要选择合适的反馈函数便可使序列的周期达到最大值(2^n-1),周期达到最大值的序列称为m序列( m-sequence )。比如下面的LFSR(假设种子为111)会依次产生
111>110>100>001>010>101>011 这7个状态,然后又重新从111开始循环。
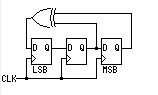
不同的级数如何选取正确的抽头?可以参考下面这个表,表内的抽头选取都是可以保证LFSR能运转到最多状态的。
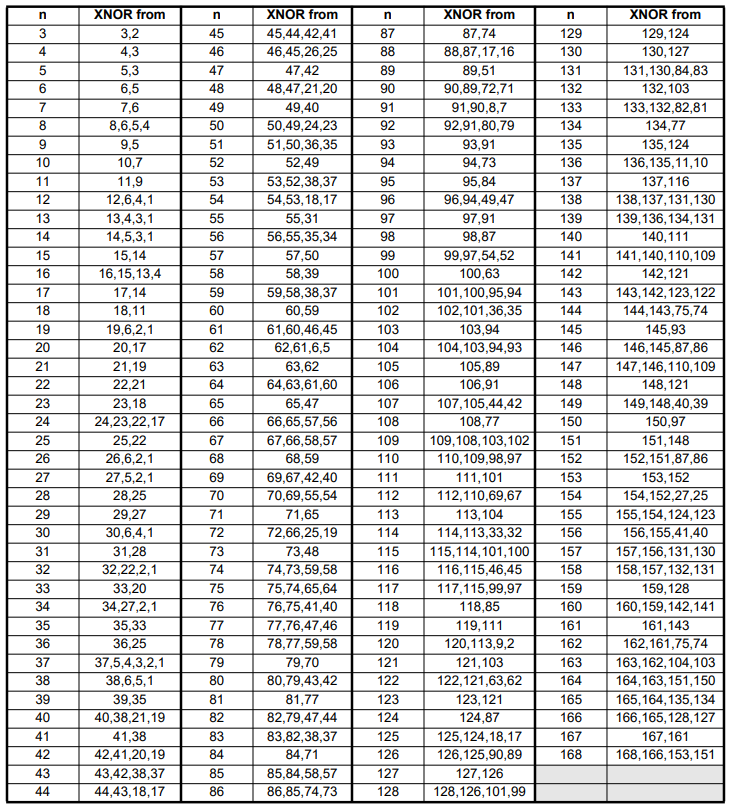
LFSR的两种分类
目前有两类常用的LFSR:斐波那契LFSR 和 伽罗瓦LFSR,下面分别就进行介绍。
斐波那契LFSR(Fibonacci LFSRs),又被称为多到一型LFSR,即多个触发器的输出通过反馈来驱动一个触发器的输入。下图是一个典型的斐波那契LFSR,反馈抽头为3和2。
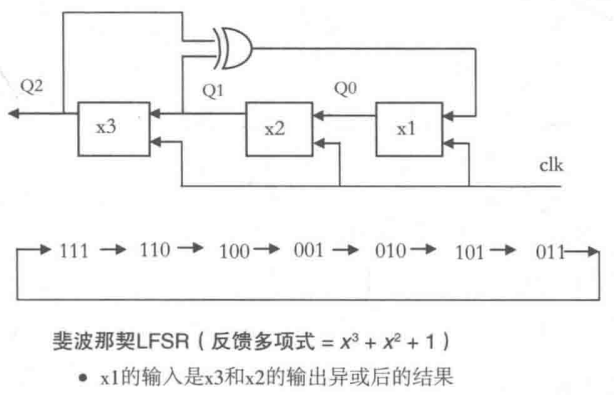
伽罗瓦LFSR(Fibonacci LFSRs),又被称为一到多型LFSR,即以个触发器的输出通过反馈来驱动多个触发器的输入。下图是一个典型的伽罗瓦LFSR,反馈抽头同样为3和2。这个伽罗瓦LFSR同样可以产生7级序列,但是序列的排序与斐波那契LFSR产生的序列是不同的。
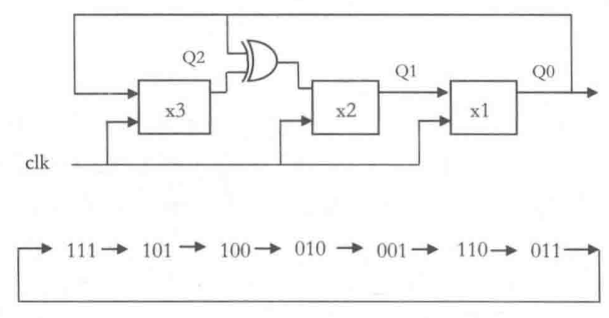
斐波那契LFSR和伽罗瓦LFSR有同样的功能,但是伽罗瓦LFSR的电路性能要由于斐波那契LFSR,因为它在两个触发器之间只使用了一个异或门(或者同或门)。
Verilog实现与仿真
下面用Verilog分别实现抽头为(8.6.5.4)的8级斐波那契LFSR和伽罗瓦LFSR,8级LFSR的状态数为2^8-1=255个。
.
这个网站LFSR自动工具有一个很好用的LFSR工具,可以自定义抽头、级数,反馈方式和LFSR种类,它可以自动生成Verilog代码和穷举所有的LFSR状态。
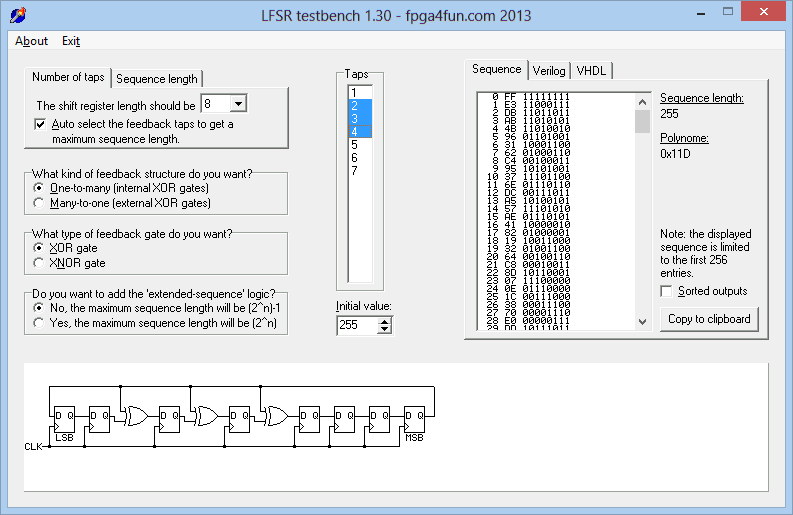
斐波那契LFSR
用同或门作为反馈函数生成抽头为(8.6.5.4)的8级斐波那契LFSR,Verilog代码如下:
//8级斐波那契LFSR(多到1型LFSR)设计
//同或门作为反馈函数,反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Fib(input clk,input rst, output reg [7:0] lfsr
);always @(posedge clk) beginif(rst)//同或门种子可以选取全0,同时FPGA复位后也会复位到0,比较方便lfsr <= 8'h0; else begin//抽头从1开始为8、6、5、4lfsr[0] <= ~(lfsr[3] ^ lfsr[4] ^ lfsr[5] ^ lfsr[7]);//低位移动到高位lfsr[7:1] <= lfsr[6:0];end
end
生成的LFSR示意图如下:
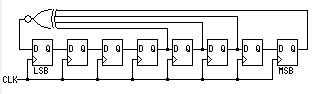
为了验证生成电路的正确性,需要编写TB文件进行验证。对于这种简单的模块(只有255个状态),最简单的验证办法就是穷举所有状态与正确状态进行对比即可。方法有几种:
方法1:手动对比
移位LFSR软件提供了所有正确的输出,所以我们只需要将正确的向量与仿真出来的波形结果一一对比即可,这种方法简单,但是效率较低,且容易出错。编写的TB文件如下:
`timescale 1ns/1ns
module tb_LFSR8_Fib();
//信号声明
reg clk;
reg rst;
reg [7:0] cnt; //记录状态个数,一共255个(没有全1状态)
wire [7:0] lfsr;//模块实例化
LFSR8_Fib inst_LFSR8_Fib(.clk (clk),.rst (rst), .lfsr (lfsr)
); //生成时钟信号
initial beginclk = 1'b1;forever #5 clk = ~clk;
end//生成复位信号
initial beginrst = 1'b1; //复位#45 rst = 1'b0; //取消复位
end//仿真过程
initial beginwait(cnt == 255); //所有状态都仿真结束#10 $stop; //关闭仿真
end//记录状态个数,每个有效时钟周期加1
always@(posedge clk)beginif(rst)cnt <= 8'd0;else begincnt <= cnt + 1'd1;end
endendmodule
仿真结果如下:

与正确向量一一对比即可,发现仿真结果无误。
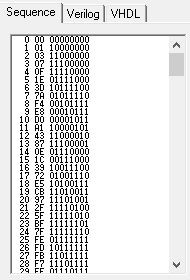
方法2:将仿真结果打印到Tcl窗口,然后复制到文件,再与正确向量对比。对比方式可以是手动对比,也可以是用插件自动进行对比。
这种方法只需要部分修改TB文件:
//记录状态个数,每个有效时钟周期加1
always@(posedge clk)beginif(rst)cnt <= 8'd0;else begincnt <= cnt + 1'd1;$display("%h",lfsr); //打印每一个状态到窗口end
end
然后Tcl窗口就打印出了仿真结果:
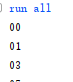
方法3:基本与方法2类似,只不过将将仿真结果直接打印到文件,再与正确向量对比。对比方式可以是手动对比,也可以是用插件自动进行对比。TB文件如下:
`timescale 1ns/1ns
module tb_LFSR8_Fib();
//信号声明
reg clk;
reg rst;
reg [7:0] cnt; //记录状态个数,一共255个(没有全1状态)
wire [7:0] lfsr;//定义文件句柄
integer handle_file_out; //模块实例化
LFSR8_Fib inst_LFSR8_Fib(.clk (clk),.rst (rst), .lfsr (lfsr)
); //生成时钟信号
initial beginclk = 1'b1;forever #5 clk = ~clk;
end//生成复位信号
initial beginrst = 1'b1; //复位#45 rst = 1'b0; //取消复位
end//仿真过程
initial beginwait(cnt == 255); //所有状态都仿真结束#10 $fclose(handle_file_out); //关闭文件$stop; //关闭仿真
end//打开文件file_out,相对路径需要与TB文件在同一目录下
initial begin//handle_file_out = $fopen("file_out.txt","w");//相对路径handle_file_out = $fopen("G:/file_out.txt","w");//绝对路径
end//记录状态个数,每个有效时钟周期加1
always@(posedge clk)beginif(rst)cnt <= 8'd0;else begincnt <= cnt + 1'd1;//$display("%h",lfsr); //打印每一个状态到窗口//打印每一个状态到文件$fdisplay(handle_file_out,"%h",lfsr); end
endendmodule
打开file_out文件,可以看到数据都已经被保存好了:

方法4:在TB文件中读取正确向量并自动与仿真结果一一对比,若对比有误则输出某个标志信号。TB文件如下:
`timescale 1ns/1ns
module tb_LFSR8_Fib();
//信号声明
reg clk;
reg rst;
wire [7:0] lfsr;reg [7:0] cnt; //记录状态个数,一共255个(没有全1状态)
reg [7:0] lfsr_gold [0:254]; //构建一个数组来存储正确向量,位宽为8,个数为255个
reg flag; //错误标志,1表示对比错误;0表示对比正确
reg [7:0] cnt_error; //错误计数器//模块实例化
LFSR8_Fib inst_LFSR8_Fib(.clk (clk),.rst (rst), .lfsr (lfsr)
); //生成时钟信号
initial beginclk = 1'b1;forever #5 clk = ~clk;
end//生成复位信号
initial beginrst = 1'b1; //复位#45 rst = 1'b0; //取消复位
end//读取正确向量
initial begin$readmemh("G:/file_in.txt",lfsr_gold); //绝对路径
end//仿真过程
initial beginwait(cnt == 255); //所有状态都仿真结束if (cnt_error == 0)//打印仿真成功信息$display("simulation succeed!");else//打印仿真错误信号$display("simulation failed,there is %d errors!",cnt_error);#10 $stop; //关闭仿真
end//记录状态个数,每个有效时钟周期加1
always@(posedge clk)beginif(rst)begincnt <= 8'd0;flag <= 1'b0;cnt_error <= 8'd0;end else begincnt <= cnt + 1'd1;if(lfsr_gold[cnt] != lfsr)begin //如果对比有误//$display("cnt=%d is wrong",cnt); //打印错误的地方flag <= 1'b1; //拉高错误标志cnt_error <= cnt_error + 1; //错误计数器加1endelse beginflag <= 1'b0;cnt_error <= cnt_error;end end
endendmodule
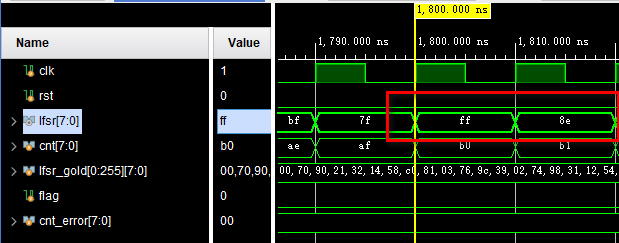
为了对比仿真结果,我故意把正确向量的第2个数据改成错误数据,仿真结果如下:
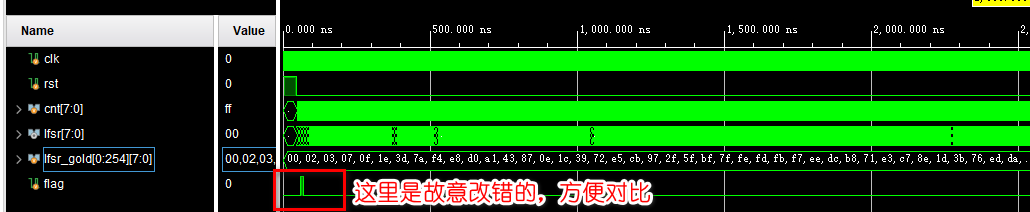
Tcl窗口也打印了错误:
把正确向量的错误修正后再仿真,仿真无误,打印的信息如下:

这种方式可以自动对比正确向量与仿真结果,大大提高了效率。
伽罗瓦LFSR
用同或门作为反馈函数生成抽头为(8.6.5.4)的8级伽罗瓦LFSR,Verilog代码如下:
//8级伽罗瓦LFSR(1到多型LFSR)设计
//同或门作为反馈函数,反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Gal(input clk,input rst, output reg [7:0] lfsr
);wire feedback;;assign feedback = lfsr[7];always @(posedge clk)beginif(rst)//同或门种子可以选取全0,同时FPGA复位后也会复位到0,比较方便lfsr <= 8'h0;else begin//抽头从1开始为8、6、5、4lfsr[0] <= feedback;lfsr[1] <= lfsr[0];lfsr[2] <= lfsr[1];lfsr[3] <= lfsr[2];lfsr[4] <= lfsr[3] ~^ feedback;lfsr[5] <= lfsr[4] ~^ feedback;lfsr[6] <= lfsr[5] ~^ feedback; lfsr[7] <= lfsr[6];end
endendmodule
电路示意图如下:
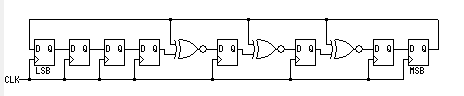
仿真脚本依然用上面的即可,这里就不啰嗦了。
禁止状态的处理
用同或门作为反馈函数的LFSR是禁止使用全1状态的,因为全1的同或还是1,会导致移位寄存器一直处于全1状态出不来。这是的n级的LFSR只有2^n - 1 个状态,比一般的计数器状态少1个。如果需要完善这种禁止状态的处理,可以增加一部分电路来改变。
斐波那契LFSR可以增加一个判断寄存器是否为全1的电路,并将其输出连接到同或门,示意图如下:
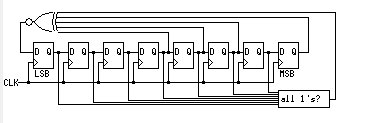
如果不为全1状态,则全1判断电路输出为0,0异或任何数都等于该数本身,即不会对原有电路造成影响。如果为全1状态,则全1判断电路输出为1,此时同或门的输出为0,所以下一个状态的最低位即为0,也就是说跳出了全1状态。
这部分的Verilog代码如下:
//8级斐波那契LFSR(多到1型LFSR)设计
//同或门作为反馈函数,反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Fib(input clk,input rst, output reg [7:0] lfsr
);always @(posedge clk) beginif(rst)//同或门种子可以选取全0,同时FPGA复位后也会复位到0,比较方便lfsr <= 8'h0; else begin//抽头从1开始为8、6、5、4;增加全1状态的跳出lfsr[0] <= ~(lfsr[3] ^ lfsr[4] ^ lfsr[5] ^ lfsr[7] ^ (lfsr[6:0]==7'b1111111));//低位移动到高位lfsr[7:1] <= lfsr[6:0];end
endendmodule
仿真也没问题,能从全1状态跳出:
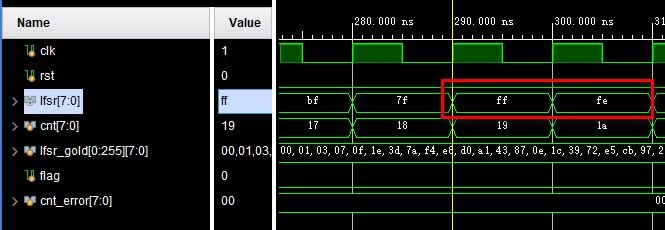
同理,伽罗瓦LFSR也可以增加一个判断寄存器是否为全1的电路,并将其输出连接到同或门,示意图如下:
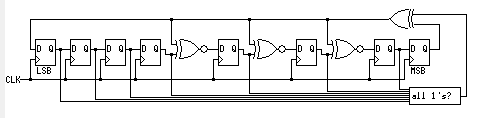
如果不为全1状态,则全1判断电路输出为0,0异或任何数都等于该数本身,即不会对原有电路造成影响。如果为全1状态,则全1判断电路输出为1,此时异或门的输出为0,所以下一个状态的抽头位全变为0,也就是说跳出了全1状态。
这部分的Verilog代码如下:
//8级伽罗瓦LFSR(1到多型LFSR)设计
//同或门作为反馈函数,反馈多项式为 f(x)=x^8 + x^6 + x^5 + x^4 + 1
module LFSR8_Gal(input clk,input rst, output reg [7:0] lfsr
);wire feedback;;//增加全1状态的跳出
assign feedback = lfsr[7] ^ (lfsr[6:0]==7'b1111111);;always @(posedge clk)beginif(rst)//同或门种子可以选取全0,同时FPGA复位后也会复位到0,比较方便lfsr <= 8'h0;else begin//抽头从1开始为8、6、5、4lfsr[0] <= feedback;lfsr[1] <= lfsr[0];lfsr[2] <= lfsr[1];lfsr[3] <= lfsr[2];lfsr[4] <= lfsr[3] ~^ feedback;lfsr[5] <= lfsr[4] ~^ feedback;lfsr[6] <= lfsr[5] ~^ feedback; lfsr[7] <= lfsr[6];end
endendmodule
仿真也没问题,能从全1状态跳出:
- 📣您有任何问题,都可以在评论区和我交流📃!
- 📣本文由 孤独的单刀 原创,首发于CSDN平台🐵,博客主页:wuzhikai.blog.csdn.net
- 📣您的支持是我持续创作的最大动力!如果本文对您有帮助,还请多多点赞👍、评论💬和收藏⭐!
相关文章:

【FPGA】线性反馈移位寄存器(LFSR)的Verilog实现
什么是移位寄存器 移位寄存器:是指多个寄存器并排相连,前一个寄存器的输出作为下一个寄存器的输入,寄存器中存放的数据在每个时钟周期向左或向右移动一位。 下面的右移移位寄存器因为左侧没有有效输入,所以在第4个时钟周期&…...

yolov8涨点技巧,添加SwinTransformer注意力机制,提升目标检测效果
目录 摘要 SwinTransformer原理 代码实现 YOLOv8详细添加步骤 ymal文件内容 one_swinTrans three_swinTrans 启动命令 完整代码分享 摘要 Swin Transformer通过引入创新的分层注意力机制展现了其架构的独特性,该机制通过将注意力区域划分为块并在这些块内执…...
k8s初始化错误
报错详情: you can check the kubelet logs for further clues by running: ‘journalctl -u kubelet’ Alternatively, there might be issues with your Kubernetes configuration files or maybe the necessary ports are not opened. Check the status of …...

adb命名大全
1. 获取内部版本号: adb shell getprop ro.build.display.innerver 2. 获取按键值: adb shell getevent 3. 获取apk信息: adb shell dumpsys package 包名 ->info.txt 4. 获取应用包名:adb shell dumpsys window windows | gre…...
携手共赴难)
计算机发展史 (5)携手共赴难
就在痛苦艰难的时刻,孤独苦闷的巴贝奇意外地收到一封来信,写信人不仅 对他表示理解而且还希望与他共同工作。娟秀字体的签名,表明了她不凡的身份 ──伯爵夫人。 接到信函后不久,巴贝奇实验室门口走进来一位年轻的女士。她身披素雅…...
一键搞定简历设计!电子版简历制作指南3步走!
如今,随着无纸化办公趋势的流行,电子简历逐渐取代了纸质简历,成为我们最常用的简历设计格式。 然而,从纸质简历到电子简历后,对于非平面设计领域的学生来说,简历设计的难度可能再次超出了我们的能力范围。…...
tcpdump 常用用法
简要记录下tcpdump用法 监控某个ip上的某个端口的流量 tcpdump -i enp0s25 tcp port 5432 -nn -S 各个参数作用 -i enp0s25 指定抓包的网卡是enp0s25 -nn 显示ip地址和数字端口 ,如果只 -n 则显示ip,但是端口为services文件中的服务名 如果一个…...
Opencv实战(5)平滑处理与常见函数
平滑处理 Opencv实战: Opencv(1)读取与图像操作 Opencv(2)绘图与图像操作 Opencv(3)详解霍夫变换 Opencv(4)详解轮廓 文章目录 平滑处理1.均值滤波2.方框滤波3.高斯滤波4.中值滤波5.双边滤波 常见函数(1).createTrackbar()(2).SetMouseCallback() 图像的平滑处理是…...

音频PCM介绍与运用
音频PCM介绍与运用 什么是PCM PCM (Pulse Code Modulation) 是一种数字音频编码方式,将模拟声音信号转换为数字信号的过程。在 PCM 中,声音信号被采样并量化为离散的数值,以便于数字化处理和传输。 以下是 PCM 的主要特点: 采样…...

计算机专业大学四年应该如何规划(Java方向)
计算机专业的学生,如何在大学四年内提高自己的竞争力,毕业之后直接进大厂工作? 以下将从大学四年计算机专业的学习规划、课程设置、能力提升、参考书籍等方面,为同学们提供一些建议和指导。 大一: 主攻技能学习并且达…...

算法D27|回溯算法4| 93.复原IP地址 78.子集 90.子集II
93.复原IP地址 本期本来是很有难度的,不过 大家做完 分割回文串 之后,本题就容易很多了 题目链接/文章讲解:代码随想录 视频讲解:回溯算法如何分割字符串并判断是合法IP?| LeetCode:93.复原IP地址_哔哩哔…...

C++实现XOR加解器
#include <Windows.h> #include <iostream> #include <fstream> #include <string>// 加解密函数,使用XOR运算 void XORCrypt(char* data, int size, const std::string& key) {int keyLength key.length();for (int i 0; i < siz…...

Kubernetes的Sevice管理
服务原理: 所有服务都是根据这个服务衍生或者变化出来,根服务---- 服务感知后端靠标签 slelector 标签选择器 kubectl label pods web1 appweb kubectl cluter-info dump | grep -i service-cluster-ip-range 服务ip取值范围 Service 管理: 创建服务: --- kind: Serv…...
C# 高阶语法 —— Winfrom链接SQL数据库的存储过程
存储过程在应用程序端的使用的优点 1 如果sql语句直接写在客户端,以一个字符串的形式体现的,提示不友好,会导致效率降低 2 sql语句写在客户端,可以利用sql注入进行攻击,为了安全性,可以把sql封装在…...
vue3+vite+ts配置多个代理并解决报404问题
之前配置接口代理总是报404,明明接口地址是对的但还是报是因数写法不对;用了vue2中的写法 pathRewrite改为rewrite 根路径下创建env文件根据自己需要名命 .env.development文件内容 # just a flag ENVdevelopment# static前缀 VITE_APP_PUBLIC_PREFIX"" # 基础模块…...

开创未来:探索OpenAI首个AI视频模型Sora的前沿技术与影响
Sora - 探索AI视频模型的无限可能 随着人工智能技术的飞速发展,AI视频模型已成为科技领域的新热点。而在这个浪潮中,OpenAI推出的首个AI视频模型Sora,以其卓越的性能和前瞻性的技术,引领着AI视频领域的创新发展。让我们将一起探讨…...
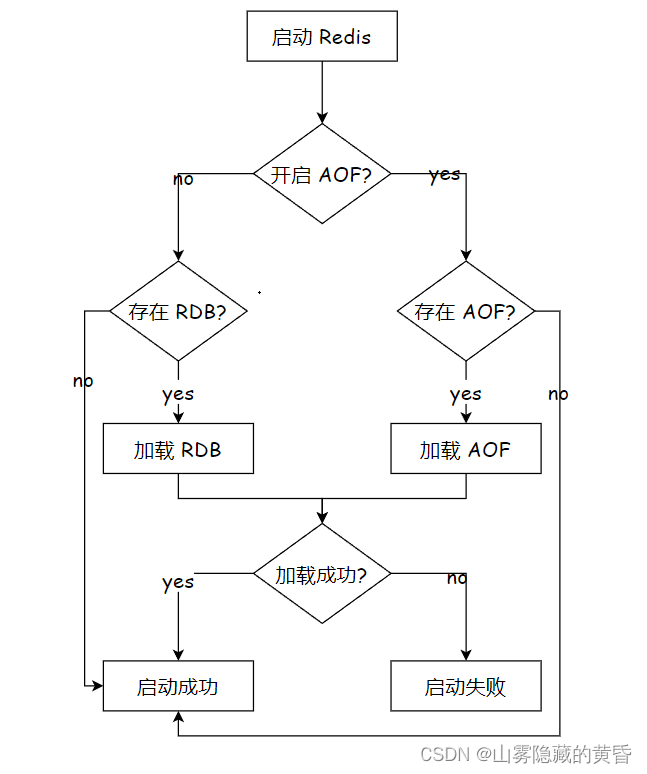
Redis---持久化
Redis是内存数据库,是把数据存储在内存中的,但是内存中的数据不是持久的,如果想要做到持久,那么就需要让redis将数据存储到硬盘上。 Redis持久化有两种策略: RDB > Redis DataBase RDB机制采取的是定期备份AOF …...
从 Flask 切到 FastAPI 后,起飞了!
我这几天上手体验 FastAPI,感受到这个框架易用和方便。之前也使用过 Python 中的 Django 和 Flask 作为项目的框架。Django 说实话上手也方便,但是学习起来有点重量级框架的感觉,FastAPI 带给我的直观体验还是很轻便的,本文就会着…...

状态码转文字!!!(表格数字转文字)
1、应用场景:在我们的数据库表中经常会有status这个字段,这个字段经常表示此类商品的状态,例如:0->删除,1->上架,0->下架,等等。 2、我们返回给前端数据时,如果在页面显示0…...

Pytorch 复习总结 4
Pytorch 复习总结,仅供笔者使用,参考教材: 《动手学深度学习》Stanford University: Practical Machine Learning 本文主要内容为:Pytorch 深度学习计算。 本文先介绍了深度学习中自定义层和块的方法,然后介绍了一些…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
