字符串模式匹配,经典KMP算法你还不会?我可不允许你不会!
文章目录
- 重点
- 1. 简单模式匹配算法
- 2. 部分匹配值PM的算法(Move = j-1 + PM[j-1])
- 3. 部分匹配值PM的两次改进(Move = j-next[j])
- 4. 快速得到next数组
- 5. KMP匹配算法
重点
童鞋们看网上讲解的时候一定要分清楚序列是从0开始还是从1开始,有些博主就是纯纯的转载文章,没有任何修改,把一篇错误的文章转来转去,误导了同学们。
所以我在这里提醒同学们一定要注意序列下标从什么开始的。
我的算法是根据王道考研总结出来的,并且主串、模式、next的下标都是从1开始的
1. 简单模式匹配算法

int search(String txt, String part){for(int i=0; i<txt.length-part.length; ++i){for(int j=0; j<M; j++){if(part[j] != txt[i+j]) break;}if(j == M) return i;}return -1;
}
2. 部分匹配值PM的算法(Move = j-1 + PM[j-1])
1. 部分匹配值PM
模式(a b c a c)
‘a’的前缀为空,后缀为空,两者交集为空;
‘ab’的前缀为{a},后缀为{b},两者交集为空;
‘abc’的前缀为{a,ab},后缀为{bc,c},两者交集为空;
'abca’的前缀为{a,ab,abc},后缀{bca,ca,a},两者交集为{a};
‘abcac’的前缀为{a,ab,abc,abca},后缀{bcac,cac,ac,c},两者交集为空
2. 利用上述得到的部分匹配值PM完成匹配
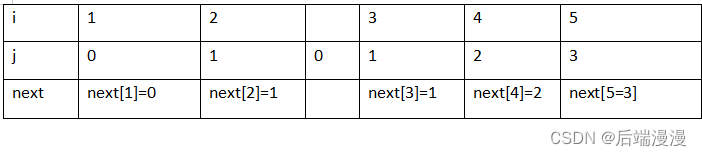
【第一趟匹配过程】
发现a与c不匹配,前两个字符是匹配的,查表可知,最后一个匹配字符b对应的部分匹配值为0,因此:移动位数=已匹配的字符数 - 对应的部分匹配值=2-0=2,所以将子串向后移动2位。j=1+PM
【第二趟匹配过程】
发现b与c不匹配,前四个字符是匹配的,查表可知,最后一个匹配字符a对应的部分匹配值为1,因此:移动位数=已匹配的字符数 - 对应的部分匹配值=4-1=3,所以将子串向后移动3位。j=1+PM
【第三趟匹配过程】
成功
3. 具体实例

3. 部分匹配值PM的两次改进(Move = j-next[j])
已知:右移位数=已匹配的字符数 - 对应的部分匹配值,即为Move=(j-1)- PM[j-1];
使用部分匹配值时,每当匹配失败,就去找它前一个元素的部分匹配值,这样使用起来有些不方便,所以将PM表右移一位,这样哪个元素匹配失败,直接看它自己的部分匹配值即可。

有时候为了让公式变得更加简洁,可以将next数组整体+1;

于是next数组就出来了
4. 快速得到next数组
1. 手动画图
已知串 S= "babab ", 求 Next 数值序列(模式匹配)
- 首先第一位0,第二位1。这个是固定的。
- 第三位,字符串是“bab”,这时候“bab”的前缀有b,ba;后缀有ab,b,可以看出前后缀相等的最长的字符串只有b,因为b的长度是1,所以这里第三位的next值就是1。
- 第四位,字符串是“baba”,前缀是b,ba,bab;后缀是aba,ba,a。这里可以看出前后缀相等的最长的字符串是ba,长度是2,因此第四位的next值是2。
- 第五位,字符串是“babab”,前缀是b,ba,bab,baba;后缀是abab,bab,ab,b。这里可以看出前后缀相等的最长的字符串是bab,长度是3,因此第五位的next值是3.
- 因此综合起来next值就是0 1 1 2 3
2. 代码实现next数组
void get_next(String T,int next[]){int i=1,j=0;next[1]=0;while(i<T.length){if(j==0||T.ch[i]==T.ch[j]){++i,++j;next[i]=j;}else j=next[j];}
}
5. KMP匹配算法
int Index(SString S,SString T,int next[]){int i=1,j=1;while(i<=S.length&&j<=T.length){//相同的话就一直匹配 if(j==0||S.ch[i]==T.ch[j]){ ++i; ++j; }//不同的话就回溯else{ j=next[j];}}//找到了,(i-1)-(T.length-1)=i-T.lengthif(j>T.length) return i-T.length; //没找到else return 0;
}
相关文章:

字符串模式匹配,经典KMP算法你还不会?我可不允许你不会!
文章目录重点1. 简单模式匹配算法2. 部分匹配值PM的算法(Move j-1 PM[j-1])3. 部分匹配值PM的两次改进(Move j-next[j])4. 快速得到next数组5. KMP匹配算法重点 童鞋们看网上讲解的时候一定要分清楚序列是从0开始还是从1开始&…...
)
C++操作redis(实现连接池、分布式锁)
文章目录Redis连接池编译项目整体架构使用分布式锁总结Redis连接池 封装hiredis的一些基本操作,redishelper类提供包含连接,放回,存取键,push,pop,执行redis语句和执行lua脚本的函数,连接池是类…...
硬件基础专题-01电阻篇
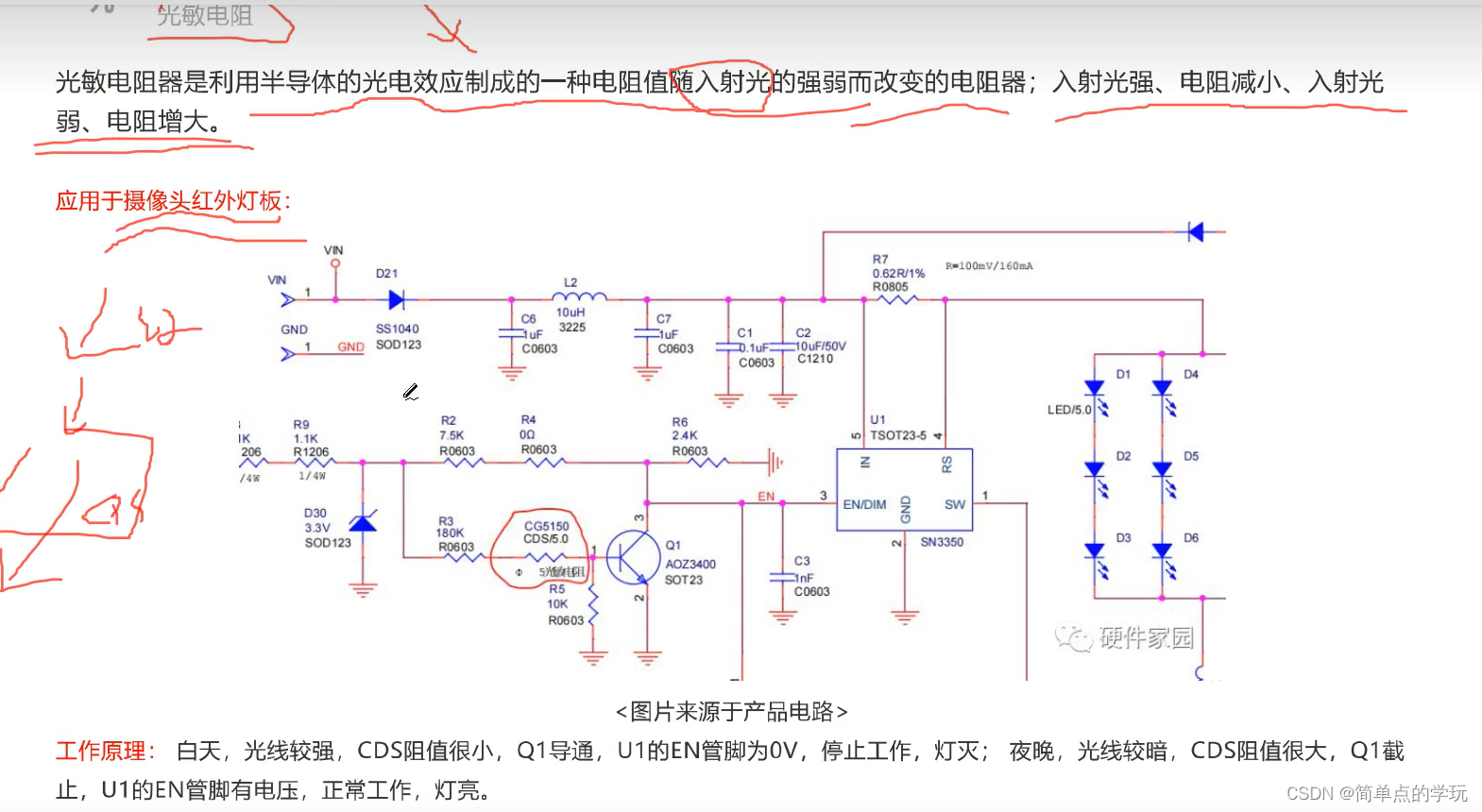
目录 课程链接 学习目的 电阻 电阻理论讲解 电阻定义 欧姆定律 电阻单位换算 电阻选型考虑 安装方式 常见电阻值 各种贴片电阻的读取方式 确定电阻值的方法 电阻数据手册 电阻测量 电阻的产品应用 零欧姆电阻 热敏电阻 光敏电阻 课程链接 视频专辑 - 硬件…...

【JAVA程序设计】(C00112)基于Springboot+Thymeleaf的在线购物商城——有文档
基于SpringbootThymeleaf的在线购物商城——有文档项目简介项目获取开发环境项目技术运行截图运行视频项目简介 基于Springbootthymeleaf框架的在线购物商城系统,本系统共分为二个角色:管理员和用户 管理员角色包含以下功能: 商品管理、商品…...
shell基础(5)算数计算:运算语法、自增自减
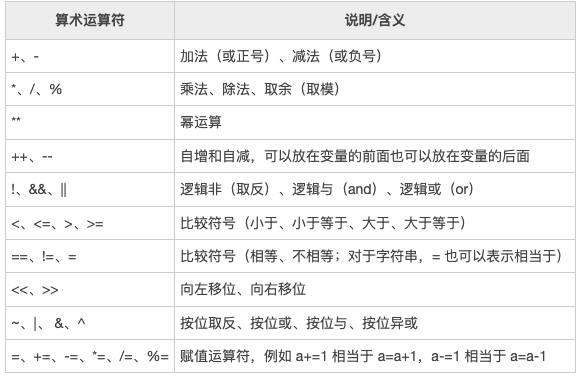
文章目录1. shell算数运算的特点2. 运算符一览3. 运算语法3.1 整形运算3.2. 小数运算 ing4. 自增自减4.1. a与a4.2. 自加1. shell算数运算的特点 Shell 和其它编程语言不同,Shell 不能直接进行算数运算,必须使用数学计算命令。Shell只支持整数运算&#…...

virtio设备input节点
注册virtio_input_node节点,节点类型为VLIB_NODE_TYPE_INPUT。 VLIB_REGISTER_NODE (virtio_input_node) {.name "virtio-input",.sibling_of "device-input",.format_trace format_virtio_input_trace,.flags VLIB_NODE_FLAG_TRACE_SUPP…...
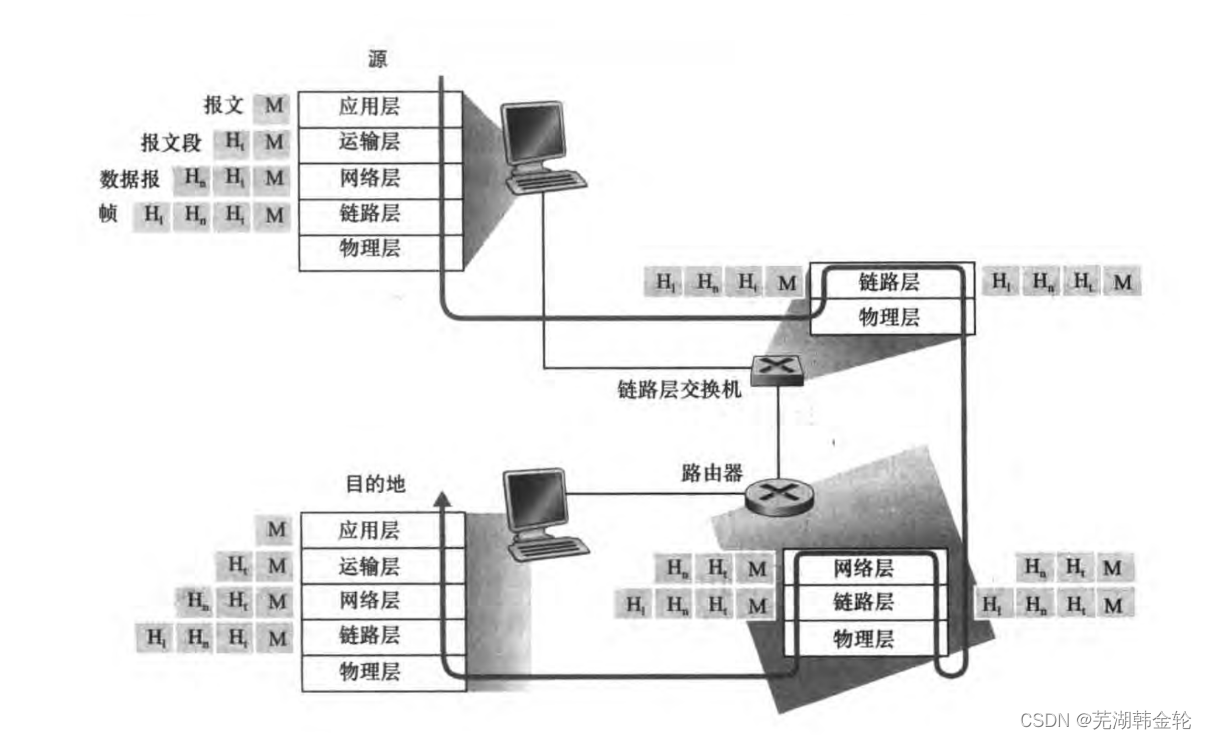
《计算机网络:自顶向下方法》学习笔记——第一章:计算机网络和因特网
计网 第一章 计算机网络和因特网 1.1 什么是因特网 回答这个问题有两种方式 其一,我们能够描述因特网的具体构成,即构成因特网的基本硬件和软件组件;其二,我们能够根据为分布式应用提供服务的联网基础设施来描述因特网。 1.1.…...

PDF 解析格式化输出 API 数据接口
PDF 解析格式化输出 API 数据接口 支持输出 TEXT HTML XML TAG,多种格式输出,超精准识别率。 1. 产品功能 通用的识别接口, 支持标准 PDF 文件解析;多种格式输出,支持 TEXT HTML XML TAG;HTML 包含完美排…...

RL笔记:基于策略迭代求CliffWaking-v0最优解(python实现)
目录 1. 概要 2. 实现 3. 运行结果 1. 概要 CliffWalking-v0是gym库中的一个例子[1],是从Sutton-RLbook-2020的Example6.6改编而来。不过本文不是关于gym中的CliffWalking-v0如何玩的,而是关于基于策略迭代求该问题最优解的实现例。 CliffWalking-v0的…...

350. 两个数组的交集 II
两个数组的交集 II 给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结…...
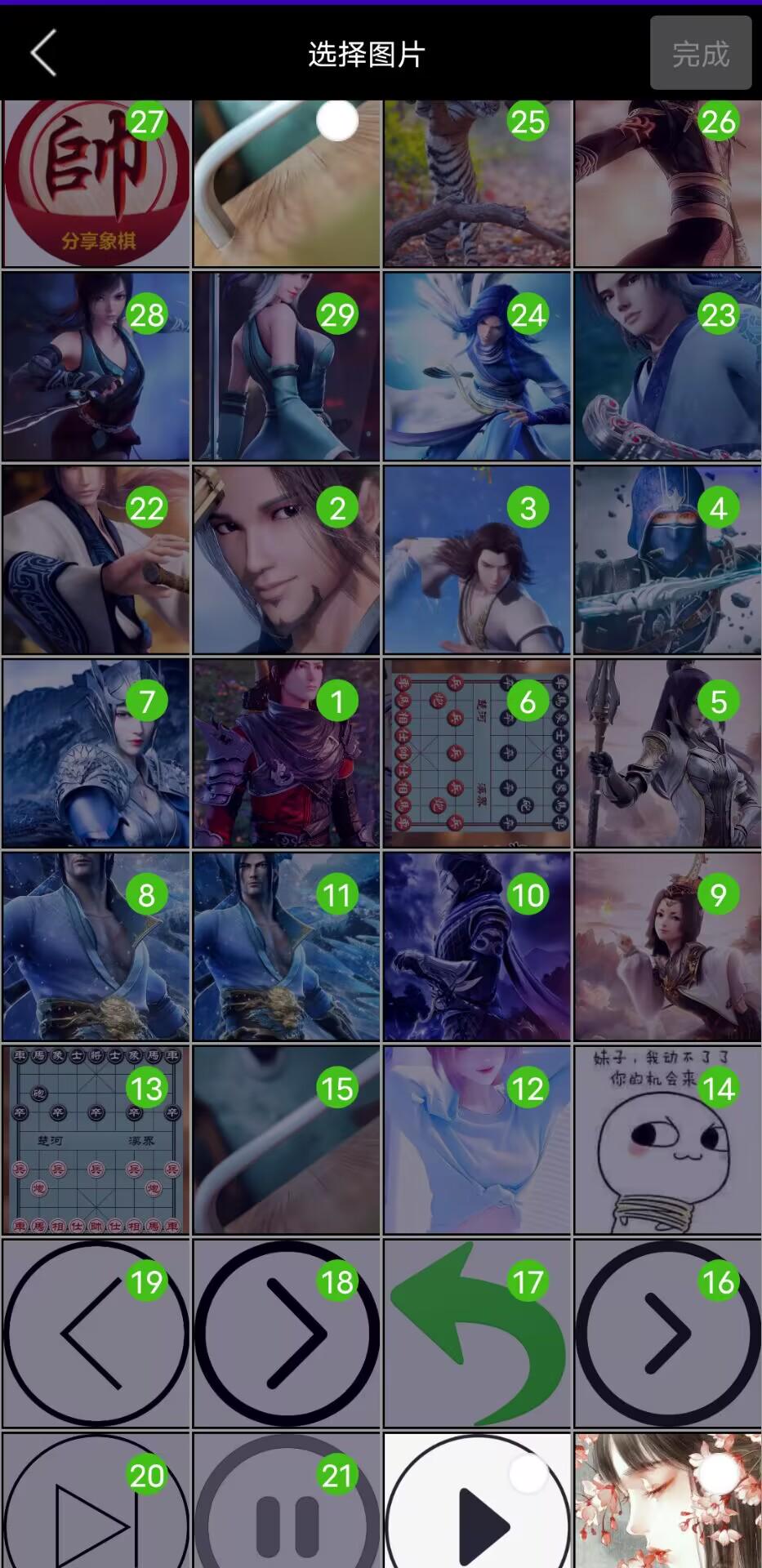
Android仿微信选择图片
效果展示首先先添加用到的权限<uses-permission android:name"android.permission.INTERNET" /><!--获取手机存储卡权限--><uses-permission android:name"android.permission.READ_EXTERNAL_STORAGE"/><uses-permission android:nam…...

python+嵌入式——串口通信篇(收发解包)
目录前言安装pyserialpyserial大致概括整体流程硬件连接例子(简单版)详细使用serial初始化参数发包收包收包检查包并解包python struct模块结语前言 这几年,自己也做了一些嵌入式机器人。在整个开发的过程中,调通信通常会花费一段比较长的时间ÿ…...
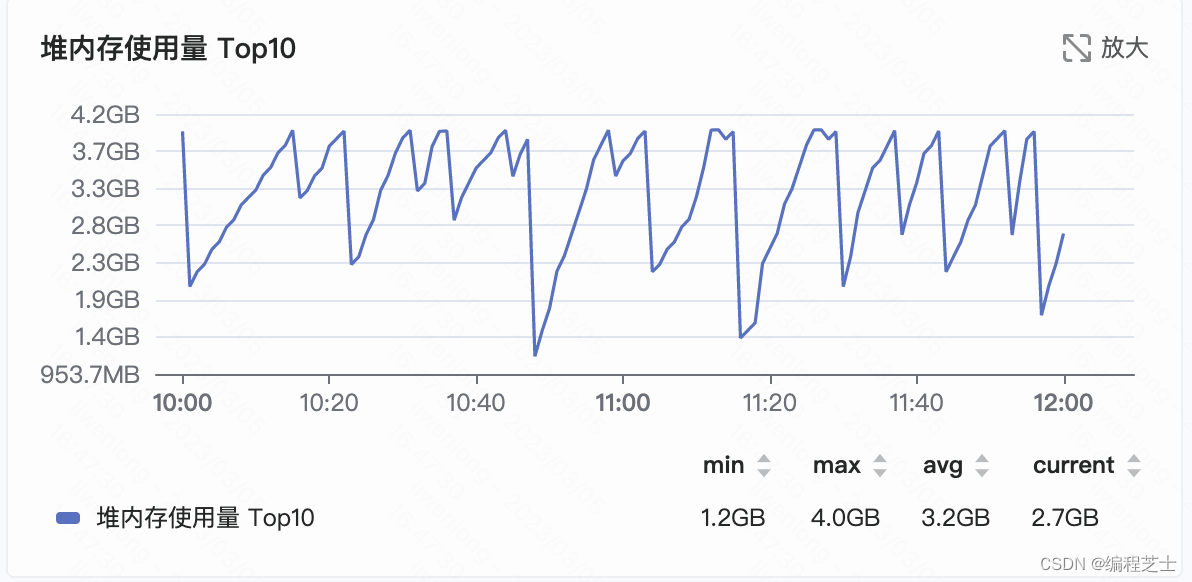
剖析G1 垃圾回收器
简单回顾 在Java当中,程序员在编写代码的时候只需要创建对象,从来不需要考虑将对象进行释放,这是因为Java中对象的垃圾回收全部由JVM替你完成了(所有的岁月静好都不过是有人替你负重前行)。 而JVM的垃圾回收由垃圾回收器来负责,在…...
如何打造一款专属于自己的高逼格电脑桌面
作为一名电脑重度使用者,你是否拥有一款属于你自己的高逼格电脑桌面呢?你是不是也像大多数同学一样,会把所有的内容全部都堆积到电脑桌面,不仅找东西困难,由于桌面内容太多还会导致C盘空间不足,影响电脑的反…...

【C++】string的使用及其模拟实现
文章目录1. STL的介绍1.1 STL的六大组件1.2 STL的版本1.3 STL的缺陷2. string的使用2.1 为什么要学习string类?2.2 常见构造2.3 Iterator迭代器2.4 Capacity2.5 Modifiers2.6 String operations3. string的模拟实现3.1 构造函数3.2 拷贝构造函数3.3 赋值运算符重载和…...

怀念在青鸟的日子
时间过的可真快,一转眼来到了2023年!我初中上完就没有在念,下了学门步入社会,那时的我一片迷茫,不知道该去干什 么,父母说要不去学挖掘机、理发、修车...我思考再三,一个都没有我喜欢的…...

学习记录---Python内置类型
文章目录字符串split()列表常见操作列表相减字典创建普通创建eval(s)添加或更新元素d[t] 1d.update({c: 3}){**d1, **d2} **字典解包装运算符删除元素 d.pop(c)属性d.items()d.keys()d.values()访问元素d[Name]d.get(score)遍历字典for key in dictfor key, values in dict.it…...
Python笔记 -- 列表
文章目录1、列表简介2、修改、添加、删除元素2.1、添加2.2、删除3、排序、倒序4、遍历列表5、创建数值列表6、列表切片7、列表复制8、元组1、列表简介 在Python中用方括号[]表示列表,用逗号隔开表示其元素 通过索引访问列表 names [aa,bb,cc,dd]print(names[0]) …...

谈谈UVM中的uvm_info打印
uvm_info宏的定义如下: define uvm_info(ID,MSG,VERBOSITY) \begin \if (uvm_report_enabled(VERBOSITY,UVM_INFO,ID)) \uvm_report_info (ID, MSG, VERBOSITY, uvm_file, uvm_line); \end 从这里可以看出uvm_info由两部分组成:uvm_report_enabled(VER…...
)
矩阵理论1 集合上的等价关系(equivalence relations on a set S)
定义 对于一个集合S, 如果集合E⊂SS\mathcal{E} \subset S\times SE⊂SS满足以下条件 自反性: 对于∀s∈S,都有(s,s)∈E\forall s\in S, 都有 (s, s) \in \mathcal{E}∀s∈S,都有(s,s)∈E对称性: (s,t)∈E⇔(t,s)∈E(s,t) \in \mathcal{E} \Leftrightarrow (t,s)\in \mathcal…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...