生物素-琥珀酰亚胺酯Biotin-NHS；CAS号：35013-72-0；可对溶液中的抗体，蛋白质和任何其他含伯胺的大分子进行简单有效的生物素标记。
结构式：
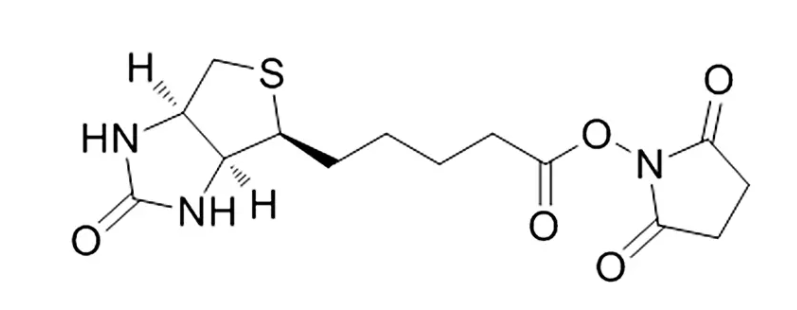
生物素-琥珀酰亚胺酯Biotin NHS CAS号：35013-72-0
英文名称：Biotin-NHS
中文名称：D-生物素 N-羟基琥珀酰亚胺酯；生物素－琥珀酰亚胺酯
CAS号：35013-72-0
密度：1.5±0.1 g/cm3
熔点：212-214 °C
分子式：C14H19N3O5S
分子量：341.383
外观性状：白色粉末
折射率：1.616
储存条件：密封、在 -20ºC下保存
溶剂：二甲基亚砜、二甲基甲酰胺
Biotin NHS是用于制备生物素化表面或多肽的氨基反应性生物素试剂，可与伯氨基（-NH2）有效结合，形成稳定、不可逆的酰胺键。
生物素-NHS试剂可对溶液中的抗体，蛋白质和任何其他含伯胺的大分子进行简单有效的生物素标记。
类似材料有：
Biotin-SS-Azide 生物素-二硫键-叠氮 CAS：1620523-64-9
Biotin-SS-NHS CAS：142439-92-7
Sulfo-NHS-SS-Biotin CAS：325143-98-4
Sulfo-NHS-Biotin CAS: 119616-38-5
Biotin-NHS CAS: 35013-72-0
相关文章：
生物素-琥珀酰亚胺酯Biotin-NHS；CAS号：35013-72-0；可对溶液中的抗体，蛋白质和任何其他含伯胺的大分子进行简单有效的生物素标记。
结构式： 生物素-琥珀酰亚胺酯Biotin NHS CAS号：35013-72-0 英文名称：Biotin-NHS 中文名称：D-生物素 N-羟基琥珀酰亚胺酯；生物素－琥珀酰亚胺酯 CAS号：35013-72-0 密度：1.50.1 …...
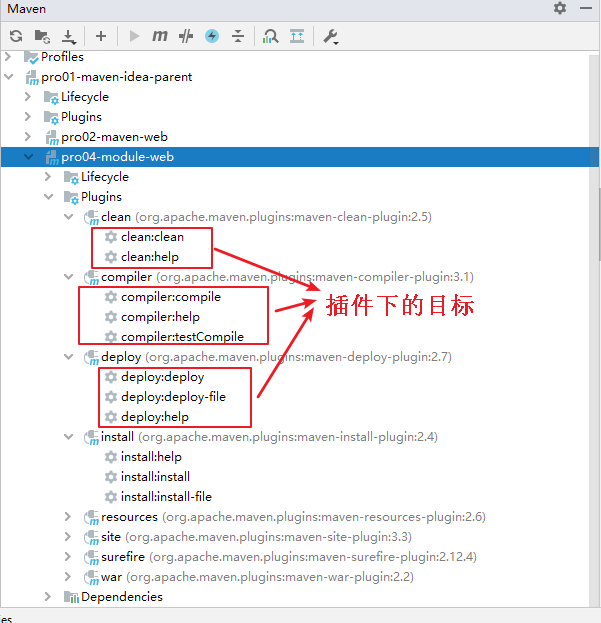
Maven_第五章 核心概念
目录第五章 其他核心概念1、生命周期①作用②三个生命周期③特点2、插件和目标①插件②目标3、仓库第五章 其他核心概念 1、生命周期 ①作用 为了让构建过程自动化完成，Maven 设定了三个生命周期，生命周期中的每一个环节对应构建过程中的一个操作。 …...
【深度学习】人脸识别工程化落地
文章目录前言1、facenet2、使用2.1.其它blog2.2 实践总结前言 老早以前就希望能写一篇关于人脸识别的工程化落地的案例，一年前做疲劳驾驶时使用的dlib插件，它封装好了，人脸检测、对齐、相似度计算三个部分,就是插件比较难装,但同时也少了很多…...
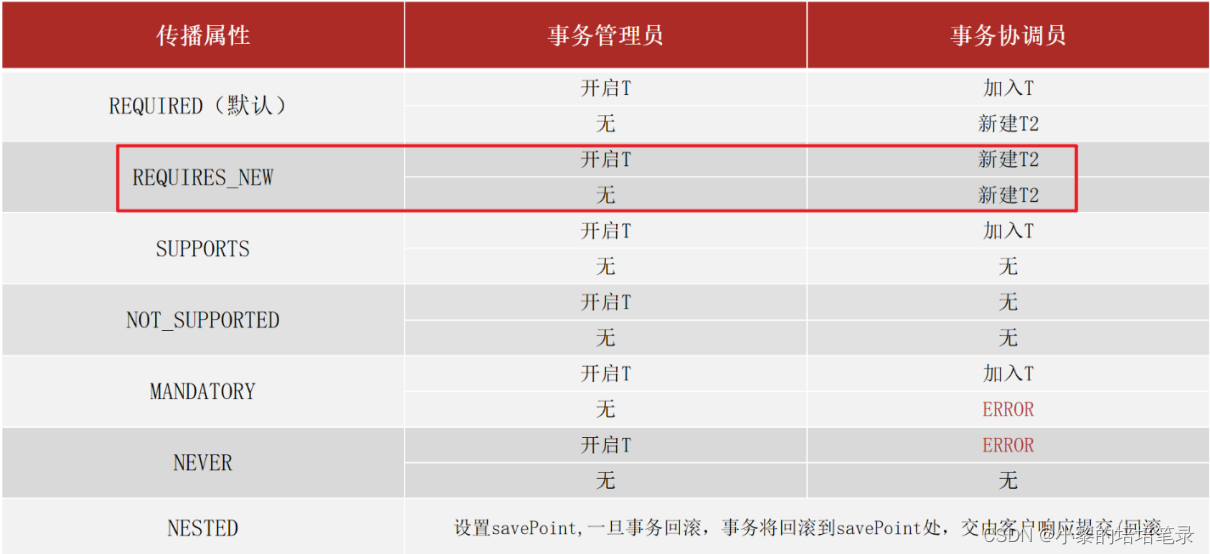
AOP面向切面编程思想。
目录 一、AOP工作流程 1、基本概念 2、AOP工作流程 二、AOP核心配置 1、AOP切入点表达式 2、AOP通知类型 三、AOP通知获取数据 1、获取参数 2、获取返回值 3、获取异常 四、AOP事务管理 1、Spring事务简介 2、Spring事务角色 3、事务属性 一、AOP工作流程 1、…...
实验7-变治技术及动态规划初步
目录 1.统计个数 2.数塔dp -A 3.Horspool算法 4.计数排序 5.找零问题1-最少硬币 1.统计个数 【问题描述】有n个数、每个元素取值在1到9之间，试统计每个数的个数 【输入形式】第一行，n的值；第二行...
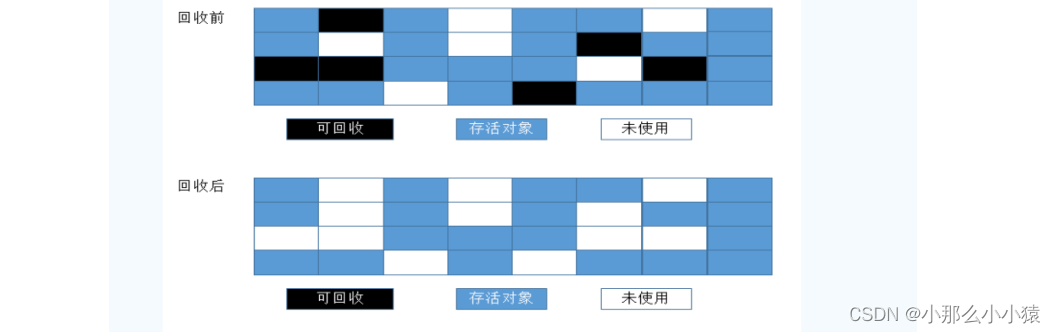
JVM垃圾回收机制GC理解
目录JVM垃圾回收分代收集如何识别垃圾引用计数法可达性分析法引用关系四种类型： 强、软、弱、虚强引用软引用 SoftReference弱引用 WeakReferenceWeakHashMap软引用与虚引用的使用场景虚引用与引用队列引用队列虚引用 PhantomReference垃圾回收算法引用计数复制 Cop…...
C++中的容器
1.1 线性容器1）std::array看到这个容器的时候肯定会出现这样的问题：为什么要引入 std::array 而不是直接使用 std::vector？已经有了传统数组，为什么要用 std::array?先回答第一个问题，与 std::vector 不同，…...
2023备战金三银四，Python自动化软件测试面试宝典合集（五）
接上篇八、抓包与网络协议8.1 抓包工具怎么用 我原来的公司对于抓包这块，在 App 的测试用得比较多。我们会使用 fiddler 抓取数据检查结果，定位问题，测试安全，制造弱网环境;如：抓取数据通过查看请求数据，请…...
SpringDI自动装配BeanSpring注解配置和Java配置类
依赖注入 上篇博客已经提到了DI注入方式的构造器注入，下面采用set方式进行注入 基于set方法注入 public class User {private String name;private Address address;private String[] books;private List<String> hobbys;private Map<String,String>…...
2月面经：真可惜...拿了小米的offer，字节却惨挂在三面
我是2月份参加字节跳动和华为的面试的，虽然我只拿下了小米的offer，但是我自己也满足了，想把经验分享出来，进而帮助更多跟我一样想进大厂的同行朋友们，希望大家可以拿到理想offer。 自我介绍 我是16年从南京工业大学毕…...
磐云PY-B8 网页注入
文章目录1.使用渗透机场景windows7中火狐浏览器访问服务器场景中的get.php，根据页面回显获取Flag并提交；2.使用渗透机场景windows7中火狐浏览器访问服务器场景中的post.php，根据页面回显获取Flag并提交；3.使用渗透机场景windows7中…...
多传感器融合定位十-基于滤波的融合方法Ⅰ其二
多传感器融合定位十-基于滤波的融合方法Ⅰ其二3. 滤波器基本原理3.1 状态估计模型3.2 贝叶斯滤波3.3 卡尔曼滤波(KF)推导3.4 扩展卡尔曼滤波(EKF)推导3.5 迭代扩展卡尔曼滤波(IEKF)推导4. 基于滤波器的融合4.1 状态方程4.2 观测方程4.3 构建滤波器4.4 Kalman 滤波实际使用流程4…...
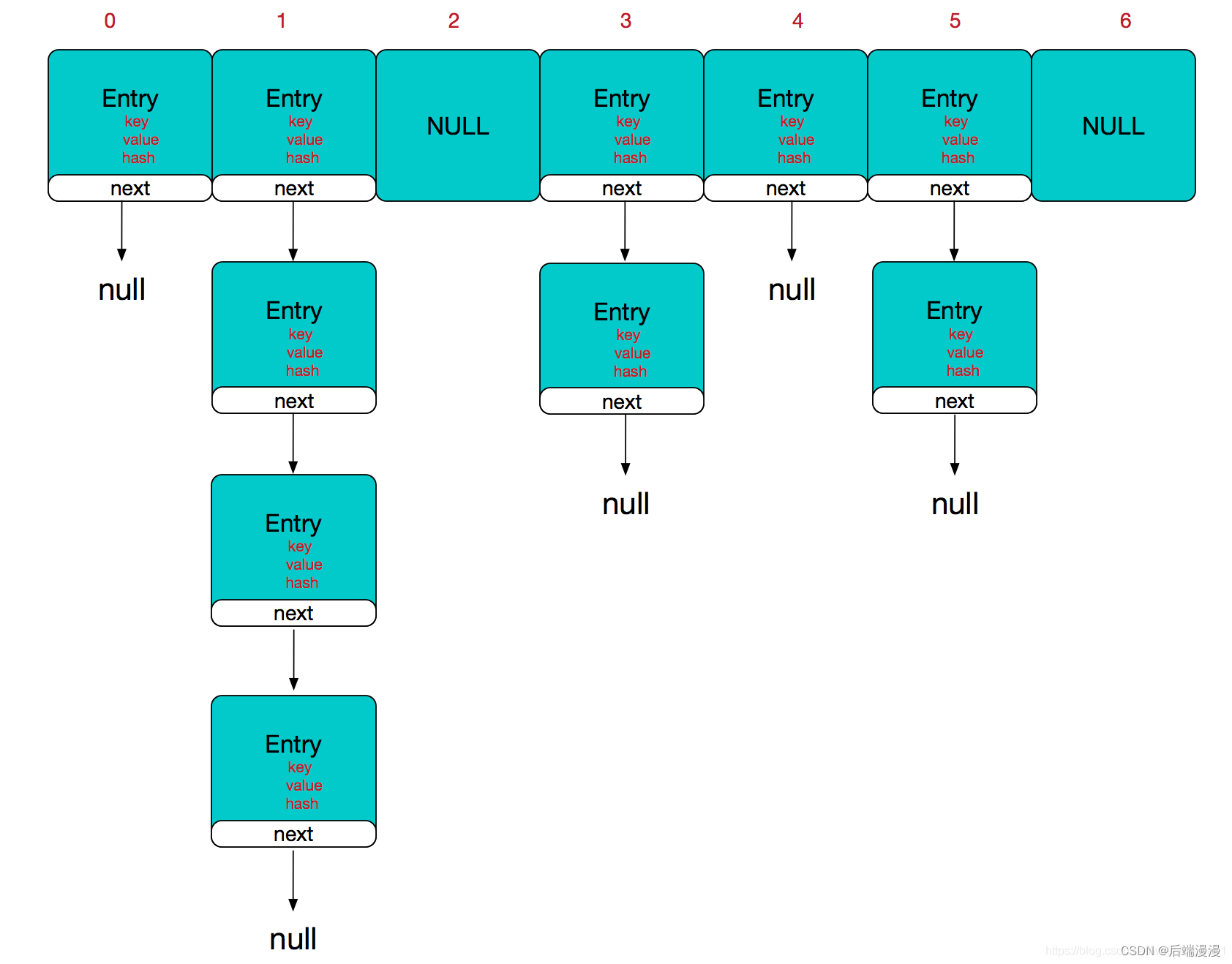
Java集合面试题：HashMap源码分析
文章目录一、HashMap源码二、HashMap数据结构模型图三、HashMap中如何确定元素位置四、关于equals与hashCode函数的重写五、阅读源码基本属性参考文章：史上最详细的 JDK 1.8 HashMap 源码解析参考文章：Hash详解参考文章：hashCode源码分析参考…...
华为OD机试 - 数组合并（Python）,真题含思路
数组合并 题目 现在有多组整数数组, 需要将他们合并成一个新的数组。 合并规则, 从每个数组里按顺序取出固定长度的内容合并到新的数组中, 取完的内容会删除掉, 如果该行不足固定长度或者已经为空, 则直接取出剩余部分的内容放到新的数组中, 继续下一行。 如样例 1, 获得长度…...
Vue2创建移动端项目
一、Vscode Vscode 下载安装以及常用的插件 1、Vscode 下载 下载地址：Vscode 中文语言插件 搜索 chinese 主题 Atom 主题 文件图标主题 搜索 icon 源代码管理插件GitLens 搜索 GitLens Live Server _本地服务器 搜索 Live Server Prettier - Code formatt…...
PorterDuffXfermode与圆角图片
版权声明 本文原创作者：谷哥的小弟作者博客地址：http://blog.csdn.net/lfdfhl 圆角图片 在项目开发中，我们常用到这样的功能：显示圆角图片。 这个是咋做的呢？我们来瞅瞅其中一种实现方式 /*** param bitmap 原图* p…...
如何准备大学生电子设计竞赛
大学生电子设计竞赛难度中上，一般有好几个类型题目可以选择，参赛者可以根据自己团队的能力、优势去选择合适自己的题目，灵活自主空间较大。参赛的同学们可以在暑假好好学习相关内容，把往年的题目拿来练练手。这个比赛含金量还是有…...
【Java容器（jdk17）】ArrayList深入源码，就是这么简单
ArrayList深入源码一、ArrayList源码解析1. MIXIN 的混入2. 属性说明3. 构造方法4. 其他方法（核心）iterator 和 listIterator 方法add方法remove 方法sort方法其他二、ArrayList 为什么是线程不安全的？体现哪些方面呢？三、ArrayLi…...
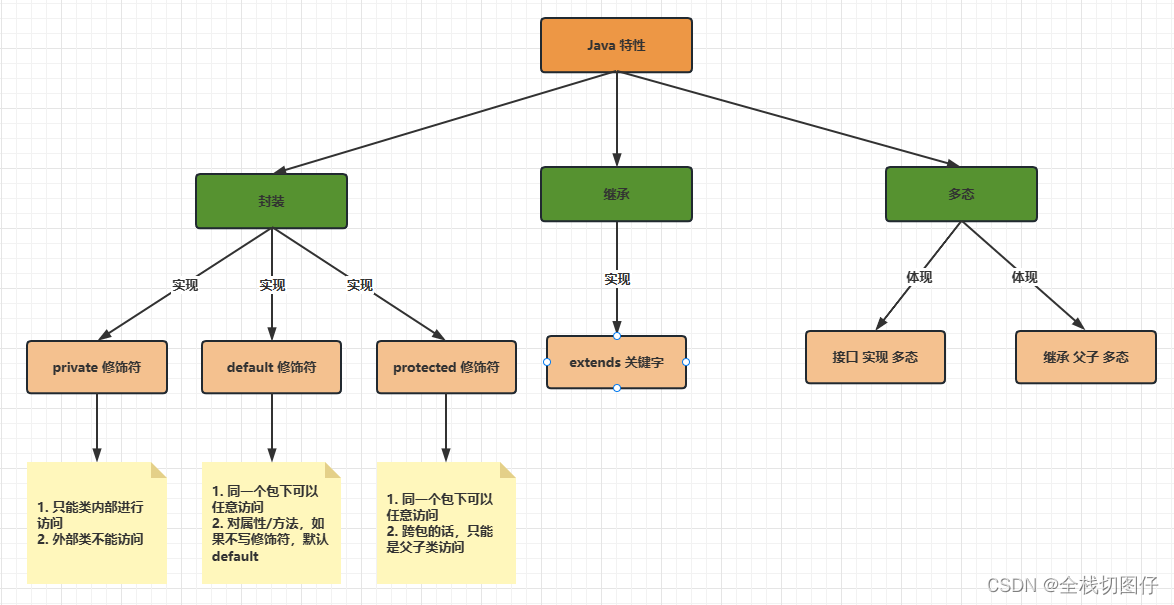
【Java 面试合集】简述下Java的三个特性 以及项目中的应用
简述下Java的特征 以及项目中的应用 1. 概述 上述截图中就是Java的三大特性，以及特性的实现方案。接下来就每个点展开来说说 2. 封装 满足：隐藏实现细节，公开使用方法 的都可以理解为是封装 而实现封装的有利手段就是权限修饰符了。可以根据…...
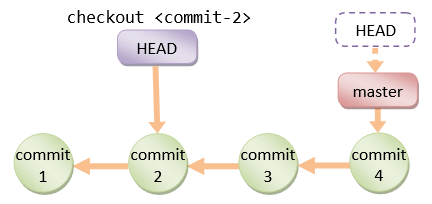
git基本概念图示【学习】
基本概念工作区（Working Directory）就是你在电脑里能看到的目录，比如名字为 gafish.github.com 的文件夹就是一个工作区本地版本库（Local Repository）工作区有一个隐藏目录 .git，这个不算工作区，…...
深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架，用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录，以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
Redis相关知识总结（缓存雪崩，缓存穿透，缓存击穿，Redis实现分布式锁，如何保持数据库和缓存一致）
文章目录 1.什么是Redis？2.为什么要使用redis作为mysql的缓存？3.什么是缓存雪崩、缓存穿透、缓存击穿？3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...
基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能，多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统，涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能，适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
高等数学（下）题型笔记（八）空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
Linux C语言网络编程详细入门教程：如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程：如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket（服务端和客户端都要）2. 绑定本地地址和端口&#x…...
数学建模-滑翔伞伞翼面积的设计，运动状态计算和优化 ！
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态，并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
基于单片机的宠物屋智能系统设计与实现（论文+源码）
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢，连接红外测温传感器，可实时精准捕捉宠物体温变化，以便及时发现健康异常；水位检测传感器时刻监测饮用水余量，防止宠物…...
ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物，因为每个访问一个线程局部变量的线程（通过其 get 或 set 方法）都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段，这些类希望将…...
VSCode 使用CMake 构建 Qt 5 窗口程序
首先，目录结构如下图： 运行效果： cmake -B build cmake --build build 运行： windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...