[递推与递归]数的计算
题目描述
给出正整数 n,要求按如下方式构造数列:
- 只有一个数字 n 的数列是一个合法的数列。
- 在一个合法的数列的末尾加入一个正整数,但是这个正整数不能超过该数列最后一项的一半,可以得到一个新的合法数列。
请你求出,一共有多少个合法的数列。两个合法数列 a,b不同当且仅当两数列长度不同或存在一个正整数 i≤∣a∣,使得 ai≠bi;
输入格式
输入只有一行一个整数,表示 n。
输出格式
输出一行一个整数,表示合法的数列个数。
输入输出样例
输入 #1
6
输出 #1
6
说明/提示
样例 1 解释
满足条件的数列为:
- 6
- 6,1
- 6,2
- 6,3
- 6,2,1
- 6,3,1
数据规模与约定
对于全部的测试点,保证 1≤n≤1000
解题分析
本题的递推其实并不困难,主要是关于递归函数的一个设计。我们假定f(n)表示对于给定的正整数n,它得到的序列个数。那么,我们可以将其与更小的数所形成的序列个数进行关联。例如说例子中的6, 它所形成的序列首先有它自己本身吧。然后,对于小于等于它的二分之一的数,都可以继续接在这个序列的后面。
所以,我们可以得到f(n)=f(1)+f(2)+....+f(m),其中m<=n/2,那么,本题就解决了。
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int dp[1005];
int f(int n){if(n==1){return 1;}if(dp[n]) return dp[n];int m=n/2;int res=1;for(int i=1;i<=m;i++){res+=f(i);}return dp[n]=res;
}int main(){int n; cin>>n;cout<<f(n)<<endl;return 0;
}相关文章:

[递推与递归]数的计算
题目描述 给出正整数 n,要求按如下方式构造数列: 只有一个数字 n 的数列是一个合法的数列。在一个合法的数列的末尾加入一个正整数,但是这个正整数不能超过该数列最后一项的一半,可以得到一个新的合法数列。 请你求出ÿ…...
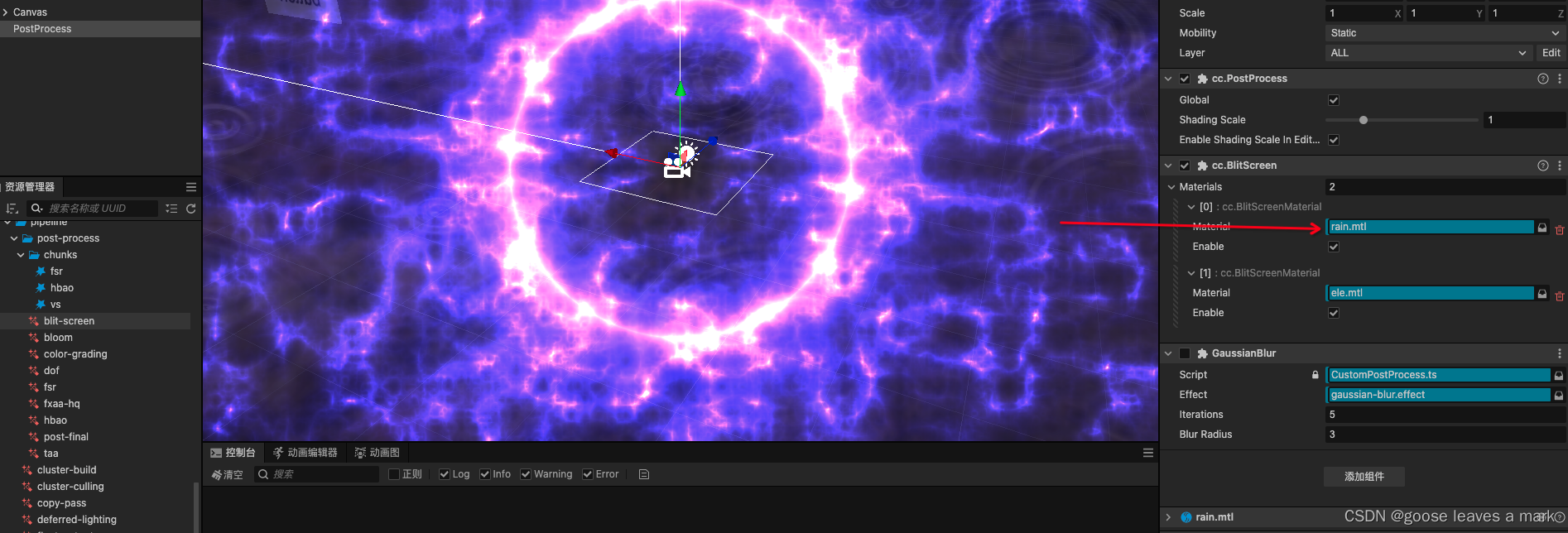
Cocos Creator 3.8.x 后效处理(前向渲染)
关于怎么开启后效效果我这里不再赘述,可以前往Cocos官方文档查看具体细节:后效处理官网 下面讲一下怎么自己定义一个后处理效果,想添加自己的后效处理的话只需要在postProcess节点下添加一个BlitScreen 组件即可,然后自己去添加自…...
【前端素材】推荐优质后台管理系统 Adminity平台模板(附源码)
一、需求分析 1、系统定义 后台管理系统是一种用于管理网站、应用程序或系统的管理界面,通常由管理员和工作人员使用。它提供了访问和控制网站或应用程序后台功能的工具和界面,使其能够管理用户、内容、数据和其他各种功能。 2、功能需求 后台管理系…...

身份证号与姓名实名认证接口-二要素实名认证-C++接口代码
翔云(https://www.netocr.com/idenNoOrd.html)身份证二要素实名认证接口在当今的数字化社会中扮演着至关重要的角色,它不仅守护着网络世界的秩序,也悄然影响着现实生活的点滴。看似普通的身份证号实名认证接口也在悄然守护着人们的…...
笑营宝高校选修课报名考勤系统源码开发方案
一、项目背景与目标 (一)项目背景 随着高等教育的普及和教学模式的不断创新,高校选修课程体系日趋复杂多变。学生对课程选择的自由度提高,使得传统的选课和考勤管理方式变得繁琐且效率低下。目前,许多高校仍然采用纸…...

类型字段定义影响WebApi传值及SqlSugar调用Select创建新对象
ASP.NET Core编写的WebApi,由于输入参数较多,专门定义了输入参数类并设置[FromBody]方式传值,但测试时始终无法通过postman将输入参数值传递给WebApi,condition对象的所有属性值一直都为空。同时在WebApi内部调用SqlSugar查询数据…...

golang 函数式编程库samber/mo使用: IO
golang 函数式编程库samber/mo使用: IO 如果您不了解samber/mo库, 请先阅读第一篇 Option 在函数式编程中,副作用和纯函数是最常见的概念。 IO用来封装IO这类副作用。 什么是副作用 副作用是在计算结果的过程中,改变了系统状态…...

在OceanBase使用中,如何优化因Join估算不准导致执行计划选错的问题
作者:胡呈清,爱可生公司旗下的DBA团队成员,擅长故障分析和性能优化。爱可生开源社区出品,原创内容未经授权不得随意使用,转载请联系小编并注明来源。本文约 1600 字,预计阅读需要 15 分钟。 数据库版本&…...
potplayer安装
官网 解压运行即可...

PostgreSQL 与MySQL 对比使用
一、前言 博主的系统既有 用到MySQL 也有用到PostgreSQL ,之所以用到这两种数据库,主要是现在都是国产替代,虽然说这两款数据库也不是国产的,但是相对开源,oracle是不让用了。所以现在使用比较多的就是这两个关系型数据…...

配置nginx代理访问openai接口
环境: 阿里云硅谷地区服务器,ubuntu22 操作步骤 1.安装nginx apt install nginx2.编辑文件/etc/nginx/sites-enabled/default,内容替换如下 server {listen 80;location / {proxy_pass https://api.openai.com;proxy_set_header Host api.…...
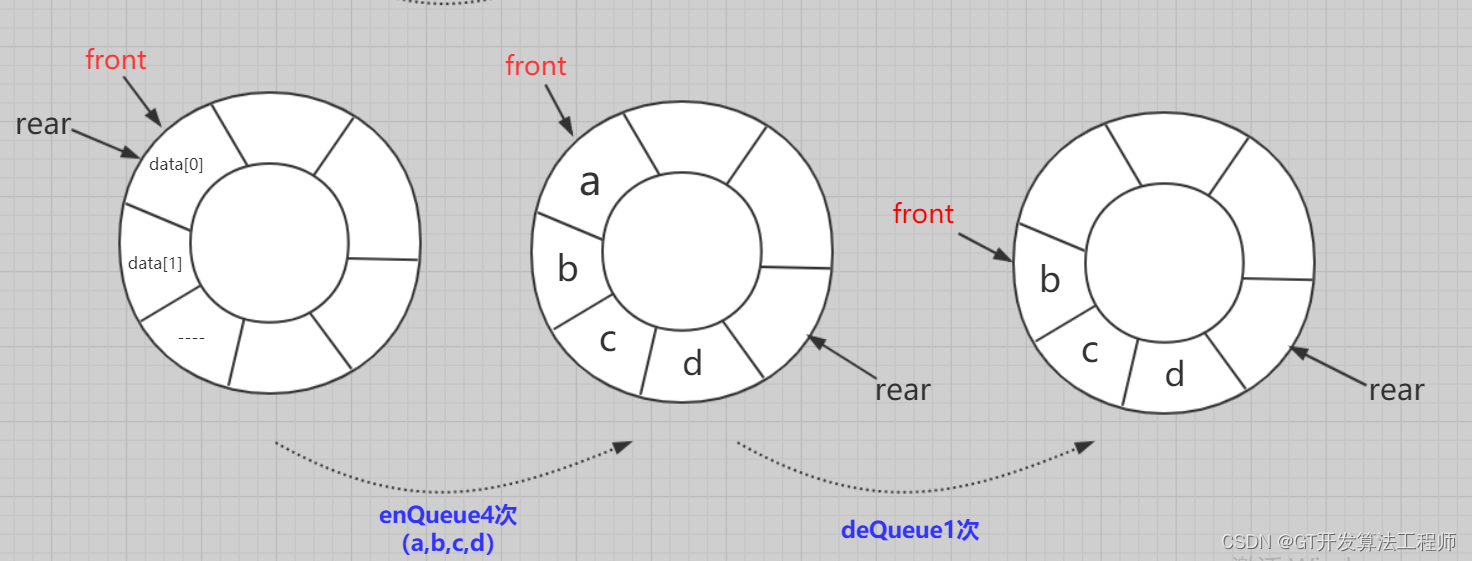
使用Python语言实现一个基于动态数组的序列队列
一、动态数组的实现 首先,我们需要创建一个DynamicArray类,该类将管理我们的动态数组。 动态数组能够动态地调整其大小,以容纳更多的元素。 目录 一、动态数组的实现 代码示例: 二、序列队列的实现 接下来,我…...
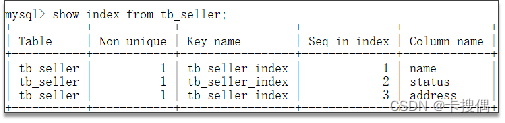
面试数据库篇(mysql)- 07索引创建原则与失效及优化
索引创建原则 1). 针对于数据量较大,且查询比较频繁的表建立索引。 2). 针对于常作为查询条件(where)、排序(order by)、分组(group by)操作的字段建立索引。 3). 尽量选择区分度高的列作为索引,尽量建立唯一索引,区分度越高,使用索引的效率越高。 4). 如果是字符…...

《互联网的世界》第三讲-tcp
dns 找到了地址,spf 确定了路径,如何运输数据呢?今天讲 tcp。 计算机网络领域的特定技术是最后当你干这个事时才要用的,我对孩子们这样说,实际上你可以随便看一个快递单子来理解端到端传输协议。 源地址,…...

JOSEF约瑟 JZS-7G-42 AC220V静态可调延时中间继电器 端子式导轨安装15ms-10s
系列型号:JZS-7G-57端子排延时中间继电器;JZS-7G-42X端子排延时中间继电器;JZS-7G-22X端子排延时中间继电器;JZS-7G-21端子排延时中间继电器;JZS-7G-41端子排延时中间继电器;JZS-7G-51端子排延时中间继电器…...

Hudi配置参数优化
1)Commits:表示一批记录原子性的写入到一张表中。 2)Cleans:清除表中不再需要的旧版本文件。 3)Delta_commit:增量提交指的是将一批记录原子地写入MergeOnRead类型表,其中一些/所有数据都可以写入增量日志。 4&…...

适用Java SpringBoot项目的分布式锁
在分布式系统中,常用到分布式锁,它有多中实现方式,如:基于redis,database,zookeeper等。Spring integration组件有这三种服务的分布式锁实现,今天来看看用的比较多的redis和database实现方式。 …...
面试笔记系列二之java基础+集合知识点整理及常见面试题
目录 Java面向对象有哪些特征,如何应用 Java基本数据类型及所占字节 Java中重写和重载有哪些区别 jdk1.8的新特性有哪些 内部类 1. 成员内部类(Member Inner Class): 2. 静态内部类(Static Nested Class&#…...
搭建LNMP环境并搭建论坛和博客
目录 一、LNMP架构原理 二、编译安装Nginx 三、编译安装MySQL 四、编译安装PHP 五、配置Nginx支持PHP解析 六、安装论坛 七、安装博客 一、LNMP架构原理 LNMP架构,是指在Linux平台下,由运行Nginx的web服务器,运行PHP的动态页面解析程序…...

蓝桥杯刷题2
1. 修建灌木 import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scan new Scanner(System.in);int n scan.nextInt();for (int i 1;i < n1;i){int distance Math.max(i-1,n-i);System.out.println(distance*2);}scan.close…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 )
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
