AcWing1049.大盗阿福题解
前言
如果想看状态机的详解,点机这里:dp模型——状态机模型C++详解
1049. 大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T,表示一共有 T组数据。
接下来的每组数据,第一行是一个整数 N,表示一共有 N家店铺。
第二行是 N个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
1≤T≤50,
1≤N≤1e5
输入样例:
2
3
1 8 2
4
10 7 6 14输出样例:
8
24样例解释
对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。
对于第二组样例,阿福选择第1和4家店铺行窃,获得的现金数量为10+14=24。
这道题的大意就是,有t组数据,每个有n个超市,告诉你每一家的价钱,不能盗窃相邻的超市。
计算大盗能获得的最大利益。
解题思路
这道题有两种解法,第一种是普通的线性dp,第二种是状态机dp。
第一种
用f[i]表示前i家商店阿福可以获得的最大价值。
对于第i次选择,只能选偷或者不偷,偷就是f[i - 2] + w[i], 不偷就是f[i - 1]。
状态转移方程就是:
f[i] = max(f[i - 2] + w[i], f[i - 1]);完整ac代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, INF = 1e9;
int t, n;
int w[N], f[N];
int main() {scanf("%d", &t);while(t--) {scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%d", &w[i]);memset(f, -INF, sizeof f);f[0] = 0;for(int i = 1; i <= n; i++) f[i] = max(f[i - 2] + w[i], f[i - 1]);printf("%d\n", f[n]);}return 0;
}第二种就是今天讲到的状态机了,对于第i个超市,可以选择偷或者不偷,我们用1表示偷,0表示不偷(都是当前的超市)。

状态转移方程就是:
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + w[i];ac代码如下:
#include <bits/stdc++.h>
using namespace std;
#define read(a) scanf("%d", &a);
const int N = 1e5 + 10, INF = 1e9;
int t, n;
int w[N], f[N][2];
int main() {read(t);while(t--) {read(n);for(int i = 1; i <= n; i++) read(w[i]);f[0][0] = 0, f[0][1] = -INF;for(int i = 1; i <= n; i++) {f[i][0] = max(f[i - 1][0], f[i - 1][1]);f[i][1] = f[i - 1][0] + w[i];}printf("%d\n", max(f[n][1], f[n][0]));}return 0;
}相关文章:

AcWing1049.大盗阿福题解
前言如果想看状态机的详解,点机这里:dp模型——状态机模型C详解1049. 大盗阿福阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有 N家店铺,每家店中都有一些现金。阿福事先调查得知,只有当…...

python日志模块,loggin模块
python日志模块,loggin模块loggin模块日志的格式处理器种类日志格式的参数使用loggin模块 logging库采用模块化方法,并提供了几类组件:记录器,处理程序,过滤器和格式化程序。 记录器(Logger)&a…...
接口自动化入门-TestNg
目录1.TestNg介绍2、TestNG安装3、TestNG使用3.1 编写测试用例脚本3.2 创建TestNG.xml文件(1)创建testng.xml文件(2)修改testng.xml4、测试报告生成1.TestNg介绍 TestNg是Java中开源的自动化测试框架,灵感来源于Junit…...

Spring AOP —— 详解、实现原理、简单demo
目录 一、Spring AOP 是什么? 二、学习AOP 有什么作用? 三、AOP 的组成 3.1、切面(Aspect) 3.2、切点(Pointcut) 3.3、通知(Advice) 3.4、连接点 四、实现 Spring AOP 一个简…...

(蓝桥真题)异或数列(博弈)
题目链接:P8743 [蓝桥杯 2021 省 A] 异或数列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 4 1 1 1 0 2 2 1 7 992438 1006399 781139 985280 4729 872779 563580 样例输出: 1 0 1 1 分析:容易想到对于异或最大值…...

4万字数字政府建设总体规划方案WORD
本资料来源公开网络,仅供个人学习,请勿商用。部分资料内容: 我省“数字政府”架构 (一) 总体架构。 “数字政府”总体架构包括管理架构、业务架构、技术架构。其中,管理架构体现“管运分离”的建设运营模式…...

CCF/CSP 201709-2公共钥匙盒100分
试题编号:201709-2试题名称:公共钥匙盒时间限制:1.0s内存限制:256.0MB问题描述:问题描述 有一个学校的老师共用N个教室,按照规定,所有的钥匙都必须放在公共钥匙盒里,老师不能带钥…...

【OC】Blocks模式
1. Block语法 Block语法完整形式如下: ^void (int event) {printf("buttonId:%d event%d\n", i, event); }完整形式的Block语法与一般的C语言函数定义相比,仅有两点不同。 没有函数名。带有“^”(插入记号)。 因为O…...
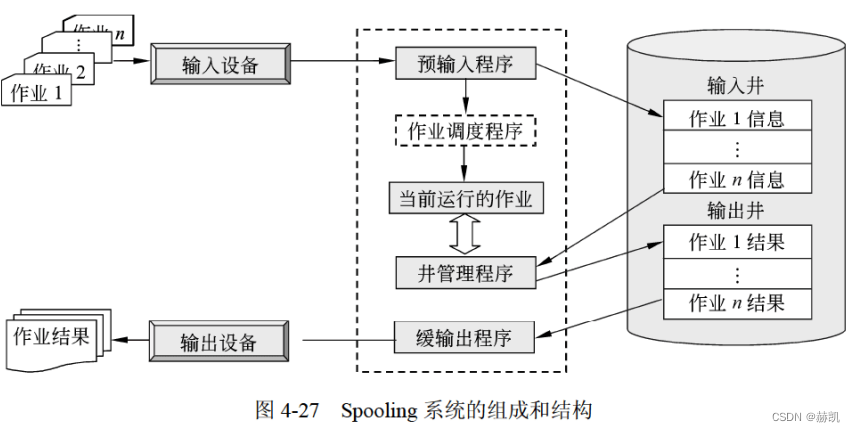
软件设计师教程(七)计算机系统知识-操作系统知识
软件设计师教程 软件设计师教程(一)计算机系统知识-计算机系统基础知识 软件设计师教程(二)计算机系统知识-计算机体系结构 软件设计师教程(三)计算机系统知识-计算机体系结构 软件设计师教程(…...

蓝桥杯2023/3/2
1. 小蓝正在学习一门神奇的语言,这门语言中的单词都是由小写英文字母组 成,有些单词很长,远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词,他准备不再完全记忆这些单词,而是根据单词中哪个字母出现得最…...

【IoT】创业成功不可或缺的两个因素:能力和趋势
今天就来谈谈能力和趋势究竟哪个更重要的问题。 在谈成功的十大要素时,我曾经讲到: 一命、二运、三风水,这三个要素几乎不涉及任何个人的努力。 而趋势跟这三个要素又是息息相关的,这也类似雷军所说的飞猪理论。 只要风足够大&…...

2020蓝桥杯真题日期格式 C语言/C++
问题描述 小蓝要处理非常多的数据, 其中有一些数据是日期。 在小蓝处理的日期中有两种常用的形式: 英文形式和数字形式。 英文形式采用每个月的英文的前三个宁母作为月份标识, 后面跟两位数字 表示日期, 月份标识第一个字母大写, 后两个字母小写, 日期小于 10 时要补 前导 0s…...
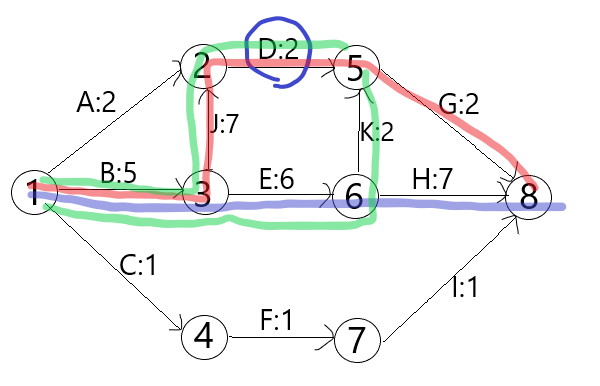
总时差与自由时差
定义总时差(总浮动时间)(TF,Total Free Time,不耽误项目总进度)LS(Latest Start)-ES(Earliest Start)LF(Latest Finish)-EF࿰…...

LeetCode两个数组的交集-跳跃游戏- 最长有效括号
两个数组的交集 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 示例 1: 输入:nums1 [1,2,2,1], nums2 [2,2] 输出:[2] 示例 2: 输入&…...

mysql普通索引与唯一索引怎么选择
学习mysql普通索引与唯一索引选择记录总结,学习链接:http://gk.link/a/11YG8从mysql查询操作分析:普通索引:查到满足条件的第一条记录后,还会继续查找下一条记录,直到出现满足条件的记录出现后停止检索唯一…...
JavaWeb开发(三)3.5——Java的反射机制
一、反射机制的概念 指在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法,对于任意一个对象,都能调用它的任意一个方法。这种动态获取信息,及动态调用对象方法的功能叫java语言的反射机制。 Java反射机制的核心是在程序运行时动…...

Python每日一练(20230305)
目录 1. 正则表达式匹配 ★★★ 2. 寻找旋转排序数组中的最小值 II ★★★ 3. 删除排序链表中的重复元素 II ★★ 1. 正则表达式匹配 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 . 和 * 的正则表达式匹配。 . 匹配任意单个字符* 匹配零个或多个…...

SpringBoot三种方法实现定时发送邮件的案例
前言 小编我将用CSDN记录软件开发之路上所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习,让我们共…...
opengl、opengl es、webgl介绍与opengl开发入门
1、OpenGL OpenGL(英语:Open Graphics Library,译名:开放图形库或者“开放式图形库”)常用于CAD、虚拟现实、科学可视化程序和电子游戏开发。OpenGL的高效实现(利用了图形加速硬件)存在于Windo…...
Vue3之组件间传值
何为组件间传值 在Vue3之组件文章中,我们学会了定义使用组件,但是我们似乎还缺少什么将组件之间联系起来,说到组件之间的联系就不得不提组件间的传值,而组件间的传值其实也不难理解,就是如何在子组件中接收到父组件传…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
