Python线性代数傅里叶分析和动态系统模拟分析之一
要点
- Python向量数值计算、可视化,线性独立性和子空间。
- 了解欧几里德距离、余弦相似度和皮尔逊相关性应用案例:Python数值计算文档相似度
- 时间序列和特征检测示例:Python信号处理边缘检测器, K均值示例:随机簇质心分布
- Python傅里叶分析应用示例:心电图频谱,消除音频噪音
- Python数值计算和可视化矩阵,几何变换及示例:图像特征检测
- Python计算矩阵逆计算,正交矩阵和 QR 分解,行缩减,LU 分解和最小二乘法,示例:QR与格拉姆-施密特过程和主成分分析,多变量分析和协同过滤领域最小二乘法,根据天气预测自行车租赁最小二乘法,多项式回归最小二乘法 ,网格搜索查找模型参数最小二乘法
线性代数
以下是线性代数 4 个核心概念的细分、它们的重要性、上下文解释和 Python 代码片段:
向量和矩阵运算
向量和矩阵是处理数据和参数的基础。运算(加法、乘法、转置)使算法计算能够以矢量化(高效)的方式进行。
- 向量:可以存储数据或参数的一维数组。
- 矩阵:用于存储数据集或转换数据的二维数组。
import numpy as npvector = np.array([2, 3])
matrix = np.array([[1, 2], [3, 4]])sum_vector_matrix = vector + matrix[0] # Addition
print(sum_vector_matrix)
product = np.dot(matrix, vector) # Multiplication
print("product: ",product)transpose = matrix.T # Transpose
print(transpose)
输出:
[3 5]
product: [ 8 18]
[[1 3][2 4]]
特征值和特征向量
特征值和特征向量有助于深度学习模型中的降维、主成分分析和系统稳定性分析。
- 特征向量是非零向量,在应用线性变换时仅按标量因子变化。标量是特征值。
import numpy as np
import matplotlib.pyplot as pltA = np.array([[4, 2], [1, 3]])eigenvalues, eigenvectors = np.linalg.eig(A)print(f'Eigenvalues: {eigenvalues}')
print(f'Eigenvectors: {eigenvectors}')origin = [0], [0]plt.quiver(*origin, eigenvectors[0,0], eigenvectors[1,0], color=['r'], scale=3, scale_units='xy', angles='xy')
plt.quiver(*origin, eigenvectors[0,1], eigenvectors[1,1], color=['b'], scale=3, scale_units='xy', angles='xy')plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.title('Eigenvectors of A')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid()
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.show()
输出:[^f1]
Eigenvalues: [5. 2.]
Eigenvectors: [[ 0.89442719 -0.70710678][ 0.4472136 0.70710678]]
线性变换
线性变换(缩放、旋转)对于机器学习中的数据增强、标准化和数据转换至关重要。
- 线性变换改变数据的空间和形状,同时保留网格线的直线度和平行度。
import numpy as np
import matplotlib.pyplot as pltmatrix = np.array([[2, 3], [3, 4]])scaling_matrix = np.array([[2, 0], [0, 2]])transformed_matrix = np.dot(matrix, scaling_matrix)plt.scatter(matrix[:,0], matrix[:,1], color="blue", label="Original")
plt.scatter(transformed_matrix[:,0], transformed_matrix[:,1], color="red", label="Transformed")plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title('Linear Transformation: Scaling')
plt.grid(True)
plt.legend()
plt.axis('equal')
plt.show()
输出:
求解线性系统
求解线性系统有助于找到权重、优化算法以及在机器学习模型中进行预测。
- 给定 A x = B Ax = B Ax=B,其中 A A A 是矩阵, B B B 是向量,找到满足方程的向量 x x x。
例如:
2 x + 3 y = 1 4 x − 5 y = 2 \begin{aligned} & 2 x+3 y=1 \\ & 4 x-5 y=2 \end{aligned} 2x+3y=14x−5y=2
import numpy as npA = np.array([[2, 3], [4, -5]])
B = np.array([1, 2])x = np.linalg.solve(A, B)print(f'Solution: x = {x[0]:.2f}, y = {x[1]:.2f}')
输出:
Solution: x = 0.50, y = 0.00
傅里叶分析
傅里叶分析是研究如何将一般函数分解为具有确定频率的三角函数或指数函数。 傅里叶展开有两种类型:
- 傅立叶级数:如果一个(表现相当良好的)函数是周期性的,那么它可以写成具有特定频率的三角函数或指数函数的离散和。
- 傅里叶变换:不一定是周期性的(但仍然表现得相当良好)的一般函数可以写成三角函数或指数函数的连续积分,具有可能频率的连续体
傅立叶分析在物理学中如此重要的原因是,控制物理系统的许多(尽管肯定不是全部)微分方程都是线性的,这意味着两个解的和又是一个解。 因此,由于傅立叶分析告诉我们任何函数都可以写成正弦函数,因此我们在求解微分方程时,可以将注意力限制在这些函数上。 然后我们可以从这些特殊的函数中构建任何其他函数。 这是一个非常有用的策略,因为处理正弦函数总是比处理一般函数更容易。
Python傅里叶变换示例
[^f2]傅立叶变换 (FT) 将信号的时域与其频域相关联,其中频域包含有关构成信号的正弦曲线(幅度、频率、相位)的信息。 由于FT是连续变换,离散傅立叶变换(DFT)成为数字世界中适用的变换,它将离散格式的信号信息保存为一组样本,其中采样定理是离散化的严格规则, 信号。 具有 N 个样本的信号 (xn) 的 DFT 由以下等式给出:
X k = ∑ n = 0 N − 1 x n ⋅ e − i 2 π k n / N = ∑ n = 0 N − 1 x n ⋅ [ cos ( 2 π k n / N ) − i sin ( 2 π k n / N ) ] X_k=\sum_{n=0}^{N-1} x_n \cdot \mathrm{e}^{-\mathrm{i} 2 \pi k n / \mathrm{N}}=\sum_{n=0}^{N-1} x_n \cdot[\cos (2 \pi k n / N)-i \sin (2 \pi k n / N)] Xk=n=0∑N−1xn⋅e−i2πkn/N=n=0∑N−1xn⋅[cos(2πkn/N)−isin(2πkn/N)]
其中:
- N \mathrm{N} N : 样本数量
- n \mathrm{n} n : 当前样本
- k \mathrm{k} k : 当前频率 k ∈ [ 0 , N − 1 ] \mathrm{k} \in[0, \mathrm{~ N}-1] k∈[0, N−1]
- x n x_n xn:样本 n \mathrm{n} n 处的正弦值
- X k X_k Xk:包含幅度和相位信息的 DFT
DFT ( X k X_k Xk) 的输出是一个复数数组,其中包含频率分量的信息。 使用数学方程对信号应用 DFT 直接需要大量的计算复杂性。 幸运的是,快速傅立叶变换 (FFT) 的开发可以提供更快的 DFT 实现。 FFT 利用了 DFT 输出的对称性。
我们将开始简单地了解本文中使用的每种方法的输入和输出。 首先,我们将导入所需的包。 Numpy 用于处理矩阵和计算。 我们从 scipy.fft 模块(fft、rfft、fftfreq、rfftfreq)导入有助于我们进行傅立叶分析相关计算的方法。 最后,Plotly 和 matplotlib 用于可视化。
import numpy as np
from scipy.fft import fft, rfft
from scipy.fft import fftfreq, rfftfreq
import plotly.graph_objs as go
from plotly.subplots import make_subplots
import matplotlib.pyplot as plt
%matplotlib inline
我们需要信号来尝试我们的代码。 正弦曲线很棒并且适合我们的示例。 在接下来的代码中,我们使用名为 Signal 的类生成正弦信号,您可以按照此要点找到该类,以便随时使用。 我们将使用前一类生成的信号,包含三个正弦曲线 (1, 10, 20) Hz,幅度分别为 (3, 1, 0.5)。 采样率为 200,信号持续时间为 2 秒。
# Generate the three signals using Signal class and its method sine()
signal_1hz = Signal(amplitude=3, frequency=1, sampling_rate=200, duration=2)
sine_1hz = signal_1hz.sine()
signal_20hz = Signal(amplitude=1, frequency=20, sampling_rate=200, duration=2)
sine_20hz = signal_20hz.sine()
signal_10hz = Signal(amplitude=0.5, frequency=10, sampling_rate=200, duration=2)
sine_10hz = signal_10hz.sine()# Sum the three signals to output the signal we want to analyze
signal = sine_1hz + sine_20hz + sine_10hz# Plot the signal
plt.plot(signal_1hz.time_axis, signal, 'b')
plt.xlabel('Time [sec]')
plt.ylabel('Amplitude')
plt.title('Sum of three signals')
plt.show()
可以使用 scipy 包中的 (fft) 计算该信号的傅立叶变换,如下所示
# Apply the FFT on the signal
fourier = fft(signal)# Plot the result (the spectrum |Xk|)
plt.plot(np.abs(fourier))
plt.show()
现在我们已经了解了傅立叶分析中使用的每种方法的输入和输出,让我们开始编写最终代码。 我们将建立一个类(Fourier),让我们对傅里叶变换的使用更加方便、更好用。
现实应用:心电图频谱、消除音频噪音
动态系统模拟分析
参阅一:计算思维
参阅二:亚图跨际
相关文章:

Python线性代数傅里叶分析和动态系统模拟分析之一
要点 Python向量数值计算、可视化,线性独立性和子空间。了解欧几里德距离、余弦相似度和皮尔逊相关性应用案例:Python数值计算文档相似度时间序列和特征检测示例:Python信号处理边缘检测器, K均值示例:随机簇质心分布Python傅里叶…...
)
mysql插入GEOMETRY相关字段类型(point,linestring等)
一、问题 向mysql中插入point,linestring等相关空间坐标字段,出现报错: 1416 - Cannot get geometry object from data you send to the GEOMETRY field要插入的数据:...

vue3学习 【5】watch的使用
什么是watch 当我们需要根据一个数据的变化来进行一些操作的时候我们需要使用侦听器,它能够在响应式数据发生变化的时候触发提供的回调函数 基础侦听 watch 可以侦听不同的数据源。例如: ref计算属性响应式对象getter函数多个数据源组层的数据 cons…...
PyTorch深度学习快速入门
PyTorch深度学习快速入门 1.PyTorch环境配置及安装2.python编辑器的选择、安装、配置(pycharm、JupyTer安装)3.为什么torch.cuda.is_available()返回false4.python学习中两大法宝函数(也可用在pytorch)5.pycharm和jupyter…...
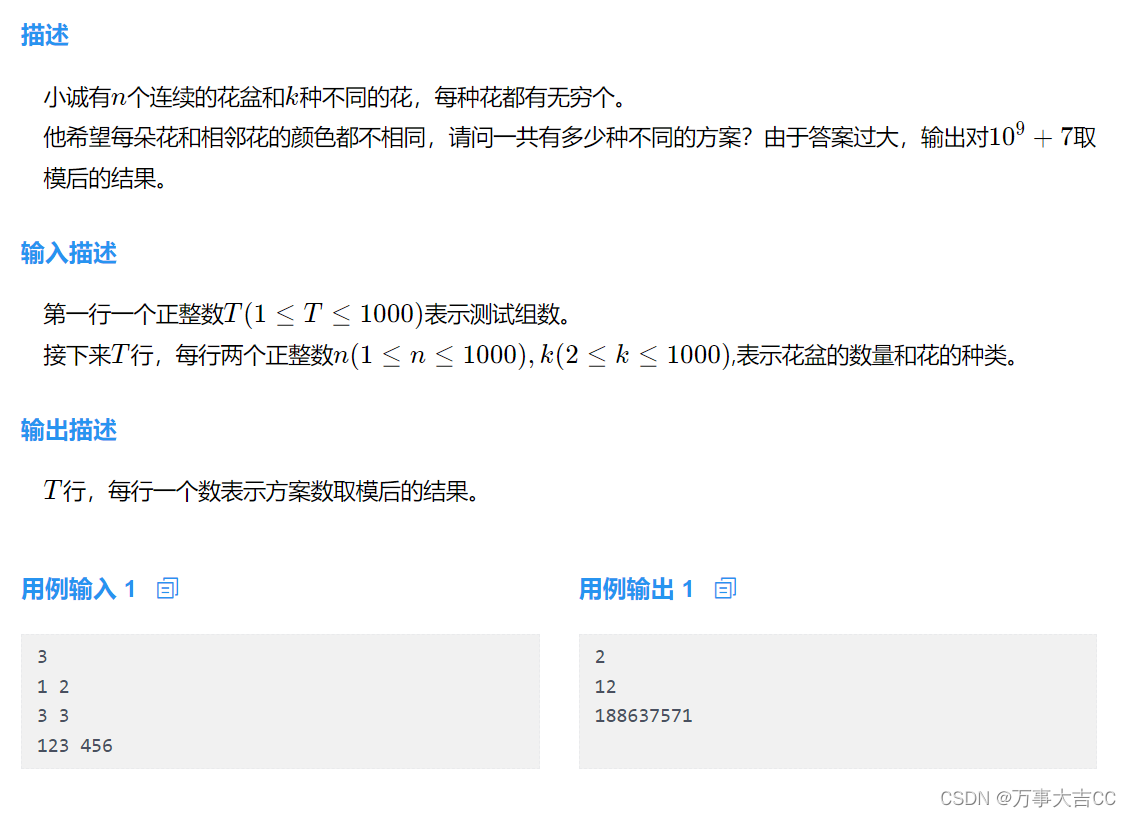
种花
分情况: 第一盆k种选择,之后全部k-1种选择 每次相乘结果对1e97取模 #include <iostream> #include <vector> #include <algorithm> using namespace std; #define endl \n const int N 1e9 7;int main() {ios::sync_with_stdio(f…...
)
Android Shadow插件化框架分析与集成(二)
本文索引 前言插件打包后如何交给宿主使用?宿主加载插件代码分析全局初始化操作加载插件activity测试过程中遇到的问题报错 1 :报错2:报错3 :二次开发支持多插件、多进程功能mPpsController 的构造方式mPluginLoader的构造方式多插件如何改造前言...

Go 与 Rust:导航编程语言景观
在当今构建软件时,开发者在编程语言上有着丰富的选择。两种脱颖而出的语言是 Go 和 Rust - 都很强大但却截然不同。本文将从各种因素比较这两种语言,以帮助您确定哪种更适合您的需求。 我们将权衡它们在并发、安全性、速度、互操作性等方面的方法。我们将…...

包管理工具之npm也慌了?
起因 因为npm的种种问题,我很早就换成了pnpm和yarn(但是其实npm也在使用),已经很久没有关注npm的功能更新了。最近无意间进入Node18版本的安装目录,发现其除了常规的node,npm等默认安装了一个新的包corepack,这个就是今天我要分享的东西了。 注: 我因为18版本的node上…...
mobile app 安全扫描工具MobSF了解下
可以干啥: static 静态分析 dynamic 动态分析 可以用来渗透了 如何docker安装 docker image 下载地址https://hub.docker.com/r/opensecurity/mobile-security-framework-mobsf/ setup 两行即可 1 docker pull opensecurity/mobile-security-framework-mobsf…...

Gophish+EwoMail 自建钓鱼服务器
GophishEwoMail 自建钓鱼服务器 文章目录 GophishEwoMail 自建钓鱼服务器1.前提准备2.搭建EwoMail邮件服务器1)Centos7 防火墙操作2)设置主机名3)host配置4)安装EwoMail5)获取DKIM6)端口服务介绍7ÿ…...

Dockerfile(5) - CMD 指令详解
CMD 指定容器默认执行的命令 # exec 形式,推荐 CMD ["executable","param1","param2"] CMD ["可执行命令", "参数1", "参数2"...]# 作为ENTRYPOINT的默认参数 CMD ["param1","param…...
使用 Gradle 版本目录进行依赖管理 - Android
/ 前言 / 在软件开发中,依赖管理是一个至关重要的方面。合理的依赖版本控制有助于确保项目的稳定性、安全性和可维护性。 Gradle版本目录(Version Catalogs)是 Gradle 构建工具的一个强大功能,它为项目提供了一种集中管理依赖…...
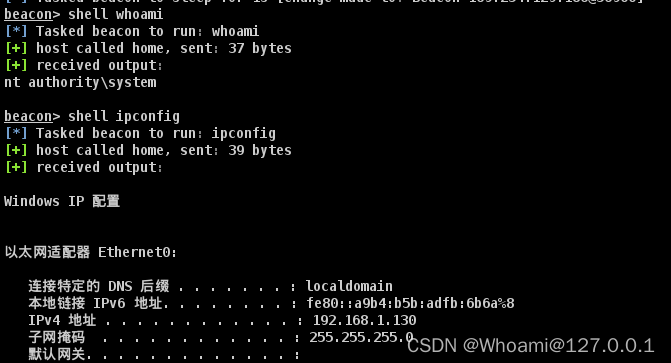
CS_上线三层跨网段机器(完整过程还原)
以前讲过用cs_smb_beacon上线不出网机器,但是真实的网络拓扑肯定不止这么一层的网络! 所以我就来搭建一个复杂一点的网络环境!! 当然了,这三台电脑之间都是不同的网段,(但是同属于一个域环境&a…...

crpto 的AES算法解密为空
1. 需求 对用户密码加密存入数据库,修改密码时取出密码在前端解密(保证密码前后端传输过程中为密文)。 文档地址:CryptoJS - CryptoJS (gitbook.io) 2. 原代码 2.1 加密 var userpass "123456"; var aseKey &quo…...

13.网络游戏逆向分析与漏洞攻防-网络通信数据包分析工具-如果没有工具就创造工具
内容参考于: 易道云信息技术研究院VIP课 上一个内容 :12.游戏网络通信存在的问题 现在把游戏网络的架构看了一个小小的大概,可以用它的接口发数据接收数据了,如果真正想用它这一套东西,真正核心不在于它的接口而在于…...
配置artifactory的反向代理和域名访问
一、概述 在许多情况下,组织会通过反向代理来提供对 Artifactory 的访问。在某些情况下,例如使用 Artifactory 作为 Docker 注册表,这种设置甚至是强制性的。为了简化反向代理的配置,Artifactory 提供了生成反向代理的功能&#x…...

python爬虫之协程知识点记录
一、协程 概念 协程 又称微线程(纤程),是一种用户态的轻量级线程 子程序 在所有的语言中都是层级调用的,比如A中调用B,B在执行过程中调用C,C执行完返回,B执行完返回,最后是A执行完毕。这是通过栈实现的&a…...
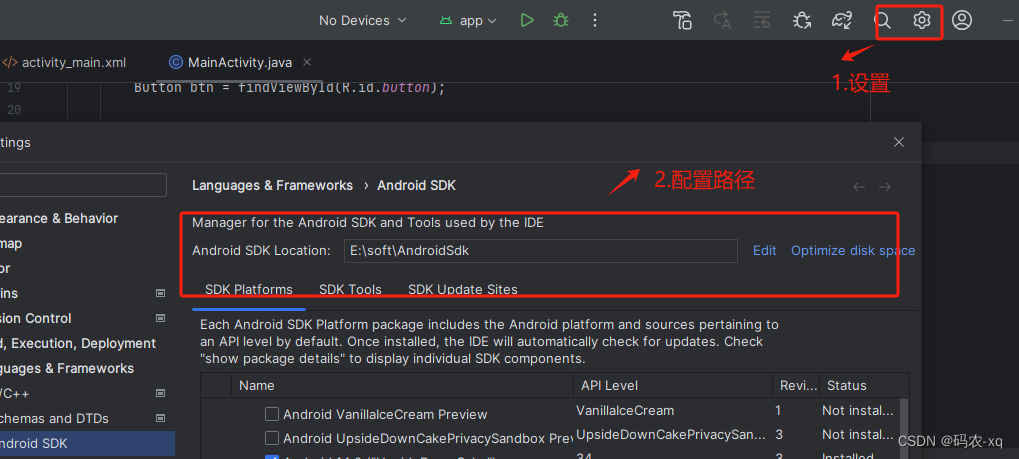
安卓开发1- android stdio环境搭建
安卓开发1-android stdio环境搭建 Jdk环境搭建 1. 准备Jdk,这边已经准备好了jdk1.8.0,该文件直接使用即可 2. 系统变量添加 %JAVA_HOME%\bin JAVA_HOME 3. 系统变量,Path路径添加 4. 添加完成后,输入命令javac / java -version,验证环…...

qt QRadioButton 及QButtonGroup 使用
QRadioButton 放在组合框QGroupBox中,再点击时,即使有多个QRadioButton按钮,同时选中的也就只有一个。 如下图所示, 对于多个QRadioButton,每个按钮都写一个槽函数是不太明智的选择,需要将QRadioButton放在…...
)
【LeetCode-178】最长重复子串(动归)
目录 LeetCode718.最长重复子串 题目描述 解法1:动态规划 代码实现 题目链接 题目描述 给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。 示例: 输入: A: [1,2,3,2,1] B: [3,2,1,4,7] 输出&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
