【LeetCode-178】最长重复子串(动归)
目录
LeetCode718.最长重复子串
题目描述
解法1:动态规划
代码实现
题目链接
题目描述
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
-
A: [1,2,3,2,1]
-
B: [3,2,1,4,7]
-
输出:3
-
解释:长度最长的公共子数组是 [3, 2, 1] 。
提示:
-
1 <= len(A), len(B) <= 1000
-
0 <= A[i], B[i] < 100
解法1:动态规划
本题其实是动规解决的经典题目,我们只要想到 用二维数组可以记录两个字符串的所有比较情况,这样就比较好推 递推公式了。 分析如下:
-
确定dp数组(dp table)以及下标的含义
dp[i]:以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dpi。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
此时细心的同学应该发现,那dp[0]是什么含义呢?总不能是以下标-1为结尾的A数组吧。其实dp[i]的定义也就决定着,我们在遍历dp[i]的时候i 和 j都要从1开始。那有同学问了,我就定义dp[i]为 以下标i为结尾的A,和以下标j 为结尾的B,最长重复子数组长度。不行么?
行倒是行! 但实现起来就麻烦一点,需要单独处理初始化部分,在本题解下面的拓展内容里,我给出了 第二种 dp数组的定义方式所对应的代码和讲解,大家比较一下就了解了。
-
确定递推公式
根据dpi的定义,dpi的状态只能由dpi - 1推导出来。即当A[i - 1] 和B[j - 1]相等的时候,dpi = dp[i - 1] + 1;根据递推公式可以看出,遍历i 和 j 要从1开始!
-
dp数组如何初始化
根据dpi的定义,dp[i] 和dp[0]其实都是没有意义的!但dp[i]和dp[0]要初始值,因为 为了方便递归公式dp[i] = dp[i - 1] + 1;
所以dp[i] 和dp[0]初始化为0。
举个例子A[0]如果和B[0]相同的话,dp[1] = dp[0] + 1,只有dp[0]初始为0,正好符合递推公式逐步累加起来。
-
确定遍历顺序
外层for循环遍历A,内层for循环遍历B。
代码实现
class Solution {public int findLength(int[] nums1, int[] nums2) {int len1 = nums1.length;int len2 = nums2.length;int max = 0;int[][] dp = new int[len1][len2];
for (int i = 0; i < len1; i++) {if (nums1[i] == nums2[0]) dp[i][0] = 1;max = Math.max(max, dp[i][0]);}for (int i = 0; i < len2; i++) {if (nums2[i] == nums1[0]) dp[0][i] = 1;max = Math.max(max, dp[0][i]);}
for (int i = 1; i < len1; i++) {for (int j = 1; j < len2; j++) {if (nums1[i] == nums2[j]) {dp[i][j] = dp[i-1][j-1] + 1;max = Math.max(max, dp[i][j]);}
}}
return max;}
}相关文章:
)
【LeetCode-178】最长重复子串(动归)
目录 LeetCode718.最长重复子串 题目描述 解法1:动态规划 代码实现 题目链接 题目描述 给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。 示例: 输入: A: [1,2,3,2,1] B: [3,2,1,4,7] 输出&…...

1、jQuery介绍、css()、选择器、事件、动画
一、jQuery介绍? 1、什么是jQuery? 是一个JavaScript函数库 2、jQuery特点 写的少,做的多 3、jQuery的安装 直接下载引入 <script src"jquery-1.10.2.min.js"></script>通过cdn引入 <script src"https…...
ArcEngine 调用GP工具时,出现C++ R6034错误
1、Arcengine 调用GP工具时,遇到正试图在 os 加载程序锁内执行托管代码 问题 使用:把VS菜单的 调试->异常->Managed Debuggin Assistants->LoaderLock 的选中状态去掉。不会弹出该错误。 2 编译后运行EXE时,出现C R6034问题 ArcEng…...

windows下基于docker-desktop 安装 mysql 5.7
0.背景 docker-desktop v4.27.1Windows 11 22H2 docker-desktop 需要wsl的支持,一般win11新机子都默认开启了,安装docker-desktop 一路next即可.win10老版本需要自行安装开启wsl.一个小建议是,如果你的win10安装wsl时各种错误无法解决,建议升级到win11大概率解决,本人亲身经历…...

什么是Rust 语言
Rust 是一种专注于性能和内存安全的系统编程语言,其设计目标包括提供:零开销抽象、移动语义、内存安全、线程无数据竞争、类型安全和实时 gc 等功能。Rust 使用 RAII(Resource Acquisition Is Initialization)管理资源,…...

2024年四川媒体新闻发布渠道,媒体邀约资源表
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 四川有哪些媒体新闻发布渠道,媒体邀约资源表? 2024年四川媒体新闻发布渠道,媒体邀约资源表 四川本地媒体:如四川日报、华西都市报、成都商…...
14:00面试,14:07就出来了,问的问题过于变态了。。。
我从一家小公司转投到另一家公司,期待着新的工作环境和机会。然而,新公司的加班文化让我有些始料未及。虽然薪资相对较高,但长时间的工作和缺乏休息使我身心俱疲。 就在我逐渐适应这种高强度的工作节奏时,公司突然宣布了一则令人…...

利用 Python 抓取数据探索汽车市场趋势
一、引言 随着全球对环境保护意识的增强和技术的进步,新能源汽车作为一种环保、高效的交通工具,正逐渐受到人们的关注和青睐。在这个背景下,对汽车市场的数据进行分析和研究显得尤为重要。 本文将介绍如何利用 Python 编程语言,结…...
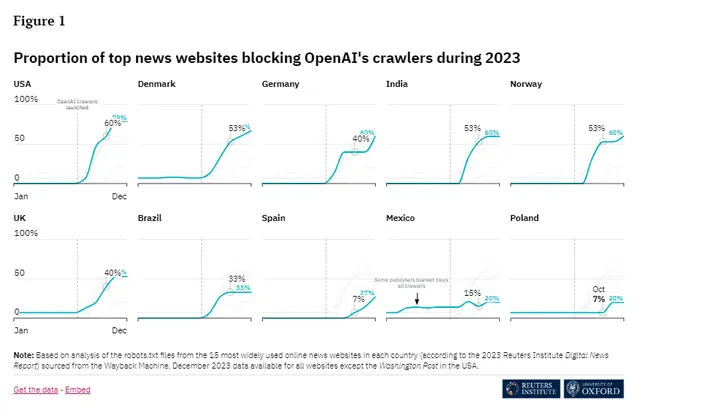
新闻网站封锁AI爬虫 AI与新闻媒体博弈继续
随着ChatGPT等新兴AI模型的兴起,它们所依赖的网络爬虫正面临来自全球主流新闻网站的大规模封锁。Richard Fletcher博士团队对十个国家主流新闻网站的统计发现,到2023年底,48%的网站屏蔽了OpenAI的爬虫,24%屏蔽了Google的爬虫。那么…...

Python Web开发记录 Day5:jQuery(JavaScript库)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 五、jQuery1、jQuery-选择器和菜单案例①快速上…...

前端-Vue3递归组件自定义Tree
需求 PS:写在前面,需求想要一个Tree 形结构展示当前的组织机构,最末层节点可以选择,层级明确。第一选择网上npm官网或者github 找找成型的东西 element-ui Tree 没有组织结构线js-tree 好看,但是适配Vue3 有点费劲&a…...

《TCP/IP详解 卷一》第12章 TCP初步介绍
目录 12.1 引言 12.1.1 ARQ和重传 12.1.2 滑动窗口 12.1.3 变量窗口:流量控制和拥塞控制 12.1.4 设置重传的超时值 12.2 TCP的引入 12.2.1 TCP服务模型 12.2.2 TCP可靠性 12.3 TCP头部和封装 12.4 总结 12.1 引言 关于TCP详细内容,原书有5个章…...
作业1-224——P1015 [NOIP1999 普及组] 回文数
题目描述 思路 首先此题为一道高精度题,然后本题按照题目意思模拟即可。我们可以开两个数组来记录高精度数字,这样方便我们处理。判断“该数组是否回文”、“c翻转存入d再做cd”可以写成两个单独的函数。然后主程序组织一下他们即可。注意好退出循环的…...
)
后端知识(理解背诵)
文章目录 🍺 来源🍺 C🍻 new 和 malloc 的区别?2🍻 delete 和 delete[] 的区别?0🍻 内存泄漏是什么?如何避免?1 🍺 计算机网络🍻 URL 输入后发生了…...
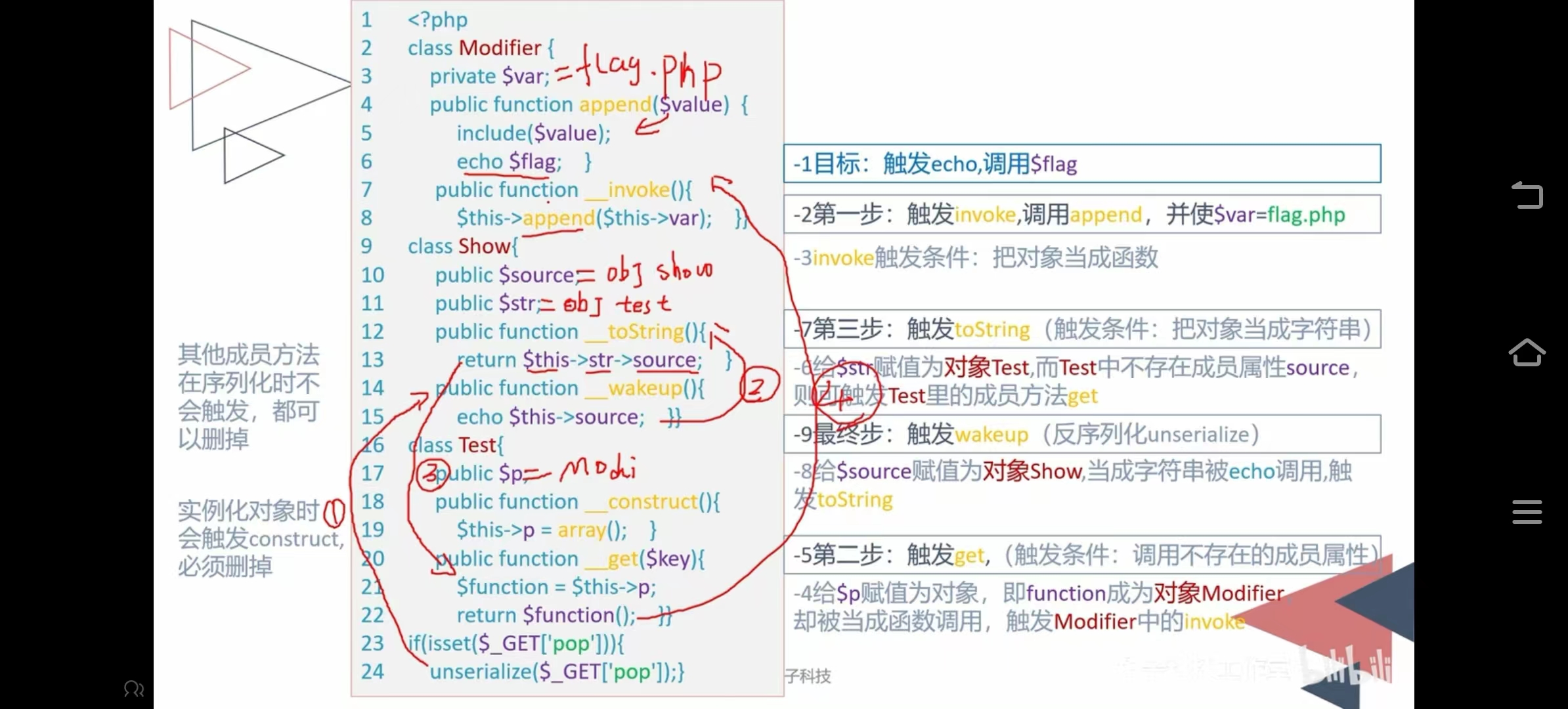
构造pop链
反序列化视频笔记 第一步:找到目标触发echo调用$flag 第二步:触发_invoke函数调用appeng函数$varflag.php(把对象当成函数) 第三步:给$p赋值为对象,即function成为对象Modifier却被当成函数调用ÿ…...
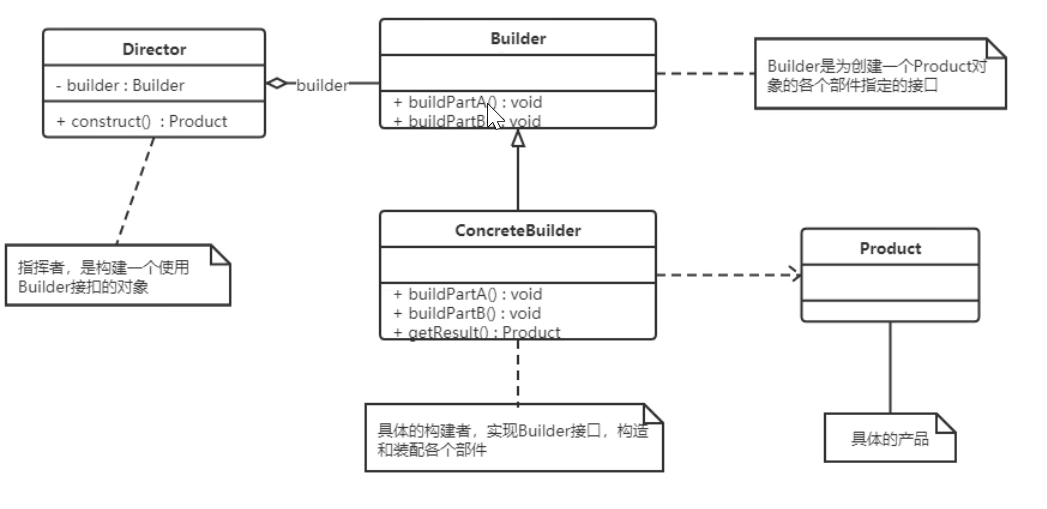
JAVA设计模式——创建型模式
JAVA设计模式——创建型模式 一、创建型模式1.单例模式(Singleton Pattern)1.1 饿汉式1.2 懒汉式1.3 双重检验锁(double check lock)(DCL)1.4 静态内部类1.5 枚举1.6 破坏单例的几种方式与解决方法1.6.1 反序列化1.6.2 反射 1.7 容器式单例1.8 ThreadLoc…...
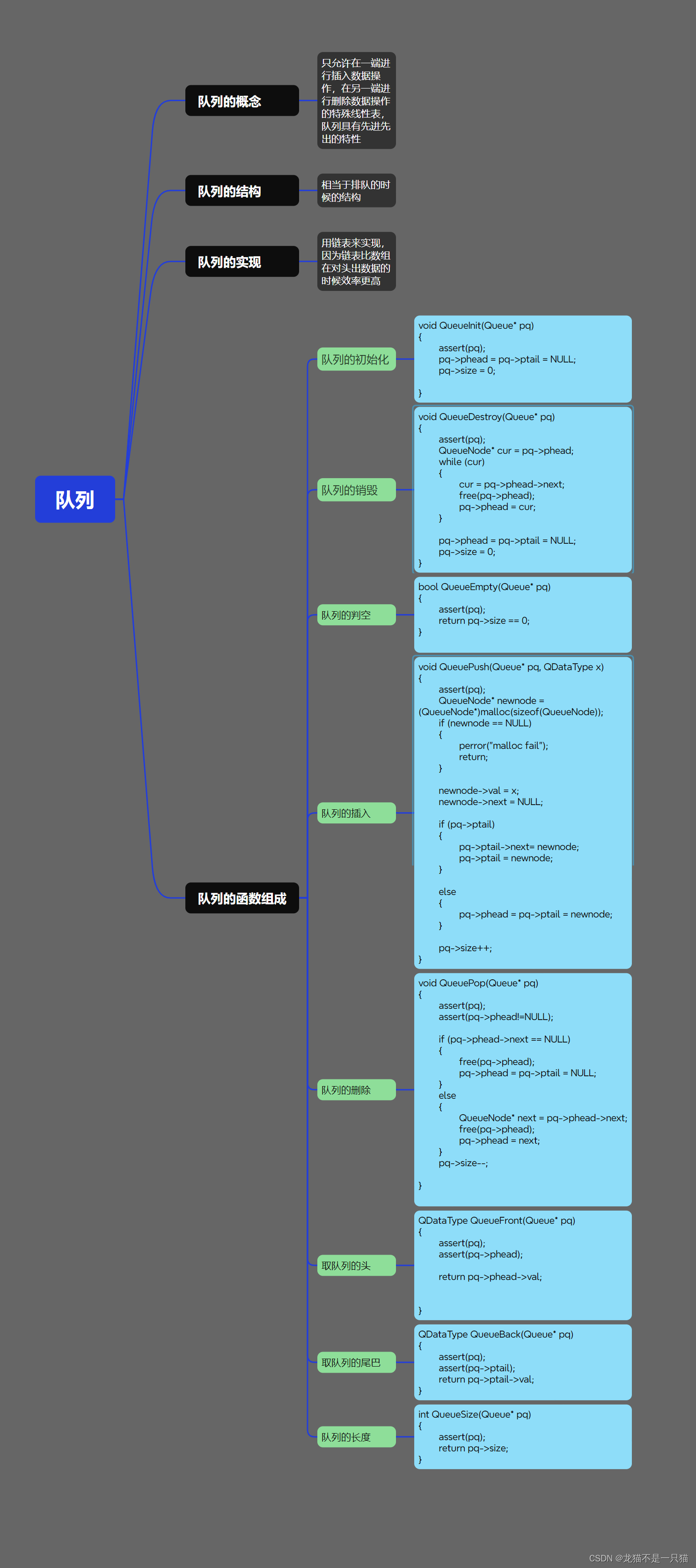
队列的结构概念和实现
文章目录 一、队列的结构和概念二、队列的实现三、队列的实现函数四、队列的思维导图 一、队列的结构和概念 什么是队列? 队列就是只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 如上图所示&#x…...

Linux系统上使用C语言创建线程
文章目录 一、使用C代码创建线程示例API 二、线程的相关知识2.1 线程 与 进程 的关系2.2 使用线程的理由 一、使用C代码创建线程 使用pthread_create函数创建线程。 示例 示例:创建一个线程,其作用就是打印线程ID和传入参数。 //demo1 #include <…...

pc端如何做自适应呢?
<!-- 默认html的font-size的大小是16px 1rem 16px --> <!-- 想要实现自适应的前提条件是 当浏览器的窗口发生变化的时候, html的font-size将会跟着发生改变 --> <!-- 实现的步骤如下 --> <!-- 1 借助flexble.js文件 --> <!-- 2 将fle…...

c语言经典测试题8
在c语言经典测试题6的第一题,大家是否想过可不可以将递归参数改为s呢?或许有的人已经试过了,但是发现好像不会有结果,其实是因为s为后置,先试用后加1,然而我们这个是在s出了函数之后才会运行加1操作&#x…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
