作业1-224——P1015 [NOIP1999 普及组] 回文数
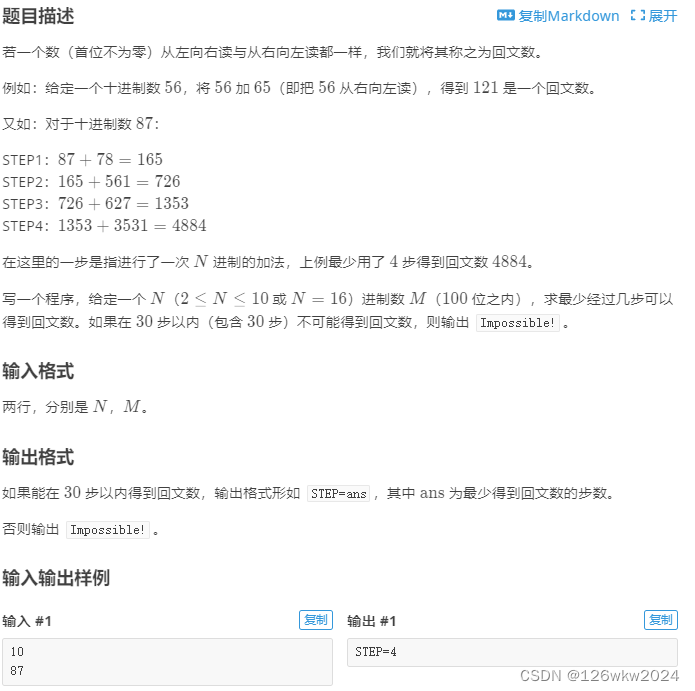
题目描述
思路
首先此题为一道高精度题,然后本题按照题目意思模拟即可。我们可以开两个数组来记录高精度数字,这样方便我们处理。判断“该数组是否回文”、“c翻转存入d再做c+d”可以写成两个单独的函数。然后主程序组织一下他们即可。注意好退出循环的条件。
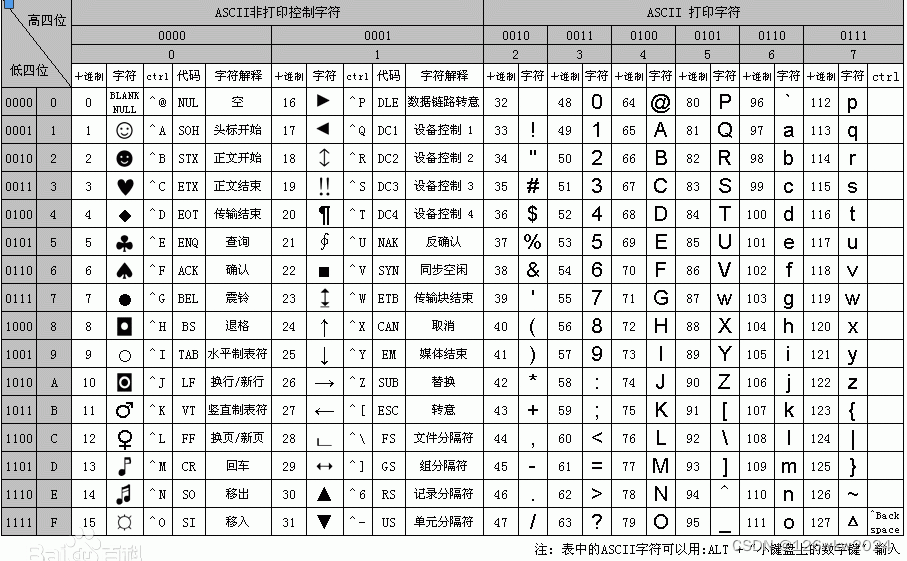
还用到ASCll码~
参考代码
#include<bits/stdc++.h>
const int S=303;
int n,a[S],l;
char c[S],d[S];
inline void add()
{
for (int i=0;i<l;++i)
d[l-i-1]=c[i];
l+=2;
for (int i=0;i<l;++i)
{
c[i]+=d[i];
if (c[i]>=n) c[i+1]++,c[i]-=n;
}
while (!c[l-1]) --l;
}
inline bool pd()
{
for (int i=0;i<l;++i)
if (c[i]!=c[l-1-i]) return false;
return true;
}
int main()
{
scanf("%d",&n);
scanf("%s",s);
l=strlen(c);
for (int i=0;i<l;++i)
{
if (c[i]>='0' && c[i]<='9') c[i]-='0';
else c[i]=c[i]-"A"+10;
}
int step=0;
while (!pd())
{
++step;
if (step>30) break;
add();
}
if (step<=30) printf("STEP=%d\n",step);
else puts("Impossible!");
return 0;
}
简化代码
#include <bits/stdc++.h>
const int S=303;
int n,a[S],l;
char c[S],d[S];
void add()
{
for (int i=0;i<l;++i)
d[l-i-1]=c[i];
l+=2;
for (int i=0;i<l;++i)
{
c[i]+=d[i];
if (c[i]>=n) c[i+1]++;c[i]-=n;
}
while (!c[l-1]) --l;
bool pd()
{
for (int i=0;i<l;++i)
if (c[i]!=c[l-1-i]) return false;
return true;
}
int main()
{
scanf("%d",&n);
scanf("%s",s);
l=strlen(c);
for (int i=0;i<l;++i)
{
if (c[i]>='0' && c[i]<='9') c[i]-='0';
else c[i]=c[i]-55;
}
int step=0;
while (!pd())
{
++step;
if (step>30) break;
add();
}
if (step<=30) printf("STEP=%d\n",step);
else puts("Impossible!");
return 0;
}-->inline可以不要,A可以转换为ASCll数字;
学会的知识
代码可以简化,带字符可以转换为ASCll数字;
相关文章:

作业1-224——P1015 [NOIP1999 普及组] 回文数
题目描述 思路 首先此题为一道高精度题,然后本题按照题目意思模拟即可。我们可以开两个数组来记录高精度数字,这样方便我们处理。判断“该数组是否回文”、“c翻转存入d再做cd”可以写成两个单独的函数。然后主程序组织一下他们即可。注意好退出循环的…...
)
后端知识(理解背诵)
文章目录 🍺 来源🍺 C🍻 new 和 malloc 的区别?2🍻 delete 和 delete[] 的区别?0🍻 内存泄漏是什么?如何避免?1 🍺 计算机网络🍻 URL 输入后发生了…...
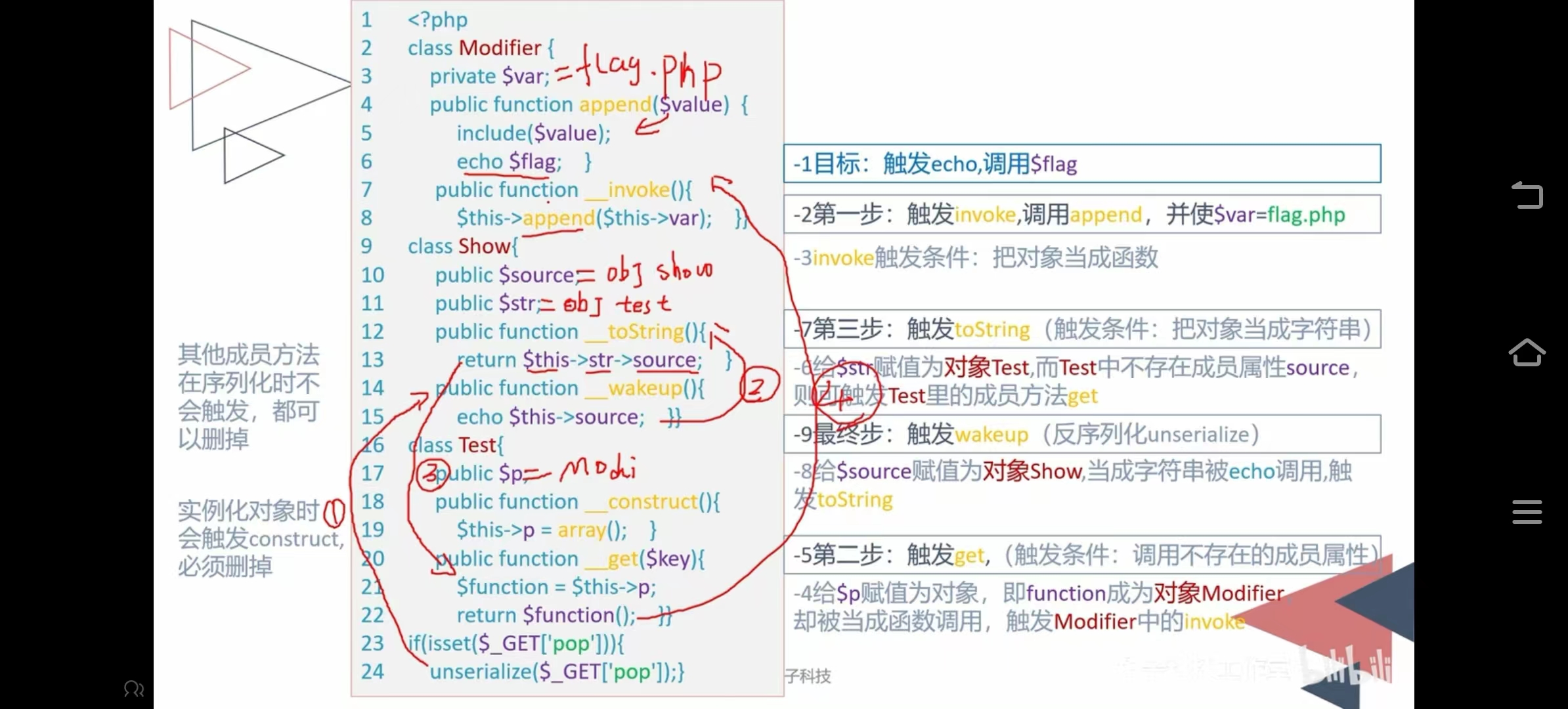
构造pop链
反序列化视频笔记 第一步:找到目标触发echo调用$flag 第二步:触发_invoke函数调用appeng函数$varflag.php(把对象当成函数) 第三步:给$p赋值为对象,即function成为对象Modifier却被当成函数调用ÿ…...
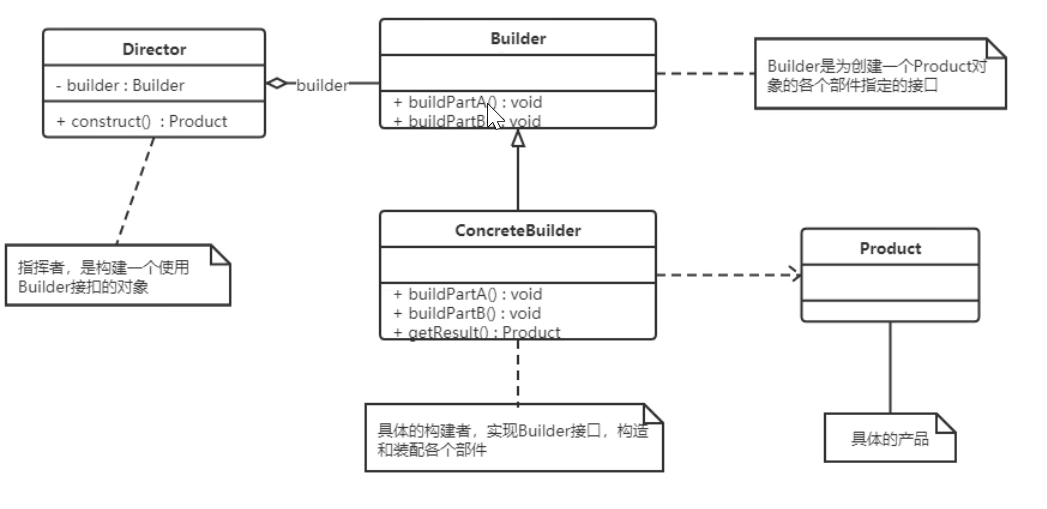
JAVA设计模式——创建型模式
JAVA设计模式——创建型模式 一、创建型模式1.单例模式(Singleton Pattern)1.1 饿汉式1.2 懒汉式1.3 双重检验锁(double check lock)(DCL)1.4 静态内部类1.5 枚举1.6 破坏单例的几种方式与解决方法1.6.1 反序列化1.6.2 反射 1.7 容器式单例1.8 ThreadLoc…...
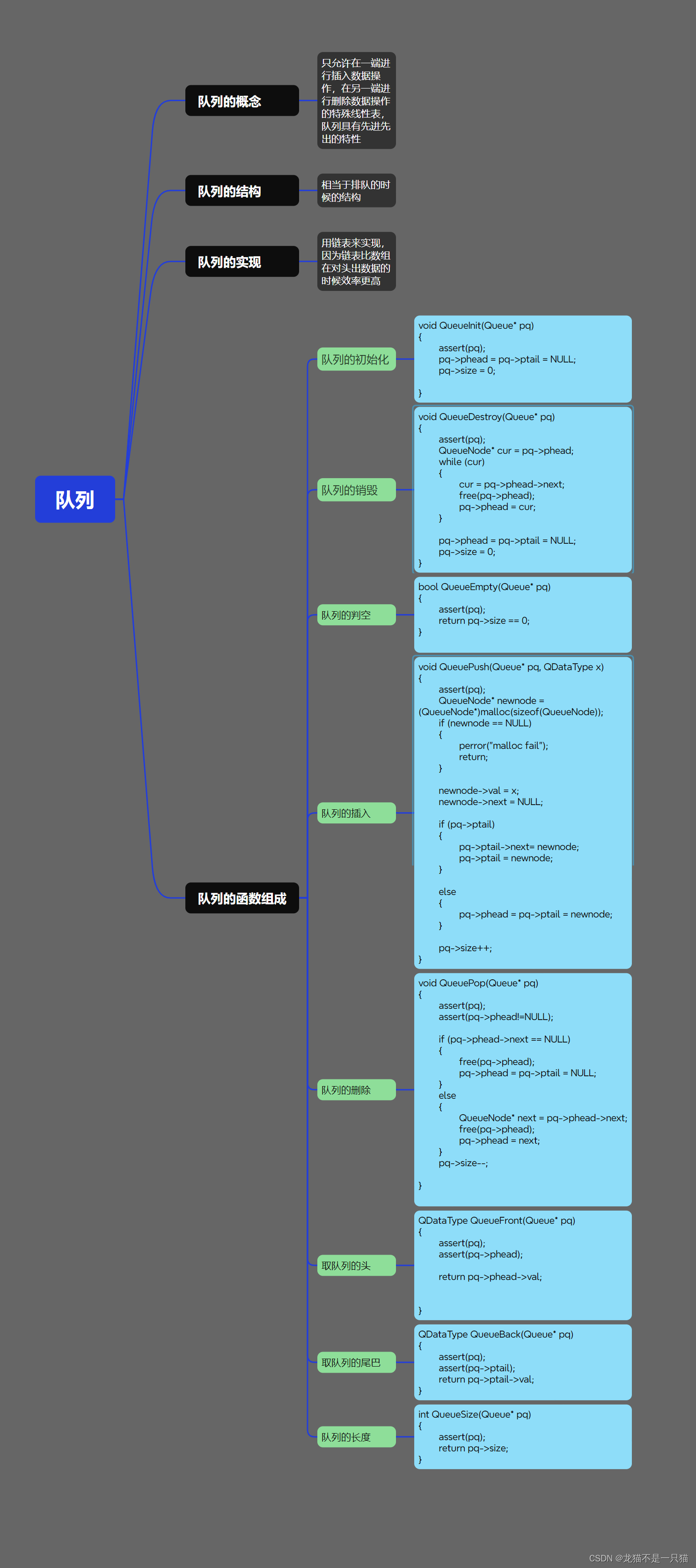
队列的结构概念和实现
文章目录 一、队列的结构和概念二、队列的实现三、队列的实现函数四、队列的思维导图 一、队列的结构和概念 什么是队列? 队列就是只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 如上图所示&#x…...

Linux系统上使用C语言创建线程
文章目录 一、使用C代码创建线程示例API 二、线程的相关知识2.1 线程 与 进程 的关系2.2 使用线程的理由 一、使用C代码创建线程 使用pthread_create函数创建线程。 示例 示例:创建一个线程,其作用就是打印线程ID和传入参数。 //demo1 #include <…...

pc端如何做自适应呢?
<!-- 默认html的font-size的大小是16px 1rem 16px --> <!-- 想要实现自适应的前提条件是 当浏览器的窗口发生变化的时候, html的font-size将会跟着发生改变 --> <!-- 实现的步骤如下 --> <!-- 1 借助flexble.js文件 --> <!-- 2 将fle…...

c语言经典测试题8
在c语言经典测试题6的第一题,大家是否想过可不可以将递归参数改为s呢?或许有的人已经试过了,但是发现好像不会有结果,其实是因为s为后置,先试用后加1,然而我们这个是在s出了函数之后才会运行加1操作&#x…...

解决GitHub无法访问的问题:手动修改hosts文件与使用SwitchHosts工具
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua,在这里我会分享我的知识和经验。&#x…...
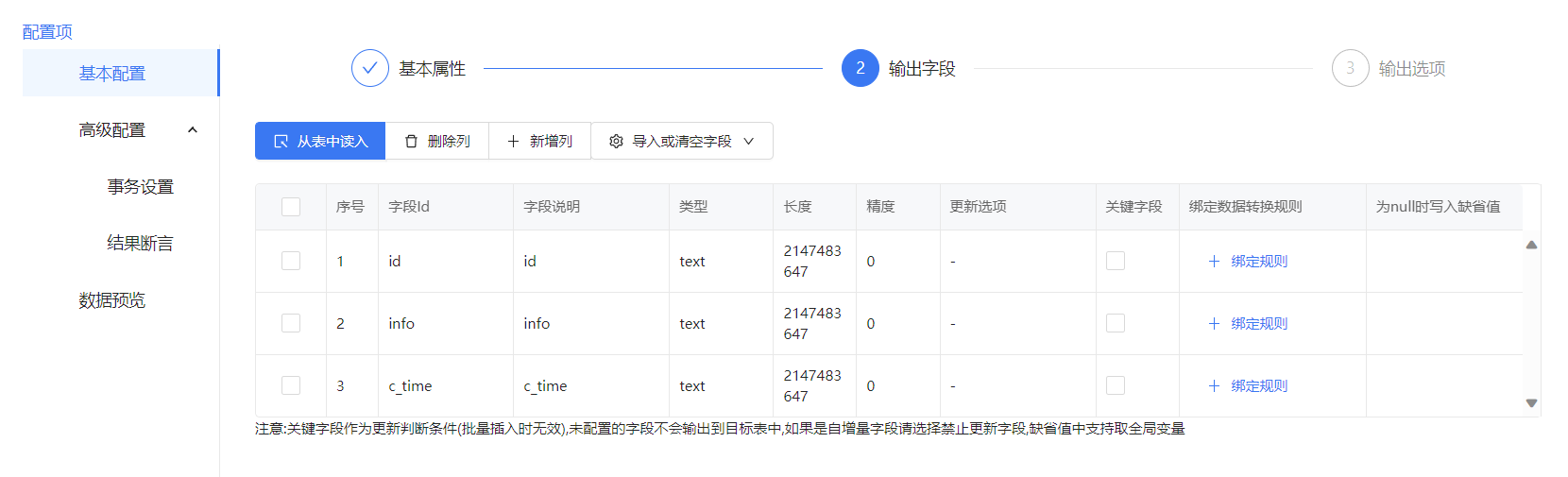
ETL数据仓库的使用方式
一、ETL的过程 在 ETL 过程中,数据从源系统中抽取(Extract),经过各种转换(Transform)操作,最后加载(Load)到目标数据仓库中。以下是 ETL 数仓流程的基本步骤:…...

POST参数里加号+变成空格的问题处理
今天遇到个这样的问题,从前端传到后端的加密报文,里面包含了号,但在后端日志输出看出,变成空格。这个是由于经过RSA加密后引起的 解决办法: 1.前端转码:使用encodeURIComponent对参数进行转码 2.后端解码…...

【华为面试基础题】检查是否存在满足条件的数字组合
描述 给定一个正整数数组检查数组中是否存在满足规则的数组组合 规则: AB2C 输入描述: 第一行输出数组的元素个数,接下来一行输出所有数组元素,用空格隔开 输出描述: 如果存在满足要求的数 在同一行里依次输出 规则…...
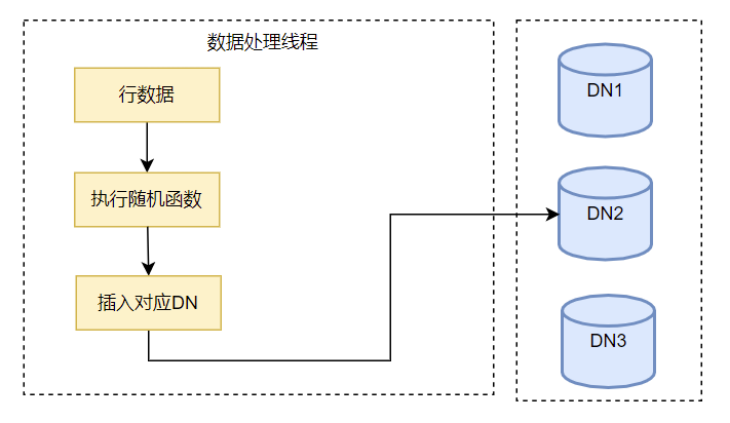
亚信安慧AntDB数据并行加载工具的实现(一)
1.概述 数据加载速度是评判数据库性能的重要指标,能否提高数据加载速度,对文件数据进行并行解析,直接影响数据库运维管理效率。基于此,AntDB分布式数据库提供了两种数据加载方式: 一是类似于PostgreSQL的Copy命令&am…...

面经 | Java创建线程的三种方式
利用JUC包创建线程的三种方式: 通过继承Thread类创建线程类实现Runnable接口创建线程类通过Callable和Future接口创建线程 继承Thread类创建线程 class Thread1 extends Thread {Overridepublic void run() {System.out.println("启动线程1");} }实现R…...

【计算机网络】五种IO模型与IO多路转接之select
文章目录 一、五种IO模型二、非阻塞IO1.fcntl2.实现函数SetNoBlock3.轮询方式读取标准输入 三、I/O多路转接之select1.初识select2.select函数原型3.socket就绪条件4.select的特点5.select缺点6.select使用案例--只读取数据的server服务器1.err.hpp2.log.hpp3.sock.hpp4.select…...

通过一篇文章让你了解数据结构和算法的重要性
通过一篇文章让你了解数据结构和算法的重要性 前言一、 什么是数据结构?二、什么是算法?三、数据结构和算法的重要性在校园招聘的笔试中:在校园招聘的面试中:在未来的工作中: 四、如何学好数据结构和算法4.1 死磕代码&…...

python代码优化学习
代码优化对比: 优化前: # 登录系统 xxljob_login() start_time time.time() # 循环处理需要补数的数据 for item in authId_lists: preSettleInfoHandler(item) count 1 print("运行了第" str(count) "个") …...

C#,数值计算,求解微分方程的吉尔(Gear)四阶方法与源代码
1 微分方程 微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。 微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛,可以解决许多与导数…...

2024年新提出的算法|LEA爱情进化算法(Love Evolution Algorithm)
Love Evolution Algorithm: a stimulus–value–role theory-inspired evolutionary algorithm for global optimization 爱情进化算法Love Evolution Algorithm,LEA,于2024年2月发表在中科院3区SCI期刊 The Journal of Supercomputing。 1、简介 本文提…...

javaWeb个人学习02
会话技术 会话: 用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断开连接,会话结束.在一次会话中包含多次请求和响应 会话跟踪: 一种维护浏览器状态的方法,服务器需要识别多次请求是否来自于同一个浏览器,以便在同一次会话的多次请求之间共享数据 会话跟踪方案: …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
