MATLAB环境下脑电信号EEG的谱分析
脑电信号一直伴随着人类的生命,脑电波是脑神经细胞发生新陈代谢、离子交换时细胞群兴奋突触电位总和,脑电信号的节律性则和丘脑相关,含有丰富的大脑活动信息。通常我们所接触的脑电图都是头皮脑电图,在有些特殊场合还需要皮下部位的脑电图,脑电信号主要有以下几个特点:
(1)脑电信号只有50pV左右,所以非常的微弱,通常头皮脑电信号,超过100pV的可以认作是噪声。脑电信号按照波幅值可以分为高、中、低三种:低波幅值小于25pV;中波幅值大于25pV小于50pV;高波幅值大于50pV。
(2)具有随机性及非平稳性。脑电信号被影响的因素很多,但规律通常都没有被识别,通常来说,脑电信号的规律从大量的数据统计、大量的技术处理检测、识别和估计结果中显示,并且生命体对外界的自适应力,以及生理因素的作用都对脑电信号产生了影响,所以脑电信号具有着随机性和非平稳性,并且一直随着时间在变化。
(3)具有非高斯、非线性的特征。生物组织自适应和生理机使得人体脑电的信号有非线性的特性,当前信号处理通常通过线性系统分析基础上进行,所以在分析方法上如何最小地去减小非线性误差在脑电信号的处理上也应该要考虑。
(4)脑电信号容易受到诸多的背景噪声干扰。影响脑电波的因素还有很多。比如人的年龄,当人在50岁以后,慢波又可以逐渐回升,还有着不同程度的基频慢波。脑波还更易受到意识、情绪以及思维状态等因素的影响。
脑电波在病理的状态下的形态也经常会出现一些异常瞬态波。尖波周期范围是在80~200ms,其波形快速上升、缓慢下降,类似于三角波,病症常见于癫痫。棘波多见于局限性的癫痫,而棘慢综合波是通过棘波和慢波所构成的复合波。
鉴于此,本项目采用谱分析方法,对两个来源(PhysioNet数据库和自测数据库)的脑电信号进行了研究,目标是应用不同的时频谱分析技术评估相应的结果。算法程序运行环境为MATLAB R2021b,执行EEG信号的谱分析,也可迁移至金融时间序列,地震信号,机械振动信号,语音信号,声信号等一维时间序列信号。
部分代码如下:
%EEG Signal Spectral Analysis
%Load data & Initialize params
%Sleep dataset
clear;
[x, Fs, Start_date, Start_time, Label, Dimension, Coef, Nmb_chans,N] = readedf_EX1('sc4002e0.rec',0,0,360);
windows = int16([128 256 512]);
overlaps = double([0 0.25 0.50 0.75]);
dft_points = [64 128 256 512 1024];
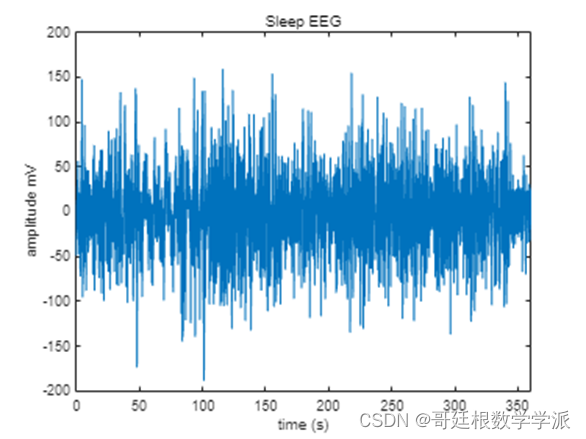
Signal overview
figure
time = linspace(0,length(x)/Fs, length(x));
plot(time,x)
axis('normal')
title('Sleep EEG')
xlim([0 length(time)/Fs])
xlabel('time (s)')
ylabel('amplitude mV')1. PSD params experiment1.1 Window size
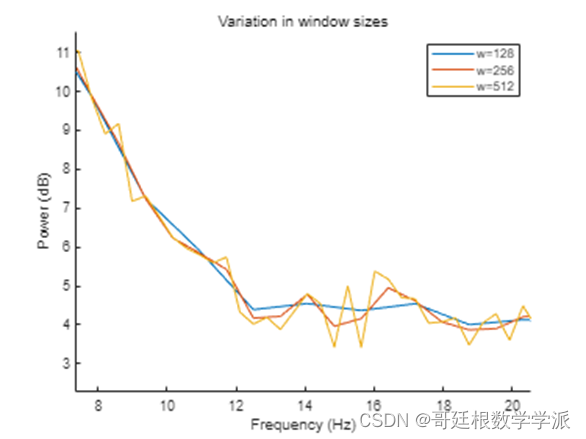
figure
hold on
for i=1:length(windows)[pxx, f] = pwelch(x,windows(i),overlaps(3)*windows(i),dft_points(i),100);plot(f, pow2db(pxx))
end
legend(sprintf('w=%d', windows(1)), ...sprintf('w=%d',windows(2)), ...sprintf('w=%d', windows(3)))
xlabel('')
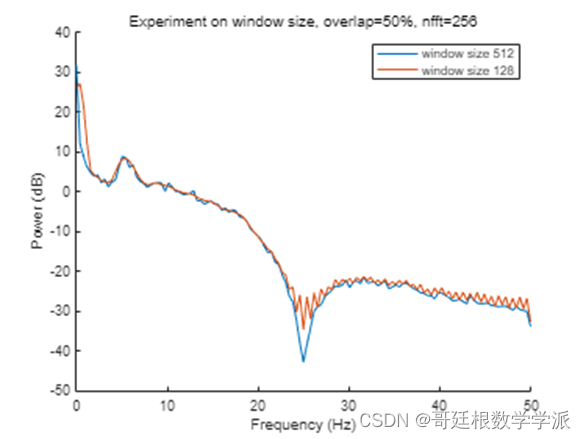
title('Variation in window sizes')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
hold off
% Better visualization for comparision
xlim([7.37 20.53])
ylim([2.30 11.52])1.2 Overlap
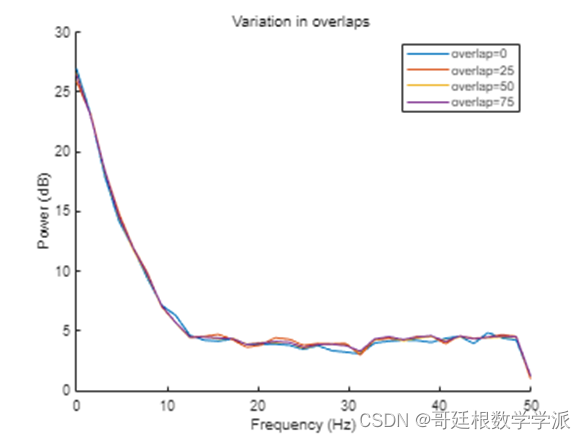
figure
hold on
noverlaps = overlaps .* 128;
for i=1:length(noverlaps)[pxx, f] = pwelch(x, windows(1), noverlaps(floor(i)), dft_points(1), 100);plot(f, pow2db(pxx),'LineWidth',1)
end
legend(sprintf('overlap=%d %', overlaps(1)*100), ...sprintf('overlap=%d %', overlaps(2)*100), ...sprintf('overlap=%d %', overlaps(3)*100),...sprintf('overlap=%d %', overlaps(4)*100))
xlabel('')
title('Variation in overlaps ')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
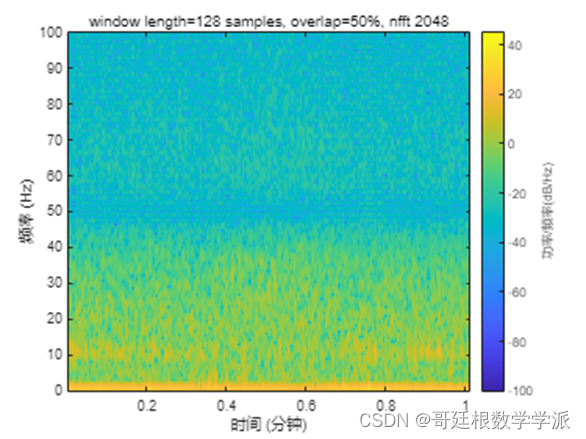
hold off1.3 Number of DFT points
figure
hold on
for i=1:length(dft_points)[pxx, f] = pwelch(x,windows(1),overlaps(2)*windows(1),dft_points(i),100);plot(f, pow2db(pxx))
end
legend(sprintf('nfft=%d', dft_points(1)), ...sprintf('nfft=%d',dft_points(2)), ...sprintf('nfft=%d',dft_points(3)), ...sprintf('nfft=%d',dft_points(4)), ...sprintf('nfft=%d', dft_points(5)))
xlabel('')
title('Variation in number of DFT points')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
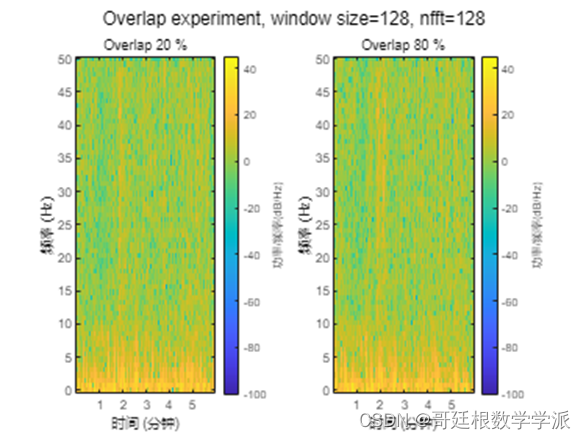
hold off2. Spectrogram params experimentspec_w_1 = 128;
spec_w_2 = 512;
spec_o_1 = 0.5;
spec_o_2 = 0.8;
spec_o_3 = 0.2;
spec_nfft_1 = 128;
spec_nfft_2 = 1024;2.1 Window size
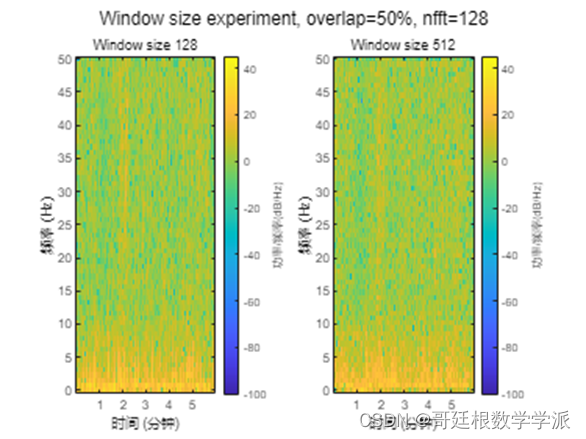
Small window size results in high detail frequecy representation.
Large window size results in blocky-looking frequecy representation.
figure;
subplot(1,2,1);
spectrogram(x,spec_w_1,64,128,Fs,'yaxis');
set(gca, 'Clim', [-100 45]);
title(sprintf('Window size %d', spec_w_1))subplot(1,2,2);
spectrogram(x,spec_w_2, spec_o_1 * spec_w_2,128,Fs,'yaxis');
set(gca, 'Clim', [-100 45]);
title(sprintf('Window size %d', spec_w_2))sgtitle(sprintf('Window size experiment, overlap=%d%%, nfft=%d', spec_o_1*100, spec_nfft_1));出图如下:



工学博士,担任《Mechanical System and Signal Processing》审稿专家,担任
《中国电机工程学报》优秀审稿专家,《控制与决策》,《系统工程与电子技术》,《电力系统保护与控制》,《宇航学报》等EI期刊审稿专家。
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
相关文章:

MATLAB环境下脑电信号EEG的谱分析
脑电信号一直伴随着人类的生命,脑电波是脑神经细胞发生新陈代谢、离子交换时细胞群兴奋突触电位总和,脑电信号的节律性则和丘脑相关,含有丰富的大脑活动信息。通常我们所接触的脑电图都是头皮脑电图,在有些特殊场合还需要皮下部位…...
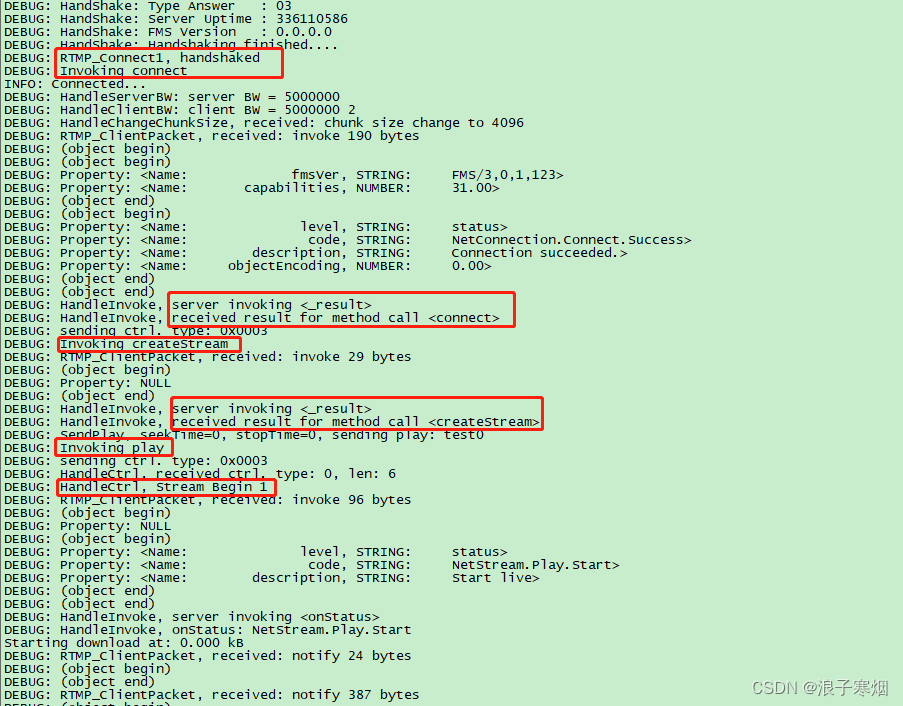
librtmp源码分析
阅读了librtmp的源码,简单记录下。 首先补充下AMF格式基本知识 1 AMF格式 AMF是Action Message Format(动作消息格式)的简写,它是一种二进制的数据格式。它的设计是为了把actionscript里面的数据(包括Object, Array, Boolean, Number等)序列化成二进制…...

CCDP.00.问老师问题前你首先需要做的事情
一、一定要按老师要求做好快照!!!!! 1、在关键节点处,比如做完Part1后,关机状态下做快照。 2、在做没把握的操作前先做快照(这个可以在开机状态下做快照,但推荐关机状态…...

「算法」常见位运算总结
位运算符 异或 按位异或可以实现无进位相加,所谓无进位相加,就是在不考虑进位的情况下将两个数相加(后面有道题需要用到这种操作) 异或的运算律 ①a ^ 0 a ②a ^ a 0 ③a ^ b ^ c a ^ ( b ^ c ) 有符号右移>> 将一个…...
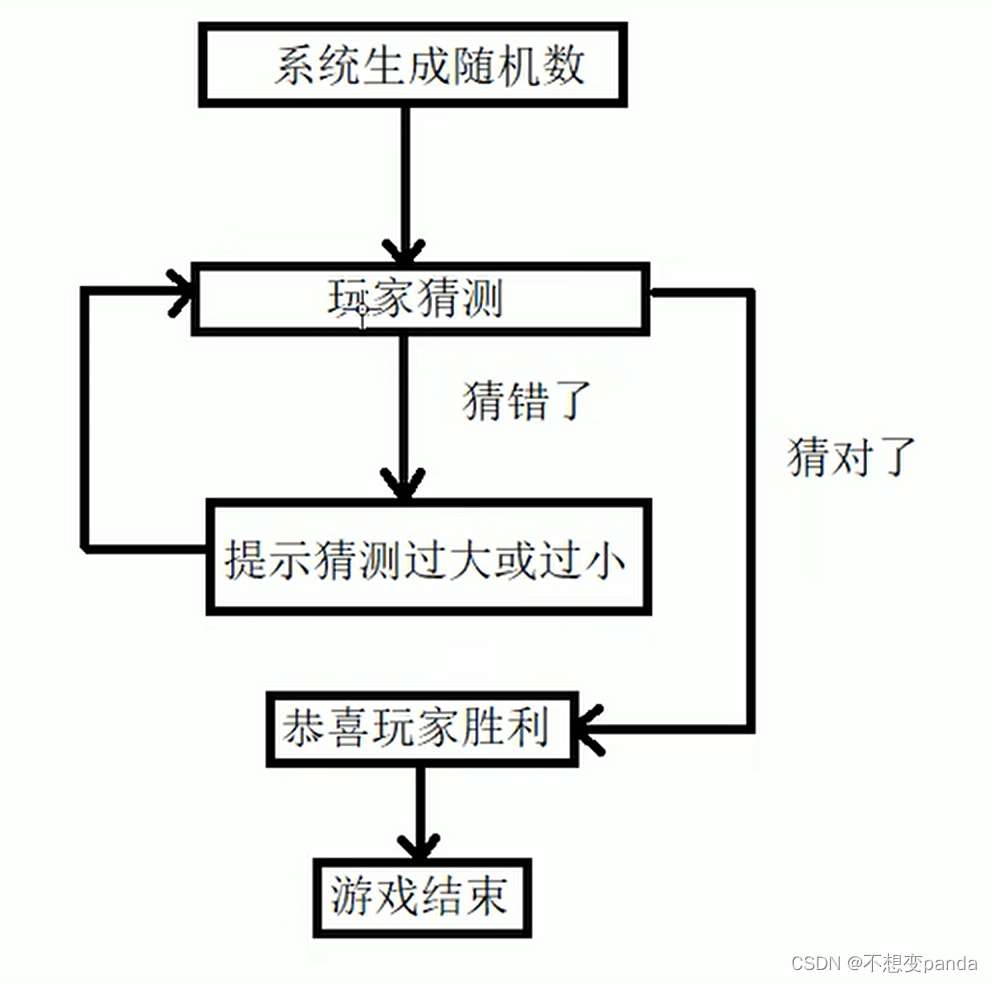
【C++初识】语句
文章目录 1.注释 变量 常量 关键字 标识符命名规则 数据类型 sizeof关键字 数据的输入 运算符2.程序流程结构2.1选择结构2.2循环结构2.21while{循环条件}{循环语句};//满足循环条件,执行循环语句2.22do{循环语句}while{循环条件};//do....whi…...

Python线性代数傅里叶分析和动态系统模拟分析之一
要点 Python向量数值计算、可视化,线性独立性和子空间。了解欧几里德距离、余弦相似度和皮尔逊相关性应用案例:Python数值计算文档相似度时间序列和特征检测示例:Python信号处理边缘检测器, K均值示例:随机簇质心分布Python傅里叶…...
)
mysql插入GEOMETRY相关字段类型(point,linestring等)
一、问题 向mysql中插入point,linestring等相关空间坐标字段,出现报错: 1416 - Cannot get geometry object from data you send to the GEOMETRY field要插入的数据:...

vue3学习 【5】watch的使用
什么是watch 当我们需要根据一个数据的变化来进行一些操作的时候我们需要使用侦听器,它能够在响应式数据发生变化的时候触发提供的回调函数 基础侦听 watch 可以侦听不同的数据源。例如: ref计算属性响应式对象getter函数多个数据源组层的数据 cons…...
PyTorch深度学习快速入门
PyTorch深度学习快速入门 1.PyTorch环境配置及安装2.python编辑器的选择、安装、配置(pycharm、JupyTer安装)3.为什么torch.cuda.is_available()返回false4.python学习中两大法宝函数(也可用在pytorch)5.pycharm和jupyter…...
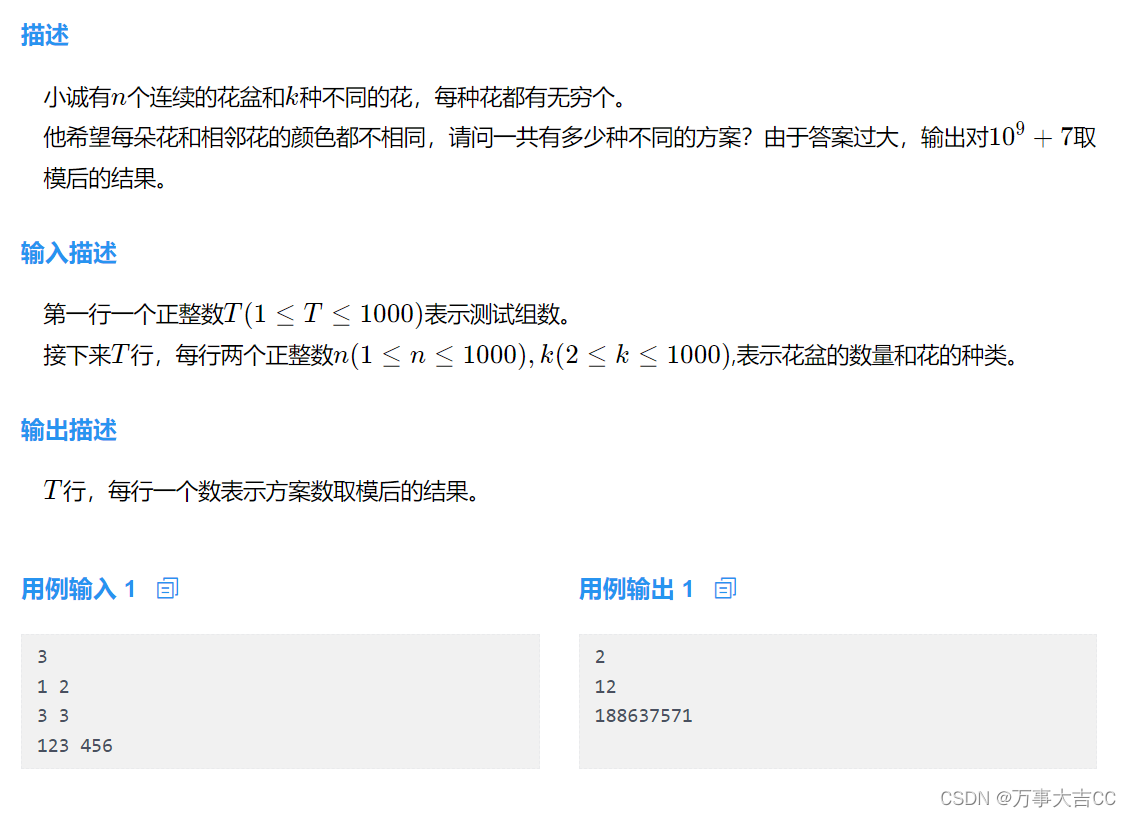
种花
分情况: 第一盆k种选择,之后全部k-1种选择 每次相乘结果对1e97取模 #include <iostream> #include <vector> #include <algorithm> using namespace std; #define endl \n const int N 1e9 7;int main() {ios::sync_with_stdio(f…...
)
Android Shadow插件化框架分析与集成(二)
本文索引 前言插件打包后如何交给宿主使用?宿主加载插件代码分析全局初始化操作加载插件activity测试过程中遇到的问题报错 1 :报错2:报错3 :二次开发支持多插件、多进程功能mPpsController 的构造方式mPluginLoader的构造方式多插件如何改造前言...

Go 与 Rust:导航编程语言景观
在当今构建软件时,开发者在编程语言上有着丰富的选择。两种脱颖而出的语言是 Go 和 Rust - 都很强大但却截然不同。本文将从各种因素比较这两种语言,以帮助您确定哪种更适合您的需求。 我们将权衡它们在并发、安全性、速度、互操作性等方面的方法。我们将…...

包管理工具之npm也慌了?
起因 因为npm的种种问题,我很早就换成了pnpm和yarn(但是其实npm也在使用),已经很久没有关注npm的功能更新了。最近无意间进入Node18版本的安装目录,发现其除了常规的node,npm等默认安装了一个新的包corepack,这个就是今天我要分享的东西了。 注: 我因为18版本的node上…...
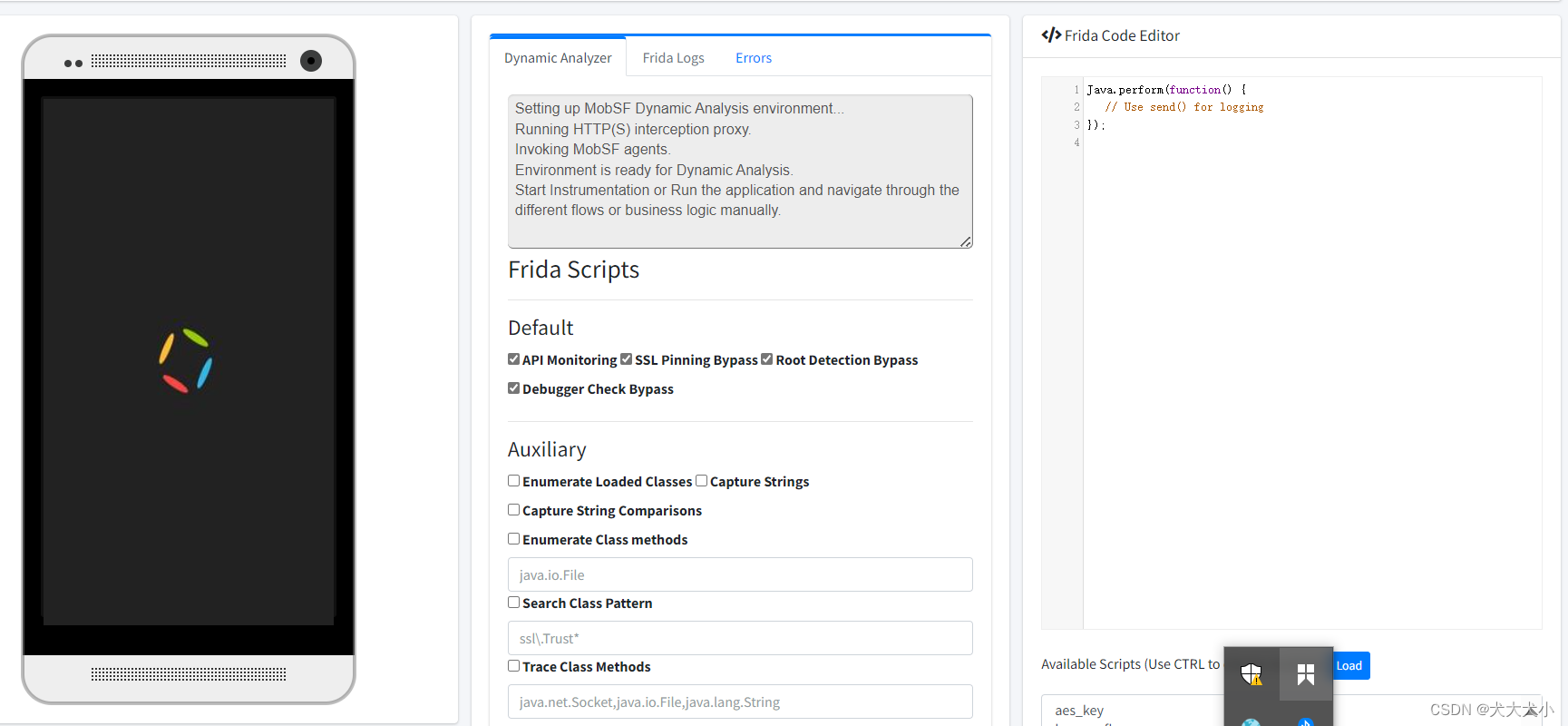
mobile app 安全扫描工具MobSF了解下
可以干啥: static 静态分析 dynamic 动态分析 可以用来渗透了 如何docker安装 docker image 下载地址https://hub.docker.com/r/opensecurity/mobile-security-framework-mobsf/ setup 两行即可 1 docker pull opensecurity/mobile-security-framework-mobsf…...

Gophish+EwoMail 自建钓鱼服务器
GophishEwoMail 自建钓鱼服务器 文章目录 GophishEwoMail 自建钓鱼服务器1.前提准备2.搭建EwoMail邮件服务器1)Centos7 防火墙操作2)设置主机名3)host配置4)安装EwoMail5)获取DKIM6)端口服务介绍7ÿ…...

Dockerfile(5) - CMD 指令详解
CMD 指定容器默认执行的命令 # exec 形式,推荐 CMD ["executable","param1","param2"] CMD ["可执行命令", "参数1", "参数2"...]# 作为ENTRYPOINT的默认参数 CMD ["param1","param…...
使用 Gradle 版本目录进行依赖管理 - Android
/ 前言 / 在软件开发中,依赖管理是一个至关重要的方面。合理的依赖版本控制有助于确保项目的稳定性、安全性和可维护性。 Gradle版本目录(Version Catalogs)是 Gradle 构建工具的一个强大功能,它为项目提供了一种集中管理依赖…...
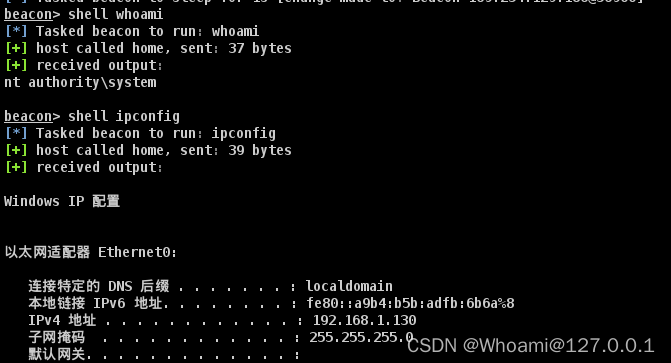
CS_上线三层跨网段机器(完整过程还原)
以前讲过用cs_smb_beacon上线不出网机器,但是真实的网络拓扑肯定不止这么一层的网络! 所以我就来搭建一个复杂一点的网络环境!! 当然了,这三台电脑之间都是不同的网段,(但是同属于一个域环境&a…...

crpto 的AES算法解密为空
1. 需求 对用户密码加密存入数据库,修改密码时取出密码在前端解密(保证密码前后端传输过程中为密文)。 文档地址:CryptoJS - CryptoJS (gitbook.io) 2. 原代码 2.1 加密 var userpass "123456"; var aseKey &quo…...

13.网络游戏逆向分析与漏洞攻防-网络通信数据包分析工具-如果没有工具就创造工具
内容参考于: 易道云信息技术研究院VIP课 上一个内容 :12.游戏网络通信存在的问题 现在把游戏网络的架构看了一个小小的大概,可以用它的接口发数据接收数据了,如果真正想用它这一套东西,真正核心不在于它的接口而在于…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
