【二分查找】分巧克力、机器人跳跃、数的范围
Halo,这里是Ppeua。平时主要更新C语言,C++,数据结构算法......感兴趣就关注我吧!你定不会失望。
🌈个人主页:主页链接
🌈算法专栏:专栏链接
我会一直往里填充内容哒!
🌈LeetCode专栏:专栏链接
目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目,也会当天做完发出
🌈代码仓库:Gitee链接
🌈点击关注=收获更多优质内容🌈
开始准备蓝桥杯啦!这是计划的一部分,每天都会更新一个专题的内容,内容参考自acwing蓝桥杯辅导课,有兴趣的uu们也可以自行观看
二分查找模板在前几篇文章中有讲过 二分查找详解
题目:数的范围
给定一个按照升序排列的长度为 n的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k的起始位置和终止位置(位置从 00 开始计数)。
如果数组中不存在该元素,则返回
-1 -1。输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n个整数(均在 1∼100001∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回
-1 -1。数据范围
1≤n≤100000
1≤q≤100001
1≤k≤100001输入样例:
6 3 1 2 2 3 3 4 3 4 5输出样例:
3 4 5 5 -1 -1
白话讲解:
非常经典的二分模板 ,通过前面的学习,我们知道二分查找有一个范围的问题,即是mid>= 还是mid>,也就是开闭区间的问题,这题完美诠释了这个特性
代码实现:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int q[N];
int main()
{scanf("%d%d",&n/*正数组长度*/,&m/*查询个数*/);for(int i=0;i<n;i++){scanf("%d",&q[i]);}while(m--){int x=0;scanf("%d",&x);int left=0,right=n-1;while(left<right){int mid=(left+right)>>1;if(q[mid]>=x)right=mid;else left=mid+1;}if(q[left]!=x)cout<<"-1 "<<"-1 "<<endl;else{cout<<left<<" ";int left=0,right=n-1;while(left<right){int mid=(left+right+1)>>1;if(q[mid]<=x)left=mid;else right=mid-1;}cout<<left<<endl;}}return 0;
}题目:机器人跳跃问题
机器人正在玩一个古老的基于 DOS 的游戏。
游戏中有 N+1 座建筑——从 00 到 N 编号,从左到右排列。
编号为 00 的建筑高度为 00 个单位,编号为 i 的建筑高度为 H(i) 个单位。
起初,机器人在编号为 00 的建筑处。
每一步,它跳到下一个(右边)建筑。
假设机器人在第 k个建筑,且它现在的能量值是 E,下一步它将跳到第 k+1 个建筑。
如果 H(k+1)>E,那么机器人就失去 H(k+1)−E的能量值,否则它将得到 E−H(k+1)的能量值。
游戏目标是到达第 N个建筑,在这个过程中能量值不能为负数个单位。
现在的问题是机器人至少以多少能量值开始游戏,才可以保证成功完成游戏?
输入格式
第一行输入整数 N。
第二行是 N个空格分隔的整数,H(1),H(2),…,H(N) 代表建筑物的高度。
输出格式
输出一个整数,表示所需的最少单位的初始能量值上取整后的结果。
数据范围
1≤N,H(i)≤1e5
输入样例1:
5 3 4 3 2 4输出样例1:
4输入样例2:
3 4 4 4输出样例2:
4输入样例3:
3 1 6 4输出样例3:
3
白话讲解:
也就是有一个机器人要进行平台跳跃
若平台比他现在的位置高,则需要扣除h(i)-E的能量,若他比平台高,则能获得E-h(i)的能量,要求跳跃中能量不能为负
题解:
分析两个扣除能量的规则就可以发现,不论高低与否,能量E=2E-h(i) ,也就是能量一直都是这样改变的,判断是否能用二分来搜寻答案最重要的就是判定其是否满足递增的条件(必要不充分),
当找到一个满足条件的E之后,大于E的情况下是都能跳跃过去.所以我们用二分来做.
int的数据范围最大为1e9,而观察这题题设范围,当h(i)足够小的时候,E=2E,有可能爆int,所以我们推断,当E=h(i)max时,此时表达式为E=E+h(i)max-h(i) h(i)无限小,即可忽略不计,所以当E=h(i)max时,即可表示其可跳跃过之后所有的格子.
也可以理解为,当我跳到最高点时,之后都是在增加能量,而不是减少,所以即可判定一定能跳过
另外,刚刚说过了>=E的条件都满足题解,所以这里的二分为left=mid+1 right=mid
不懂我在说什么的uu可以回顾下二分
check函数为:模拟跳跃每一次
代码实现:
#include<iostream>
#include<stdio.h>
using namespace std;
const int N=100010;
long n=0,h[N];
bool check(int e)
{for(int i=1;i<=n;i++){e=2*e-h[i];if(e>=1e5)return true;if(e<0)return false;}return true;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&h[i]);}int l=0,r=1e5;while(l<r){int mid=l+r>>1;if(check(mid))r=mid;else l=mid+1;}printf("%d\n",r);}题目:分巧克力蛋糕
儿童节那天有 K 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。为了公平起见,
小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足:
形状是正方形,边长是整数;
大小相同;
例如一块 6x5 的巧克力可以切出 6 块 2x2 的巧克力或者 2 块 3x3 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么?
输入描述
第一行包含两个整数 ,N,K (1≤N,K≤1e5)。
以下 N 行每行包含两个整数Hi,Wi (1≤Hi,Wi≤1e5)。
输入保证每位小朋友至少能获得一块 1x1 的巧克力。
输出描述
输出切出的正方形巧克力最大可能的边长。
输入输出样例
示例
输入
2 10 6 5 5 6输出
2
白话讲解:
有k个小朋友来家里,而我有N块巧克力,如何切出k个正方形,且每个正方形面积最大,输出边长
题解:
边越大则面积越大,但能分的块数就越少,所以我们要找到的是一个边最大,且块数等于k的边长
这题与上题的区别为,正方形的边长a不满足 a满足题意 比a大的都满足题意.但比a小的都满足题意,所以这题的区间为右半边为开区间,也即left=mid,right=mid-1.
check函数为wi/e*hi/e 这里可以理解为,巧克力总面积除以每一块巧克力的面积,即为块数,为什么是除/边长呢?向下取整.之后若>=k则说明满足题意返回即可,当所有巧克力切完还不满足,则返回false
代码实现:
#include <iostream>
using namespace std;
const int N=10010;
int h[N],w[N];
int n=0,k=0;
bool check(int e)
{int res=0;for(int i=0;i<n;i++){res+=(h[i]/e)*(w[i]/e);if(res>=k)return true;}return false;
}
int main()
{cin>>n>>k;for(int i=0;i<n;i++){cin>>h[i]>>w[i];}int l=1,r=1e5;while(l<r){int mid=l+r+1>>1;if(check(mid))l=mid;else r=mid-1;}printf("%d",l);return 0;
}完结撒花:
🌈本篇博客的内容【分巧克力、机器人跳跃、数的范围】已经结束。
🌈若对你有些许帮助,可以点赞、关注、评论支持下博主,你的支持将是我前进路上最大的动力。
🌈若以上内容有任何问题,欢迎在评论区指出。若对以上内容有任何不解,都可私信评论询问。
🌈诸君,山顶见!
相关文章:

【二分查找】分巧克力、机器人跳跃、数的范围
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

Hyperf使用RabbitMQ消息队列
Hyperf连接使用RabbitMQ消息中间件 传送门 使用Docker部署RabbitMQ,->传送门<使用Docker部署Hyperf,->传送门-< 部署环境 安装amqp扩展 composer require hyperf/amqp安装command命令行扩展 composer require hyperf/command配置参数 假…...
【Linux】P3 用户与用户组
用户与用户组root 超级管理员设置超级管理员密码切换到超级管理员sudo 临时使用超级权限用户与用户组用户组管理用户管理getentroot 超级管理员 设置超级管理员密码 登陆后不会自动开启 root 访问权限,需要首先执行如下步骤设定 root 超级管理员密码 1、解除 roo…...

Spring核心模块——Aware接口
Aware接口前言基本内容例子结尾前言 Spring的依赖注入最大亮点是所有的Bean对Spring容器对存在都是没有意识到,Spring容器中的Bean的耦合度是很低的,我们可以将Spring容器很容易换成其他的容器。 但是实际开发的时候,我们经常要用到Spring容…...

Linux网络编程 第六天
目录 学习目标 libevent介绍 libevent的安装 libevent库的使用 libevent的使用 libevent的地基-event_base 等待事件产生-循环等待event_loop 使用libevent库的步骤: 事件驱动-event 编写一个基于event实现的tcp服务器: 自带buffer的事件-buff…...
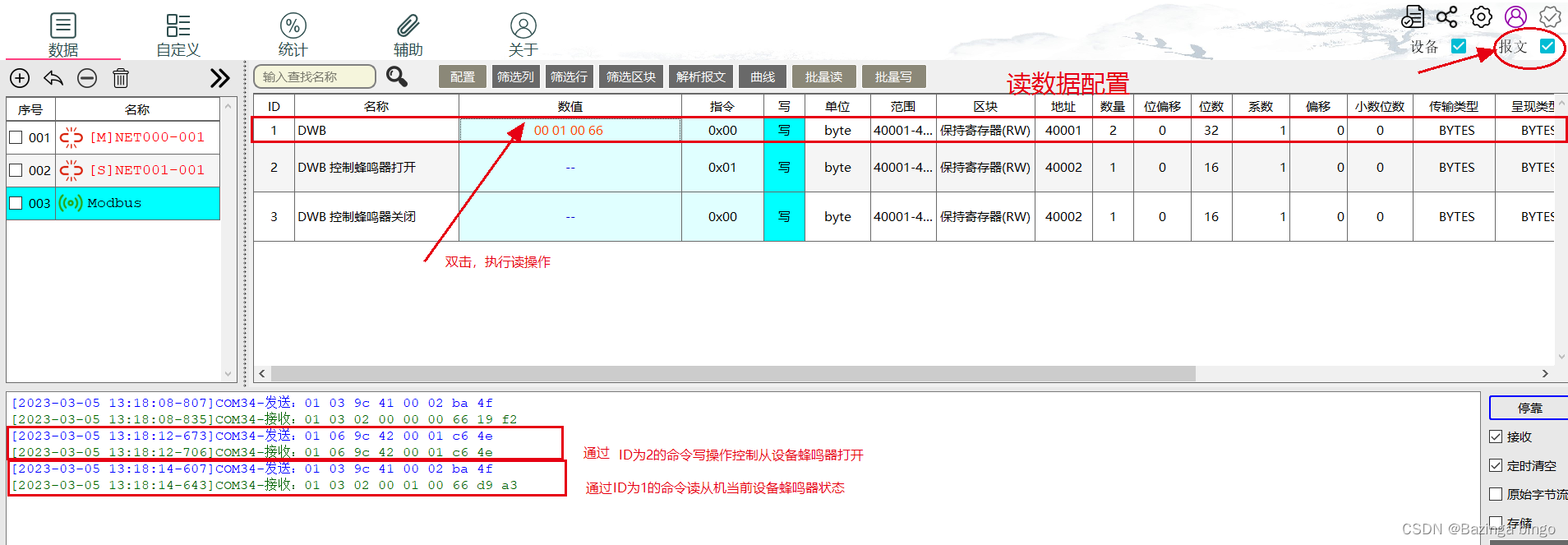
STM32开发(六)STM32F103 通信 —— RS485 Modbus通信编程详解
文章目录一、基础知识点二、开发环境三、STM32CubeMX相关配置1、STM32CubeMX基本配置2、STM32CubeMX RS485 相关配置四、Vscode代码讲解五、结果演示以及报文解析一、基础知识点 了解 RS485 Modbus协议技术 。本实验是基于STM32F103开发 实现 通过RS-485实现modbus协议。 准备…...

AcWing1049.大盗阿福题解
前言如果想看状态机的详解,点机这里:dp模型——状态机模型C详解1049. 大盗阿福阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有 N家店铺,每家店中都有一些现金。阿福事先调查得知,只有当…...

python日志模块,loggin模块
python日志模块,loggin模块loggin模块日志的格式处理器种类日志格式的参数使用loggin模块 logging库采用模块化方法,并提供了几类组件:记录器,处理程序,过滤器和格式化程序。 记录器(Logger)&a…...
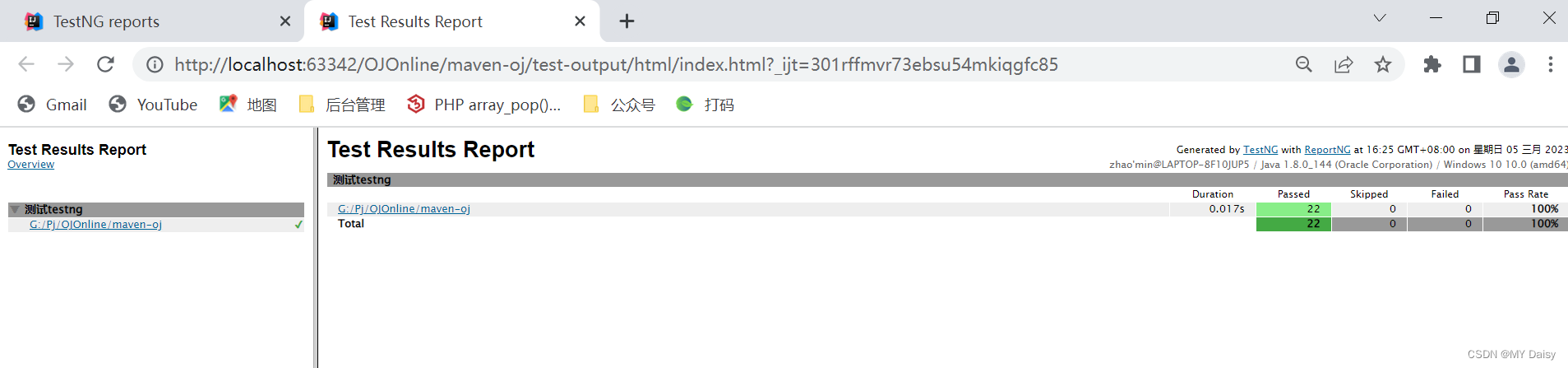
接口自动化入门-TestNg
目录1.TestNg介绍2、TestNG安装3、TestNG使用3.1 编写测试用例脚本3.2 创建TestNG.xml文件(1)创建testng.xml文件(2)修改testng.xml4、测试报告生成1.TestNg介绍 TestNg是Java中开源的自动化测试框架,灵感来源于Junit…...

Spring AOP —— 详解、实现原理、简单demo
目录 一、Spring AOP 是什么? 二、学习AOP 有什么作用? 三、AOP 的组成 3.1、切面(Aspect) 3.2、切点(Pointcut) 3.3、通知(Advice) 3.4、连接点 四、实现 Spring AOP 一个简…...

(蓝桥真题)异或数列(博弈)
题目链接:P8743 [蓝桥杯 2021 省 A] 异或数列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 样例输入: 4 1 1 1 0 2 2 1 7 992438 1006399 781139 985280 4729 872779 563580 样例输出: 1 0 1 1 分析:容易想到对于异或最大值…...

4万字数字政府建设总体规划方案WORD
本资料来源公开网络,仅供个人学习,请勿商用。部分资料内容: 我省“数字政府”架构 (一) 总体架构。 “数字政府”总体架构包括管理架构、业务架构、技术架构。其中,管理架构体现“管运分离”的建设运营模式…...

CCF/CSP 201709-2公共钥匙盒100分
试题编号:201709-2试题名称:公共钥匙盒时间限制:1.0s内存限制:256.0MB问题描述:问题描述 有一个学校的老师共用N个教室,按照规定,所有的钥匙都必须放在公共钥匙盒里,老师不能带钥…...

【OC】Blocks模式
1. Block语法 Block语法完整形式如下: ^void (int event) {printf("buttonId:%d event%d\n", i, event); }完整形式的Block语法与一般的C语言函数定义相比,仅有两点不同。 没有函数名。带有“^”(插入记号)。 因为O…...
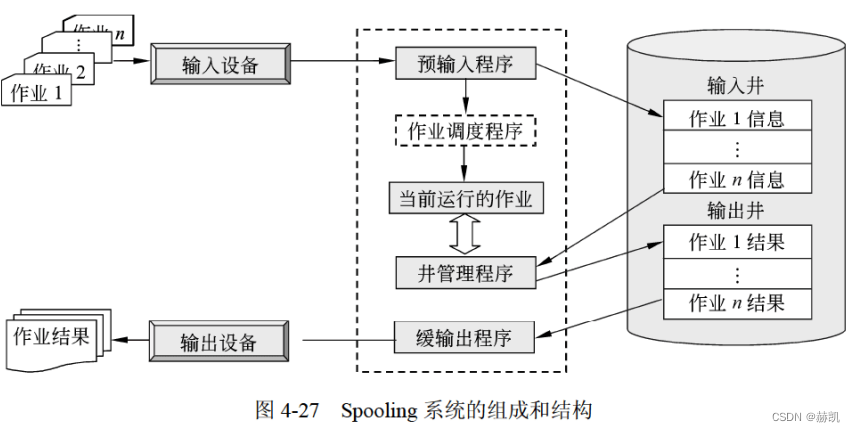
软件设计师教程(七)计算机系统知识-操作系统知识
软件设计师教程 软件设计师教程(一)计算机系统知识-计算机系统基础知识 软件设计师教程(二)计算机系统知识-计算机体系结构 软件设计师教程(三)计算机系统知识-计算机体系结构 软件设计师教程(…...

蓝桥杯2023/3/2
1. 小蓝正在学习一门神奇的语言,这门语言中的单词都是由小写英文字母组 成,有些单词很长,远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词,他准备不再完全记忆这些单词,而是根据单词中哪个字母出现得最…...

【IoT】创业成功不可或缺的两个因素:能力和趋势
今天就来谈谈能力和趋势究竟哪个更重要的问题。 在谈成功的十大要素时,我曾经讲到: 一命、二运、三风水,这三个要素几乎不涉及任何个人的努力。 而趋势跟这三个要素又是息息相关的,这也类似雷军所说的飞猪理论。 只要风足够大&…...

2020蓝桥杯真题日期格式 C语言/C++
问题描述 小蓝要处理非常多的数据, 其中有一些数据是日期。 在小蓝处理的日期中有两种常用的形式: 英文形式和数字形式。 英文形式采用每个月的英文的前三个宁母作为月份标识, 后面跟两位数字 表示日期, 月份标识第一个字母大写, 后两个字母小写, 日期小于 10 时要补 前导 0s…...
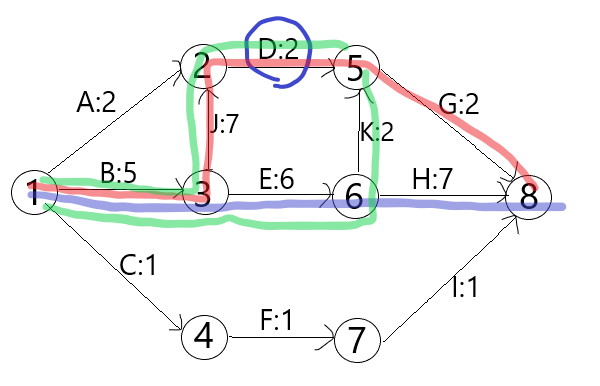
总时差与自由时差
定义总时差(总浮动时间)(TF,Total Free Time,不耽误项目总进度)LS(Latest Start)-ES(Earliest Start)LF(Latest Finish)-EF࿰…...

LeetCode两个数组的交集-跳跃游戏- 最长有效括号
两个数组的交集 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 示例 1: 输入:nums1 [1,2,2,1], nums2 [2,2] 输出:[2] 示例 2: 输入&…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
