你是谁,便会遇见谁
就会进什么样的圈子。努力提升自己,才是提升阶层最可靠的方法。
在人生的舞台上,每一个人都是自己人生的主角。而在这个旅程中,我们会遇见各种各样的人,进入不同的社交圈子。正如一句古训所说:“你是谁,便会遇见谁,就会进什么样的圈子。”这句话揭示了人际关系的深层次法则,也提醒我们在这个纷繁复杂的社会中如何更好地定位自己。
首先,了解自己是建立良好人际关系的关键。每个人都有独特的性格、价值观和兴趣爱好。当我们真正了解自己,知道自己是谁,想要追求什么样的生活目标时,我们就能更好地选择适合自己的人际圈。对自己的认知不仅是对内心的深刻剖析,也是对外在世界更清晰的认识。只有清晰认识自己,我们才能更好地与他人沟通,建立真实而稳固的人际关系。
其次,人际关系的质量直接关系到我们所处的社交圈。选择和积极向上的人为伍,可以让我们收获更多的正能量,激发自己的潜力。在这个过程中,我们应当努力提升自己,不断学习成长。正如谚语所说:“努力提升自己,才是提升阶层最可靠的方法。”只有不断努力学习、提升自己的综合素质,我们才能更好地适应不同的社交场合,与更广泛的人群建立联系。
最后,要打破人际圈的局限,我们需要保持开放心态,勇敢尝试与不同背景、不同经历的人交往。在拓宽人际圈的过程中,我们可能会遇到各种挑战,但正是这些挑战让我们更加坚强,更具包容力。同时,通过与多元化的人群互动,我们也能够获得更广泛的知识和经验,从而更好地理解这个多彩的世界。
总的来说,人际关系是人生中不可或缺的一部分。了解自己,选择积极向上的人际圈,努力提升自己,保持开放心态,这些都是打破人际圈的关键。通过这样的努力,我们可以更好地融入社会,拥有更多的机会和资源,实现自己的人生目标。因此,让我们勇敢地迎接各种人际挑战,成就更丰富多彩的人生。
相关文章:

你是谁,便会遇见谁
就会进什么样的圈子。努力提升自己,才是提升阶层最可靠的方法。 在人生的舞台上,每一个人都是自己人生的主角。而在这个旅程中,我们会遇见各种各样的人,进入不同的社交圈子。正如一句古训所说:“你是谁,便…...
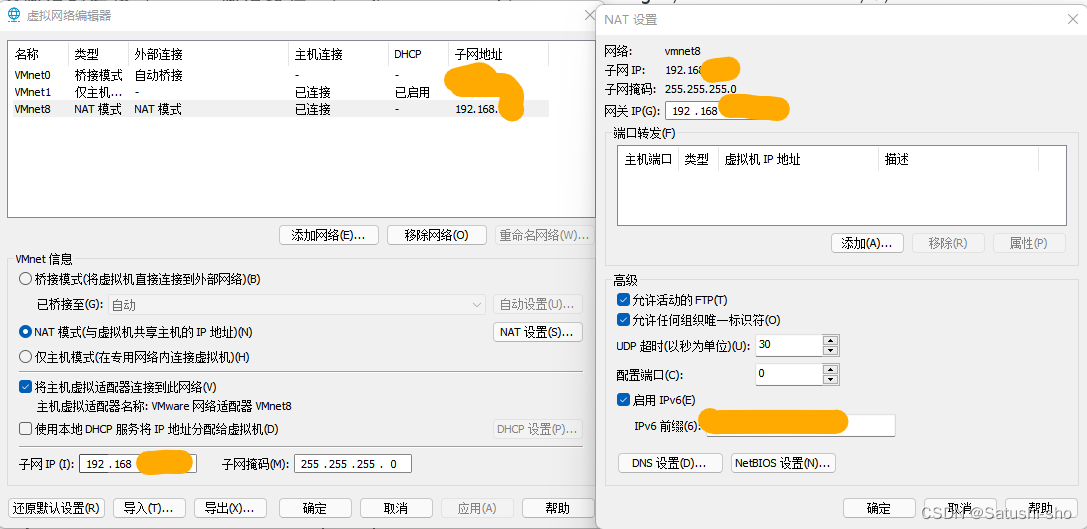
Linux/Centos 部署静态IP,解决无法访问目标主机、Destination Host Unreachable、无法ping通互联网的问题
Linux/Centos 部署IP,解决无法访问目标主机、Destination Host Unreachable、无法ping通互联网的问题 Linux/Centos 部署静态IP查物理机/自身电脑的IP设置VMware上的虚拟网络编辑器设置网卡IP,激活至此就可访问百度了 Linux/Centos 部署静态IP 需要注意…...
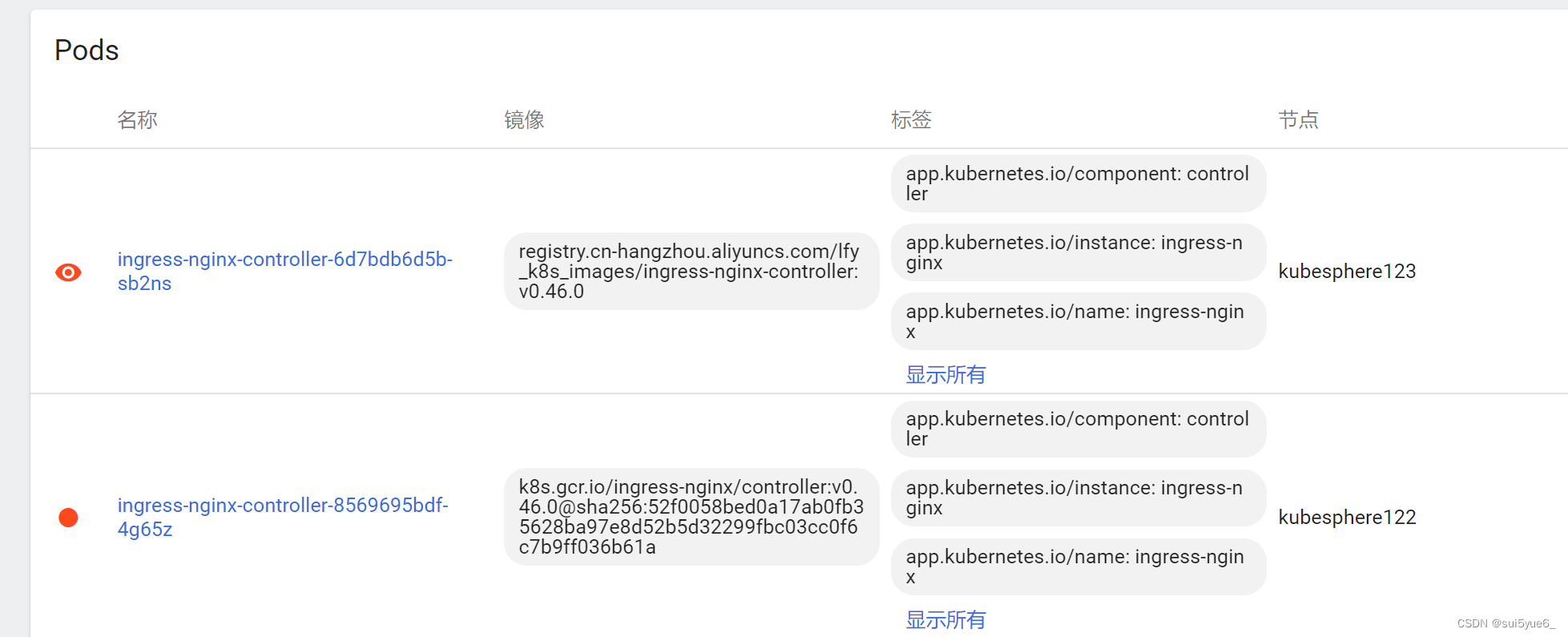
在学习云原生的时候,一直会报错ImagePullBackOff Back-off pulling image
在学习云原生的时候,一直会报错 (见最后几张图) ImagePullBackOff Back-off pulling image 然后我就在像。这个配置的镜像是不是可以自己直接下载,但是好像不怎么搜索得到 然后就在想,这个lfy_k8s_images到底是个啥玩…...

Android Activity跳转详解
在Android应用程序中,Activity之间的跳转是非常常见的操作,通过跳转可以实现不同界面之间的切换和交互。在本篇博客中,我们将介绍Android中Activity跳转的相关知识,包括基本跳转、传递参数、返回数据以及跳转到浏览器、拨号应用和…...

计算机网络(2)-----数据链路层
目录 一.数据链路层的基本概念 二.数据链路层的功能概述 功能一:为网络层提供服务。无确认无连接服务,有确认无连接服务,有确认面向连接服务。 功能二:链路管理,即连接的建立、维持、释放(用于面向连接的服务)。 功能三:组帧 透明传输:…...

贪心算法(算法竞赛、蓝桥杯)--修理牛棚
1、B站视频链接:A27 贪心算法 P1209 [USACO1.3] 修理牛棚_哔哩哔哩_bilibili 题目链接:[USACO1.3] 修理牛棚 Barn Repair - 洛谷 #include <bits/stdc.h> using namespace std; const int N205; int m,s,c,ans; int a[N];//牛的位置标号 int d[N…...

【AIGC】微笑的秘密花园:红玫瑰与少女的美好相遇
在这个迷人的画面中,我们目睹了一个迷人的时刻,女子则拥有一头柔顺亮丽的秀发,明亮的眼睛如同星河般璀璨,优雅而灵动,她的微笑如春日暖阳,温暖而又迷人。站在红玫瑰花瓣的惊人洪水中。 在一片湛蓝无云的晴…...

vue3 中 主题定制
vue3 中 主题定制 背景 做多主题定制,黑/白 ,里面还要再分各种颜色,每次进来都要记住上次的主题设置 效果图 一、目录结构 ├── generated │ ├── theme │ │ └── dark-yellow.ts │ │ └── dark-orange.ts │ │…...
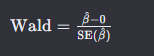
数据分析之Logistic回归分析(二元逻辑回归、多元有序逻辑回归、多元无序逻辑回归)
1、Logistic回归分类 在研究X对于Y的影响时: 如果Y为定量数据,那么使用多元线性回归分析;如果Y为定类数据,那么使用Logistic回归分析。 结合实际情况,可以将Logistic回归分析分为3类: 二元Logistic回归…...

【c++】通讯录管理系统
1.系统功能介绍及展示 2.创建项目 3.菜单实现 4.退出功能实现 5.添加联系人—结构体设计 6.添加联系人—功能实现 7.显示联系人 8.删除练习人—检测联系人是否存在 9.删除联系人—功能实现 10.查找联系人 11.修改联系人 12.清空通讯录 #include <iostream> #include <…...

Tomcat 架构
一、Http工作原理 HTTP协议是浏览器与服务器之间的数据传送协议。作为应用层协议,HTTP是基于TCP/IP协议来传递数据的(HTML文件、图片、查询结果等),HTTP协议不涉及数据包(Packet)传输,主要规定了…...

Spring 整合mybatis
目录 1、梳理整合思路 2、整合实现 2.1 环境搭建 2.2 案例 1、梳理整合思路 将MyBatis的DataSource交给Spring IoC容器创建并管理,使用第三方数据库连接池(Druid,C3P0等)代替MyBatis内置的数据库连接池将MyBatis的SqlSessionFactory交给Spring IoC容…...

centos7升级openssl_3
1、查看当前openssl版本 openssl version #一般都是1.几的版本2、下载openssl_3的包 wget --no-check-certificate https://www.openssl.org/source/old/3.0/openssl-3.0.3.tar.gz#解压 tar zxf openssl-3.0.3.tar.gz#进入指定的目录 cd openssl-3.0.33、编译安装遇到问题缺…...

nvidia a100-pcie-40gb环境安装
1.conda create --name torch_li python3.8 2. conda install pytorch1.7.1 torchvision0.8.2 torchaudio0.7.2 cudatoolkit11.0 -c pytorch 环境测试:torch.cuda.is_available() 3.conda remove -n torch_li --all 4.pip install opencv-python-headless 5.pip ins…...

嵌入式 Linux 下的 LVGL 移植
目录 准备创建工程修改配置修改 lv_drv_conf.h修改 lv_conf.h修改 main.c修改 Makefile 编译运行更多内容 LVGL(Light and Versatile Graphics Library)是一个轻量化的、开源的、在嵌入式系统中广泛使用的图形库,它提供了一套丰富的控件和组件…...

js同步和异步请求
2023.3.2今天我学习了同步请求和异步请求的区别: 同步请求: 指代码按照顺序依次执行,每一行代码都要等待上一行代码执行完成后才能继续执行,比如你有两个接口,它会第一个接口请求完才去请求下一个接口。 异步请求&a…...

【Leetcode】2369. 检查数组是否存在有效划分
文章目录 题目思路代码结果 题目 题目链接 给你一个下标从 0 开始的整数数组 nums ,你必须将数组划分为一个或多个 连续 子数组。 如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种 有效 划分: 子数组 恰 由 2 个…...

Laravel Octane 和 Swoole 协程的使用分析
之前在工作中使用 Laravel Octane 的 concurrently 处理并发时,发现在队列和定时任务中不会触发并发效果。经过分析,作了如下猜测:队列和定时任务都属于一个独立的进程,与 Octane 服务无关,而 Octane concurrently 恰恰…...
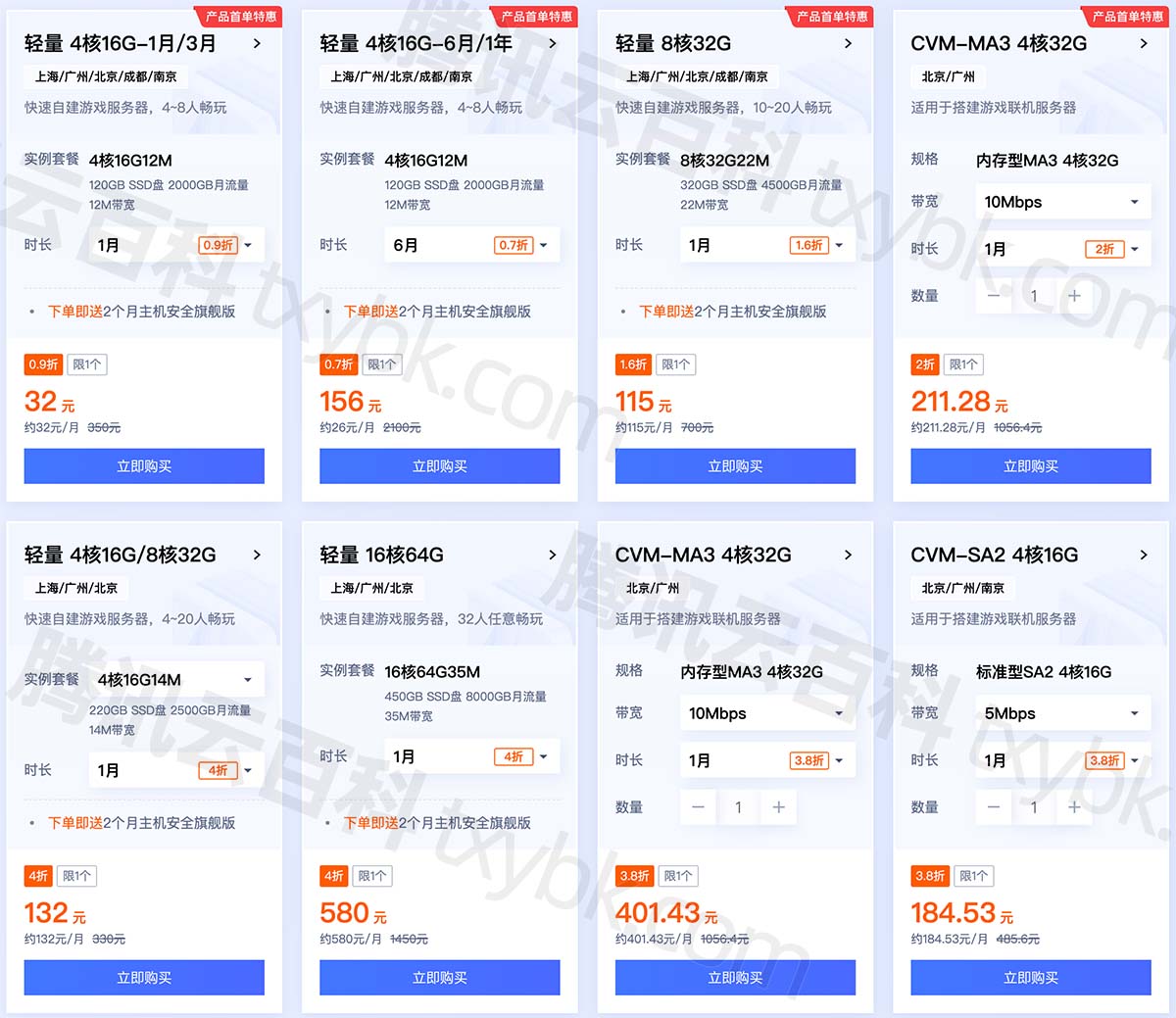
腾讯云又双叕降价,云服务器配置优惠价格表2024新版报价
腾讯云服务器多少钱一年?62元一年起,2核2G3M配置,腾讯云2核4G5M轻量应用服务器218元一年、756元3年,4核16G12M服务器32元1个月、312元一年,8核32G22M服务器115元1个月、345元3个月,腾讯云服务器网txyfwq.co…...

【react native】css踩坑记录
1、IOS上面opacity重叠失效 在 iOS 上,当两个具有相同背景色的元素重叠时,不透明度(opacity)较低的元素会显示在较高的元素上方。 所以考虑使用rgba的形式。 // 对于下面这种写法,如果存在container和activeIndicat…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
