【Unity】机器人末端执行器仿真



机械手臂的末端执行器使用多项式来计算转动角度可能有几个原因:
精确控制:机械臂的运动通常需要高度的精确性,特别是在精密工作或复杂运动轨迹的情况下。多项式,特别是高阶的,可以很好地近似复杂的非线性关系和运动轨迹,从而提供更精细的控制。
模拟物理行为:实际中的物理系统行为通常不是线性的,而是非线性和复杂的。多项式可以模拟这种非线性行为,使得仿真更加接近真实的动力学表现。
传动机械学:在一些情况下,末端执行器的运动取决于多个传动部件的联动效果,这些效果可能涉及到具有非线性特性的机械连杆组、齿轮组或其他传动系统。使用多项式可以帮助建立起行程到角度之间的数学模型,这种转换可能源于实际测量和实验数据的拟合。
补偿误差:多项式可以用于补偿由机械磨损、温度变化或制造公差等因素引起的误差和偏差。通过精确的多项式拟合,能够提升整个系统的精度和可靠性。
便于编程和控制:软件中使用数学公式来描述和控制机械手臂的运动可以简化编程。多项式提供了一种方便的方式来实现这一点,特别是在需要反复求值或者进行实时控制时。
综上所述,使用多项式来计算转动角度可以让末端执行器的运动更加准确、平滑且可预测,使其在执行任务时能到达精确的位置,这对于高精度的机器人应用场景是非常关键的。
在物理系统和机械设计中,这种类型的多项式通常来源于实验数据的回归拟合。设计者们通过测量不同行程值时的实际转动角度,使用数学工具(比如最小二乘法)来找出最佳的系数,以使多项式能最好地符合实验数据点。
理论推导的步骤可能是这样的:
数据采集:通过实验测量末端执行器在一系列已知行程位置时的实际转动角度。
确定多项式阶数:根据数据的复杂程度来决定多项式的阶数。如果系统非常复杂,可能需要一个较高阶的多项式来捕捉所有的非线性特征。
参数拟合:使用数学和统计工具(例如最小二乘法)根据实验数据来拟合多项式参数。
验证模型:将拟合得到的多项式模型的预测与实验数据进行对比,确保其有足够的精确度。
编码实现:将拟合好的多项式嵌入代码中,能够根据输入的行程计算出对应的角度。
在我们的例子中,多项式系数是已经提供在 coefficients 数组中的固定值。理论推导在现实中可能包括详尽的实验和数据分析过程,但在这里由于我们没有实际的硬件和实验数据,我们仅能依赖于代码中提供的信息来理解这个关系是如何被封装在多项式函数中的。
多项式回归在机器人末端执行器中的应用原理是利用多项式函数来拟合机器人末端的位置和姿态误差,从而实现对末端执行器的精度补偿。具体来说,有以下几个步骤:
首先,利用激光跟踪仪或其他外部测量设备,采集机器人末端执行器的实际位置和姿态数据,以及对应的关节位形数据,作为训练样本。
然后,利用多项式回归方法,建立机器人末端的位置和姿态误差与关节位形之间的映射关系,得到误差模型的多项式系数。
最后,当机器人末端执行器需要执行精密操作时,根据当前的关节位形,利用误差模型预测末端的位置和姿态误差,并对末端执行器进行相应的补偿,从而提高运动精度。
多项式回归在机器人末端执行器中的应用原理的优点是可以处理非线性的误差关系,且计算简单,易于实现。缺点是需要大量的训练样本,且对多项式次数的选择敏感,过高或过低的次数都会影响拟合效果。
如果你想了解更多关于多项式回归在机器人末端执行器中的应用原理的相关内容,你可以参考以下的资源:
基于模型和数据驱动的机器人6D位姿估计方法:这篇文章介绍了一种结合多项式回归和测量平差的方法,实现机器人末端的高精度位姿估计。
实现多工位协同:机器人末端精度补偿装置在工业自动化中的应用探索与成功案例分享:这篇文章分享了一种基于传感器的机器人末端精度补偿装置的设计和应用,以及在不同场景下的成功案例。
机器人运动学分析与动力学分析主要作用:这篇文章概述了机器人运动学和动力学的基本概念和作用,以及在机器人控制中的应用。
机器人末端执行器设计与控制研究:这篇文章综述了机器人末端执行器的分类、设计原理和控制方法,以及在不同领域的应用前景。
源: 与必应的对话, 2024/3/1
(1) 基于模型和数据驱动的机器人6D位姿估计方法. http://jst.tsinghuajournals.com/article/2022/4307/20220302.htm.
(2) 实现多工位协同:机器人末端精度补偿装置在工业自动化中的应用探索与成功案例分享 - 知乎. https://zhuanlan.zhihu.com/p/648396549.
(3) 机器人运动学分析与动力学分析主要作用-CSDN博客. https://blog.csdn.net/m0_61712829/article/details/135184597.
(4) 机器人末端执行器设计与控制研究 - 百度文库. https://wenku.baidu.com/view/8f3e9ed4f624ccbff121dd36a32d7375a417c6c8.html.
(5) 机器学习理论(六)多项式回归 - 知乎 - 知乎专栏. https://zhuanlan.zhihu.com/p/77555547.
多项式拟合回归是一种使用多项式函数来拟合数据的回归方法。它可以处理非线性关系,但本质上仍然是线性回归,因为它是关于多项式系数的线性方程。多项式拟合回归的难点在于如何选择合适的多项式次数,以及如何避免过拟合或欠拟合的问题。¹²
如果你想了解更多关于多项式拟合回归的理论和实践,你可以参考以下的资源:
机器学习(1)--线性回归和多项式拟合:这篇文章介绍了线性回归和多项式拟合的基本原理和数学推导,以及用Matlab和Python实现的代码示例。
多项式回归(Polynomial Curve Fitting):这篇文章用图形和代码展示了不同多项式次数对拟合效果的影响,以及如何用正则化来防止过拟合。
多项式回归详解 从零开始 从理论到实践:这篇文章从零开始用Python实现了多项式回归的算法,包括数据生成、损失函数、梯度下降、正则化等步骤。
多项式回归_百度百科:这篇文章给出了多项式回归的定义、分类、特点、优缺点等概述。
十分钟掌握多项式回归:拟合非线性关系:这篇文章用简洁的语言和图示解释了多项式回归的原理和应用,以及如何用sklearn库进行多项式回归的操作。
源: 与必应的对话, 2024/3/1
(1) 机器学习(1)--线性回归和多项式拟合 - 知乎 - 知乎专栏. https://zhuanlan.zhihu.com/p/80969579.
(2) 多项式回归(Polynomial Curve Fitting) - 知乎 - 知乎专栏. https://zhuanlan.zhihu.com/p/113622703.
(3) 机器学习(1)--线性回归和多项式拟合 - 知乎 - 知乎专栏. https://zhuanlan.zhihu.com/p/80969579.
(4) 多项式回归(Polynomial Curve Fitting) - 知乎 - 知乎专栏. https://zhuanlan.zhihu.com/p/113622703.
(5) 多项式回归详解 从零开始 从理论到实践-CSDN博客. https://bing.com/search?q=多项式拟合回归.
(6) 多项式回归详解 从零开始 从理论到实践-CSDN博客. https://blog.csdn.net/weixin_44225602/article/details/112752565.
(7) 多项式回归_百度百科. https://baike.baidu.com/item/多项式回归/21505384.
(8) 十分钟掌握多项式回归:拟合非线性关系 - 知乎. https://zhuanlan.zhihu.com/p/53977691.
相关文章:

【Unity】机器人末端执行器仿真
机械手臂的末端执行器使用多项式来计算转动角度可能有几个原因: 精确控制:机械臂的运动通常需要高度的精确性,特别是在精密工作或复杂运动轨迹的情况下。多项式,特别是高阶的,可以很好地近似复杂的非线性关系和运动轨迹…...
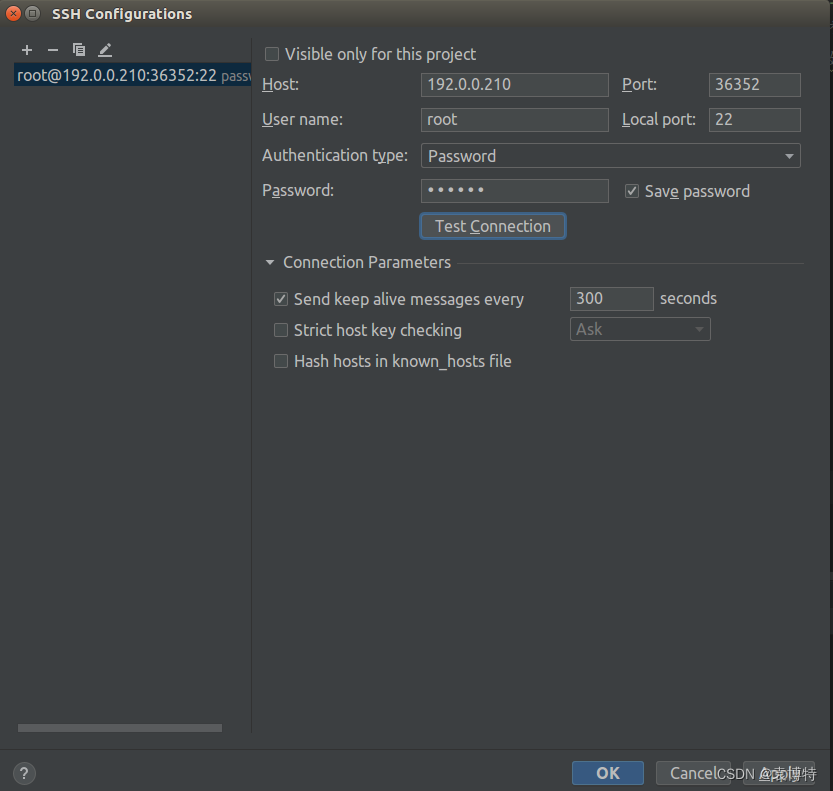
更换个人开发环境后,pycharm连接服务器报错Authentication failed
原因:服务器中更换个人开发环境后,密码变了。 解决:在pycharm中修改服务器开发环境密码即可。 1 找到Tools-Depolyment-Configuration 2 点击SSH Configuration后的省略号 3 修改这里面的Password即可...
E - Bad Juice
解题思路 由于最后返回一个01字符串表示所选人的状态要求人数最少,即字符串长度最少而要用最少的字符,找出则返回的字符为二进制下的编号这样利用了所有的01字符号人表示二进制下位的情况注意对于2的次方项,只需要有位,可以用位均…...
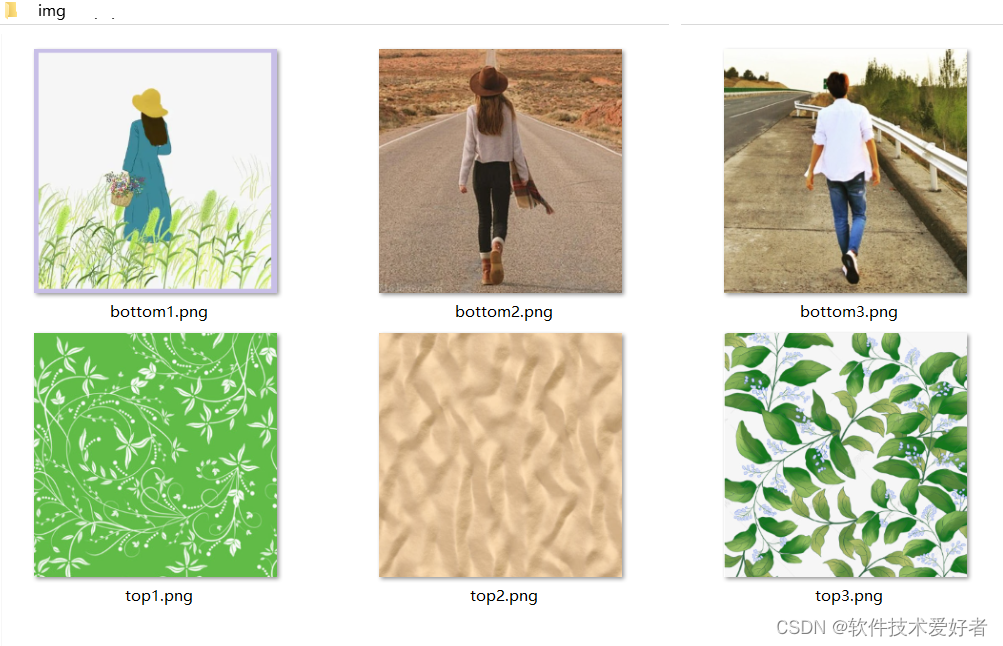
用HTML5的<canvas>元素实现刮刮乐游戏
用HTML5的<canvas>元素实现刮刮乐游戏 用HTML5的<canvas>元素实现刮刮乐,要求:将上面的“图层”的图像可用鼠标刮去,露出下面的“图层”的图像。 示例从简单到复杂。 简单示例 准备两张图像,我这…...

TypeScript + react 中 TypeScript 的加入后 , 有哪些优化项目
在使用 TypeScript 结合 React 进行开发时,TypeScript 提供了许多优化和增强代码质量的方式。以下是一些关键的优化操作和最佳实践: 强类型组件属性(Props)和状态(State): 使用接口或类型别名定义组件的 pr…...
)
Redis学习路径(构建体系)
学习路径 掌握数据类型(分析底层数据结构)和缓存的基本使用 (理论使用) 掌握 redis 实现高性能,高可靠、高可用技术 (理论)学习redis源代码底层实现 (底层实现) 先来一个引言,比较宏观的角度…...

【README 小技巧】 展示gitee中开源项目start
【README 小技巧】 展示gitee中开源项目start <a target"_blank" hrefhttps://gitee.com/wujiawei1207537021/wu-framework-parent><img srchttps://gitee.com/wujiawei1207537021/wu-framework-parent/badge/star.svg altGitee star/></a>...

tcping实用小工具
Tcping实用小工具命令详解 一、tcping介绍 tcping:tcping命令基于tcp协议监控,可以从较低级别的协议获得简单的,可能不可靠的数据报服务。 原则上,TCP应该能够在从容硬线连接到分组交换或电路交换网络的各种通信系统之上操作。 …...

【Web】Java反序列化之CC2——commons-collections4的新链之一
目录 关于commons-collections4 一个重要的思维模型 触发Transform的关键类:TransformingComparator 反序列化的入口:PriorityQueue Exp 关于commons-collections4 commons-collections4 是 Apache Commons 组件库中的一个项目,它是对旧…...
golang使用gorm操作mysql1
1.mysql连接配置 package daoimport ("fmt""gorm.io/driver/mysql""gorm.io/gorm""gorm.io/gorm/logger" )var DB *gorm.DB// 连接数据库,启动服务的时候,init方法就会执行 func init() {username : "roo…...

Flutter异常上报及性能监控实现
1. 页面异常监测 在Flutter中,通常用FlutterError监测Flutter框架抛出的异常,用runZonedGuarded监测应用中用户代码异常。 class AppGuarded {run(Widget app) {//1. 用FlutterError监测flutter框架抛出的异常FlutterError.onError (FlutterErrorDetail…...
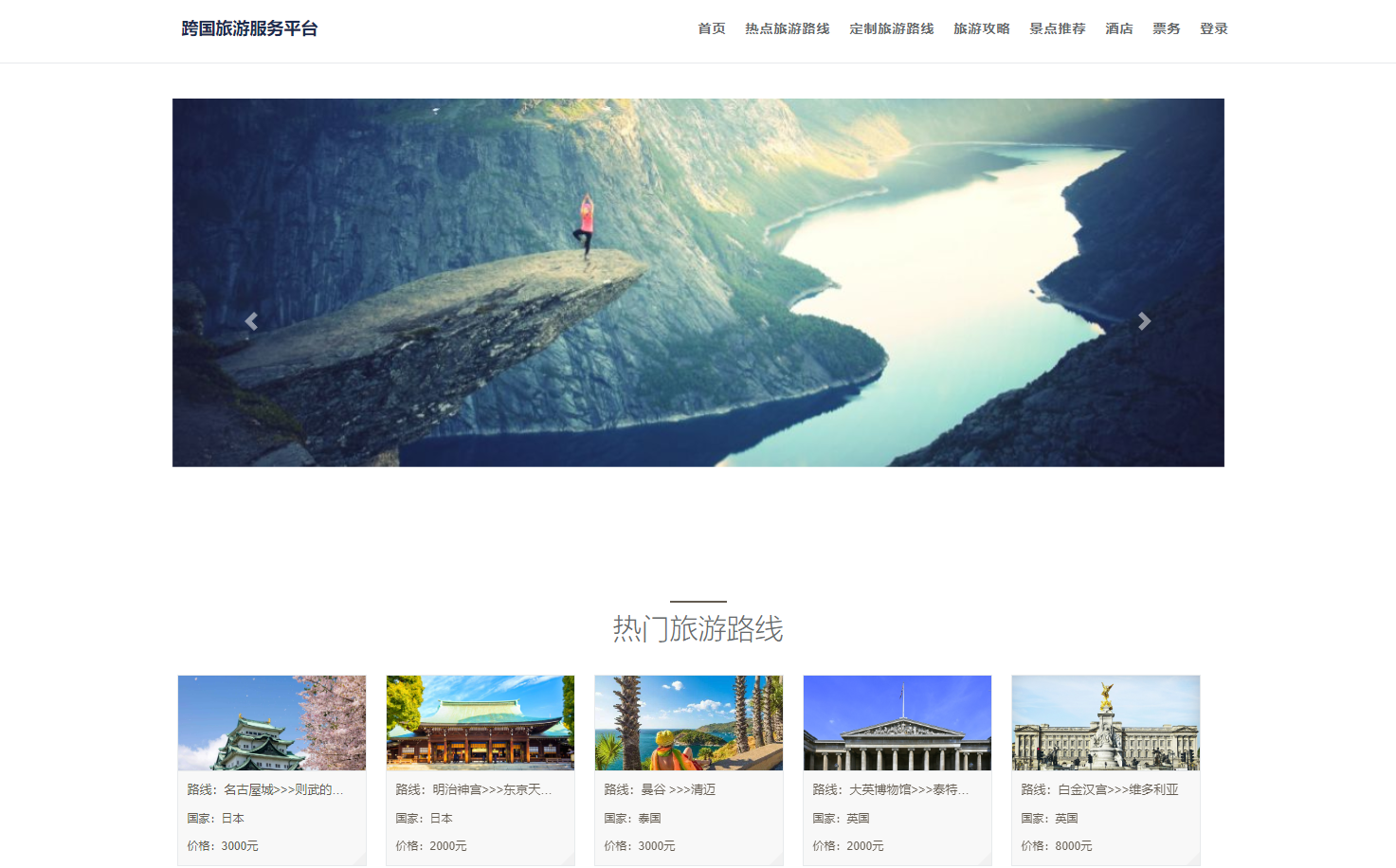
基于springboot+vue的工厂车间管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

Java基础 - Stream 流:Stream API的终端操作
在前两篇博客中,我介绍了构建 Stream 流的多种方式,以及 Stream API 的中间操作,如果你还没有阅读,你可以点击这里和这里查看。 Java基础 - Stream 流:构建流的多种方式 Java基础 - Stream 流:Stream API…...
)
高级语言期末2009级A卷(计算机学院)
1.编写函数,打印下列序列0,1,1,2,3,5,8,13,21,34...(斐波那契序列)的前n项 #include <stdio.h>int main() {int x0,y1,z,n;scanf("%d",&…...

docker-compose搭建php开发环境
Docker Compose简介 Compose 是用于定义和运行多容器 Docker 应用程序的工具。通过 Compose,您可以使用 YML 文件来配置应用程序需要的所有服务。然后使用一个命令,就可以从 YML 文件配置中创建并启动所有服务。而DockerCompose作为一种容器编排工具&…...
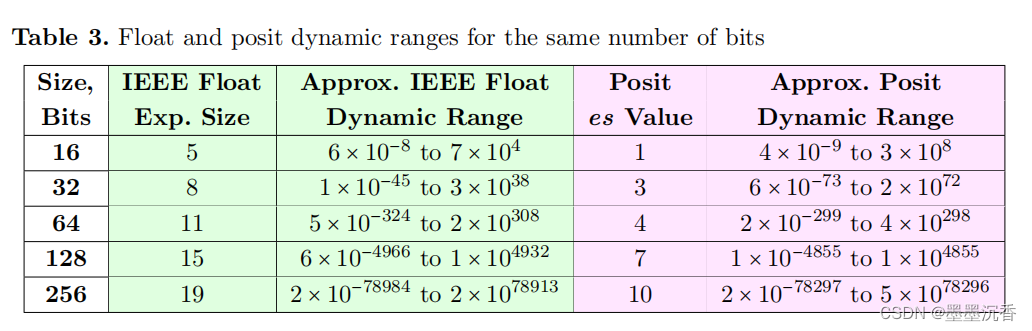
翻译论文:Beating Floating Point at its Own Game: Posit Arithmetic(一)
仅作记录学习使用,侵删 原文Beating Floating Point at its Own Game: Posit Arithmetic 参考翻译Posit: 替换IEE754的新方式 | SIGARCH 摘要 IEEE标准754浮点数(浮点数)的直接接点替换 Posit的优势 不需要区间算术或可变大小操作数 如…...

【数据结构-图论】并查集
并查集(Union-Find)是一种数据结构,它提供了处理一些不交集的合并及查询问题的高效方法。并查集主要支持两种操作: 查找(Find):确定某个元素属于哪个子集,这通常意味着找到该子集的…...

云计算时代的运维: 职业发展方向与岗位选择
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua,在这里我会分享我的知识和经验。&#x…...

java锁底层概述
Java中的锁是并发编程中核心的同步机制之一,用于控制多个线程对共享资源的访问,以保证数据的一致性和完整性。Java锁的底层实现依赖于操作系统的原生线程模型和Java虚拟机(JVM)的实现。这里主要讨论两种常见的锁:synch…...

win10如何添加指纹登陆
1、首先进入设置,进入下一个设置页面 2、在下一个设置页面内,我们直接使用右上角的搜索框,输入“指纹/finger”进行搜索。回车之后进入设置指纹登陆选项 3、设置指纹登陆的前期是设置好你的密码和pin码(先要设定登录密码和pin码),这里pin和密码都可以直接登陆我们的win10,设…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
