Stwo:基于Circle STARK和M31的下一代STARK证明系统
1. 引言
StarkWare团队和Polygon Labs团队,历时数月,构造了基于Mersenne素数域M31的Circle STARK协议,通过使用M31 over a circle,可基于任意有限域构造高效STARKs,具体见2024年2月19日论文《Circle STARKs》。
基于Circle STARK协议,StarkWare团队开发了超快的证明系统:Stwo,大幅改进了现有Stone prover(见Stone Prover:StarkWare的STARK Prover)。
Stwo开源代码见:
- https://github.com/starkware-libs/stwo(Rust)
BabyBear域背景知识见:
- RISC Zero的Babybear域 及其 扩域
- 技术探秘:在RISC Zero中验证FHE——RISC Zero应用的DevOps(2)
Mersenne素数域M31背景知识见:
- Plonky3 Mersenne素数域的Reed-Solomon codes设计
- 基于circle group的Reed-Solomon codes
传统STARKs协议,其组成步骤要求代数结构:
- 需要一个素数域 p p p,其 p − 1 p-1 p−1可被2的大幂整除。
即传统STARKs,其所使用的域内要有一个smooth order的cyclic group。
原因在于STARKs协议中有2大核心:
- FFT:使用FFT算法来高效插值点,并编写包含相邻行的约束。
- FRI
这就排除了许多尺寸较小的域,尽管这些域非常适合高效计算。如,Mersenne素数域M31,其 p = 2 31 − 1 p=2^{31}-1 p=231−1,而 p − 1 = 2 ( 2 30 − 1 ) p-1=2(2^{30}-1) p−1=2(230−1)甚至不能被 4 4 4整除。从而陷入僵局:
- 传统STARKs协议无法与M31结合使用
数年前,曾希望让STARKs协议适用于2种主流加密曲线:secp256k1 和 secp256r1。但这2条曲线也不满足上面的要求。为此,还研究出了Elliptic Curve Fast Fourier Transform (ECFFT) Part I: Fast Polynomial Algorithms over all Finite Fields论文,其使用椭圆曲线为FFT和FRI提供了替代的结构源,在该论文中,详细介绍了将STARKs用于任意域的机制——使用某椭圆曲线的cyclic group。
为能让M31与STARKs结合使用,StarkWare团队和Polygon Labs团队合作,最终有了Circle STARKs:
- 一种紧凑、优雅的协议,避免了ECFFT论文的重型机制。
- 简而言之:当 p + 1 p+1 p+1可被2的大幂整除时(如M31),基于该素数域的circle curve( x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1)提供了适于FFT和FRI所需的结构。

2. Stwo:基于Circle STARK和M31的下一代STARK证明系统
Stwo:
- 利用 Circle STARK 和各种其他优化来带来前所未有的证明性能。
Stone(为St-one)为一代,而Stwo(S-two)为二代。已基于Stone系统构建的应用链和Starknet,都不受影响,高级Cairo将与Stwo完全兼容。当时机到来时,Stwo 已准备好推出,Starknet 生态系统(即用户和开发人员)将受益于 Stwo 的下一级别的扩展,而无需执行任何操作!Stwo 将与编写合约的高级Cairo代码兼容,也与Sierra兼容。当前基于Stone的Starknet prover(s),未来将使用Stwo。用户/构建者/dapp 也将在延迟和费用方面受益。
3. 性能对比
在《Circle STARKs》论文中,对基于M31的Circle STARKs,和,基于Babybear域的传统STARK(使用的Babybear代码为https://github.com/Plonky3/Plonky3/commit/86d13ddf269427c4788cdd41f413308a6050f9f3)做了性能对比,要快约1.4倍:

参考资料
[1] StarkWare 2024年3月博客 Stwo Prover: the next-gen of STARK scaling is here
[2] 2024年2月21日 Circle STARKs
相关文章:

Stwo:基于Circle STARK和M31的下一代STARK证明系统
1. 引言 StarkWare团队和Polygon Labs团队,历时数月,构造了基于Mersenne素数域M31的Circle STARK协议,通过使用M31 over a circle,可基于任意有限域构造高效STARKs,具体见2024年2月19日论文《Circle STARKs》。 基于…...
)
笔记本以太网集线器Hub充电可能导致网络异常(貌似是我把服务器网关写错了)
文章目录 笔记本以太网集线器(Hub)充电导致网络异常概述原理分析电源与信号干扰设备热度设备兼容性问题 解决方案升级固件提高设备散热效率选择兼容性好的设备 总结 今天用笔记本以太网直连服务器,一开始能连通,结果以太网hub插上…...

npm ERR! code ETIMEDOUT
在新建vue项目的时候报错 npm ERR! code ETIMEDOUT npm ERR! syscall connect npm ERR! errno ETIMEDOUT npm ERR! network request to https://registry.npmjs.org/vue%2fcli failed, reason: connect ETIMEDOUT 104.16.2.35:443 npm ERR! network This is a problem relate…...
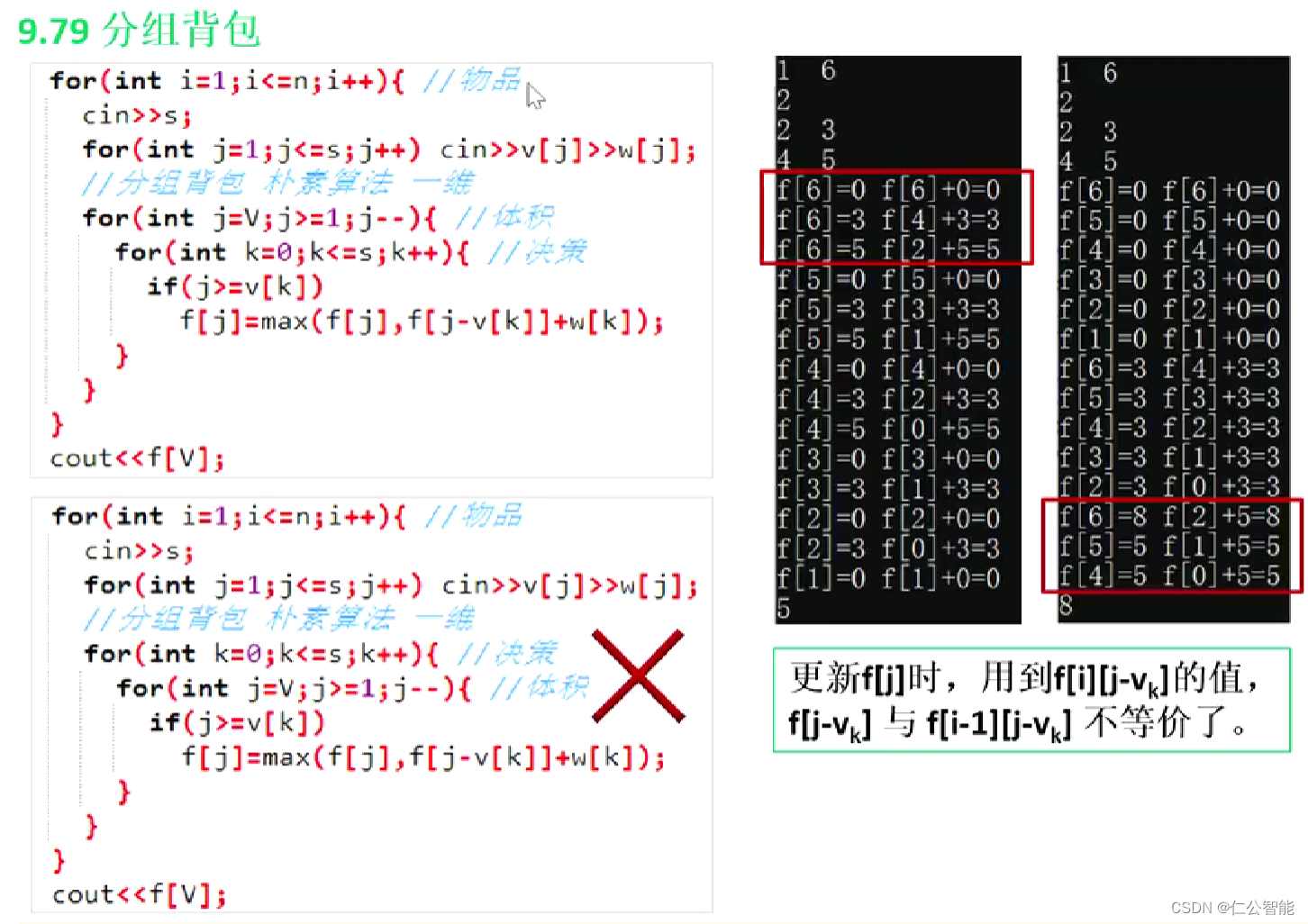
动态规划(算法竞赛、蓝桥杯)--分组背包DP
1、B站视频链接:E16 背包DP 分组背包_哔哩哔哩_bilibili #include <bits/stdc.h> using namespace std; const int N110; int v[N][N],w[N][N],s[N]; // v[i,j]:第i组第j个物品的体积 s[i]:第i组物品的个数 int f[N][N]; // f[i,j]:前i组物品,能放…...

太阳能供电井盖-物联网智能井盖监测系统-旭华智能
在这个日新月异的科技时代,城市的每一个角落都在悄然发生变化。而在这场城市升级的浪潮中,智能井盖以其前瞻性的科技应用和卓越的安全性能,正悄然崭露头角,变身马路上的智能“眼睛”,守护城市安全。 传统的井盖监测系统…...

贪心 Leetcode 455 分发饼干
分发饼干 Leetcode 455 学习记录自代码随想录 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸࿱…...

策略开发:EMA如何计算
EMA的计算原理 EMA 是MA(平滑移动平均线)的另一种形式。全名“加权指数移动平均线”。 2/13就是12日移动平均线的平滑因子,他的意思是指:给予新价格 2/13的权重,给予过去的EMA 11/13的权重。 在计算的时候第一天的M…...

学习Android的第二十天
目录 Android Toast 吐司 常量 常用方法 例子 Android Notification 状态栏通知 Notification 的基本布局 扩展布局 Notification ( 状态栏通知 ) 相关的方法 例子: 参考文档 Android AlertDialog 弹出框 Android Dialog 继承图谱 AlertDialog 几种常…...
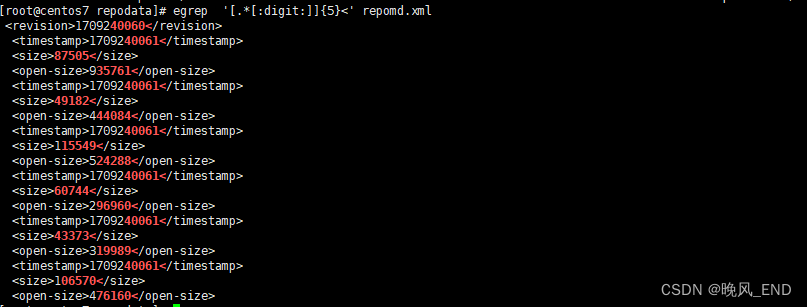
Linux技巧|centos7|重新认识和学习egrep和grep命令
前言: 相信提高文本检索工具,大家脑海里肯定有很多工具会自动跳出来,比如,grep,egrep,sed,cat,more,less,cut,awk,vim,vi…...

css实现背景渐变叠加
线性渐变效果图: .box{width: 100vw;height: 100vh;background:linear-gradient(to bottom,transparent,#fff 30%),linear-gradient(to right,pink,skyblue);}径像渐变效果图: .box{width: 100vw;height: 100vh;background:linear-gradient(to bottom,transparent,#…...
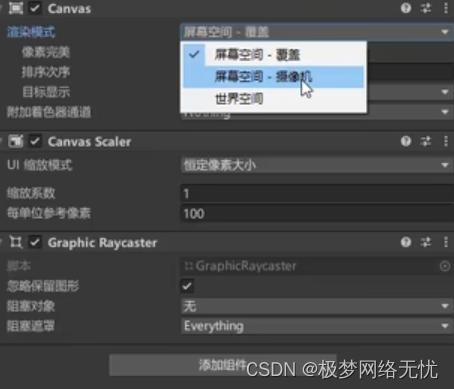
Unity(第二十四部)UI
在游戏开发中,用户界面(UI)是至关重要的一部分。它负责与玩家进行交互,提供信息,并增强游戏的整体体验。Unity 提供了强大的工具和功能来创建和管理 UI。 ui的底层就是画布,创建画布的时候会同时创建一个事…...

VSCode通过SSH连接Docker环境进行开发
文章目录 VSCode 插件Docker 镜像构建镜像部署环境 VSCode 连接本地Docker容器VSCode SSH连接Docker容器VSCode 打开容器内目录文件 VSCode 插件 Remote - SSH Docker 镜像 https://hub.docker.com/_/golang # Golang 镜像 docker pull golang:1.22构建镜像 Dockerfile F…...

【QT】QTableView或QTableWidget 搭配QLineEdit实现数据的搜索显示
在 Qt 中,QTableView 和 QTableWidget 都可以用来实现数据的搜索和显示,但它们的适用场景和实现方式有所不同: QTableView 适用场景:QTableView 适用于更复杂的场景,尤其是当需要处理大量数据或需要高度定制化的表格时…...

Apache Flink连载(三十五):Flink基于Kubernetes部署(5)-Kubernetes 集群搭建-1
🏡 个人主页:IT贫道-CSDN博客 🚩 私聊博主:私聊博主加WX好友,获取更多资料哦~ 🔔 博主个人B栈地址:豹哥教你学编程的个人空间-豹哥教你学编程个人主页-哔哩哔哩视频 目录 编辑...
)
快速幂(c++题解)
题目描述 我们通常把a的b次方记作a^b,为了方便,我们经常直接使用C内置函数pow(a,b)来完成这个工作,但a的b次方就是把a垒乘b次,时间复杂度为O(b),当b值很大时,将会耗去大量时间,所以请同学们不能…...

C#单向链表实现:Append,Move,Delete,InsertAscending, InsertUnAscending,Clear
目录 一、链表定义 二、链表设计 1.先定义一个结点类(Node) 2.再定义链表类(LinkedList)并依次设计其方法 3.再实现删除方法 4.再实现Insert 的方法 5.再增加InsertAscending升序插入 6.再增加 InsertUnAscending 的方法…...

python基础-基本数据类型深入-2.1
目录 元组 什么是元组(tuple) 元组练习-1 元组的基本操作 元组常用内建函数 列表和元组的区别与总结 元组练习-2 元组练习-3 元组 什么是元组(tuple) 与列表(list)一样,元组࿰…...

Android LiveData Cannot add the same observer with different lifecycles
https://www.yxhuang.com/2022/05/29/livedata-add-some-observer-error/ 这篇文章已经解释的很好了。 其实在去年我写的文章, https://blog.csdn.net/jzlhll123/article/details/126593235 中提到了, 其实不论是java或者kotlin,不引用外部的…...

MongoDB聚合运算符:$cmp
文章目录 语法用法举例 $cmp聚合运算符返回连个值的比较结果。 语法 { $cmp: [ <expression1>, <expression2> ] }表达式可以是任何类型,使用标准的BSON比较顺序对不同类型的值进行比较。 用法 $cmp对两个值进行比较,返回: …...

【C++基础知识详细记录】
一、基础知识 C基础知识点的汇总涵盖了许多方面,包括但不限于以下内容: 1. 常量定义 使用#define宏定义常量: #define PI 3.14159265358979323846 // 宏定义一个浮点型常量PI使用const关键字定义常量: const int MAX_SIZE 100;…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
