分类问题经典算法 | 二分类问题 | Logistic回归:公式推导
目录
- 一. Logistic回归的思想
- 1. 分类任务思想
- 2. Logistic回归思想
- 二. Logistic回归算法:线性可分推导
一. Logistic回归的思想
1. 分类任务思想
分类问题通常可以分为二分类,多分类任务;而对于不同的分类任务,训练的主要目标是不变的,即找到一个分类器,这个分类器可以对新输入的数据进行判断,以确定该数据是属于哪个类别
对于分类任务,我们常设函数为 A x 1 + B x 2 + C = 0 Ax_{1}+Bx_{2}+C = 0 Ax1+Bx2+C=0
下面我们先来讨论二分类任务:
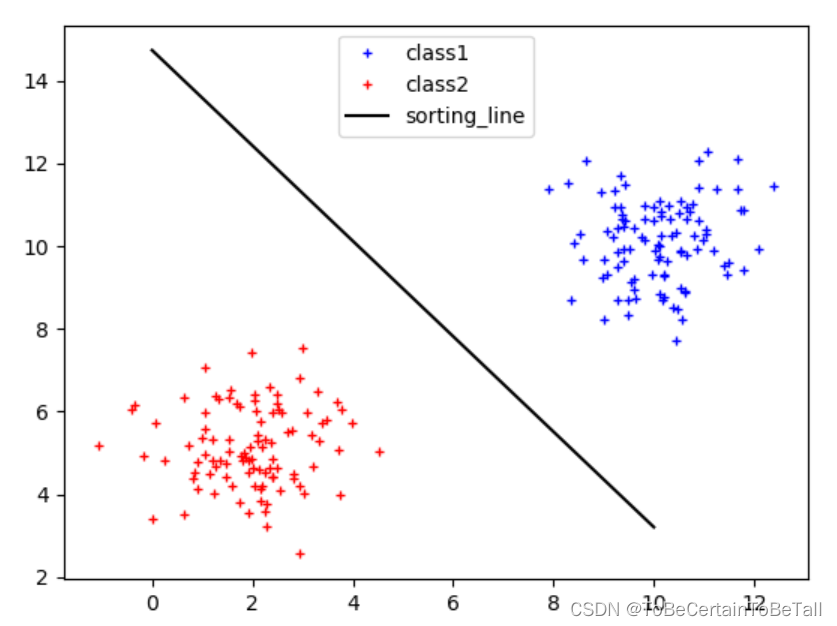
对于有两个特征的分类任务来说,我们的目的是寻找一条决策边界,使得这两个特征可以被区分开,如上图:
假设我们认为,决策边界为 A x 1 + B x 2 + C = 0 Ax_{1}+Bx_{2}+C = 0 Ax1+Bx2+C=0
当输入一个新数据 ( x 1 0 , x 2 0 ) (x_{1_{0}},x_{2_{0}}) (x10,x20)
对于蓝色特征(右上方)就会得到:A x 1 0 + B x 2 0 + C > 0 Ax_{1_{0}}+Bx_{2_{0}}+C > 0 Ax10+Bx20+C>0,即正样本
对于红色特征(左下方)就会得到:
A x 1 0 + B x 2 0 + C < 0 Ax_{1_{0}}+Bx_{2_{0}}+C < 0 Ax10+Bx20+C<0,即负样本
这里强调一点,对于分类任务:
A x 1 + B x 2 + C = 0 Ax_{1}+Bx_{2}+C = 0 Ax1+Bx2+C=0描述的不再是特征与结果之间的关系,而是特征与特征之间的关系
我们训练的目标,从将一个特征值带入方程来求另一个特征值变成了将两个特征值带入求 A x 1 + B x 2 + C = 0 Ax_{1}+Bx_{2}+C = 0 Ax1+Bx2+C=0的值
2. Logistic回归思想
Logistic回归算法并不满足于上述常规分类思想,而是在其基础上引入了概率的概念,即:
当输入一个新数据 ( x 1 0 , x 2 0 ) (x_{1_{0}},x_{2_{0}}) (x10,x20)
若该数据落在决策边界上:该样本点是正样本或负样本的概率都是0.5
若该数据落在决策边界左下方,且距离决策边界越远:
该样本点为负样本的概率越大,为正样本的概率越小
若该数据落在决策边界右上方,且距离决策边界越远:
该样本点为正样本的概率越大,为负样本的概率越小
上述描述中,不难看出,Logistic回归是将距离与概率进行关联,那么具体怎样实现呢?
首先我们定义Logistic函数: y = 1 1 + e − x y = \frac{1}{1+e^{-x} } y=1+e−x1
其中,x为样本点到决策边界的距离,即 A x 1 + B x 2 + C = 0 的值 Ax_{1}+Bx_{2}+C = 0的值 Ax1+Bx2+C=0的值
对于公式,简单解析下:
- 公式为什么会出现e?
求导方便
- 为什么公式中样本点到决策边界距离的计算方式与数学中不符?
数学中,点到直线的公式为 A x 0 + B y 0 + C A 2 + B 2 \frac{Ax_{0}+By_{0}+C }{\sqrt{A^{2}+ B^{2}} } A2+B2Ax0+By0+C,其中 A 2 + B 2 \sqrt{A^{2}+ B^{2}} A2+B2可以看作一个整数
公式中,我们求得的距离之所以没有除以 A 2 + B 2 \sqrt{A^{2}+ B^{2}} A2+B2,是因为每个点的相对距离是一样的
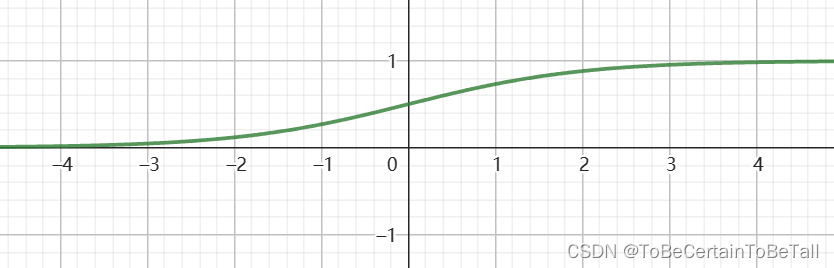
通过观察函数图像,我们可以看出这个函数非常符合Logistic回归思想:
自变量x:样本点到决策边界的距离d因变量y:样本点属于正负样本的概率P当自变量为0时,P=0.5当自变量趋近-∞时,P趋近于0当自变量趋近+∞时,P趋近取1【注意】这里的距离是有正有负的
由于Logistic函数的形状类似于S,所以该函数又被称为Sigmoid函数
二. Logistic回归算法:线性可分推导
下面我们来具体聊Logistic回归算法,但在开始之前,我们先来明确分类的种类:
对于二分类任务目标:我们需要寻找一个决策边界,从而达到将两类样本点区分的目的这里所谓的决策边界,即分类问题中进行分类决策的依据:对于二维空间,决策边界是一条直线对于三维空间,决策空间是一个平面对于多为空间,决策边界是一个超平面也就是说:当上面这些决策边界存在时,我们认为这些样本点是线性可分的当上面这些决策边界不存在时,我们认为这些样本点是线性不可分的;比如:找不到一条直线,将样本进行二分类这里补充一点:对于线性不可分的情况,我们的解决方法其实是多项式扩展
那么,接下来我们先来讨论二维空间中的线性可分问题
首先我们先用公式阐述我们的问题:
存在一条决策边界 f ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 = θ T X , f ( x ) 为距离 f(x)=\theta _{0} +\theta _{1}x_{1}+\theta _{2}x_{2} = \theta ^{T} X,f(x)为距离 f(x)=θ0+θ1x1+θ2x2=θTX,f(x)为距离
其中,令 g ( x ) = 1 1 + e − x , g ( x ) 为概率 g(x) = \frac{1}{1+e^{-x} },g(x)为概率 g(x)=1+e−x1,g(x)为概率
则,会得到 h θ ( x ) = g ( f ( x ) ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_{\theta } (x) = g(f(x))= g(\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2} ) hθ(x)=g(f(x))=g(θ0+θ1x1+θ2x2)
当确定 θ 0 , θ 1 , θ 2 \theta _{0},\theta _{1},\theta _{2} θ0,θ1,θ2后,就可以用 h θ ( x ) h_{\theta } (x) hθ(x)对新数据进行预测;需要注意的是,此时预测的是样本属于正样本的概率
结合上面对于问题的描述,我们开始对公式进行推导
假设我们采集到数据后,进行标注,得到数据集如下:
x 1 ( i ) , x 2 ( i ) , . . . , x N ( i ) , y ( i ) x_{1}^{(i)}, x_{2}^{(i)}, ... , x_{N}^{(i)}, y^{(i)} x1(i),x2(i),...,xN(i),y(i)
其中,数据集的正样本标注为 y ( i ) = 1 y^{(i)}=1 y(i)=1
其中,数据集的负样本标注为 y ( i ) = 0 y^{(i)}=0 y(i)=0
对于线性可分问题,存在决策边界为:
θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ N x N = 0 \theta _{0}+ \theta _{1}x_{1}+\theta _{2}x_{2}+ ... +\theta _{N}x_{N} = 0 θ0+θ1x1+θ2x2+...+θNxN=0
则,令
d = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ N x N ,这里的距离 d 有正负 d=\theta _{0}+ \theta _{1}x_{1}+\theta _{2}x_{2}+ ... +\theta _{N}x_{N},这里的距离d有正负 d=θ0+θ1x1+θ2x2+...+θNxN,这里的距离d有正负
如果带入每个样本的特征值,就会得到每个样本点到直线的距离,即:
d = θ 0 + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + . . . + θ N x N ( i ) d = \theta _{0}+ \theta _{1}x_{1}^{(i)}+\theta _{2}x_{2}^{(i)}+ ... +\theta _{N}x_{N}^{(i)} d=θ0+θ1x1(i)+θ2x2(i)+...+θNxN(i)
根据Logistic函数
y = 1 1 + e − x y = \frac{1}{1+e^{-x}} y=1+e−x1
带入关于 θ \theta θ的函数d,我们可以得到
h θ ( x ) = 1 1 + e − d ( θ ) h_{\theta } (x) = \frac{1}{1+e^{-d(\theta )}} hθ(x)=1+e−d(θ)1
注意:
此时计算的 h θ ( x ) h_{\theta } (x) hθ(x)结果是以正样本为依据,即所计算的样本属于 正样本/正类 的概率
同理,我们就会得到计算样本属于 负样本/负类 的概率
即
{ P ( y = 1 ∣ x ; θ ) = h θ ( x ) P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) \left\{\begin{matrix}P(y=1|x;\theta ) = h_{\theta }(x) \\P(y=0|x;\theta ) = 1-h_{\theta }(x) \end{matrix}\right. {P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
合并后,我们会得到
P ( y ∣ x ; θ ) = h θ ( x ) y [ 1 − h θ ( x ) ] 1 − y P(y|x;\theta ) = h_{\theta }(x)^{y}\left [ 1-h_{\theta }(x) \right ]^{1-y} P(y∣x;θ)=hθ(x)y[1−hθ(x)]1−y
这样,我们就可以得到关于 θ \theta θ的似然函数:
L ( θ ) = ∏ i = 1 M h θ ( x ( i ) ) y ( i ) [ 1 − h θ ( x ( i ) ) ] 1 − y ( i ) L(\theta)=\prod_{i=1}^{M} h_{\theta }(x^{(i)} )^{y^{(i)} }\left [ 1-h_{\theta }(x^{(i)}) \right ]^{1-y^{(i)}} L(θ)=i=1∏Mhθ(x(i))y(i)[1−hθ(x(i))]1−y(i)
为了方便计算,我们对似然求对数,得到
l ( θ ) = l n [ L ( θ ) ] = ∑ i = 1 M { y ( i ) l n [ h θ ( x ( i ) ) ] + ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] } l(\theta )=ln\left [ L(\theta)\right ]=\sum_{i=1}^{M}\left \{y^{(i)}ln[h_{\theta}(x^{(i)} )]+(1-y^{(i)})ln[1-h_{\theta}(x^{(i)} )] \right \} l(θ)=ln[L(θ)]=i=1∑M{y(i)ln[hθ(x(i))]+(1−y(i))ln[1−hθ(x(i))]}
下面,就到了我们熟悉的环节,求 θ \theta θ偏导
∂ l ( θ ) ∂ ( θ j ) = ∑ i = 1 M ∂ { y ( i ) l n [ h θ ( x ( i ) ) ] + ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] } ∂ ( θ j ) \frac{\partial l(\theta )}{\partial (\theta _{j} )} =\sum_{i=1}^{M}\frac{\partial\left \{ y^{(i)}ln[h_{\theta}(x^{(i)} )]+(1-y^{(i)})ln[1-h_{\theta}(x^{(i)} )] \right \} }{\partial(\theta _{j})} ∂(θj)∂l(θ)=∑i=1M∂(θj)∂{y(i)ln[hθ(x(i))]+(1−y(i))ln[1−hθ(x(i))]}
= ∑ i = 1 M ( y ( i ) h θ ( x ( i ) ) − 1 − y ( i ) 1 − h θ ( x ( i ) ) ) ∂ ( h θ ( x ( i ) ) ) ∂ ( θ j ) =\sum_{i=1}^{M}( \frac{y^{(i)}}{h_{\theta}(x^{(i)})} -\frac{1-y^{(i)}}{1-h_{\theta}(x^{(i)})})\frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )} =∑i=1M(hθ(x(i))y(i)−1−hθ(x(i))1−y(i))∂(θj)∂(hθ(x(i)))
这里我们来推导 ∂ ( h θ ( x ( i ) ) ) ∂ ( θ j ) \frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )} ∂(θj)∂(hθ(x(i)))
其中, h θ ( x ) = 1 1 + e − d ( θ ) h_{\theta } (x) = \frac{1}{1+e^{-d(\theta )}} hθ(x)=1+e−d(θ)1,又 y = 1 1 + e − x y = \frac{1}{1+e^{-x}} y=1+e−x1所以我们先对y进行求导
d y d x = [ − 1 ( 1 + e − x ) 2 ∗ e − x ∗ ( − 1 ) ] \frac{\mathrm{d} y}{\mathrm{d} x} =\left [ -\frac{1}{(1+e^{-x} )^{2}}\ast e^{-x}\ast (-1)\right ] dxdy=[−(1+e−x)21∗e−x∗(−1)]
= 1 1 + e − x ∗ e − x 1 + e − x = \frac{1}{1+e^{-x}} \ast \frac{e^{-x}}{1+e^{-x}} =1+e−x1∗1+e−xe−x
= 1 1 + e − x ∗ ( 1 − 1 1 + e − x ) =\frac{1}{1+e^{-x}} \ast (1-\frac{1}{1+e^{-x}}) =1+e−x1∗(1−1+e−x1)
= y ∗ ( 1 − y ) =y \ast (1-y) =y∗(1−y)对于 ∂ ( h θ ( x ( i ) ) ) ∂ ( θ j ) \frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )} ∂(θj)∂(hθ(x(i)))我们就会得到
∂ ( h θ ( x ( i ) ) ) ∂ ( θ j ) = h θ ( x ( i ) ) ∗ [ 1 − h θ ( x ( i ) ) ] ∗ ∂ d ( θ ) ∂ θ j \frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )}=h_{\theta}(x^{(i)})\ast \left [ 1-h_{\theta}(x^{(i)}) \right ] \ast \frac{\partial d(\theta )}{\partial \theta _{j} } ∂(θj)∂(hθ(x(i)))=hθ(x(i))∗[1−hθ(x(i))]∗∂θj∂d(θ)
∂ l ( θ ) ∂ θ j = ∑ i = 1 M ( y ( i ) h θ ( x ( i ) ) − 1 − y ( i ) 1 − h θ ( x ( i ) ) ) ∂ ( h θ ( x ( i ) ) ) ∂ θ j \frac{\partial l(\theta )}{\partial \theta _{j} }=\sum_{i=1}^{M}( \frac{y^{(i)}}{h_{\theta}(x^{(i)})} -\frac{1-y^{(i)}}{1-h_{\theta}(x^{(i)})})\frac{\partial(h_{\theta}(x^{(i)})) }{\partial \theta _{j} } ∂θj∂l(θ)=∑i=1M(hθ(x(i))y(i)−1−hθ(x(i))1−y(i))∂θj∂(hθ(x(i)))
= ∑ i = 1 M ( y ( i ) h θ ( x ( i ) ) − 1 − y ( i ) 1 − h θ ( x ( i ) ) ) ∗ h θ ( x ( i ) ) ∗ [ 1 − h θ ( x ( i ) ) ] ∗ ∂ d ( θ ) ( i ) ∂ θ j =\sum_{i=1}^{M}( \frac{y^{(i)}}{h_{\theta}(x^{(i)})} -\frac{1-y^{(i)}}{1-h_{\theta}(x^{(i)})})\ast h_{\theta}(x^{(i)})\ast \left [ 1-h_{\theta}(x^{(i)}) \right ] \ast \frac{\partial d(\theta )^{(i)} }{\partial \theta _{j} } =∑i=1M(hθ(x(i))y(i)−1−hθ(x(i))1−y(i))∗hθ(x(i))∗[1−hθ(x(i))]∗∂θj∂d(θ)(i)
= ∑ i = 1 M [ y ( i ) − h θ ( x ( i ) ) ] ∗ ∂ d ( θ ) ( i ) ∂ θ j =\sum_{i=1}^{M}[y^{(i)}-h_{\theta}(x^{(i)} ) ] \ast \frac{\partial d(\theta )^{(i)} }{\partial \theta _{j} } =∑i=1M[y(i)−hθ(x(i))]∗∂θj∂d(θ)(i)
根据 d ( θ ) ( i ) = θ 0 x 0 ( i ) + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + . . . + θ N x N ( i ) d(\theta )^{(i)} = \theta _{0}x_{0}^{(i)}+ \theta _{1}x_{1}^{(i)}+\theta _{2}x_{2}^{(i)}+ ... +\theta _{N}x_{N}^{(i)} d(θ)(i)=θ0x0(i)+θ1x1(i)+θ2x2(i)+...+θNxN(i)
我们可以得到
∂ d ( θ ) ( i ) ∂ θ j = x j ( i ) \frac{\partial d(\theta )^{(i)} }{\partial \theta _{j} }=x_{j}^{(i)} ∂θj∂d(θ)(i)=xj(i)
∂ l ( θ ) ∂ θ j = ∑ i = 1 M [ y ( i ) − h θ ( x ( i ) ) ] ∗ x j ( i ) \frac{\partial l(\theta )}{\partial \theta _{j} }=\sum_{i=1}^{M}[y^{(i)}-h_{\theta}(x^{(i)} ) ] \ast x_{j}^{(i)} ∂θj∂l(θ)=i=1∑M[y(i)−hθ(x(i))]∗xj(i)
为了求解似然函数的最大值,我们需要令导数等于0,即
∂ l ( θ ) ∂ θ j = 0 \frac{\partial l(\theta )}{\partial \theta _{j} }=0 ∂θj∂l(θ)=0
这里继续向下推会发现,求解偏导为0的计算十分困难
由此,我们会想到用梯度下降优化模型参数,那么,具体怎么优化,我们下一篇再见啦!
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
祝愉快🌟!
相关文章:

分类问题经典算法 | 二分类问题 | Logistic回归:公式推导
目录 一. Logistic回归的思想1. 分类任务思想2. Logistic回归思想 二. Logistic回归算法:线性可分推导 一. Logistic回归的思想 1. 分类任务思想 分类问题通常可以分为二分类,多分类任务;而对于不同的分类任务,训练的主要目标是…...
redis实现分布式全局唯一id
目录 一、前言二、如何通过Redis设计一个分布式全局唯一ID生成工具2.1 使用 Redis 计数器实现2.2 使用 Redis Hash结构实现 三、通过代码实现分布式全局唯一ID工具3.1 导入依赖配置3.2 配置yml文件3.3 序列化配置3.4 编写获取工具3.5 测试获取工具 四、运行结果 一、前言 在很…...

Sora引发安全新挑战
文章目录 前言一、如何看待Sora二、Sora加剧“深度伪造”忧虑三、Sora无法区分对错四、滥用导致的安全危机五、Sora面临的安全挑战总结前言 今年2月,美国人工智能巨头企业OpenAI再推行业爆款Sora,将之前ChatGPT以图文为主的生成式内容全面扩大到视频领域,引发了全球热议,这…...

Android 14.0 Launcher3定制化之桌面分页横线改成圆点显示功能实现
1.前言 在14.0的系统rom产品定制化开发中,在进行launcher3的定制化中,在双层改为单层的开发中,在原生的分页 是横线,而为了美观就采用了系统原来的另外一种分页方式,就是圆点比较美观,接下来就来分析下相关…...
SemiDrive E3 MCAL 开发系列(3)– Wdg 模块的使用
一、 概述 本文将会介绍 SemiDrive E3 MCAL Wdg 模块的基本配置,并且会结合实际操作的介绍,帮助新手快速了解并掌握这个模块的使用,文中的 MCAL 是基于 PTG3.0 的版本,开发板是官方的 E3640 网关板。 二、 Wdg 模块的主要配置 …...

AI推荐算法的演进之路
推荐算法 基于大数据和AI技术,提供全流程一站式推荐平台,协助企业构建个性化推荐应用,提升企业应用的点击率留存率和永久体验。目前,主要的推荐方法包括:基于内容推荐、协同过滤推荐、基于关联规则推荐、基于效用推荐…...
Tomcat安装,配置文件、组件
一、Tomcat的基本功能 1.1.Tomcat是什么? Tomcat服务器是一个免费的开放源代码的Web应用服务器,属于轻量级应用服务器,在中小型系统和并发访问用户不是很多的场合下被普遍使用,是开发和调试JSP程序的首选。一般来说,T…...

精读《React Hooks 最佳实践》
简介 React 16.8 于 2019.2 正式发布,这是一个能提升代码质量和开发效率的特性,笔者就抛砖引玉先列出一些实践点,希望得到大家进一步讨论。 然而需要理解的是,没有一个完美的最佳实践规范,对一个高效团队来说&#x…...

varFormatter 数据格式化库 以性能优先的 快速的 内存对象格式转换
varFormatter 数据格式化 技术 开源技术栏 对象/变量格式化工具库,其支持将一个对象进行按照 JSON XML HTML 等格式进行转换,并获取到结果字符串! 目录 文章目录 varFormatter 数据格式化 技术目录介绍获取方式 使用实例格式化组件的基本使…...
基于PHP的在线英语学习平台
有需要请加文章底部Q哦 可远程调试 基于PHP的在线英语学习平台 一 介绍 此在线英语学习平台基于原生PHP开发,数据库mysql。系统角色分为学生,教师和管理员。(附带参考设计文档) 技术栈:phpmysqlphpstudyvscode 二 功能 学生 1 注册/登录/…...
答辩常规问题和如何回答(答辩指导))
基于微信小程序电影院订票选座系统 (后台JSP+JDBC+Mysql)答辩常规问题和如何回答(答辩指导)
博主介绍:黄菊华老师《Vue.js入门与商城开发实战》《微信小程序商城开发》图书作者,CSDN博客专家,在线教育专家,CSDN钻石讲师;专注大学生毕业设计教育和辅导。 所有项目都配有从入门到精通的基础知识视频课程ÿ…...
:模拟算法真题 ★★★☆☆《安全警报》)
C++知识点总结(22):模拟算法真题 ★★★☆☆《安全警报》
安全警报 1. 审题 题目描述 Z市最大的金融公司:太平洋金融遭到了入侵,一名黑客潜入到了公司中,公司紧急启动安保程序,将大楼封锁,并安排作为安全主管的你对楼层进行搜查。所以你准备写一个程序,输入搜查楼…...

蓝桥杯练习系统(算法训练)ALGO-993 RP大冒险
资源限制 内存限制:64.0MB C/C时间限制:200ms Java时间限制:600ms Python时间限制:1.0s 问题描述 请尽情使用各种各样的函数来测试你的RP吧~~~ 输入格式 一个数N表示测点编号。 输出格式 一个0~9的数。 样例输入 0 样…...
Unity的相机跟随和第三人称视角
Unity相机跟随和第三人称视角 介绍镜头视角跟随人物方向进行旋转的镜头视角固定球和人的镜头视角 思路跟随人物方向进行旋转的镜头视角固定球和人的镜头视角 镜头旋转代码人物移动的参考代码注意 介绍 最近足球项目的镜头在做改动,观察了一下实况足球的视角&#x…...

哪个超声波清洗机品牌值得入手?销量榜品牌值得选购!
在科技日益发展的今天,超声波清洗技术以其高效、便捷和深度清洁的特点,已经深入到生活的诸多领域,从精密仪器到珠宝首饰,从眼镜框到假牙,甚至是厨房用品的日常护理,都能见到超声波清洗机的身影。面对市场上…...

Stwo:基于Circle STARK和M31的下一代STARK证明系统
1. 引言 StarkWare团队和Polygon Labs团队,历时数月,构造了基于Mersenne素数域M31的Circle STARK协议,通过使用M31 over a circle,可基于任意有限域构造高效STARKs,具体见2024年2月19日论文《Circle STARKs》。 基于…...
)
笔记本以太网集线器Hub充电可能导致网络异常(貌似是我把服务器网关写错了)
文章目录 笔记本以太网集线器(Hub)充电导致网络异常概述原理分析电源与信号干扰设备热度设备兼容性问题 解决方案升级固件提高设备散热效率选择兼容性好的设备 总结 今天用笔记本以太网直连服务器,一开始能连通,结果以太网hub插上…...

npm ERR! code ETIMEDOUT
在新建vue项目的时候报错 npm ERR! code ETIMEDOUT npm ERR! syscall connect npm ERR! errno ETIMEDOUT npm ERR! network request to https://registry.npmjs.org/vue%2fcli failed, reason: connect ETIMEDOUT 104.16.2.35:443 npm ERR! network This is a problem relate…...
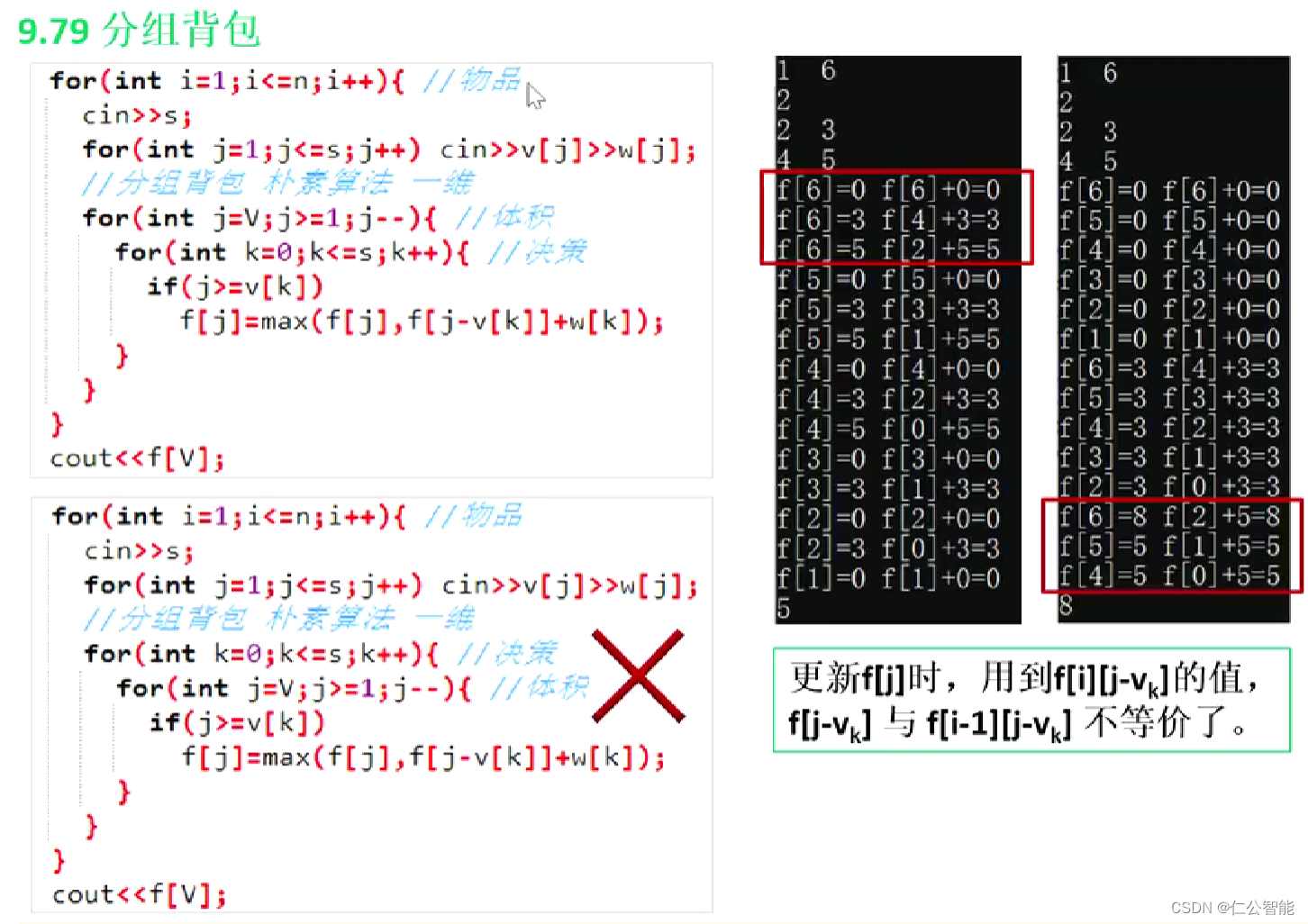
动态规划(算法竞赛、蓝桥杯)--分组背包DP
1、B站视频链接:E16 背包DP 分组背包_哔哩哔哩_bilibili #include <bits/stdc.h> using namespace std; const int N110; int v[N][N],w[N][N],s[N]; // v[i,j]:第i组第j个物品的体积 s[i]:第i组物品的个数 int f[N][N]; // f[i,j]:前i组物品,能放…...

太阳能供电井盖-物联网智能井盖监测系统-旭华智能
在这个日新月异的科技时代,城市的每一个角落都在悄然发生变化。而在这场城市升级的浪潮中,智能井盖以其前瞻性的科技应用和卓越的安全性能,正悄然崭露头角,变身马路上的智能“眼睛”,守护城市安全。 传统的井盖监测系统…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
