13_pinctrl子系统
总结
pinctrl作为驱动
iomuxc节点在设备树里面 存储全部所需的引脚配置信息
iomux节点匹配pinctrl子系统
控制硬件外设的时候 要知道有哪些gpio 再看gpio有哪些服用寄存器
接着在程序配置gpio相关寄存器 这样搞效率很低
所以用iomux节点保存所有的引脚组 pinctrl驱动起来的时候获得所有引脚信息 保存在内存
pinctrl子系统预先确定引脚的数量和名字
- 为每个引脚的配置信息分配内存
- pinctrl子系统统一管理每个引脚的使用状态
-iomux节点存放了各种引脚属性,pinctrl驱动解析iomux节点,存放引脚信息进入内存
iomux节点里如何填写
//iomuxc节点
//imx6ull.dtsi
iomuxc: iomuxc@20e0000 {compatible = "fsl,imx6ul-iomuxc";reg = <0x20e0000 0x4000>;};
//继续扩展 引用iomux节点 **imx6ull-seeed-npi.dts**
&iomuxc {pinctrl-names = "default","init","sleep"; //选定引脚状态pinctrl-0 = <&pinctrl_uart1>; //一个状态就是一组引脚,比如对应下面pinctrl-1 =<&xxx>;pinctrl-2 =<&yyy>;
...pinctrl_uart1: uart1grp {fsl,pins = <MX6UL_PAD_UART1_TX_DATA__UART1_DCE_TX 0x1b0b1MX6UL_PAD_UART1_RX_DATA__UART1_DCE_RX 0x1b0b1>;};...
}
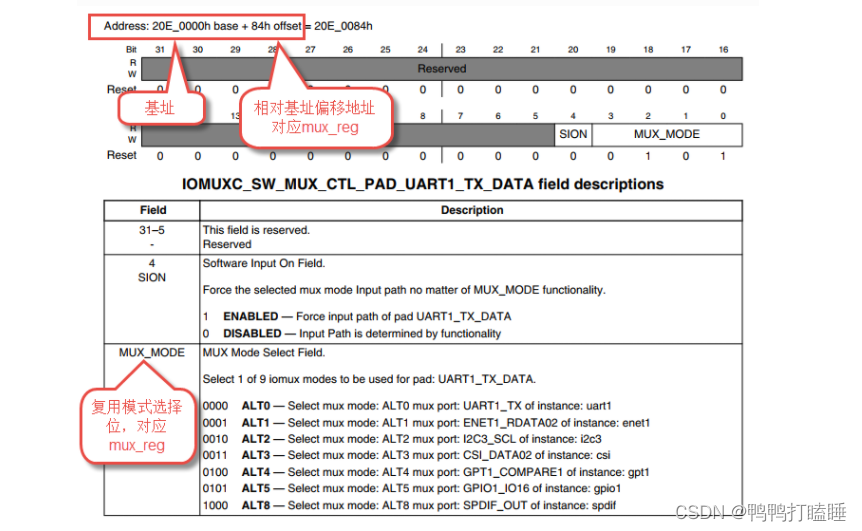
上面 引脚里面的宏是什么意思
MX6UL_PAD_UART1_TX_DATA__UART1_DCE_TX
#define MX6UL_PAD_UART1_TX_DATA__UART1_DCE_TX 0x0084 0x0310 0x0000 0 0
< mux_reg conf_reg input_reg mux_mode input_val >0x0084 0x0310 0x0000 0x0 0x0
mux_reg:引脚复用设置寄存器 基地址+mux_reg 就是 PIN 的复用寄存器地址。
conf_reg : 设置这个引脚的电气属性的寄存器地址 基地址+conf_reg =设置pin的电气属性地址
input_reg:引脚输入设置寄存器 有些外设有 input_reg 寄存器
引脚需要输入功能时设置
mux_mode:复用寄存器设置值
设置引脚复用
input_val:输入寄存器设置值
设置引脚输入特性
宏的最后跟随了一串数字 用来设置PIN的电气属性值 比如IO 的上/下拉、驱动能力和速度等

引脚状态初始化
在设备树里面节点 会变成plantform_dev 会执行probe进行匹配驱动
但是执行probe和drv配对之前 先回执行really_porbe() 这个函数和下面的引脚状态关系很大
用来初始化引脚值
//iomuxc节点
//imx6ull.dtsi
iomuxc: iomuxc@20e0000 {compatible = "fsl,imx6ul-iomuxc";reg = <0x20e0000 0x4000>;};
//继续扩展 引用iomux节点 **imx6ull-seeed-npi.dts**
&iomuxc {pinctrl-names = "default","init","sleep"; //选定引脚状态pinctrl-0 = <&pinctrl_uart1>; //一个状态就是一组引脚,比如对应下面pinctrl-1 =<&xxx>;pinctrl-2 =<&yyy>;
...pinctrl_uart1: uart1grp {fsl,pins = <MX6UL_PAD_UART1_TX_DATA__UART1_DCE_TX 0x1b0b1MX6UL_PAD_UART1_RX_DATA__UART1_DCE_RX 0x1b0b1>;};...
}
还是用上一个设备树举例 看了下面的例子
就知道驱动的引脚其实在 probe之前就已经初始化好了电气属性了
drivers/base/dd.c
static int really_probe(struct device *dev, struct device_driver *drv)
{int ret = -EPROBE_DEFER;
...
re_probe:dev->driver = drv;ret = pinctrl_bind_pins(dev); //这里根据iomux节点的 几个引脚状态来初始化引脚组
...if (dev->bus->probe) {ret = dev->bus->probe(dev);if (ret)goto probe_failed;} else if (drv->probe) {ret = drv->probe(dev); //这个是熟悉的probeif (ret)goto probe_failed;}...}
int pinctrl_bind_pins(struct device *dev)dev->pins->default_state = pinctrl_lookup_state(dev->pins->p,PINCTRL_STATE_DEFAULT);//从设备节点状态找到指定状态//本次是default状态dev->pins->init_state = pinctrl_lookup_state(dev->pins->p,PINCTRL_STATE_INIT); /这次找init状态if (IS_ERR(dev->pins->init_state))pinctrl_select_state(dev->pins->p,dev->pins->default_state);//没有init状态变成default状态elseret = pinctrl_select_state(dev->pins->p, dev->pins->init_state);//有的话引脚变成init状态相关文章:

13_pinctrl子系统
总结 pinctrl作为驱动 iomuxc节点在设备树里面 存储全部所需的引脚配置信息 iomux节点匹配pinctrl子系统 控制硬件外设的时候 要知道有哪些gpio 再看gpio有哪些服用寄存器 接着在程序配置gpio相关寄存器 这样搞效率很低 所以用iomux节点保存所有的引脚组 pinctrl驱动起来的时…...

Linux系统对于实施人员的价值
Linux系统对于实施人员的价值 随着互联网的发展,linux系统越来越突显了巨大的作用,很多互联网公司,政府企业,只要用到服务器的地方几乎都能看到linux系统的身影,可以说服务是不是在linux系统跑的代表了企业的技术水平&…...

ForkJoin 和 Stream并行流
还在用 for 循环计算两个数之间所有数的和吗?下面提供两种新方法! 1. ForkJoin 1.1 背景 要知道,在一个方法中,如果没有做特殊的处理,那么在方法开始到结束使用的都是同一个线程,无论你的业务有多复杂 那…...

逻辑优化-cofactor
1. 简介 逻辑综合中的Cofactor优化方法是一种重要的逻辑优化技术。它通过提取逻辑电路中的共同部分,从而简化电路、减小面积和延迟。该方法广泛应用于电子设计自动化(EDA)领域中的逻辑综合、等价转换和优化等方面。 Cofactor优化方法最早由…...

车道线检测CondLaneNet论文和源码解读
CondLaneNet: a Top-to-down Lane Detection Framework Based on Conditional Convolution Paper:https://arxiv.org/pdf/2105.05003.pdf code:GitHub - aliyun/conditional-lane-detection 论文解读: 一、摘要 这项工作作为车道线检测任…...

vue3的插槽slots
文章目录普通插槽Test.vueFancyButton.vue具名插槽Test.vueBaseLayout.vue作用域插槽默认插槽Test.vueBaseLayout.vue具名作用域插槽Test.vueBaseLayout.vue普通插槽 父组件使用子组件时,在子组件闭合标签中提供内容模板,插入到子组件定义的出口的地方 …...

docker学校服务器管理
docker 学校服务器管理使用docker,docker使用go语言编写。对于docker的理解,需要知道几个关键字docker, scp,images, container。 docker-码头工人scp-传输命令images/repository-镜像container-容器 docker是码头工人,scp相当…...
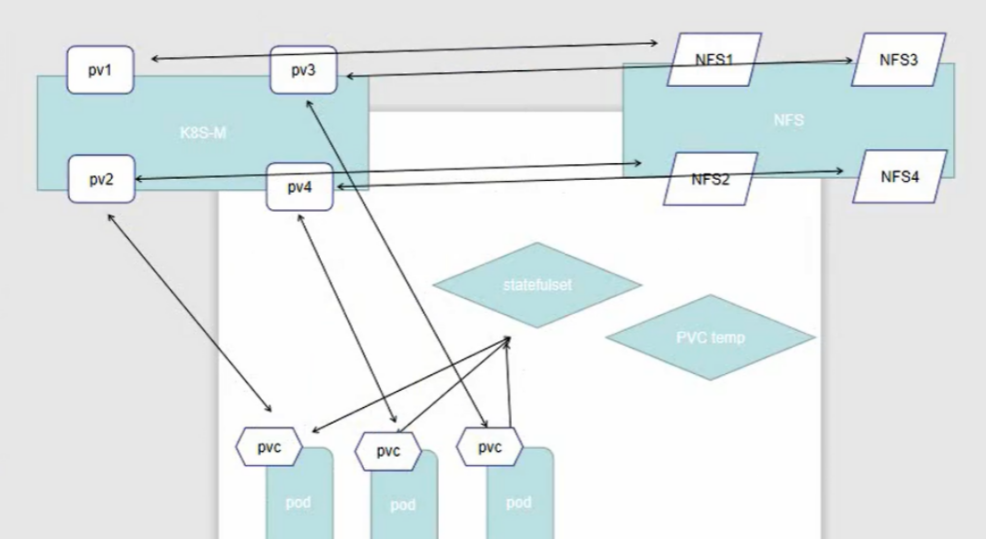
pv和pvc
一、PV和PVC详解当前,存储的方式和种类有很多,并且各种存储的参数也需要非常专业的技术人员才能够了解。在Kubernetes集群中,放了方便我们的使用和管理,Kubernetes提出了PV和PVC的概念,这样Kubernetes集群的管理人员就…...

k8s篇之Pod 干预与 PDB
文章目录自愿干预和非自愿干预PDBPDB 示例分离集群所有者和应用程序所有者角色如何在集群上执行中断操作自愿干预和非自愿干预 Pod 不会消失,除非有人(用户或控制器)将其销毁,或者出现了不可避免的硬件或软件系统错误。 我们把这…...
Django学习17 -- ManytoManyField
1. ManyToManyField (参考:Django Documentation Release 4.1.4) 类定义 class ManyToManyField(to, **options)使用说明 A many-to-many relationship. Requires a positional argument: the class to which the model is related, which w…...

既然有MySQL了,为什么还要有Redis?
目录专栏导读一、同样是缓存,用map不行吗?二、Redis为什么是单线程的?三、Redis真的是单线程的吗?四、Redis优缺点1、优点2、缺点五、Redis常见业务场景六、Redis常见数据类型1、String2、List3、Hash4、Set5、Zset6、BitMap7、Bi…...
RSTP基础要点(上)
RSTP基础RSTP引入背景STP所存在的问题RSTP对于STP的改进端口角色重新划分端口状态重新划分快速收敛机制:PA机制端口快速切换边缘端口的引入RSTP引入背景 STP协议虽然能够解决环路问题,但是由于网络拓扑收敛较慢,影响了用户通信质量ÿ…...
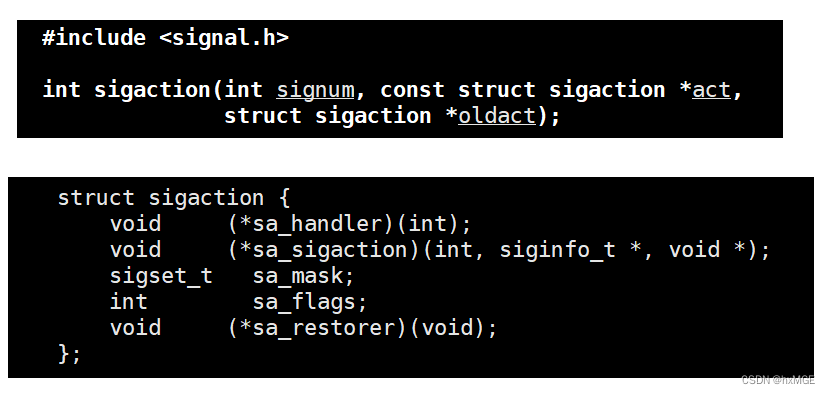
Linux操作系统学习(信号处理)
文章目录进程信号信号的产生方式(信号产生前)1. 硬件产生2.调用系统函数向进程发信号3.软件产生4.定位进程崩溃的代码(进程异常退出产生信号)信号保存的方式(信号产生中)获取pending表&&修改block表…...
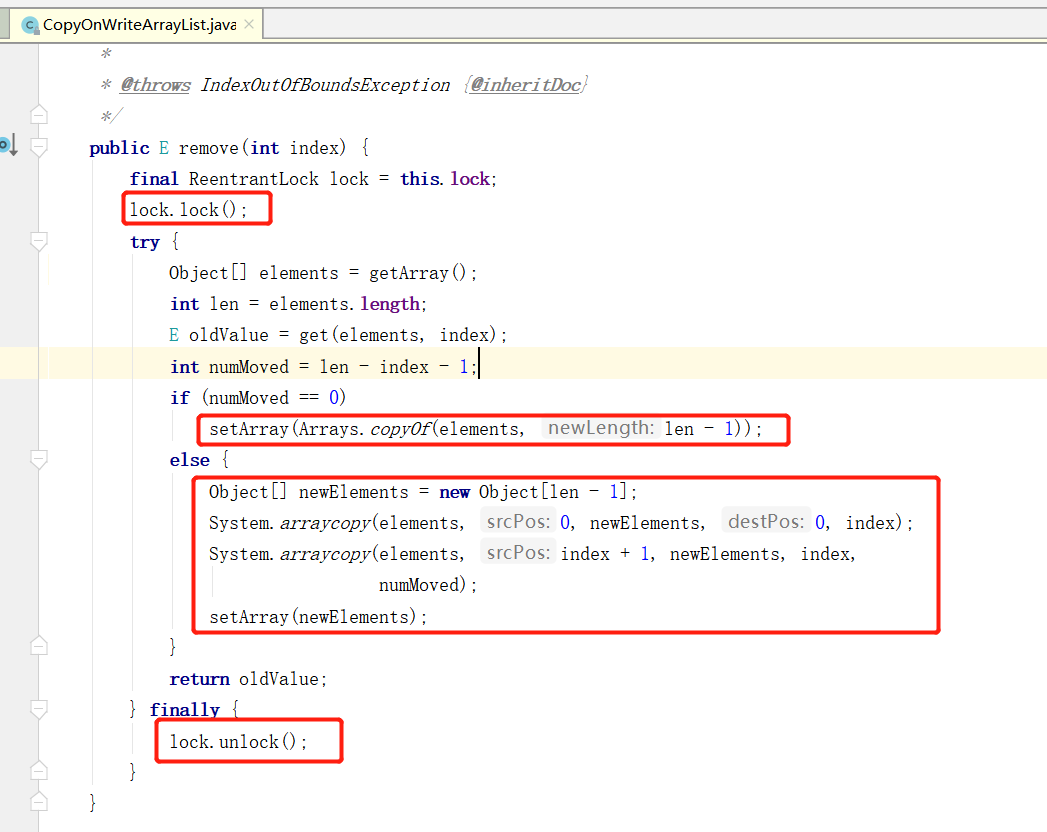
CopyOnWriteArrayList 源码解读
一、CopyOnWriteArrayList 源码解读 在 JUC 中,对于 ArrayList 的线程安全用法,比较推崇于使用 CopyOnWriteArrayList ,那 CopyOnWriteArrayList是怎么解决线程安全问题的呢,本文带领大家一起解读下 CopyOnWriteArrayList 的源码…...

方法
方法方法(函数)一、课前问答二、方法和函数三、方法的参数3.1 单个参数3.2 多个参数四、方法的返回值五、方法的多级调用六、递归方法(函数) 一、课前问答 1、break和continue的区别 2、嵌套循环的执行流程 3、二进制有哪些运算&…...
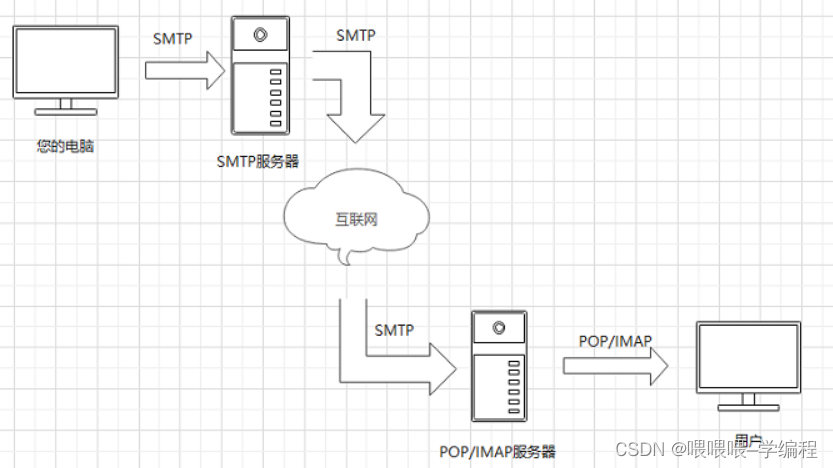
C/C++实现发送邮件功能(附源码)
C++常用功能源码系列 本文是C/C++常用功能代码封装专栏的导航贴。部分来源于实战项目中的部分功能提炼,希望能够达到你在自己的项目中拿来就用的效果,这样更好的服务于工作实践。 专栏介绍:专栏讲本人近10年后端开发常用的案例,以高质量的代码提取出来,并对其进行了介绍。…...

Java虚拟机JVM-运行时数据区域说明
及时编译器 HotSpot虚拟机中含有两个即时编译器,分别是编译耗时短但输出代码优化程度较低的客户端编译器(简称为C1)以及编译耗时长但输出代码优化质量也更高的服务端编译器(简称为C2),通常它们会在分层编译…...

修复电子管
年前在咸鱼捡漏买到了10根1G4G电子管,这是一种直热三极管,非常的少见。买回来的时候所有的灯丝都是通的,卖家说都是新的,库存货,但是外观实在是太糟糕了,看着就像被埋在垃圾场埋了几十年的那种,…...
【Java】反射机制和代理机制
目录一、反射1. 反射概念2. 反射的应用场景3. 反射机制的优缺点4. 反射实战获取 Class 对象的四种方式二、代理机制1. 代理模式2. 静态代理3. 动态代理3.1 JDK动态代理机制1. 介绍2.JDK 动态代理类使用步骤3. 代码示例3.2 CGLIB 动态代理机制1.介绍2.CGLIB 动态代理类使用步骤3…...

synchronized底层
Monitor概念一、Java对象头二、Monitor2.1、Monitor—工作原理2.2、Monitor工作原理—字节码角度2.2、synchronized进阶原理(优化)2.3、synchronized优化原理——轻量级锁2.4、synchronized优化原理——锁膨胀2.5、synchronized优化原理——自旋优化2.6、…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
