浅谈密码学
文章目录
- 每日一句正能量
- 前言
- 什么是密码学
- 对称加密简述
- 加密语法
- Kerckhoffs原则
- 常用的加密算法
- 现代密码学的原则
- 威胁模型(按强度增加的顺序)
- 密码学的应用领域
- 后记

每日一句正能量
人生在世,谁也不能做到让任何人都喜欢,所以没必要去讨好别人,更不必纠结于别人对自己的评价,珍惜那些珍惜自己的人,忽略哪些忽略我们的人,做自己喜欢的自己就好。
前言
密码学作为一门研究信息安全的学科,扮演着保护我们数字化生活的重要角色。在当今信息时代,我们的个人和商业数据面临着越来越多的威胁,如黑客攻击、数据泄露等。而密码学的出现为我们提供了一种科学的方法,能够确保我们的信息在传输和存储过程中不被未授权的人访问和篡改。本文将简要介绍密码学的基本原理和应用领域,以及其在保护数字化生活中的重要性。通过了解密码学的基础知识,我们将能更好地保护个人隐私和敏感信息,建立一个安全可信的网络环境。
什么是密码学
密码学是研究编制密码和破译密码的技术科学。研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。电报最早是由美国的摩尔斯在1844年发明的,故也被叫做摩尔斯电码。它由两种基本信号和不同的间隔时间组成:短促的点信号 .,读 的 (Di);保持一定时间的长信号—,读答 (Da)。间隔时间:滴,1t;答,3t;滴答间,1t;字母间,3t;字间,5t。
引用自百度百科
官方定义:密码学是研究编制密码和破译密码的技术科学。研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。
通俗理解:密码学是隐藏信息的科学和艺术,因此它们是保密的,然后"取消隐藏"它们,以便只有预期的接收者才能阅读它们。基本上,我们可以说密码学是秘密消息传递的科学。
对称加密简述
经典密码学关注的是对密码的设计和使用,使得在有第三方窃听者监听消息的情况下,双方能够发送消息而不被监听者看到。监听者可以监视他们之间的所有消息。上面所说的“密码”就是后面我们要说的“加密方案”。所有经典密码学的安全性都依赖于一个秘密——密钥 (key)——由通信双方提前生成并交换而窃听者无法获取。这种方式就是private-key encryption。
在密码学中,我们将加密方案分为private-key (symmetric) encryption和public-key (asymmetric) encryption。
在private-key encryption中,当通信双方想要秘密通信的时候,提前交换一个key。其中一方可以使用这个key来加密一条消息,或者叫明文 (plaintext),然后发送给另一方。因此可以说,其中一方将一个密文ciphertext发送给了另一方。接收者使用key解密这个密文,得到了原始消息。这里的key都是相同的,并且用于明文和密文之间的转换。这也是为什么人们将之称为symmetric encryption。然而asymmetric encryption与之相反,其加密和解密使用的是不同的key。
加密语法
正式地,一个private-key encryption方案由一个消息空间M和三个算法 (Gen 、Enc和Dec) 组成。
-
Gen:密钥生成算法
-
Enc:加密算法
-
Dec:解密算法
这三个算法的功能描述如下:
-
Gen是一个概率算法,根据某种分布,输出一个密钥k。
-
Enc将一个密钥k和一个明文消息m作为输入,输出一个密文c,即Enck(m)表示用密钥k对明文消息m进行加密。
-
Dec将一个密钥k和一个密文c作为输入,输出一个明文消息m。即Deck©表示用密钥k对密文消息c进行解密。
所有由Gen生成的密钥k组成了一个密钥空间,记为K。由Dec生成的密文c 组成了一个明文空间,记为C。
一个加密方案必须满足如下确定性要求:对于每一个由Gen输出的密钥k和每一个明文消息m∈M,Deck (Enck(m) = m
对称加密流程:运行Gen来生成密钥k,当一方想要发送明文消息m给另一方时,
他计算c : = Enck(m),
然后在公开信道中将密文c发送给对方。
接收者收到密文c后,
计算m : = Deck©来得到原始消息。
“ := ”表示确定性等式,假设此处的Enc是确定性的,Enc是概率性的算法
Kerckhoffs原则
“加密方案没有必要保密,它可以被敌人轻易获得。”
也就是说,即使窃听者知道加密方案的所有细节,只要攻击者不知道正在使用的密钥k,这个加密方案应该是安全的。故,Kerckhoffs的原则要求安全性仅仅依赖于密钥k的保密。
理由:
-
保密一个密钥k比保密一个相对复杂的加密方案更加容易,尤其是在加密方案被广泛使用的情况下。
-
如果诚实方共享的秘密信息被泄漏,更换密钥比更换加密方案容易得多。此外,生成一个新的随机密钥是相对简单的,而设计一个新的加密方案则是一个巨大的工程。
-
在广泛部署加密方案之前,鼓励公众对该方案进行审查以检查可能存在的弱点,这是一个显著的好处。进一步地,标准化加密方案可以确保不同用户之间的兼容性,公众将使用经过公开审查的强大的加密方案。这更加令人信服。
故,广泛、公开地传播加密方案的全部细节是有利的。
常用的加密算法
常用的加密算法包括以下几种:
-
对称加密算法:对称加密算法使用相同的密钥来进行加密和解密。常见的对称加密算法有DES(Data Encryption Standard)、AES(Advanced Encryption Standard)和3DES(Triple Data Encryption Algorithm)。
-
非对称加密算法:非对称加密算法使用一对密钥,一个是公钥用于加密,另一个是私钥用于解密。常见的非对称加密算法有RSA(Rivest-Shamir-Adleman)、Diffie-Hellman和ECC(Elliptic Curve Cryptography)。
-
散列算法:散列算法将任意长度的数据转换为定长的哈希值。常见的散列算法有MD5(Message Digest 5)、SHA-1(Secure Hash Algorithm 1)、SHA-256等。
-
数字签名算法:数字签名算法使用私钥对消息进行签名,以确保消息的完整性、认证性和不可否认性。常见的数字签名算法有RSA、DSA(Digital Signature Algorithm)和ECDSA(Elliptic Curve Digital Signature Algorithm)。
-
密码哈希函数:密码哈希函数是对输入的密码进行哈希运算,以便在存储密码时保护用户的隐私。常见的密码哈希函数有bcrypt、PBKDF2(Password-Based Key Derivation Function 2)和scrypt。
这些加密算法在不同的应用场景中有不同的优势和适用性,选择适合的加密算法取决于安全需求和性能要求。
现代密码学的原则
-
原则一:形式化定义:明确“安全”到底是什么意思
-
原则二:精确的假设:事实证明,大多数密码证明依赖于关于某些数学问题的算法难度的目前未被证明的假设
-
原则三:安全性证明:任何这样的假设都必须明确并精确地陈述。
安全的加密方案应该保证:不管攻击者已经拥有什么信息,密文都不应该泄露关于底层明文的额外信息。
威胁模型(按强度增加的顺序)
-
唯密文攻击(Ciphertext-only attack):敌手只观察一个密文(或多个密文),并试图确定关于底层明文(或多个明文)的信息。
-
已知明文攻击(Known-plaintext attack):在这里,对手能够学习使用某个密钥生成的一个或多个明文/密文对。然后,对手的目标是推断使用相同密钥产生的其他密文的基础明文的信息。
-
选择明文攻击(Chosen-plaintext attack):在这种攻击中,对手可以获得如上所述的明文/密文对,用于其选择的明文。
-
选择密文攻击(Chosen-ciphertext attack):攻击者能够额外获得其选择的密文的解密(一些信息),例如,解密攻击者选择的一些密文是否会产生有效的消息。同样,对手的目标是了解使用相同密钥生成的其他密文(对手无法直接获得其解密)的底层明文信息。
密码学的应用领域
密码学的应用领域非常广泛,包括但不限于以下几个方面:
-
数据保护和隐私保护:密码学可以用于保护个人数据、商业数据和政府数据的安全。例如,通过加密算法对敏感数据进行加密,使其只能被授权的用户或组织访问。
-
网络安全:密码学在网络通信和互联网安全中起着重要作用。例如,SSL/TLS协议使用公钥加密算法和数字签名算法来保证网络通信的安全性和完整性。
-
数字货币和区块链:密码学技术支持数字货币(如比特币)的安全交易和账本的可靠性。区块链中的密码学算法确保了交易的匿名性和完整性。
-
身份验证和访问控制:密码学技术可以用于验证用户的身份,确保只有合法用户可以访问系统资源。例如,密码学中的哈希函数和数字签名算法可以用于对用户身份进行验证。
-
数字版权保护:密码学可以用于保护数字内容的版权。数字水印技术使用密码学算法将一些隐藏的标记嵌入到数字内容中,以便识别和追踪盗版。
-
电子投票和选举:密码学也可以用于保证选举和投票的公正性和安全性。通过密码学算法,可以确保选民的投票保密性和选票的完整性。
-
安全协议和身份管理:在复杂的网络环境中,密码学可以用于设计安全协议和身份管理系统,以确保通信和交互的安全性。
总之,密码学是保护信息安全和隐私的关键技术,它在各个领域中都有广泛的应用。
后记
密码学是研究如何保护信息的科学和技术领域。它涵盖了加密、解密、认证、数字签名和密钥管理等方面的内容,旨在确保信息在传输和存储过程中的保密性、完整性和可用性。
在现代社会中,我们的个人和商业信息都需要得到保护,以免受到未经授权的访问和篡改。密码学的应用领域非常广泛,涵盖了各个行业和领域,包括网络通信、电子商务、电子支付、云计算、物联网、数字版权保护等。
密码学的核心在于加密算法。通过使用不同类型的加密算法,可以将原始数据转换为密文,以保护数据的机密性。对称加密算法使用相同的密钥进行加密和解密,速度较快,适合用于大量数据的加密。非对称加密算法使用一对密钥进行加密和解密,安全性更高,适合用于密钥的分发和数字签名。
然而,密码学并不是绝对安全的。随着计算机技术的发展和攻击手段的进步,一些加密算法最终会变得不安全。因此,密码学的研究和发展是一个不断进行的过程。专家们致力于研究新的加密算法、协议和技术,以应对不断变化的安全威胁。
在实际应用中,正确使用密码学也非常重要。强密码的选择、密钥管理和安全协议的设计都是保证密码学有效性的关键因素。此外,用户教育和安全意识的提高也是密码学应用的重要组成部分。
总之,密码学在保护信息安全和隐私方面起着重要的作用。对于个人和企业来说,了解密码学的基本概念和原理,正确使用密码学技术,可以有效地提高信息安全水平,保护重要数据免受未经授权的访问和攻击。
转载自:https://blog.csdn.net/u014727709/article/details/135256474
欢迎 👍点赞✍评论⭐收藏,欢迎指正
相关文章:

浅谈密码学
文章目录 每日一句正能量前言什么是密码学对称加密简述加密语法Kerckhoffs原则常用的加密算法现代密码学的原则威胁模型(按强度增加的顺序) 密码学的应用领域后记 每日一句正能量 人生在世,谁也不能做到让任何人都喜欢,所以没必要…...
Android 混淆是啥玩意儿?
什么是混淆 Android混淆,是伴随着Android系统的流行而产生的一种Android APP保护技术,用于保护APP不被破解和逆向分析。简单的说,就是将原本正常的项目文件,对其类、方法、字段,重新命名a,b,c…之类的字母,…...
【嵌入式——QT】QListWidget
QListWidget类提供了一个基于项的列表小部件,QListWidgetItem是列表中的项,该篇文章中涉及到的功能有添加列表项,插入列表项,删除列表项,清空列表,向上移动列表项,向下移动列表项。 常用API a…...

爬虫入门到精通_基础篇5(PyQuery库_PyQuery说明,初始化,基本CSS选择器,查找元素,遍历,获取信息,DOM操作)
1 PyQuery说明: PyQuery是python中一个强大而又灵活的网页解析库,如果你觉得正则写起来太麻烦,又觉得BeautifulSoup语法太难记,如果你熟悉jQuery的语法那么,PyQuery就是你绝佳的选择。 安装 pip3 install pyquery2 …...

用冒泡排序模拟C语言中的内置快排函数qsort!
目录 编辑 1.回调函数的介绍 2. 回调函数实现转移表 3. 冒泡排序的实现 4. qsort的介绍和使用 5. qsort的模拟实现 6. 完结散花 悟已往之不谏,知来者犹可追 创作不易,宝子们!如果这篇文章对你们有帮助的话,别忘了给个免…...

智慧公厕:打造智慧城市环境卫生新标杆
随着科技的不断发展和城市化进程的加速推进,智慧城市建设已经成为各地政府和企业关注的焦点。而作为智慧城市环境卫生管理的基础设施,智慧公厕的建设和发展也备受重视,被誉为智慧城市的新标杆。本文以智慧公厕源头厂家广州中期科技有限公司&a…...

【学习版】Microsoft Office 2021安装破解教程
本文转载自知乎:https://zhuanlan.zhihu.com/p/655653158 由本人二次整理修改 用到的软件为:Office Tool Plus,下载链接:Office Tool Plus 官方网站 - 一键部署 Office (landian.vip) 下载页面:(随机找个站…...
基于java Springboot实现课程评分系统设计和实现
基于java Springboot实现课程评分系统设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言 文末获取源…...

git操作基本指令
1.查看用户名 git config user.name 2.查看密码 git config user.password 3.查看邮箱 git config user.email 4.修改用户名 git config --global user.name "xxx(新用户名)" 5.修改密码 git config --global user.password "xxx(新密码)" 6.修改…...

YOLO算法
YOLO介绍 YOLO,全称为You Only Look Once: Unified, Real-Time Object Detection,是一种实时目标检测算法。目标检测是计算机视觉领域的一个重要任务,它不仅需要识别图像中的物体类别,还需要确定它们的位置。与分类任务只关注对…...

【Android】更改手机主题导致app数据丢失问题
情景:在使用app过程中更改系统主题(比如从浅色主题改为深色主题),这时activity销毁重建了(即走了onPause、onStop、onSaveInstanceState、onDestroy、onCreate、onRestoreInstanceState、onStart、onResume的生命周期&…...

Dell R730 2U服务器实践3:安装英伟达上代专业AI训练Nvidia P4计算卡
Dell R730是一款非常流行的服务器,2U的机箱可以放入两张显卡,这次先用一张英伟达上代专业级AI训练卡:P4卡做实验,本文记录安装过程。 简洁步骤: 打开机箱将P4显卡插在4号槽位关闭机箱安装驱动 详细步骤: 对…...

Nacos环境搭建 -- 服务注册与发现
为什么需要服务治理 在未引入服务治理模块之前,服务之间的通信是服务间直接发起并调用来实现的。只要知道了对应服务的服务名称、IP地址、端口号,就能够发起服务通信。比如A服务的IP地址为192.168.1.100:9000,B服务直接向该IP地址发起请求就…...

Linux了解
简介 Linux是一种自由和开放源代码的类UNIX操作系统,由芬兰的Linus Torvalds于1991年首次发布。Linux最初是作为支持英特尔x86架构的个人电脑的一个自由操作系统,现在已经被移植到更多的计算机硬件平台,如手机、平板电脑、路由器、视频游戏控…...
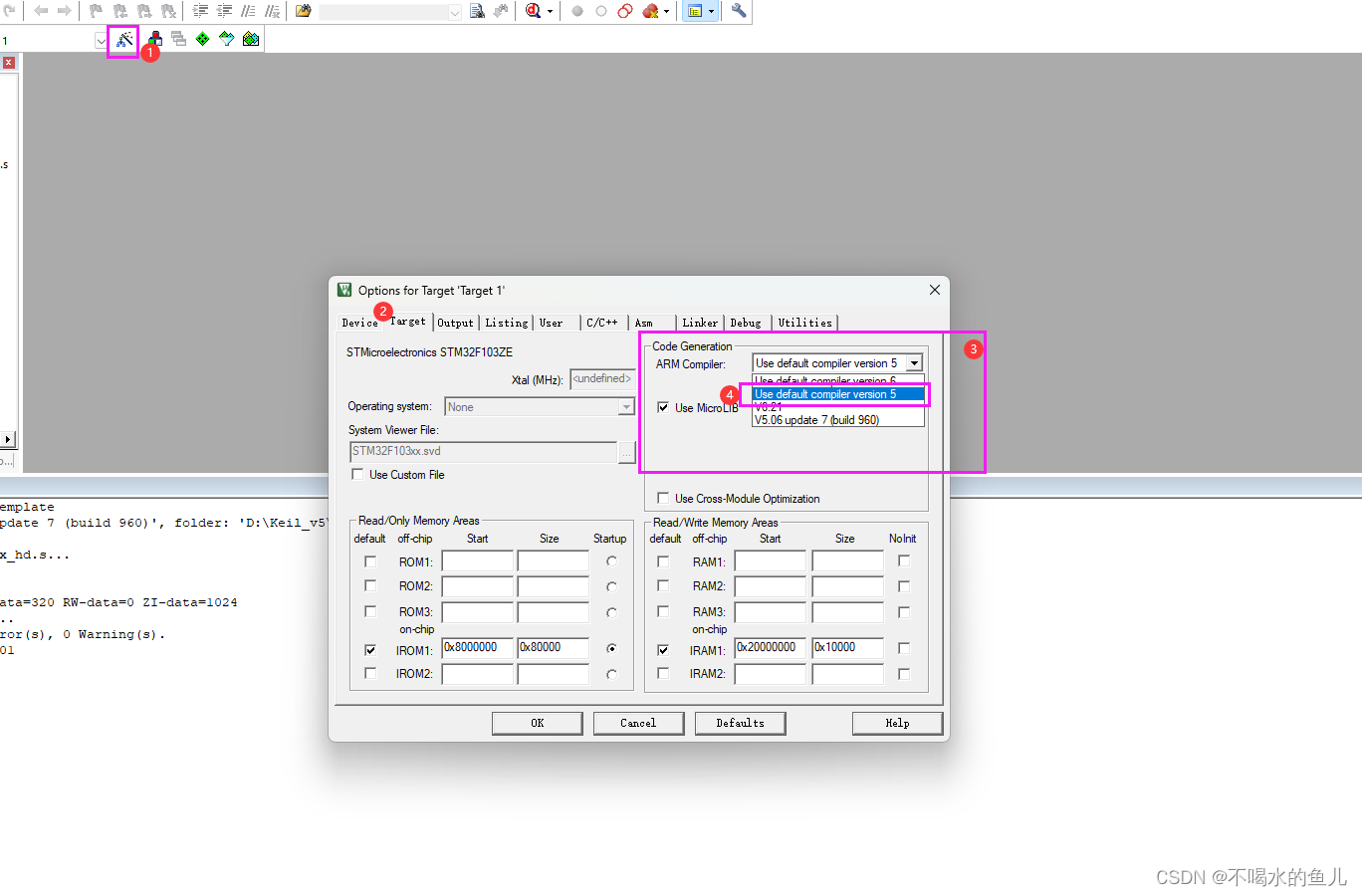
Keil新版本安装编译器ARMCompiler 5.06
0x00 缘起 我手头的项目在使用最新版本的编译器后,烧录后无法正常运行,故安装5.06,测试后发现程序运行正常,以下为编译器的安装步骤。 0x01 解决方法 1. 下载编译器安装文件,可以去ARM官网下载,也可以使用我…...

【基础训练 || Test-1】
总言 主要内容:一些习题。 文章目录 总言一、选择1、for循环、操作符(逗号表达式)2、格式化输出(转换说明符)3、for循环、操作符(逗号表达式、赋值和判等)4、if语句、操作符ÿ…...
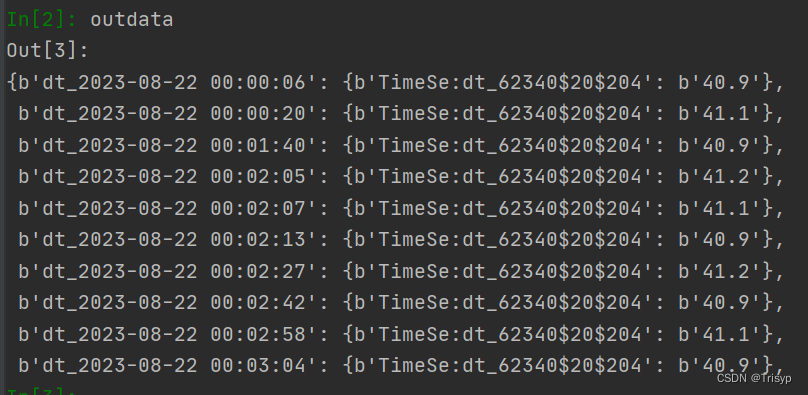
Python读取hbase数据库
1. hbase连接 首先用hbase shell 命令来进入到hbase数据库,然后用list命令来查看hbase下所有表,以其中表“DB_level0”为例,可以看到库名“baotouyiqi”是拼接的,python代码访问时先连接: def hbase_connection(hbase…...

LeetCode41题:缺失的第一个正数(python3)
这道题写的时候完全没有思路,看了很久的题解,才总结出来。 class Solution:def firstMissingPositive(self, nums: List[int]) -> int:nums_set set(nums)n len(nums)for i in range(1, n 1):if i not in nums_set:return ireturn n 1...

C# DataTable 对象操作
实现DataTable按字段进行分类、按列数据汇总、序列化对象数组、所有字段转小写、动态对象数组、数据分页 分类DataTableClassfiy实体: /// <summary>/// 单个分类表/// </summary>public class DataTableClassfiy{/// <summary>/// 分类名称/// &…...

web运行时安全
1.输入验证 对传递的数据的格式、长度、类型(前端和后端都要)进行校验。 对黑白名单校验:比如前端传递了一个用户名,可以搜索该用户是否在白名单或者黑名单列表。 针对黑名单校验,比如: // 手机号验证…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
