Codeforces Round 894 (Div. 3)----->C. Flower City Fence
题目总思路:
要判断是否对称,只需要判断两个放法得到的图形是否相同(竖着放,横着放),这两个放法有个很重要的特性:就是数组中大于1的个数,就是横着放时,第一竖排的高度。那么我们只需要比较两个放法得到的图形,高度是否全部一致。
方法一 :记忆性标记
1.思路:
因为题目输入是一个从大到小的序列,那么假如一个元素大于5那么他也一定大于4,利用这个特性,我们用一个变量 idx记录,上一次遍历到哪里,下一此接着遍历,将个数累加即可。
2.代码:
#include <iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;const int N=2e5+10;int h[N] ;
void Solved(){int n;cin>>n;for(int i=1;i<=n;i++) cin>>h[i];//cnt统计符合条件的元素数量int idx=1, cnt=0;bool flag=true;for(int i=n;i>=1;i--){while(idx<=n&&h[idx]>=i){idx++,cnt++;}if(cnt!=h[i]) {flag=false;break;}}if(flag) cout<<"YES"<<endl;else cout<<"NO"<<endl;}int main()
{int t;cin>>t;while(t--) {Solved();}return 0;
}二 , 方法二 :
1.思路:可以利用差分思想,因为一个程度为 x的木块,他横着放能为这个图形的 [1,n]这个范围,每一个高度增加 1。
2.代码:
#include <iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;const int N=2e5+10;
typedef long long ll;
int h[N] ,temp[N];
void Solved(){memset(temp,0,sizeof temp);int n;cin>>n;for(int i=1;i<=n;i++) cin>>h[i];//注意特判,不然会数组越界。if(h[1]>n){cout<<"NO"<<endl;return;}//差分思想for(int i=1;i<=n;i++){temp[1]++;temp[h[i]+1]--;}//差分数组求前缀和for(int i=1;i<=n;i++) temp[i]+=temp[i-1];bool flag=true;for(int i=1;i<=n;i++){if(temp[i]!=h[i]){flag=false;break;}}if(flag) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}int main()
{int t;cin>>t;while(t--) {Solved();}return 0;
}三,方法三·:二分找大于某个长度的元素数量。
代码:
#include <iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;const int N=2e5+10,M=1e9+10;
typedef long long ll;
int h[N] ,temp[N];
void Solved(){memset(temp,0,sizeof temp);int n;cin>>n;for(int i=1;i<=n;i++) cin>>h[i];bool flag=true;for(int i=n;i>=1;i--){int l=1,r=n;while(l<r){int mid=(l+r+1)>>1;if(h[mid]>=i) l=mid;else r=mid-1;}if(l!=h[i]){flag=false;break;}}if(flag) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}int main()
{int t;cin>>t;while(t--) {Solved();}return 0;
}相关文章:
----->C. Flower City Fence)
Codeforces Round 894 (Div. 3)----->C. Flower City Fence
题目总思路: 要判断是否对称,只需要判断两个放法得到的图形是否相同(竖着放,横着放),这两个放法有个很重要的特性:就是数组中大于1的个数,就是横着放时,第一竖排的高度。…...
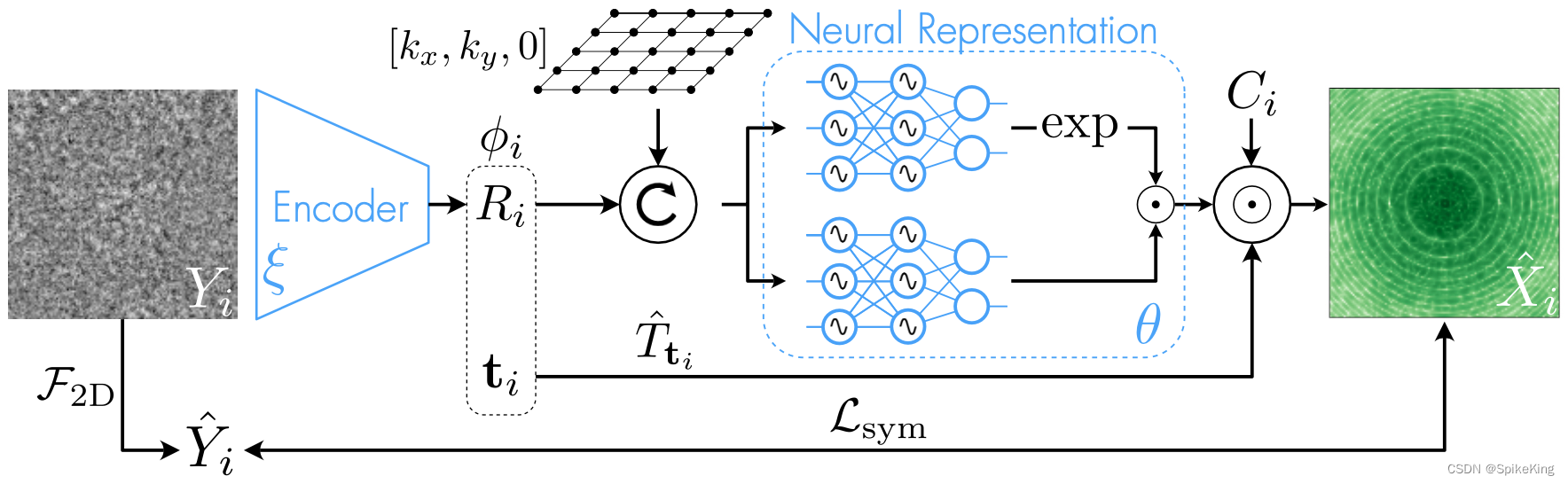
CryoEM - CryoAI: Amortized Inference of Poses 工程源码复现
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/136384544 Paper: CryoAI: Amortized Inference of Poses for Ab Initio Reconstruction of 3D Molecular Volumes from Real Cryo-EM Images CryoAI: 基于摊…...

项目预备知识
导入两个头文件 #include <graphics.h> // 引入 EasyX 的图形库头文件 #include <conio.h> // 引入 conio.h 以使用 getch() 窗口创建函数:小黑屏 initgraph(640, 480, SHOWCONSOLE); closegraph(); //关闭一个窗口 设置背景颜色:这…...
redis实战笔记汇总
文章目录 1 NoSQL入门概述1.1 能干嘛?1.2 传统RDBMS VS NOSQL1.3 NoSQL数据库的四大分类1.4 分布式数据库CAP原理 BASE原则1.5 分布式集群简介1.6 淘宝商品信息的存储方案 2 Redis入门概述2.1 是什么?2.2 能干嘛?2.3 怎么玩?核心…...

elment-ui table表格排序后 清除排序箭头/恢复默认排序 的高亮样式
问题描述: 1.默认排序是按照名称升序排列(图一) 2.在选择了筛选项以及其他排序方式之后,箭头高亮是这样的(图二) 3.当我点击清空按钮后,类型清空了,并且传给后端的排序方式是名称/升…...
)
MySQL数据库基本操作(二)
查询语句 1. 排序查询* 语法:order by 子句* order by 排序字段1 排序方式1 , 排序字段2 排序方式2... * 排序方式:* ASC:升序,默认的。* DESC:降序。 * 注意:* 如果有多个排序条件&#…...
Unity(第十部)时间函数和文件函数
时间函数 using System.Collections; using System.Collections.Generic; using UnityEngine;public class game : MonoBehaviour {// Start is called before the first frame updatefloat timer 0;void Start(){//游戏开始到现在所花的时间Debug.Log(Time.time);//时间缩放值…...

【Java学习笔记】
常见算法 查找算法 1.基本查找 public class BasicSearchDemo01 {public static void main(String[] args) {//基本查找//核心://从0索引开始挨个往后查找//需求:定一个方法利用基本查找,查询某个元素是否存在//数据如下:{131&…...

Python列表生成式你学会了吗
1.最基本的列表生成方式 生成 1-10 之间的整数的一个列表 list1 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] print(list1) # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] list2 list(range(1, 11)) print(list2) # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 2.通过程序的方式生成[4, 9, 16, 25,…...
【Mybatis】快速入门 基本使用 第一期
文章目录 Mybatis是什么?一、快速入门(基于Mybatis3方式)二、MyBatis基本使用2.1 向SQL语句传参2.1.1 mybatis日志输出配置2.1.2 #{}形式2.1.3 ${}形式 2.2 数据输入2.2.1 Mybatis总体机制概括2.2.2 概念说明2.2.3 单个简单类型参数2.2.4 实体…...

在 Rust 中实现 TCP : 1. 联通内核与用户空间的桥梁
内核-用户空间鸿沟 构建自己的 TCP栈是一项极具挑战的任务。通常,当用户空间应用程序需要互联网连接时,它们会调用操作系统内核提供的高级 API。这些 API 帮助应用程序 连接网络创建、发送和接收数据,从而消除了直接处理原始数据包的复杂性。…...
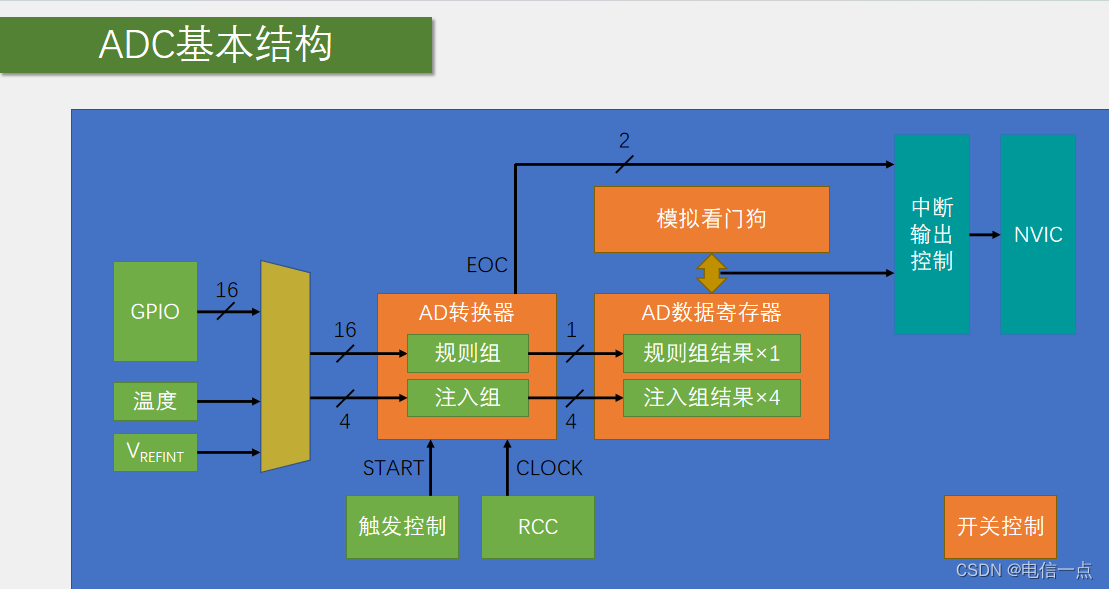
STM32-ADC一步到位学习手册
1.按部就班陈述概念 ADC 是 Analog-to-Digital Converter 的缩写,指的是模拟/数字转换器。它将连续变量的模拟信号转换为离散的数字信号。在 STM32 中,ADC 具有高达 12 位的转换精度,有多达 18 个测量通道,其中 16 个为外部通道&…...

【文件管理】关于上传下载文件的设计
这里主要谈论的是产品设计里面的文件管理,比如文件的上传交互及背后影响到的前后端设计。 上传文件 场景:一条记录,比如个人信息,有姓名,出生年月,性别等一般的字段,还可以允许用户上传附件作为…...

微服务架构 SpringCloud
didi单体应用架构 将项目所有模块(功能)打成jar或者war,然后部署一个进程--医院挂号系统; > 优点: > 1:部署简单:由于是完整的结构体,可以直接部署在一个服务器上即可。 > 2:技术单一:项目不需要复杂的技术栈,往往一套熟…...

前端 css 实现标签的效果
效果如下图 直接上代码: <div class"label-child">NEW</div> // css样式 // 父元素 class .border-radius { position: relative; overflow: hidden; } .label-child { position: absolute; width: 150rpx; height: 27rpx; text-align: cente…...

SLAM基础知识-卡尔曼滤波
前言: 在SLAM系统中,后端优化部分有两大流派。一派是基于马尔科夫性假设的滤波器方法,认为当前时刻的状态只与上一时刻的状态有关。另一派是非线性优化方法,认为当前时刻状态应该结合之前所有时刻的状态一起考虑。 卡尔曼滤波是…...
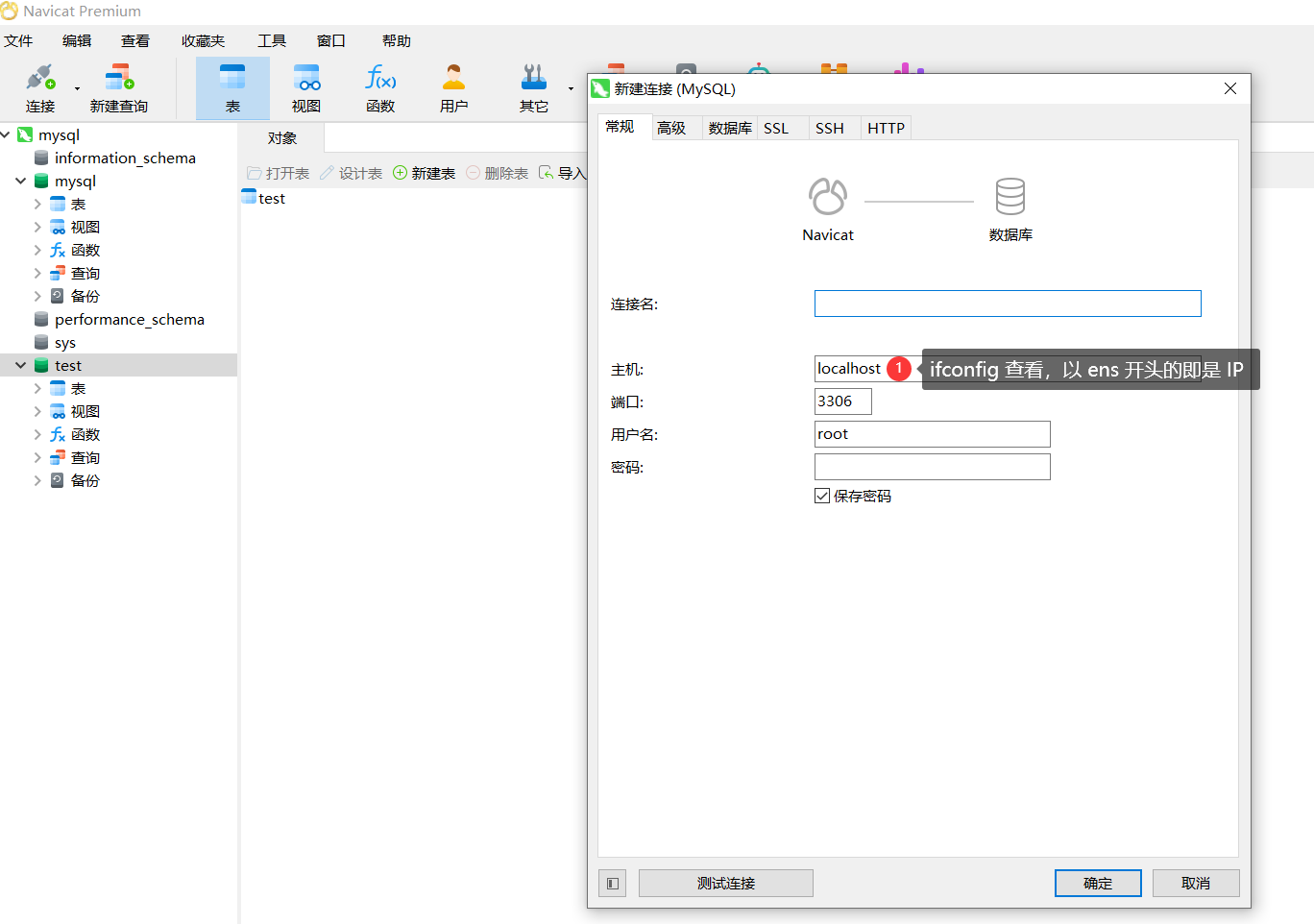
云时代【6】—— 镜像 与 容器
云时代【6】—— 镜像 与 容器 四、Docker(三)镜像 与 容器1. 镜像(1)定义(2)相关指令(3)实战演习镜像容器基本操作离线迁移镜像镜像的压缩与共享 2. 容器(1)…...

【QT+QGIS跨平台编译】之五十三:【QGIS_CORE跨平台编译】—【qgssqlstatementparser.cpp生成】
文章目录 一、Bison二、生成来源三、构建过程一、Bison GNU Bison 是一个通用的解析器生成器,它可以将注释的无上下文语法转换为使用 LALR (1) 解析表的确定性 LR 或广义 LR (GLR) 解析器。Bison 还可以生成 IELR (1) 或规范 LR (1) 解析表。一旦您熟练使用 Bison,您可以使用…...

JMeter性能测试基本过程及示例
jmeter 为性能测试提供了一下特色: jmeter 可以对测试静态资源(例如 js、html 等)以及动态资源(例如 php、jsp、ajax 等等)进行性能测试 jmeter 可以挖掘出系统最大能处理的并发用户数 jmeter 提供了一系列各种形式的…...
你知道什么是回调函数吗?
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
