A Simple Framework for Contrastive Learning of Visual Representations阅读笔记

论文地址:https://arxiv.org/pdf/2002.05709.pdf
目前流行的无监督学范式。通过训练,使模型拥有比较的能力。即,模型能够区别两个数据(instance)是否是相同的。这在 深度聚类 领域受到广泛的关注。(在有监督中的 few-shot, 使用一些类让模型学会比较,再用一些新类去测试模型的比较能力)
我们分几个模块了解对比学习。
数据增强
对比学习主要是通过拉进 正例对 之间特征表示的相似度;以及拉远 负例对 之间特征表示的相似度。
从而使模型具有 对比的能力。因为是无监督学习,我们的数据没有标签。我们构建正例对的方法就是通过数据增强(基本不改变数据的语义信息)。
数据增强的方法有很多种:
图片数据增强
文本数据增强
语音数据增强
图数据增强
正负例对的构建
原数据:(x1,x2,x3)(x_1, x_2, x_3)(x1,x2,x3);
增强数据a:(x1a,x2a,x3a)(x_1^a, x_2^a, x_3^a)(x1a,x2a,x3a);
增强数据b:(x1b,x2b,x3b)(x_1^b, x_2^b, x_3^b)(x1b,x2b,x3b);
| Aug_data{a & b} | x1bx_1^bx1b | x2bx_2^bx2b | x3bx_3^bx3b |
|---|---|---|---|
| x1ax_1^ax1a | (x1a,x1b)\color{red}(x_1^a, x_1^b)(x1a,x1b) | (x1a,x2b)(x_1^a, x_2^b)(x1a,x2b) | (x1a,x3b)(x_1^a, x_3^b)(x1a,x3b) |
| x2ax_2^ax2a | (x2a,x1b)(x_2^a, x_1^b)(x2a,x1b) | (x2a,x2b)\color{red}(x_2^a, x_2^b)(x2a,x2b) | (x2a,x3b)(x_2^a, x_3^b)(x2a,x3b) |
| x3ax_3^ax3a | (x3a,x1b)(x_3^a, x_1^b)(x3a,x1b) | (x3a,x2b)(x_3^a, x_2^b)(x3a,x2b) | (x3a,x3b)\color{red}(x_3^a, x_3^b)(x3a,x3b) |
构成的正例对:红色;
构成的负例对:黑色。
上面说的只是原始的 对比对的构造方式。 现在还有根据 语义信息 进行去除假负例对。
假负例对: x1,x2x_1, x_2x1,x2 属于一个 簇类,(x1a,x2b)(x_1^a, x_2^b)(x1a,x2b) 却属于负例对,实际上应该属于正例对,且他们的特征表示的相似度应该很大。
编码器 Φ(⋅)\Phi(\cdot)Φ(⋅)
将图片,文本,语音,图等进行编码。得到特征矩阵 HHH。
对于一个原数据: X={xi}i=0MX = \{ x_i \}_{i=0}^MX={xi}i=0M, 我们得到其相应的增数据:Xa={xia}i=0MX^a = \{ x_i^a \}_{i=0}^MXa={xia}i=0M, Xb={xib}i=0MX^b = \{ x_i^b \}_{i=0}^MXb={xib}i=0M。MMM是batch size的大小。
然后经过编码得到特征矩阵:Ha=Φ(Xa),Hb=Φ(Xb)H^a = \Phi(X^a), H^b = \Phi(X^b)Ha=Φ(Xa),Hb=Φ(Xb),其中,Ha,Hb∈RM×hidden_sizeH^a, H^b \in \mathbb{R}^{M \times hidden\_size}Ha,Hb∈RM×hidden_size。
Project head f(⋅)f(\cdot)f(⋅)
一般使用一个两层的线性MLP或者三层的非线性MLP。将得到的Feature Matrix映射到一个字空间(subspace)。一般都是将其映射为128维。
对于得到的特征矩阵:Ha,HbH^a, H^bHa,Hb。我们经过 f(⋅)f(\cdot)f(⋅) 得到映射的子空间: Za=f(Ha),Zb=f(Hb)Z^a = f(H^a), Z^b = f(H^b)Za=f(Ha),Zb=f(Hb), 其中,Za,Zb∈RM×128Z^a, Z^b \in \mathbb{R}^{M \times 128}Za,Zb∈RM×128。
最小化对比损失
得到子空间表示后,在使用对比损失函数,最小化损失函数。
lia=−logexp(s(zia,zib)/τ)∑j=1M[exp(s(zia,zja)/τ)+exp(s(zia,zjb)/τ)]lib=−logexp(s(zib,zia)/τ)∑j=1M[exp(s(zib,zja)/τ)+exp(s(zib,zjb)/τ)]L=12M∑i=1M(lia+lib)\mathcal{l}^a_i = -\log \frac{\exp(s(z_i^a, z_i^b)/\tau)}{\sum_{j=1}^{M} [\exp(s(z_i^a, z_j^a)/\tau) + \exp(s(z_i^a, z_j^b)/\tau) ]} \\ \mathcal{l}^b_i = -\log \frac{\exp(s(z_i^b, z_i^a)/\tau)}{\sum_{j=1}^{M} [\exp(s(z_i^b, z_j^a)/\tau) + \exp(s(z_i^b, z_j^b)/\tau) ]} \\ \mathcal{L} = \frac{1}{2M} \sum_{i=1}^{M} (\mathcal{l}^a_i + \mathcal{l}^b_i) lia=−log∑j=1M[exp(s(zia,zja)/τ)+exp(s(zia,zjb)/τ)]exp(s(zia,zib)/τ)lib=−log∑j=1M[exp(s(zib,zja)/τ)+exp(s(zib,zjb)/τ)]exp(s(zib,zia)/τ)L=2M1i=1∑M(lia+lib)
其中,τ\tauτ 是温度参数,MMM 是batch size的大小,s(⋅)s(\cdot)s(⋅) 是相似性度量,具体表达为:s(zi,zj)=ziTzj/∣∣zi∣∣2⋅∣∣zj∣∣2s(z_i, z_j) = z_i^Tz_j / ||z_i||_2 \cdot ||z_j||_2s(zi,zj)=ziTzj/∣∣zi∣∣2⋅∣∣zj∣∣2。
实验的超参数和一些细节
相关文章:

A Simple Framework for Contrastive Learning of Visual Representations阅读笔记
论文地址:https://arxiv.org/pdf/2002.05709.pdf 目前流行的无监督学范式。通过训练,使模型拥有比较的能力。即,模型能够区别两个数据(instance)是否是相同的。这在 深度聚类 领域受到广泛的关注。(在有监…...
mac安装开发工具:clipy、iterm2、go、brew、mysql、redis、wget等
wget brew install wget clipy Releases Clipy/Clipy GitHub 环境变量 ~下有三个文件 .zshrc .zprofile .bash_profile > cat .zshrc export PATH$PATH:/usr/local/mysql/bin> cat .zprofile eval "$(/opt/homebrew/bin/brew shellenv)"> cat .bas…...
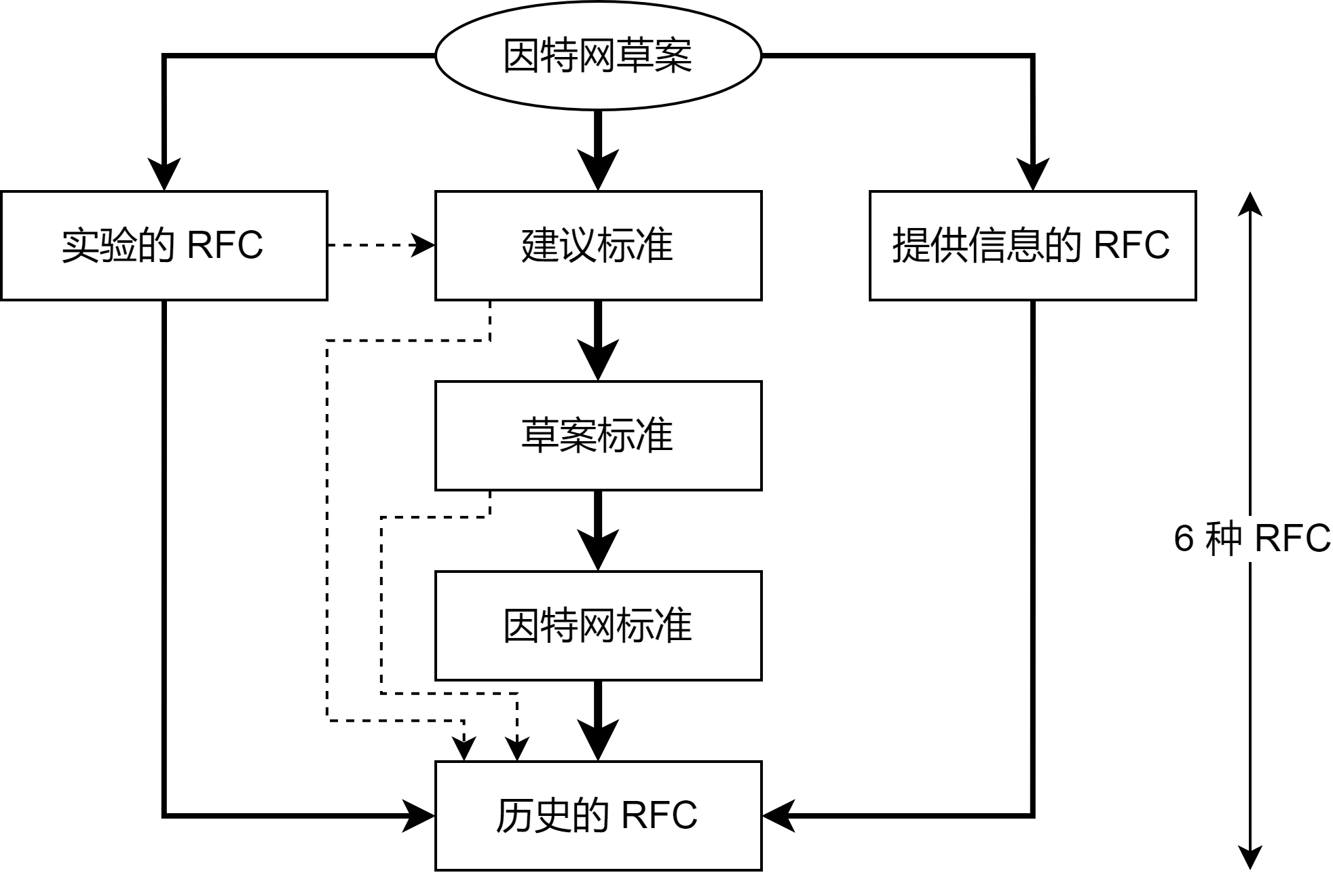
DJ1-1 计算机网络和因特网
目录 一、计算机网络 二、Interent 1. Internet 的介绍 2. Internet 的具体构成 3. Internet 提供的服务 4. Internet 的通信控制 一、计算机网络 定义:是指两台以上具有独立操作系统的计算机通过某些介质连接成的相互共享软硬件资源的集合体。 计算机网络向…...
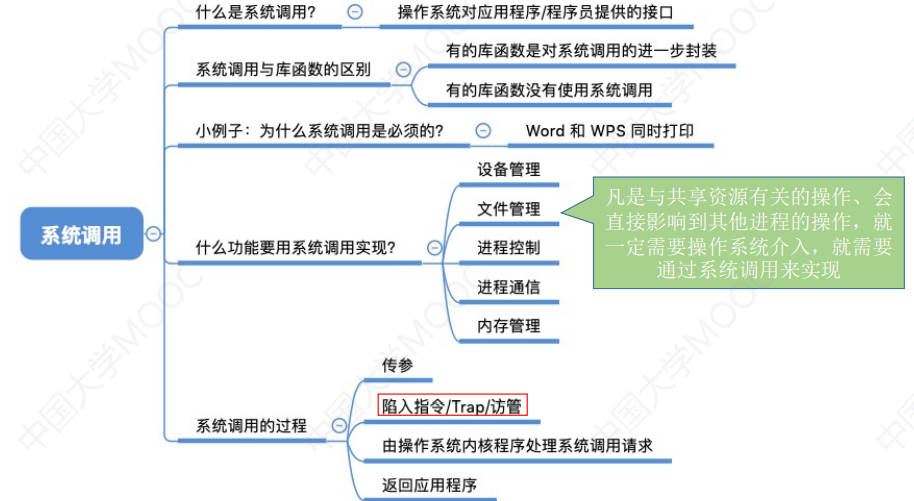
[1.3.3]计算机系统概述——系统调用
文章目录第一章 计算机系统概述系统调用(一)什么是系统调用,有何作用(二)系统调用与库函数的区别(三)小例子:为什么系统调用是必须的(四)什么功能要用到系统调…...

【Java开发】JUC进阶 03:读写锁、阻塞队列、同步队列
1 读写锁(ReadWriteLock)📌 要点实现类:ReentrantReadWirteLock通过读写锁实现更细粒度的控制,当然通过Synchronized和Lock锁也能达到目的,不过他们会在写入和读取操作都给加锁,影响性能&#x…...

Fragment中获取Activity的一点点建议
平时的Android开发中,我们经常要在Fragment中去获取当前的Activity实例,刚开始的时候可能使用使用Fragment提供的getActivity方法来获取,但是这个方法可能返回null,为了让程序可以正常运行,项目中就出现大量下面这样的…...

Java Math类
Java Math 类是 Java 标准库中提供的一个数学计算类,它提供了很多数学函数,如三角函数、指数函数、对数函数等。在实际工作中,Java Math 类常常被用于处理数学计算问题,例如计算复杂的数学公式、实现数学算法等。本文将详细介绍 J…...

Javascript -- 加载时间线 正则表达式
js加载时间线 1、创建Document对象,开始解析web页面,解析html元素和他们的文本内容后添加Element对象和Text节点到文档中。这个阶段的document.readyState ‘loading’ 2、遇到link外部css,创建线程加载,并继续解析文档 3、遇到…...
gdb/git的基本使用
热爱编程的你,一定经常徘徊在写bug和改bug之间,调试器也一定是你随影而行的伙伴,离开了它你应该会寝食难安吧! 目录 gdb的使用 断点操作 运行调试 观察数据 Git的使用 仓库的创建和拉取 .gitignore “三板斧” 常用指令 gd…...

信息安全与数学基础-笔记-④二次同余方程
知识目录二次同余方程的解欧拉判别式Legendre (勒让德符号)二次同余方程的解 什么是二次同余方程的解 注意这里二次同余方程和一次同余方程是不一样的 在x2x^2x2 三 a (mod m) 方程中举例 ↓ 解即剩余类,因为是模m,所以我们在 [ 0, m-1 ]中逐个代入看是…...

Luogu P4447 [AHOI2018初中组]分组
题目链接:传送门 将nnn个可重复的整数分为mmm组,每组中的数必须连续且不重复,使人数最少的组人数最多。 两个最值肯定第一想到二分,每次二分出一个值,判断在这个值为答案的前提下能否完成分组。 在思考判别函数时发现…...
手把手创建flask项目
Flask 框架流程 什么是Flask: Flask诞生于2010年, 使用python语言基于Werkzeug工具箱编写的轻量级Web开发框架 Flask本身相当于一个内核, 其他几乎所有的功能都要用到扩展(邮件:Flask-Mail, 用户认证:Flask-Login, 数据库:Flask-SQLAlchemy). Flask的核心在于Werkz…...

SpringCloud-4_Eureka服务注册与发现
Eureka作为一个老牌经典的服务注册&发现技术,其设计和理念,也在影响后面的组件。目前主流的服务注册&发现的组件是Nacos当前项目架构问题分析-引出Eureka问题分析:1.在企业级项目中,服务消费访问请求会存在高并发2.如果只…...

【react全家桶】生命周期
文章目录04 【生命周期】1.简介2.初始化阶段2.1 constructor2.2 componentWillMount(即将废弃)2.3 static getDerivedStateFromProps(新钩子)2.4 render2.5 componentDidMount2.6 初始化阶段总结3.更新阶段3.1 componentWillRecei…...
虚拟机安装Windows 10
虚拟机安装Windows 10 镜像下载 方法一:下载我制作好的镜像文件->百度网盘链接 提取码:Chen 方法二:自己做一个 进入微软官网链接 下载"MediaCreationTool20H2" 运行该工具 点击下一步选择路径,等他下载好就欧克了…...

【CMU15-445数据库】bustub Project #2:B+ Tree(下)
Project 2 最后一篇,讲解 B 树并发控制的实现。说实话一开始博主以为这块内容不会很难(毕竟有 Project 1 一把大锁摆烂秒过的历史x),但实现起来才发现不用一把大锁真的极其痛苦,折腾了一周多才弄完。 本文分基础版算法…...

leetcode 困难 —— 外星文字典(拓扑排序)
题目: 现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。 给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。 请你根据该词典还原出此语言中已知的字…...
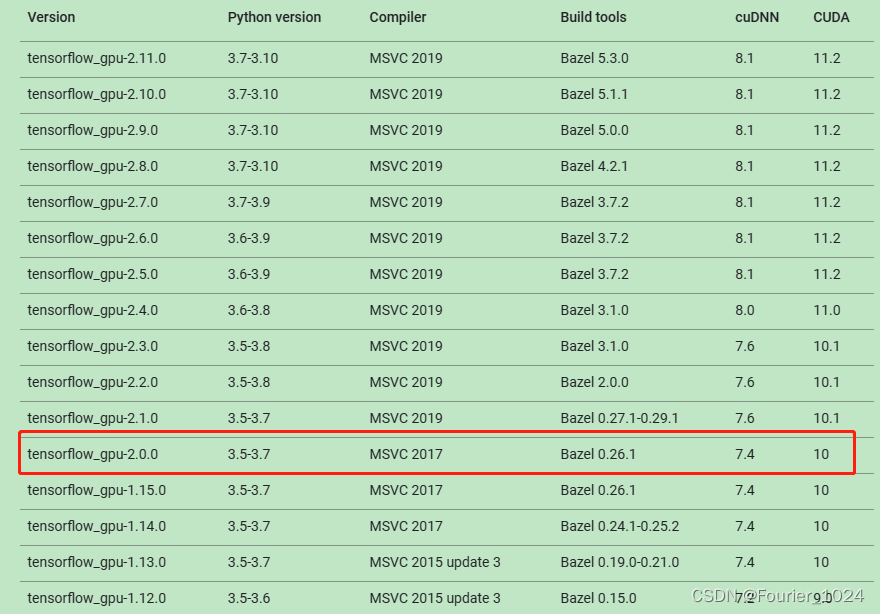
ubuntu server 18.04使用tensorflow进行ddqn训练全过程
0. 前言 需要使用ddqn完成某项任务,为了快速训练,使用带有GPU的服务器进行训练。记录下整个过程,以及遇到的坑。 1. 选择模板代码 参考代码来源 GitHub 该代码最后一次更新是Mar 24, 2020。 环境配置: python3.8 运行安装脚本…...

2023年全国最新二级建造师精选真题及答案14
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 二、多选题 61.已经取得下列资质的设计单位,可以直接申请相应类别施工总承包一级…...
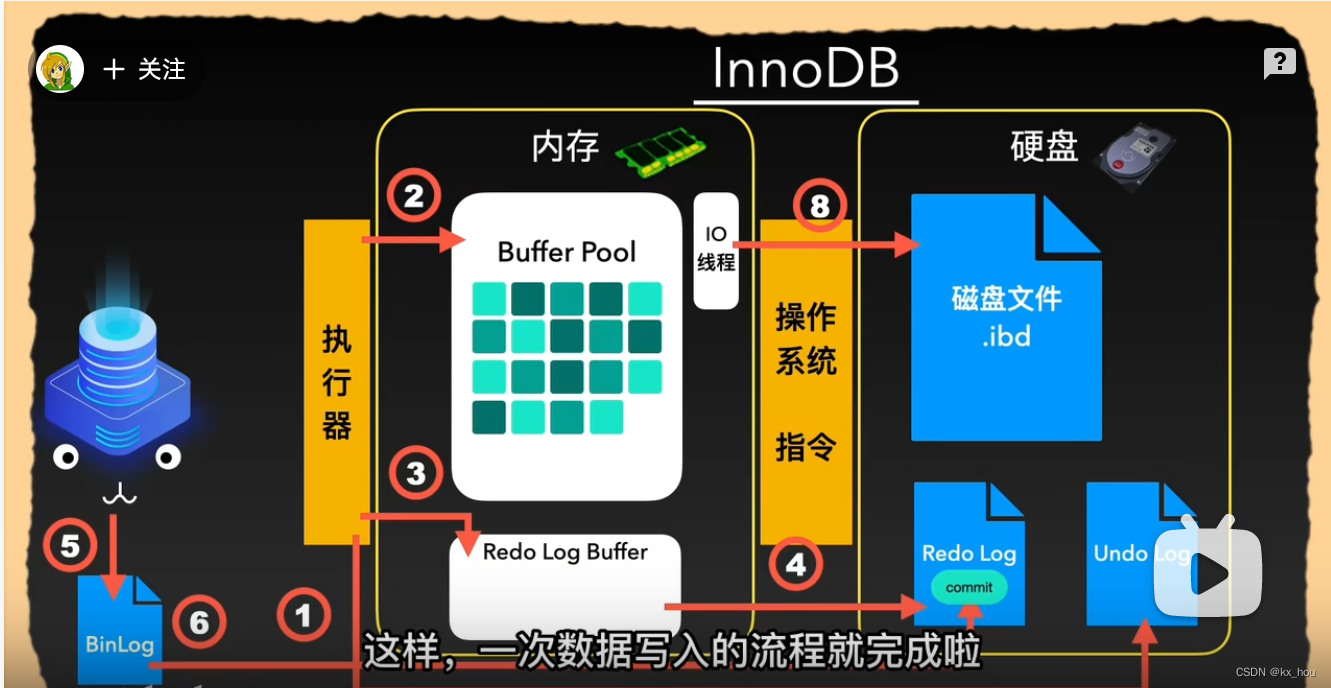
mysql一条语句的写入原理
mysql写入原理 我们知道在mysql数据库最核心的大脑就是执行引擎; 其中的默认引擎Innodb在可靠执行和性能中做出来平衡; innodb支持在事务控制、读写效率,多用户并发,索引搜索方面都表现不俗; innodb如何进行数据写入…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
