【C++ AVL树】
文章目录
- AVL树
- AVL树的概念
- AVL树节点的定义
- AVL树的插入
- AVL树的旋转
- 右单旋
- 左单旋
- 左右双旋
- 右左双旋
- 代码实现
- 总结
AVL树
AVL树的概念
二叉搜索树在顺序有序或接近有序的情况下,而插入搜索树将退化为单叉树,此时查找的时间复杂度为O(n),效率低下。
两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新节点后,保证每个节点的左右子树高度差的绝对值不超过1,即可降低树的高度,减少平均搜索长度。因此,AVL树也被叫做高度平衡二叉搜索树,插入,查找,删除在平均和最坏情况下的时间复杂度都是O( l o g 2 n log_2 n log2n)。
AVL树节点的定义
template<class K, class V>struct AVLTreeNode{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _bf; //balance factor 平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}};
注意:实现AVL树平衡因子不是必须的,只不过有了平衡因子帮助我们更便捷地控制整棵树。
AVL树的插入
- 根据二叉搜索树的规则插入新节点
bool Insert(const pair<K, V> & kv){root为空,特殊处理if (_root == nullptr){_root = new Node(kv);return true;}Node* curr = _root;Node* parent = nullptr;while (curr){if (curr->_kv.first < kv.first){parent = curr;curr = curr->_right;}else if (curr->_kv.first > kv.first){parent = curr;curr = curr->_left;}else{return false;}}将新节点和其父亲节点链接起来Node* newnode = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = newnode;elseparent->_left = newnode;newnode->_parent = parent;......}
- 不断向上更新平衡因子
- 当前平衡因子为0,说明插入之前平衡因子为1 / -1,插入之后不改变树的高度,不会影响其他祖先节点,此时更新结束。
- 当前平衡因子为1 / -1,说明插入之前平衡因子为0,插入之后当前节点地高度发生变化,会影响其他祖先节点,但是不违反规则,需要向上对祖先节点进行更新,直至当前节点为root。
- 当前平衡因子为 2 / -2,此时当前节点所在地子树违反了平衡规则,需要进行处理–>旋转。
while (parent)
{if (parent->_left == newnode){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){newnode = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){旋转处理}else{assert(false);}
}
AVL树的旋转
右单旋
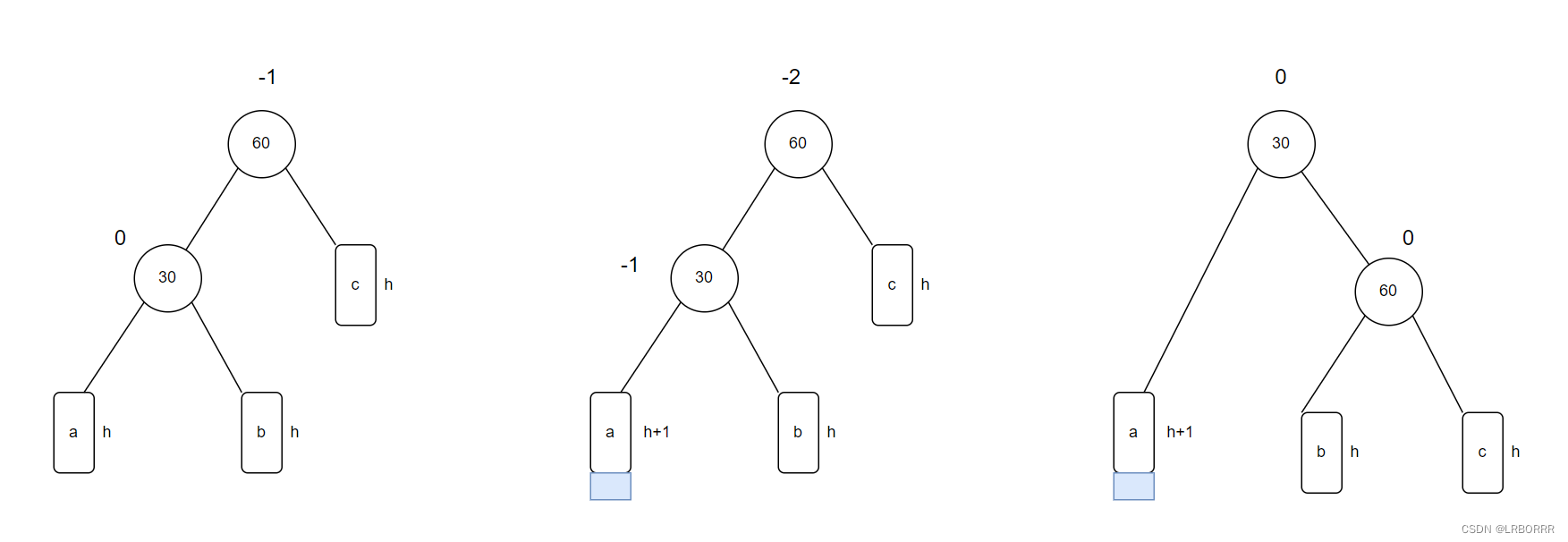
void RotatoR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subL;elseppnode->_right = subL;subL->_parent = ppnode;}parent->_bf = 0;subL->_bf = 0;
}
左单旋
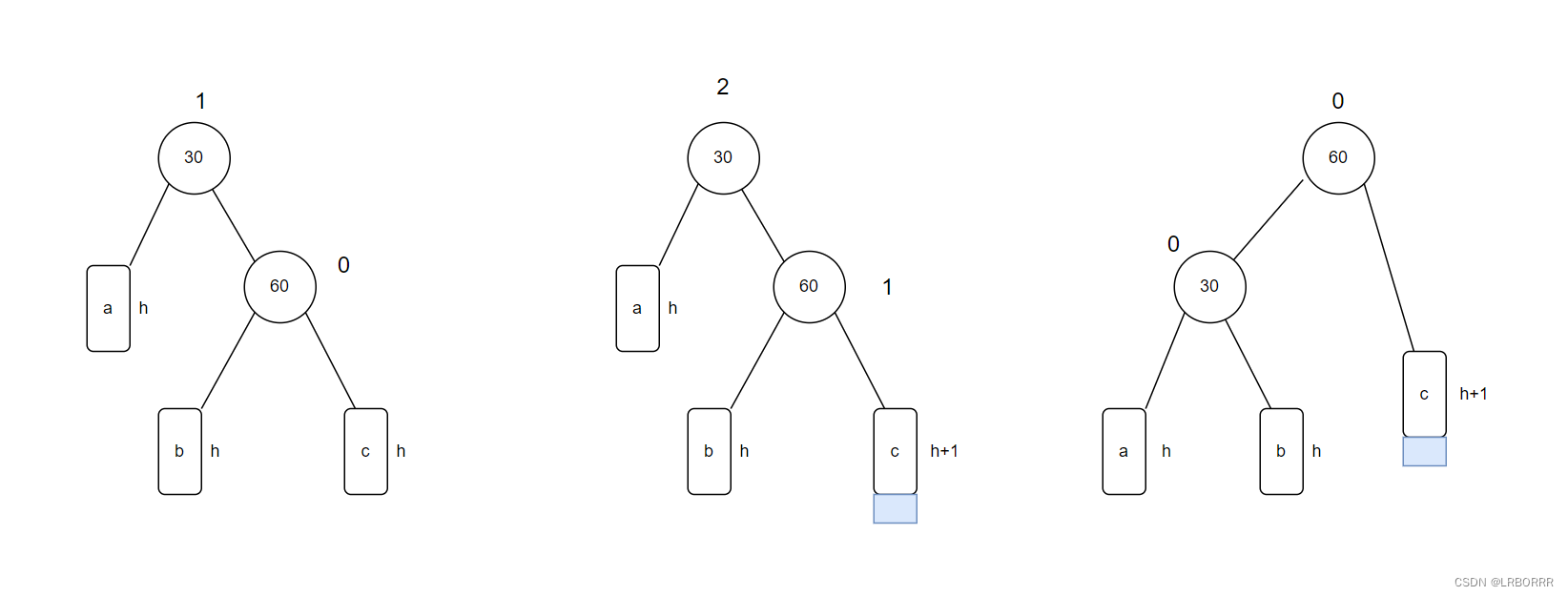
void RotatoL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subR;elseppnode->_right = subR;subR->_parent = ppnode;}parent->_bf = 0;subR->_bf = 0;
}
左右双旋
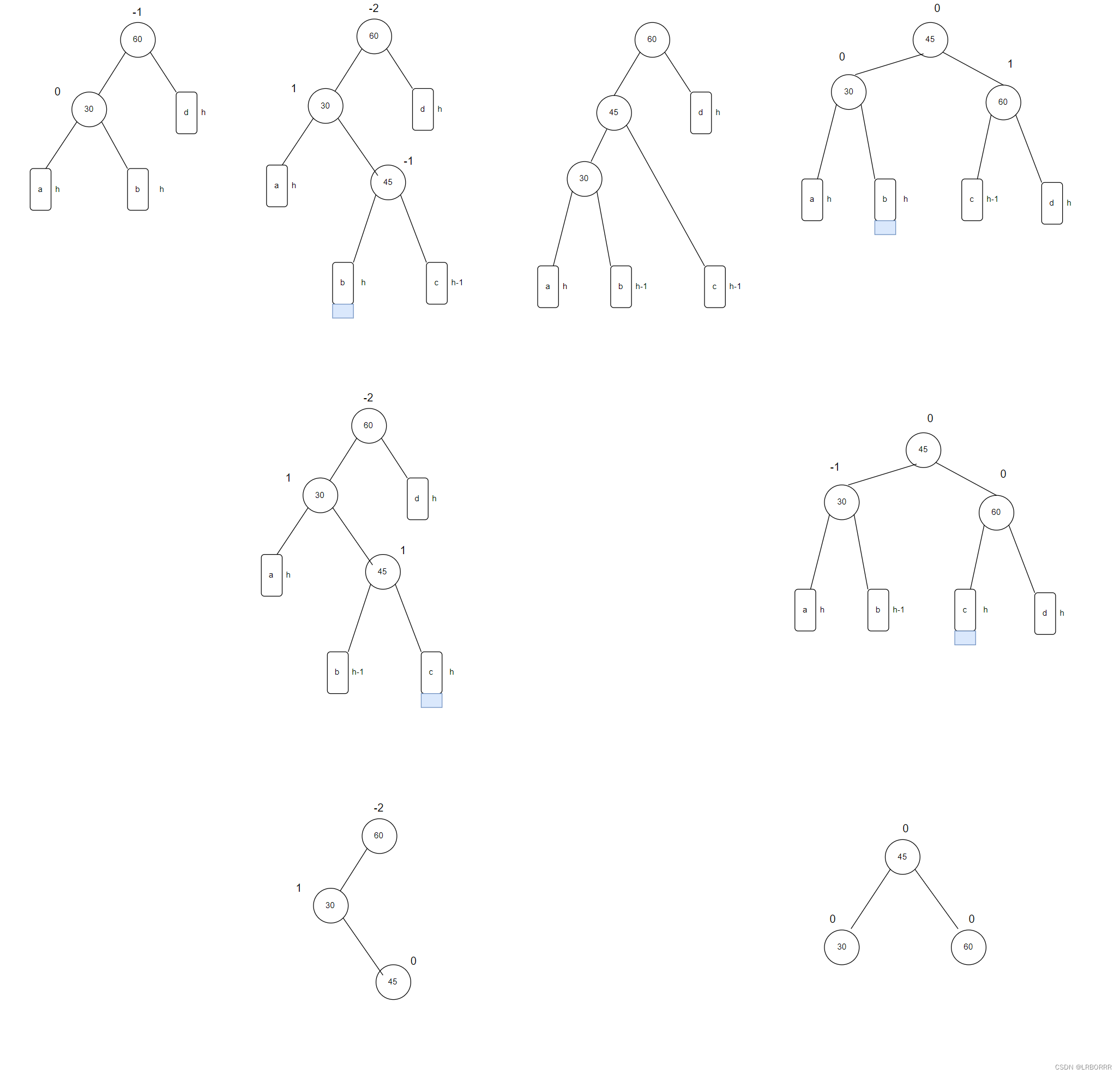
旋转之前,45的平衡因子可能是-1/0/1,旋转完成之后,根据情况对其他节点的平衡因子进行调整
void RotatoLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotatoL(subL);RotatoR(parent);subLR->_bf = 0;if (bf == 0){subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;parent->_bf = 1;}
}
右左双旋
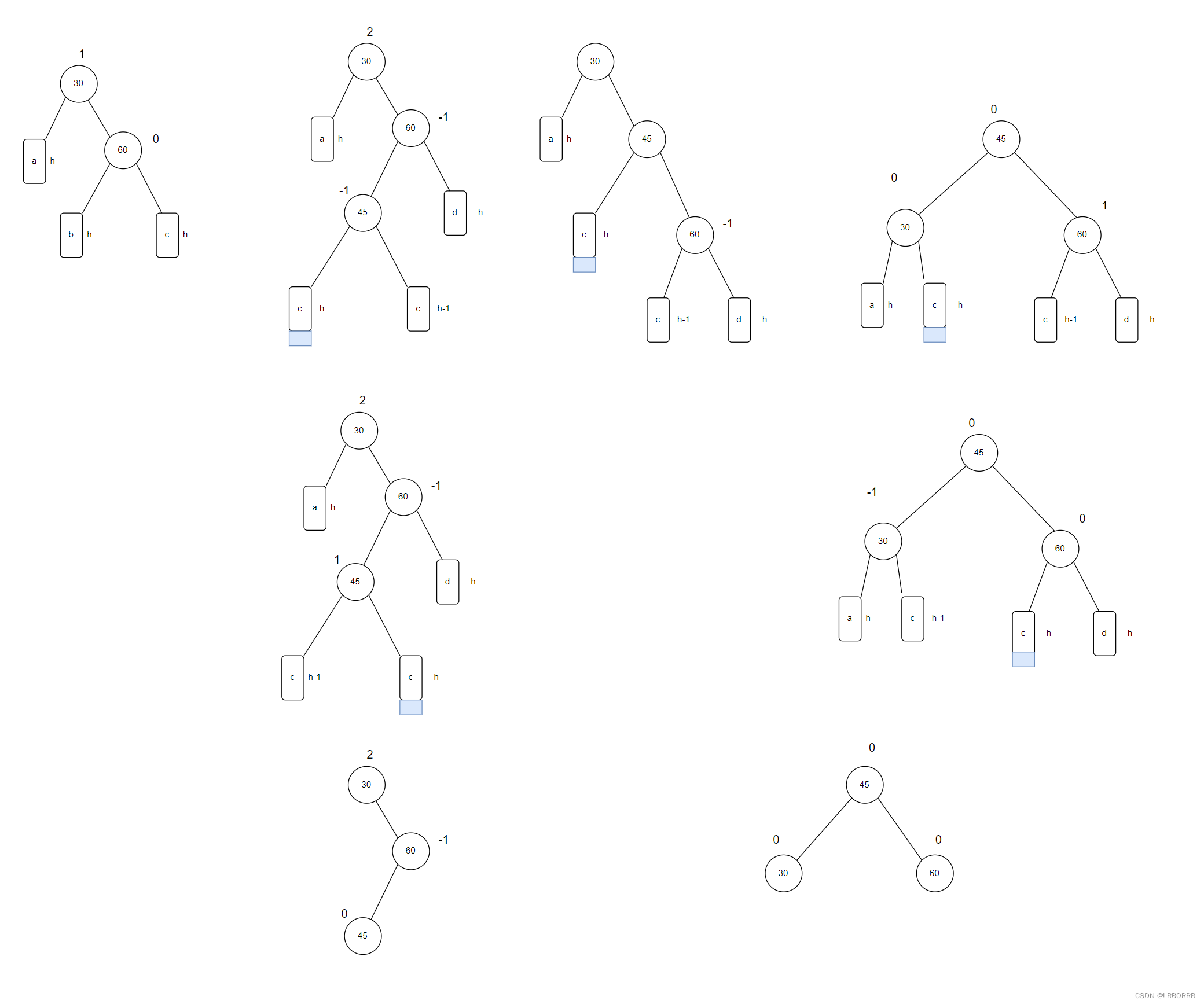
void RotatoRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;subRL->_bf = 0;RotatoR(subR);RotatoL(parent);if (bf == 0){subR->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;}
}
代码实现
namespace xxx
{template<class K, class V>struct AVLTreeNode{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _bf; //balance factor 平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}};template<class K, class V>class AVLTree{typedef AVLTreeNode<K, V> Node;public:bool Insert(const pair<K, V> & kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* curr = _root;Node* parent = nullptr;while (curr){if (curr->_kv.first < kv.first){parent = curr;curr = curr->_right;}else if (curr->_kv.first > kv.first){parent = curr;curr = curr->_left;}else{return false;}}Node* newnode = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = newnode;elseparent->_left = newnode;newnode->_parent = parent;while (parent){if (parent->_left == newnode){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){newnode = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){if (parent->_bf == 2 && newnode->_bf == 1){RotatoL(parent);}else if (parent->_bf == -2 && newnode->_bf == -1){RotatoR(parent);}else if (parent->_bf == -2 && newnode->_bf == 1){RotatoLR(parent);}else if (parent->_bf == 2 && newnode->_bf == -1){RotatoRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}void RotatoL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subR;elseppnode->_right = subR;subR->_parent = ppnode;}parent->_bf = 0;subR->_bf = 0;}void RotatoR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subL;elseppnode->_right = subL;subL->_parent = ppnode;}parent->_bf = 0;subL->_bf = 0;}void RotatoLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotatoL(subL);RotatoR(parent);subLR->_bf = 0;if (bf == 0){subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;parent->_bf = 1;}}void RotatoRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;subRL->_bf = 0;RotatoR(subR);RotatoL(parent);if (bf == 0){subR->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;}}void InOrder(){_InOrder(_root);cout << endl;}bool IsAVLTree(){return _IsAVLTree(_root);}private:bool _IsAVLTree(Node* root){if (root == nullptr)return true;int leftH = Height(root->_left);int rightH = Height(root->_right);return abs(leftH - rightH) <= 1&& _IsAVLTree(root->_left)&& _IsAVLTree(root->_right);}int Height(Node* node){if (node == nullptr)return 0;int leftH = Height(node->_left);int rightH = Height(node->_right);return 1 + max(leftH, rightH);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.second << ' ';_InOrder(root->_right);}Node* _root = nullptr;};
}
总结
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 l o g 2 ( N ) log_2 (N) log2(N)。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

【C++ AVL树】
文章目录 AVL树AVL树的概念AVL树节点的定义AVL树的插入AVL树的旋转右单旋左单旋左右双旋右左双旋 代码实现 总结 AVL树 AVL树的概念 二叉搜索树在顺序有序或接近有序的情况下,而插入搜索树将退化为单叉树,此时查找的时间复杂度为O(n),效率低…...

记录一次架构优化处理性能从3千->3万
0.背景 优化Kafka消费入Es,适配600台设备上报数据,吞吐量到达2万每秒 1.环境配置 2.压测工具 3.未优化之前的消费逻辑 4.优化之后的消费流程 5.多线程多ESclient 6.修改ES配置,增加kafka分区,增加线程,提升吞吐量 7.…...

c++二进制位运算使用方法
文章主要内容: C 中的位运算符主要用于对整数类型的数据进行位操作,包括按位与(&)、按位或(|)、按位异或(^)、取反(~)、左移(<<&#…...

TypeScript之JSON点语法调用
场景 当我们想要通过将JSON中的属性名赋值给一个变量,并且通过点语法实现字段调用.常规的String变量保存会出现下述问题,就可以通过String[][]实现动态调用字段. let parentJSON{"name":"liupeng"}let a:String;Object.keys(parentJSON).forEach(key >…...

手撕Java集合之简易版Deque(LinkedList)
在目前,许多互联网公司的面试已经要求能手撕集合源码,集合源码本身算是源码里比较简单的一部分,但是要在面试极短的10来分钟内快速写出一个简易版的源码还是比较麻烦的,很容易出现各种小问题。所以在平时就要注重这方面的联系。 以…...
)
MySQL知识点归纳总结(二)
10、MVCC实现原理? 事务ID(Transaction ID):每个事务在执行时都会被分配一个唯一的事务ID,用于标识该事务的开始时间顺序。事务ID是一个递增的整数,随着每个新事务的开始而递增。 Undo日志(Un…...

vue:实现顶部消息横向滚动通知
前言 系统顶部展示一个横向滚动的消息通知,就是消息内容从右往左一直滚动。 效果如下: 代码 使用 <template><div class"notic-bar"><img :src"notic" class"notice-img" /><div class"noti…...

[笔记] wsl 禁用配置 win系统环境变量+代理
wsl 配置禁用 win系统环境变量 进入 wsl 的 /etc/wsl.conf 目录,增加以下配置: [interop] enabledfalse appendWindowsPathfalse然后退出wsl,并且执行关闭正在运行的 wsl,执行命令 wsl --shutdown 最后重新进入wsl 即可。 参考…...
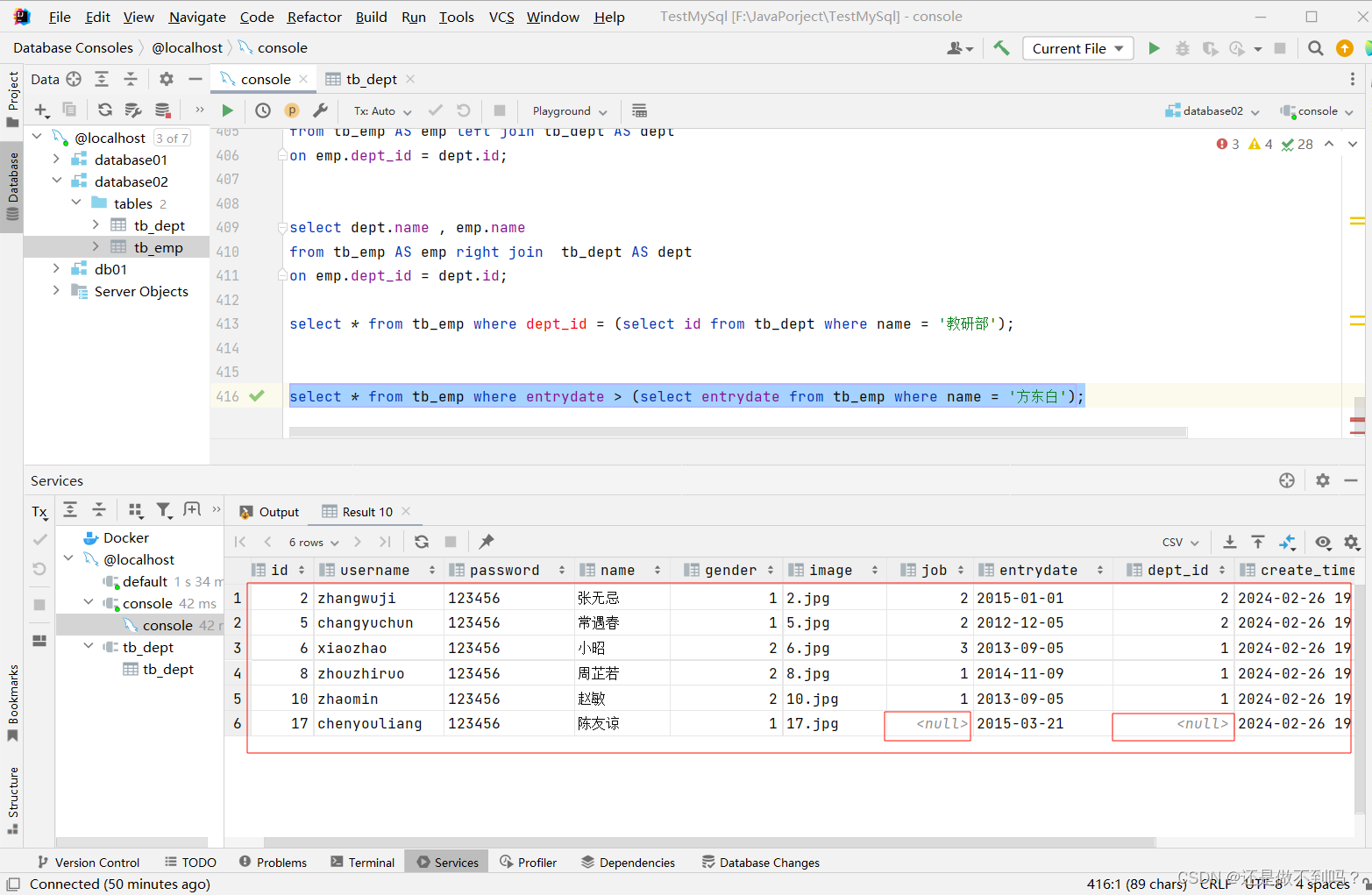
Mysql标量子查询
目录 子查询标量子查询数据准备 子查询 SQL语句中嵌套select语句,称为嵌套查询,又称子查询。 SELECT * FROM t1 WHERE column1 ( SELECT column1 FROM t2 ... );子查询外部的语句可以是insert / update / delete / select 的任何一个&…...
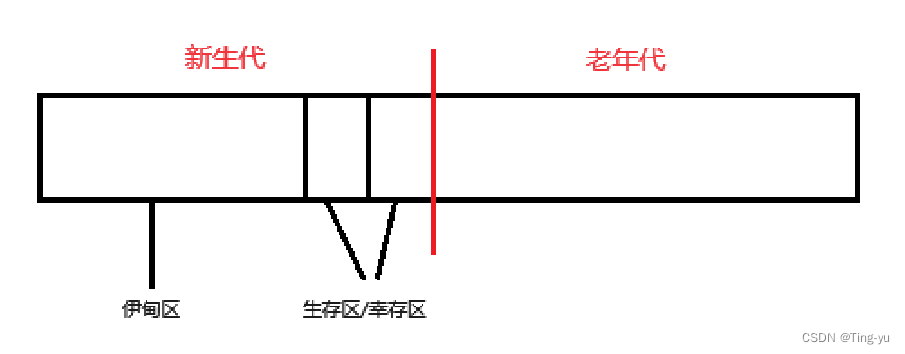
深入了解Java虚拟机(JVM)
Java虚拟机(JVM)是Java程序运行的核心组件,它负责解释执行Java字节码,并在各种平台上执行。JVM的设计使得Java具有跨平台性,开发人员只需编写一次代码,就可以在任何支持Java的系统上运行。我们刚开始学习Ja…...
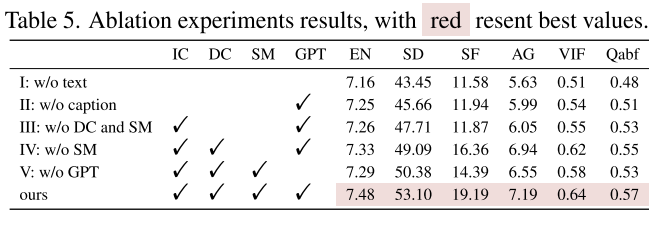
Image Fusion via Vision-Language Model【文献阅读】
阅读目录 文献阅读AbstractIntroduction3. Method3.1. Problem Overview3.2. Fusion via Vision-Language Model 4. Vision-Language Fusion Datasets5. Experiment5.1Infrared and Visible Image Fusion 6. Conclusion个人总结 文献阅读 原文下载:https://arxiv.or…...
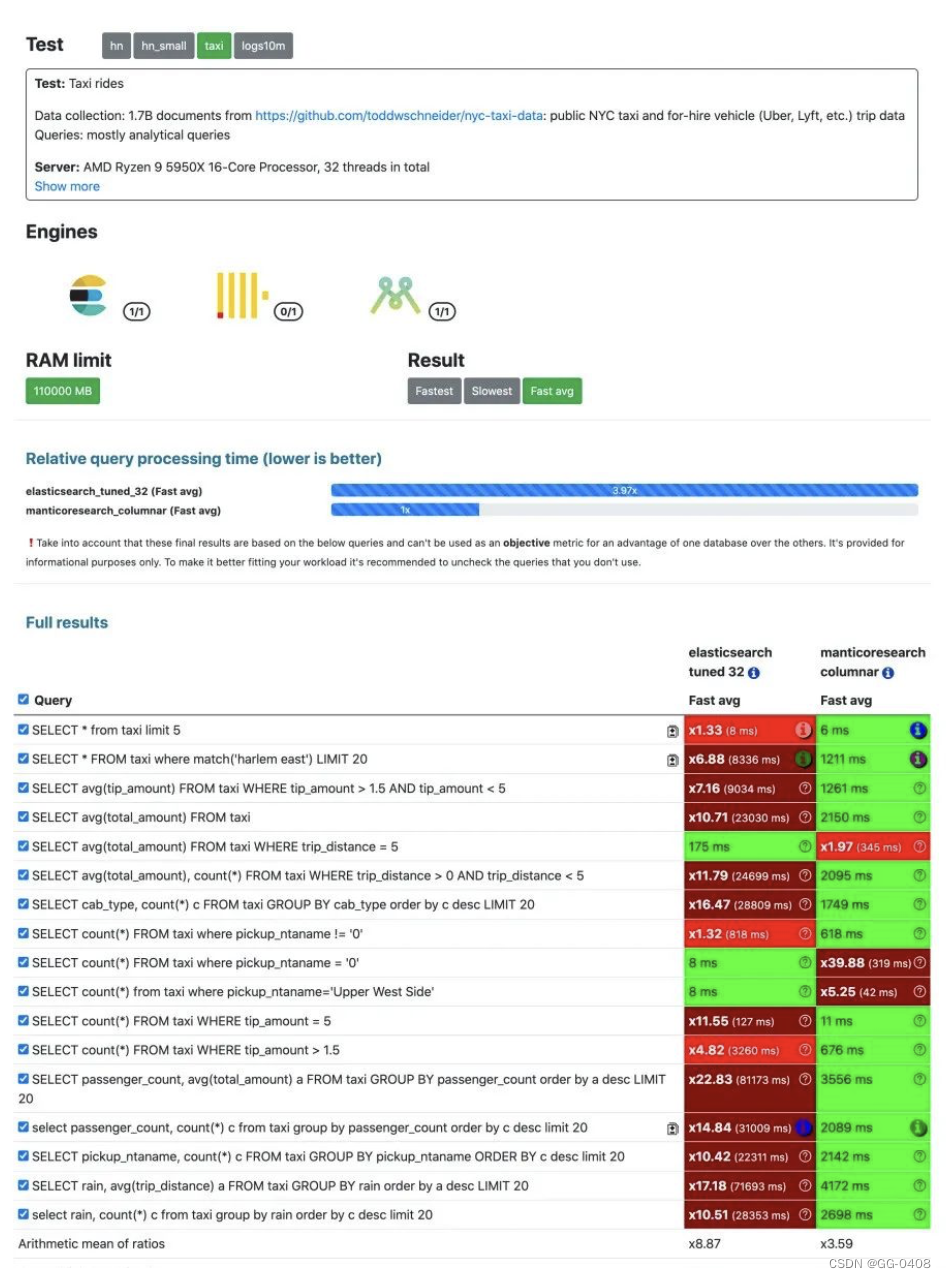
探索Manticore Search:开源全文搜索引擎的强大功能
在当今信息爆炸的时代,数据的快速检索变得至关重要。无论是在电子商务网站、新闻门户还是企业内部文档,高效的搜索引擎都是确保用户满意度和工作效率的关键因素之一。而在搜索引擎领域,Manticore Search 作为一款开源的全文搜索引擎ÿ…...

AI 笔记助手,你的思路整理助手
大家好,今天给大家介绍一款非常实用的 AI 笔记助手——AI Note。这款助手就像是一个贴心的小助手,能帮助我们整理笔记,提高学习和工作效率。 🤖 AI Note 可以智能总结笔记内容,准确标记重点,让我们更快地获…...
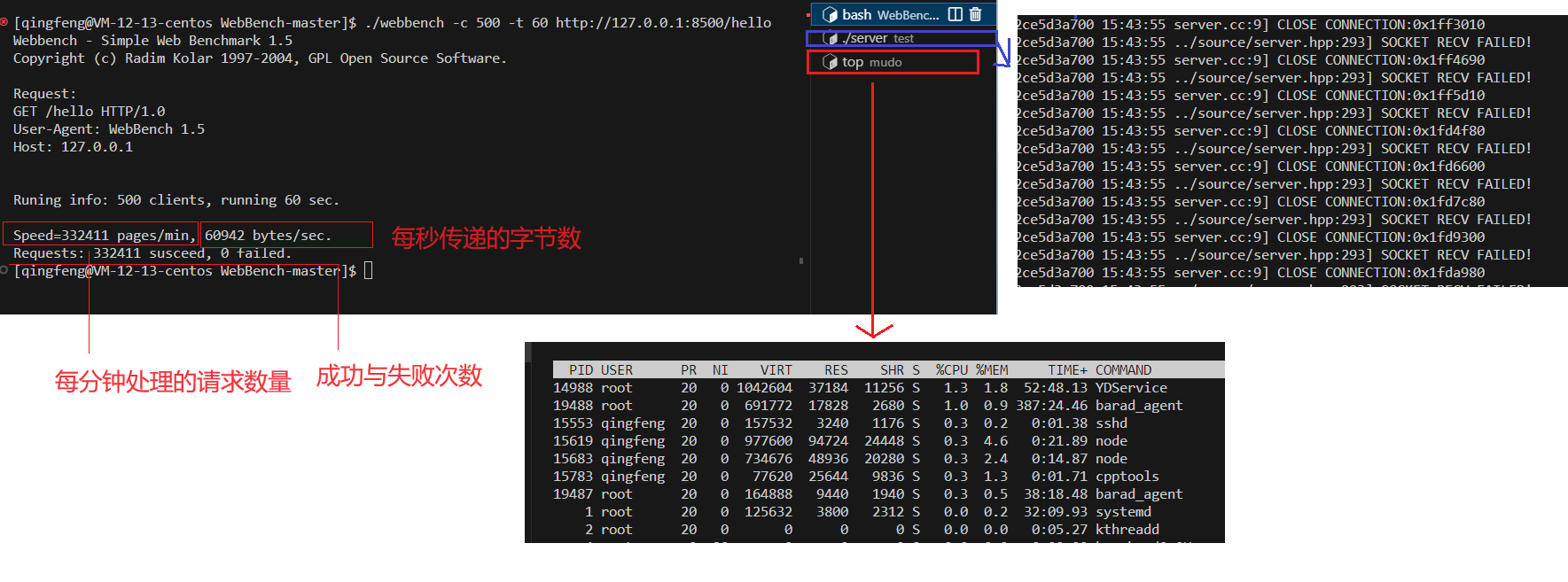
EchoServer回显服务器简单测试
目录 工具介绍 工具使用 测试结果 工具介绍 github的一个开源项目,是一个测压工具 EZLippi/WebBench: Webbench是Radim Kolar在1997年写的一个在linux下使用的非常简单的网站压测工具。它使用fork()模拟多个客户端同时访问我们设定的URL,测试网站在压力下工作的…...

车灯修复UV胶的优缺点有哪些?
车灯修复UV胶的优点如下: 优点: 快速固化:通过紫外光照射,UV胶可以在5-15秒内迅速固化,提高了修复效率。高度透明:固化后透光率高,几乎与原始车灯材料无法区分,修复后车灯外观更加…...
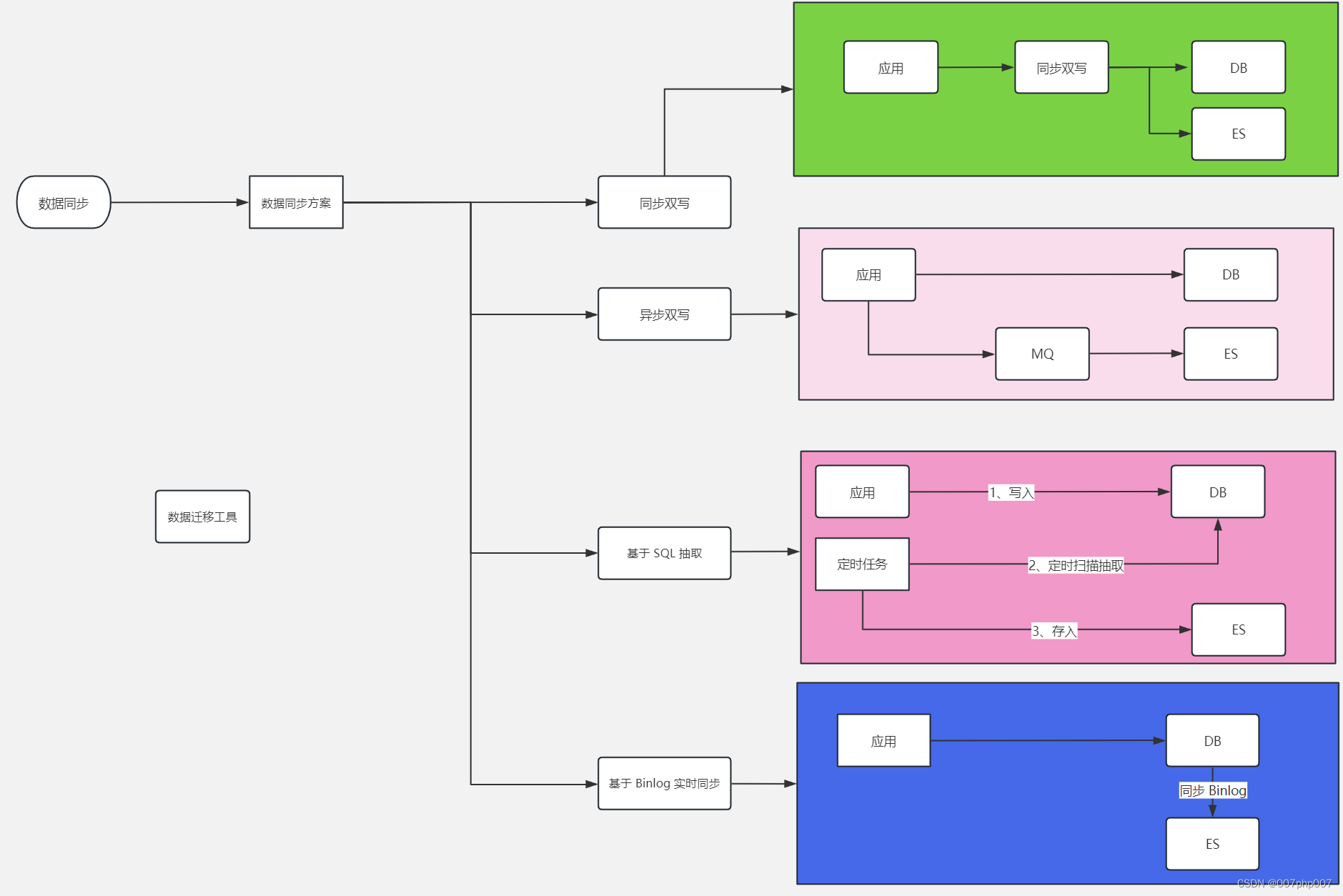
探讨倒排索引Elasticsearch面试与实战:从理论到实践
在当前大数据时代,Elasticsearch(以下简称为ES)作为一种强大的搜索和分析引擎,受到了越来越多企业的青睐。因此,对于工程师来说,掌握ES的面试准备和实战经验成为了必备技能之一。本文将从ES的面试准备和实际…...
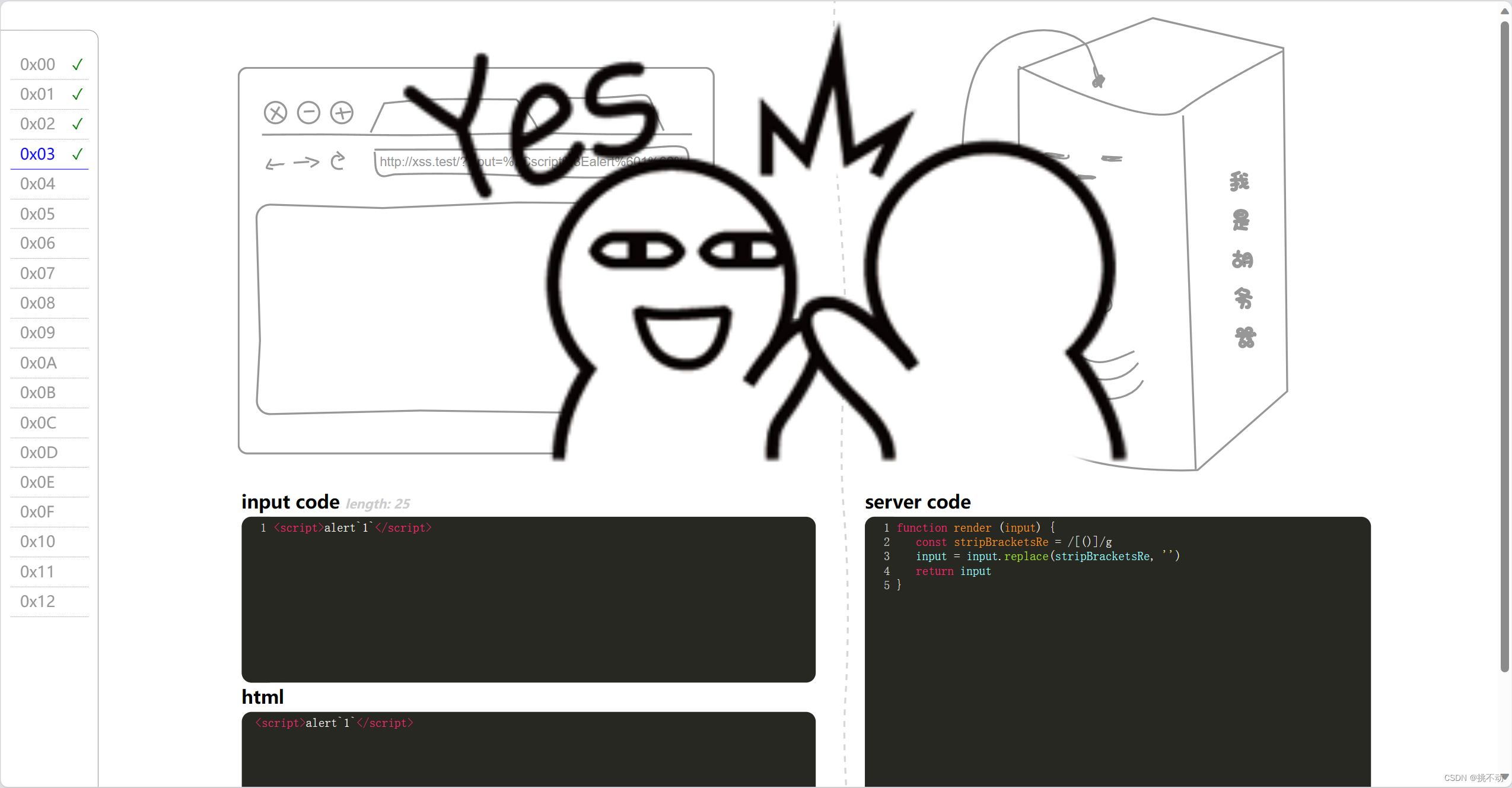
网安入门18-XSS(靶场实战)
HTML实体化编码 为了避免 XSS 攻击,会将<>编码为<与>,这些就是 HTML 实体编码。 编码前编码后不可分的空格 < (小于符号)< > (大于符号)> & (与符号)&″ (双引号)"’ (单引号)'© (版权符…...

爬虫的一些小技巧总结
一、在爬虫中,爬取的数据类型如下 1.document:返回的是一个HTML文档 2.png:无损的图片,jpg:压缩后的图片,wbep:有损压缩,比png差,比jpg好 3.avgxml图像编码字符串 4.script:脚本文件,依据一定格式编写的可执行的文…...

LeetCode---386周赛
题目列表 3046. 分割数组 3047. 求交集区域内的最大正方形面积 3048. 标记所有下标的最早秒数 I 3049. 标记所有下标的最早秒数 II 一、分割数组 这题简单的思维题,要想将数组分为两个数组,且分出的两个数组中数字不会重复,很显然一个数…...
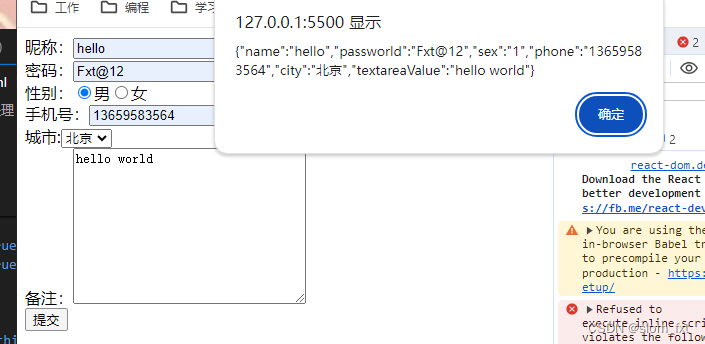
React之数据绑定以及表单处理
一、表单元素 像<input>、<textarea>、<option>这样的表单元素不同于其他元素,因为他们可以通过用户交互发生变化。这些元素提供的界面使响应用户交互的表单数据处理更加容易 交互属性,用户对一下元素交互时通过onChange回调函数来监听…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
