LeetCode---386周赛
题目列表
3046. 分割数组
3047. 求交集区域内的最大正方形面积
3048. 标记所有下标的最早秒数 I
3049. 标记所有下标的最早秒数 II
一、分割数组

这题简单的思维题,要想将数组分为两个数组,且分出的两个数组中数字不会重复,很显然一个数字出现次数最多两次,代码如下
class Solution {
public:bool isPossibleToSplit(vector<int>& nums) {unordered_map<int,int>mp;for(auto x:nums)if(++mp[x]>2)return false;return true;}
};二、求交集区域内的最大正方形面积

直接暴力枚举出所有两个矩阵的交集的正方形面积,求解出最大值,代码如下
class Solution {
public:long long largestSquareArea(vector<vector<int>>& bLeft, vector<vector<int>>& tRight) {int n=bLeft.size(),w=0;for(int i=1;i<n;i++){for(int j=i-1;j>=0;j--){//挑选四个直线,围成交集区域int x_l=max(bLeft[i][0],bLeft[j][0]);int x_r=min(tRight[i][0],tRight[j][0]);int y_top=min(tRight[i][1],tRight[j][1]);int y_bottom=max(bLeft[i][1],bLeft[j][1]);if(x_l<x_r&&y_top>y_bottom){//确保会有交集w=max(w,min(x_r-x_l,y_top-y_bottom));}} }return 1LL*w*w;}
};三、标记所有下标的最早秒数I

题目问最早秒数,我们正常来说都会想到贪心 / 从小到大枚举验证,其中贪心,大家可以去试着想想,因为需要从左往右遍历时间,而我们不知道后面changeIndices[]的情况,所以就不能去决定这一步去做什么操作会比较好,也就很难去贪心。
那么我们来看看枚举验证行不行?一旦数据不好,估计得验证O(n)次,大概率会超时,所以我们要降低时间复杂度,怎么做?--- 二分
1、是否满足二分条件,即单调性?
根据题目所给的条件,我们知道时间越多,我们越有可能将nums[i]减为零,越有可能标记所有下标,即秒数越多越能满足条件,符合单调性,可以二分
2、如何验证是否能在k秒内标记所有下标,即bool check(int k)函数如何写?(如果下面的内容不理解,可以先看看下面加粗的内容)
首先,由于changeIndices[]是不可预知的,即标记操作是不可控的,所以我们优先考虑什么时候标记下标的问题,根据贪心,我们肯定是越晚标记下标越好,这样会有更多的时间将nums[i]减为零,所以我们要知道每个下标的最晚标记时间
然后在来考虑是否能在下标 i 的最晚标记时间之前,将nums[i]减为零,这个就很简单了,我们只要维护一个cnt来记录到目前为止有多少时间,然后在到达某个最晚标记时间时,如果cnt>=nums[i],cnt = cnt - nums[i],否则直接返回false,如果所有下标都能被标记就返回true (很显然check函数的时间复杂度为O(n),所以暴力枚举会超时,需要二分)
如果大家不是很理解,可以将这题转换成考试来看,即一共有n门课程,nums[i]表示第 i 门课程的复习天数,changeIndices[i]表示第 i 天进行考试的课程,问复习完并考完所有课程的最少天数是多少?相信经历了这么多年考试的你们,会更容易理解复习和考试的关系(doge)
代码如下
/*
将问题转换成一共有n门课程,第i门课程的复习时间为nums[i]天
changeIndices[i]课程的考试时间为第i天
复习并考完所有课程的最小时间由于考试时间是固定的,我们需要优先考虑考试时间
=> 考试时间越靠后,就会有更加充分的时间用来复习
=> 具有单调性
=> 可以二分check函数如何去判断是否能复习考完所有的考试?
1、贪心,我们把每门课程的考试时间尽可能往后拖延 last[]记录每门课程的最迟考试时间
2、如果考试数目<=课程数,return false; // 可以优化的点否则我们从前往后遍历天数,优先复习考试时间近的科目,看能否在考试之前完成复习
*/class Solution {
public:int earliestSecondToMarkIndices(vector<int>& nums, vector<int>& changeIndices) {int n=nums.size(),m=changeIndices.size();auto check=[&](int k)->bool{vector<int>last(n,-1); // 记录下标i的最晚标记时间,即最晚考试时间for(int i=0;i<k;i++)last[changeIndices[i]-1]=i;for(auto x:last)if(x<0) // 表示有的下标没有被标记的时间,即有的课程没有考试return false;int cnt = 0;for(int i=0;i<k;i++){int idx = changeIndices[i] - 1;if(last[idx]==i){//表示下标idx到了最后的被标记的时间,即课程到了考试的最后截止时间cnt-=nums[idx];if(cnt<0) return false;//没有足够的时间将nums[idx]置为0,即没有足够的时间复习课程}else{cnt++;}}return true;};int l=1,r=m;while(l<=r){int mid = l+(r-l)/2;if(check(mid)) r=mid-1;else l=mid+1;}return l>m?-1:l;}
};四、标记所有下标的最早秒数II

有情提醒一下: 该题和第三题的题目并不一样。
在这题中,操作变得更加复杂了,但其实我们还是可以借鉴第三题的思路:
首先,这题依旧能够二分,因为时间越多,越有可能标记所有下标,但是check函数的思路不一样了,我们要优先考虑清零操作,因为它是不可控的(为了方便描述,这里将题目中的几个操作分别称为减一、清零、标记)。
【如果下面的内容看不太明白,依旧可以带入上一题说的考试模型,帮助你理解---减一操作:花费一天复习一门课,清空操作:花费一天速通一门课,标记:选择一天用来考试】
1)这里就要讨论一下:清零操作和减一操作什么时候用比较合适?
1、如果nums[i]用过减一操作,还需要用清零操作吗?没必要,因为如果能清零,就没必要在花多余的时间进行减一,可以将多出的时间给其他的nums[j]
2、如果nums[i]用过清零操作,也就不需要在进行减一操作了
结论:对于nums[i]要么执行清零操作,要么就执行减一操作,不能混用
2)根据贪心:我们肯定是能清零就尽量的去执行清零,让被清零的nums[i]有更多的时间被减为0
1、清零操作是越早越好还是越晚越好?肯定是越早越好,因为我们还需要有多余的时间去标记,所以我们需要从后往前遍历,去看是否有多余的时间去标记下标,所以我们要记录每个下标的最早清零时间
2、什么时候不需要用清零操作?
- nums[i]==0时,不需要
- nums[i]==1时,也不需要,因为减一操作也能做到清零,且可以在任意时间执行
除了上面的两种情况,还有一种特殊的情况,即用完清零操作之后就没时间进行标记了,这里我们不是只能进行对 i 下标进行nums[i]次减一操作,而是可以看之前进行清空操作的下标中nums[j]的最小值 是否 比nums[i]小,如果小,那么显然我们可以对 j 下标进行nums[j]次减一操作,同时nums[i]就会有时间进行清零和标记,这样的方案显然会更优----反悔贪心
我们从后往前遍历,同时维护用来标记/减一的时间cnt 和 需要减一和标记的总时间sum(都不包含进行清零操作的下标的标记时间)具体如何维护看下面的代码。
class Solution {
public:int earliestSecondToMarkIndices(vector<int>& nums, vector<int>& changeIndices) {int n=nums.size(),m=changeIndices.size();long long total = n;for(auto x:nums) total += x; vector<int>first_d(n,-1);for(int i=m-1;i>=0;i--)first_d[changeIndices[i]-1]=i;auto check=[&](int k)->bool{priority_queue<int,vector<int>,greater<int>> q;int cnt = 0;// 减一复习并考试的课程的所有时间long long slow = total;//记录减一操作的nums[i]及其标记需要的时间,一开始默认全用减一操作for(int i=k-1;i>=0;i--){int idx=changeIndices[i]-1;if(nums[idx]<=1||i!=first_d[idx]){cnt++;continue;}if(cnt==0){if(q.empty()||nums[idx]<=q.top()){//只能进行减一操作cnt++;continue;}slow += q.top()+1;q.pop();cnt += 2;}slow -= nums[idx]+1;cnt--;q.push(nums[idx]);}return cnt>=slow;};int l=1,r=m;while(l<=r){int mid=l+(r-l)/2;if(check(mid)) r=mid-1;else l=mid+1;}return l>m?-1:l;}
};相关文章:

LeetCode---386周赛
题目列表 3046. 分割数组 3047. 求交集区域内的最大正方形面积 3048. 标记所有下标的最早秒数 I 3049. 标记所有下标的最早秒数 II 一、分割数组 这题简单的思维题,要想将数组分为两个数组,且分出的两个数组中数字不会重复,很显然一个数…...
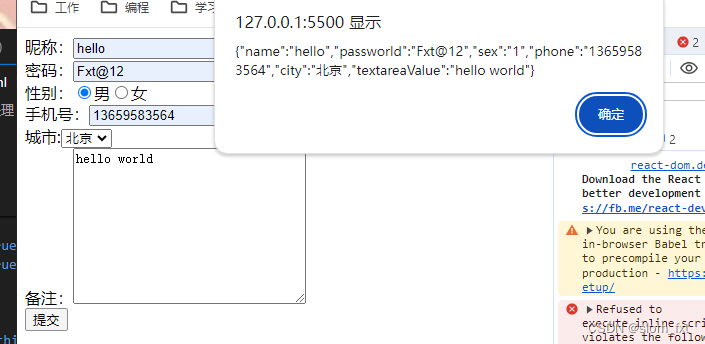
React之数据绑定以及表单处理
一、表单元素 像<input>、<textarea>、<option>这样的表单元素不同于其他元素,因为他们可以通过用户交互发生变化。这些元素提供的界面使响应用户交互的表单数据处理更加容易 交互属性,用户对一下元素交互时通过onChange回调函数来监听…...
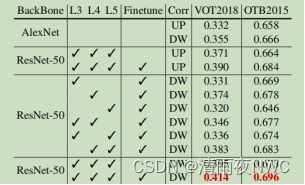
Siamrpn++论文中文翻译(详细!)
SiamRPN: Evolution of Siamese Visual Tracking with Very Deep Networks SiamRPN:具有非常深度网络的Siamese视觉跟踪的进化 【siamrpn论文地址】 https://arxiv.org/abs/1812.11703 摘要 基于Siamese网络的跟踪器将跟踪表示为目标模板和搜索区域之间的卷积特征…...

第一篇【传奇开心果系列】Python的自动化办公库技术点案例示例:深度解读Pandas库
传奇开心果博文系列 系列博文目录Python的自动化办公库技术点案例示例系列 博文目录前言一、主要特点和功能介绍二、Series 示例代码三、DataFrame示例代码四、数据导入/导出示例代码五、数据清洗示例代码六、数据选择和过滤示例代码七、数据合并和连接示例代码八、数据分组和聚…...
基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的停车位检测系统(Python+PySide6界面+训练代码)
摘要:开发停车位检测系统对于优化停车资源管理和提升用户体验至关重要。本篇博客详细介绍了如何利用深度学习构建一个停车位检测系统,并提供了完整的实现代码。该系统基于强大的YOLOv8算法,并结合了YOLOv7、YOLOv6、YOLOv5的性能对比…...
)
状态模式(State Pattern)
定义 状态模式(State Pattern)是一种行为设计模式,它允许对象在其内部状态改变时改变其行为。这意味着,当对象的状态发生变化时,它的行为也会发生变化。状态模式特别适用于行为依赖于其状态的对象,而且当这…...

js之版本号排序
版本号排序 给定一个由版本号组成的数组,按照版本号由小到大排序 假如版本号如下 : ["0.1.1", "2.3.3", "0.302.1", "4.2", "4.3.5", "4.3.4.5"];原理很简单,通过自定义sort排…...

考取ORACLE数据库OCP的必要性 Oracle数据库
OCP证书是什么? OCP,全称Oracle Certified Professional,是Oracle公司的Oracle数据库DBA(Database Administrator,数据库管理员)认证课程。这是Oracle公司针对数据库管理领域设立的一项认证课程,旨在评估和…...
WordPress通过宝塔面板的入门安装教程【保姆级】
WordPress安装教程【保姆级】【宝塔面板】 前言一:安装环境二:提前准备三:域名解析四:开始安装五:安装成功 前言 此教程适合新手,即使不懂代码,也可轻松安装wordpress 一:安装环…...

Leetcoder Day25| 回溯part05:子集+排列
491.递增子序列 给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。 示例: 输入:[4, 7, 6, 7]输出: [[4, 6], [4, 7], [4, 6, 7], [6, 7], [7,7], [4,7,7]] 说明: 给定数组的长度不会超过15。数组中的整数范围是 [-100,100]。给定数…...

【HTML】HTML基础5(特殊字符)
目录 特殊字符的作用 常用的特殊字符 使用效果 特殊字符的作用 例如 当我在两个文字间打出空格时 <p>“银河护卫队”系列 在漫威电影宇宙中一直是异数般的存在,不仅因为影片主角是一群反英雄,<strong>与超级英雄相比显得格格不入<…...

MacBook将iPad和iPhone备份到移动硬盘
#创作灵感# 一个是ICloud不够用,想备份到本地;然而本地存储不够用,增加容量巨贵,舍不得这个钱,所以就想着能不能备份到移动硬盘。刚好有个移动固态,所以就试了一下,还真可以。 #正文# 说一下逻…...
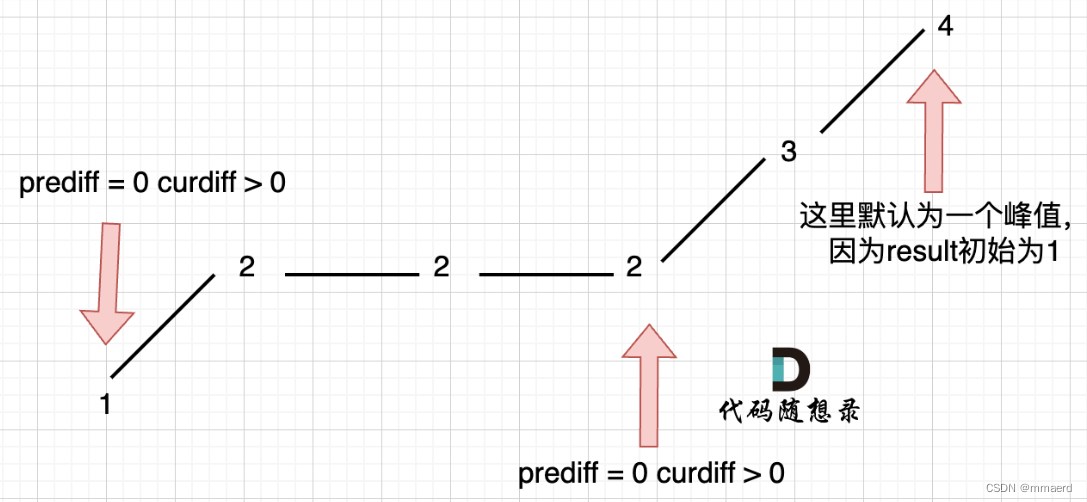
贪心 Leetcode 376 摆动序列
摆动序列 Leetcode 376 学习记录自代码随想录 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如&#…...
)
蓝桥杯(3.1)
92. 递归实现指数型枚举 import java.util.Scanner;public class Main {static int N 16;static int n;static int[] st new int[N]; public static void dfs(int u) {if(u > n) {for(int i1;i<n;i) {if(st[i] 1)System.out.print(i" ");}System.out.print…...

像用Excel一样用Python:pandasGUI
文章目录 启动数据导入绘图 启动 众所周知,pandas是Python中著名的数据挖掘模块,以处理表格数据著称,并且具备一定的可视化能力。而pandasGUI则为pandas打造了一个友好的交互窗口,有了这个,就可以像使用Excel一样使用…...

C#面:Application , Cookie 和 Session 会话有什么不同
Application、Cookie 和 Session 是在Web开发中常用的三种会话管理方式 Application(应用程序): Application 是在服务器端保存数据的一种方式,它可以在整个应用程序的生命周期内共享数据。Application 对象是在应用程序启动时创…...
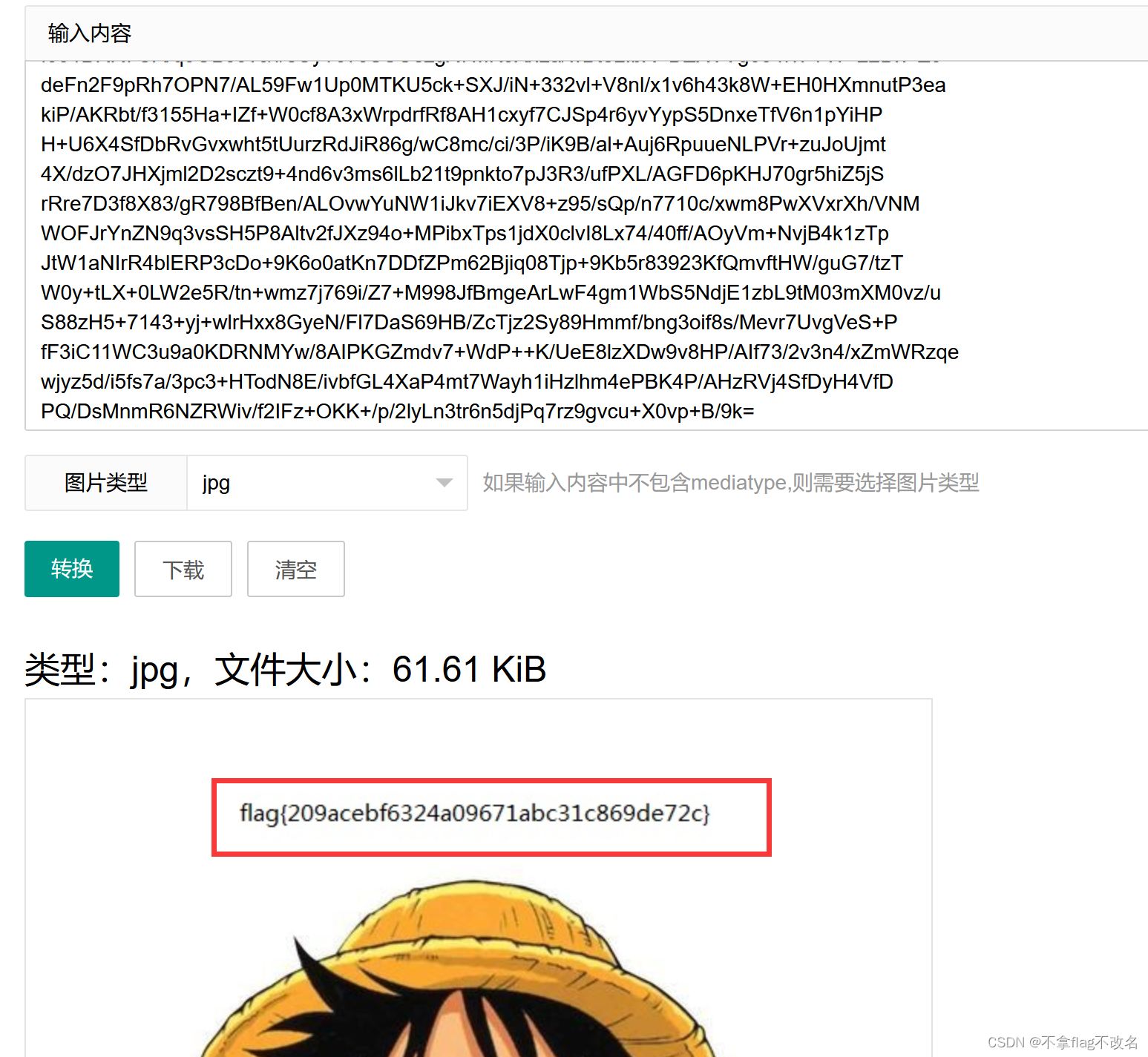
BUUCTF---数据包中的线索1
1.题目描述 2.下载附件,是一个.pcap文件 3.放在wireshark中,仔细观察数据流,会发现有个叫fenxi.php的数据流 4.这条数据流是http,且使用GET方式,接下来我们使用http.request,methodGET 命令来过滤数据流 5.在分析栏中我们追踪htt…...

【数仓】kafka软件安装及集群配置
相关文章 【数仓】基本概念、知识普及、核心技术【数仓】数据分层概念以及相关逻辑【数仓】Hadoop软件安装及使用(集群配置)【数仓】Hadoop集群配置常用参数说明【数仓】zookeeper软件安装及集群配置 一、环境准备 准备3台虚拟机 Hadoop131ÿ…...
代码随想录 二叉树第三周
目录 404.左叶子之和 513.找树左下角的值 112.路径总和 106.从中序与后序遍历构造二叉树 105.从前序与中序遍历序列构造二叉树 654.最大二叉树 404.左叶子之和 404. 左叶子之和 简单 给定二叉树的根节点 root ,返回所有左叶子之和。 示例 1: 输…...

flask流式输出-SSE服务
一、定义 flask demo前端遇到的问题 二、实现 flask demo from gevent import monkey monkey.patch_all() #并行 import time from flask import Response, stream_with_context from flask import Flask from gevent.pywsgi import WSGIServer from flask import …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
