代码随想录 二叉树第三周
目录
404.左叶子之和
513.找树左下角的值
112.路径总和
106.从中序与后序遍历构造二叉树
105.从前序与中序遍历序列构造二叉树
654.最大二叉树
404.左叶子之和
404. 左叶子之和
简单
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
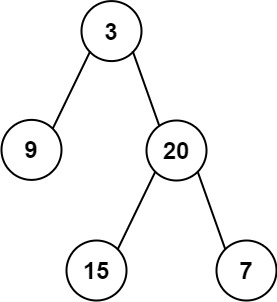
输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1] 输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
递归法
定义一个前驱指针指向要处理的节点的父节点,此时可判断该节点是否是左子节点
/*** Definition for a binary tree node.* 二叉树节点的定义* public class TreeNode {* int val; // 节点值* TreeNode left; // 左子节点* TreeNode right; // 右子节点* TreeNode() {} // 默认构造函数* TreeNode(int val) { this.val = val; } // 带值的构造函数* TreeNode(int val, TreeNode left, TreeNode right) { // 带值和子节点的构造函数* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {// 计算左叶子节点的和public int sumOfLeftLeaves(TreeNode root) {// 初始调用 leftLeavesSum 方法,传入 null 作为前一个节点int sum = leftLeavesSum(null, root); return sum; // 返回左叶子节点的和}// 递归计算左叶子节点的和public int leftLeavesSum(TreeNode pre, TreeNode root) {if(root == null){ // 如果当前节点为空,返回 0return 0;}int middleSum = 0; // 用于累加左叶子节点的和// 如果当前节点是左叶子节点且前一个节点不为空且是当前节点的父节点if(root.left == null && root.right == null && pre != null && pre.left == root){middleSum += root.val; // 将当前节点值加入到左叶子节点的和中return middleSum; // 返回当前节点值作为左叶子节点的和}// 递归计算左子树的左叶子节点的和int leftSum = leftLeavesSum(root, root.left);// 递归计算右子树的左叶子节点的和int rightSum = leftLeavesSum(root, root.right);// 返回左叶子节点的和,包括左子树、右子树和当前节点的和return middleSum + leftSum + rightSum;}
}
迭代法
// 层序遍历迭代法
class Solution {public int sumOfLeftLeaves(TreeNode root) {int sum = 0; // 初始化左叶子节点的和if (root == null) return 0; // 如果根节点为空,返回0Queue<TreeNode> queue = new LinkedList<>(); // 创建一个队列用于层序遍历queue.offer(root); // 将根节点加入队列while (!queue.isEmpty()) { // 当队列不为空时,继续遍历int size = queue.size(); // 获取当前层的节点数while (size-- > 0) { // 遍历当前层的所有节点TreeNode node = queue.poll(); // 从队列中取出一个节点if (node.left != null) { // 如果左节点不为空queue.offer(node.left); // 将左节点加入队列if (node.left.left == null && node.left.right == null){ // 判断左节点是否为叶子节点sum += node.left.val; // 如果是左叶子节点,则将其值加入到和中}}if (node.right != null) queue.offer(node.right); // 将右节点加入队列}}return sum; // 返回左叶子节点的和}
}
513.找树左下角的值
513. 找树左下角的值
中等
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
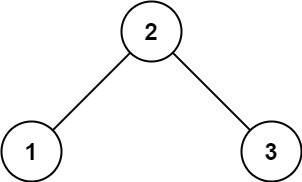
输入: root = [2,1,3] 输出: 1
示例 2:
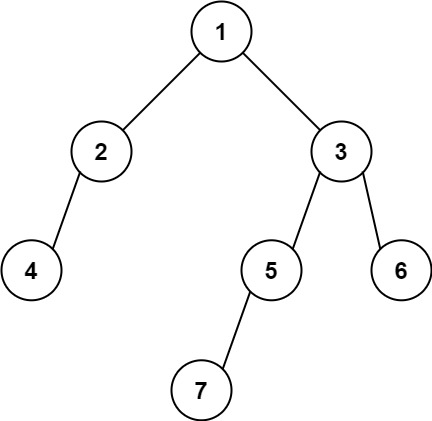
输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
递归法:
同一深度的情况下,由于左子树先于右子树遍历,故左侧节点先被更新到value中,而同一层其他节点不会被更新
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/// 解题思路:
// 使用深度优先搜索(DFS)来遍历二叉树,记录最左侧叶子节点的值以及其深度,
// 若当前叶子节点的深度大于已记录的最大深度,则更新最左侧叶子节点的值和深度,
// 最终返回最左侧叶子节点的值。class Solution {int maxDepth = -1; // 初始化最大深度为-1int value = 0; // 初始化最左侧叶子节点的值为0public int findBottomLeftValue(TreeNode root) {leftValue(root, 0); // 调用递归函数return value; // 返回最左侧叶子节点的值}// 递归函数,用于寻找最左侧叶子节点的值public void leftValue(TreeNode root, int depth) {if (root == null) { // 如果当前节点为空,直接返回return;}if (root.left == null && root.right == null && depth > maxDepth) { // 当前节点为叶子节点且深度大于最大深度value = root.val; // 更新最左侧叶子节点的值maxDepth = depth; // 更新最大深度}leftValue(root.left, depth + 1); // 递归遍历左子树,深度加1leftValue(root.right, depth + 1); // 递归遍历右子树,深度加1}
}
迭代法
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution { // findBottomLeftValue方法,接受一个二叉树的根节点作为参数,返回最底层最左边节点的值。 public int findBottomLeftValue(TreeNode root) { // 创建一个队列,用于层序遍历二叉树。 Queue<TreeNode> queue = new LinkedList<>(); // 将根节点加入队列。 queue.offer(root); // 初始化结果变量,用于存储最底层最左边节点的值。 int res = 0; // 当队列不为空时,进行循环。 while (!queue.isEmpty()) { // 获取当前层的节点数量。 int size = queue.size(); // 遍历当前层的所有节点。 for (int i = 0; i < size; i++) { // 取出队列中的一个节点。 TreeNode poll = queue.poll(); // 如果是当前层的第一个节点(即最左边的节点),则更新结果变量的值。 if (i == 0) { res = poll.val; } // 如果该节点有左子节点,则将左子节点加入队列。 if (poll.left != null) { queue.offer(poll.left); } // 如果该节点有右子节点,则将右子节点加入队列。 if (poll.right != null) { queue.offer(poll.right); } } } // 返回结果变量的值,即最底层最左边节点的值。 return res; }
}112.路径总和
112. 路径总和
简单
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
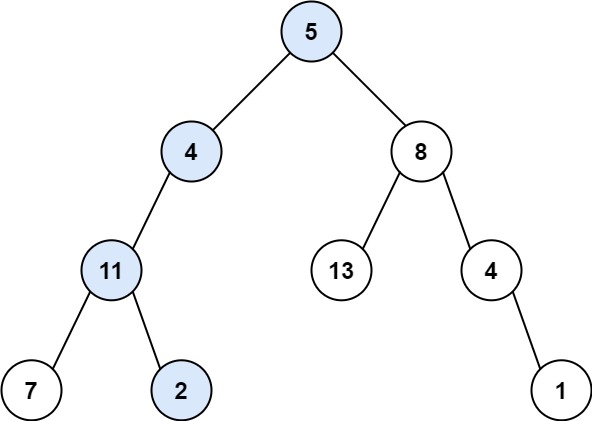
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
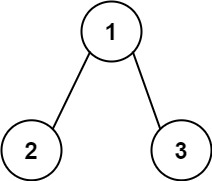
输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
递归法:
采用前序遍历,没到一个节点就将targetSum减去该节点的val,如果是根节点的话判断条件并返回,不是根节点的话向左右子树遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
// 定义一个Solution类
class Solution { // hasPathSum方法,接受一个二叉树的根节点root和一个目标值targetSum作为参数 // 返回值为boolean类型,表示是否存在从根节点到叶子节点的路径,使得路径上所有节点的值之和等于targetSum public boolean hasPathSum(TreeNode root, int targetSum) { // 如果根节点为空(即二叉树为空树),则不存在任何路径,返回false if(root == null){ return false; } // 从目标值中减去当前节点的值,更新目标值 targetSum -= root.val; // 如果当前节点是叶子节点(即没有左子节点和右子节点) if(root.left == null && root.right == null){ // 如果更新后的目标值为0,说明从根节点到当前叶子节点的路径上所有节点的值之和正好等于targetSum if(targetSum == 0){ return true; }else{ // 如果不等于0,则说明不存在符合条件的路径,返回false return false; } } // 如果当前节点不是叶子节点,则递归地对左子树和右子树调用hasPathSum方法 // leftResult表示左子树中是否存在符合条件的路径 boolean leftResult = hasPathSum(root.left,targetSum); // rightResult表示右子树中是否存在符合条件的路径 boolean rightResult = hasPathSum(root.right,targetSum); // 如果左子树或右子树中存在符合条件的路径,则返回true;否则返回false return leftResult || rightResult; }
}迭代法:
// 定义一个Solution类
class Solution { // hasPathSum方法,接受一个二叉树的根节点root和一个目标值targetSum作为参数 // 返回值为boolean类型,表示是否存在从根节点到叶子节点的路径,使得路径上所有节点的值之和等于targetSum public boolean hasPathSum(TreeNode root, int targetSum) { // 如果根节点为空(即二叉树为空树),则不存在任何路径,返回false if(root == null){ return false; } // 创建两个队列,一个用于存储节点,另一个用于存储从根节点到当前节点的路径和 Queue<TreeNode> treeNode = new LinkedList<>(); Queue<Integer> count = new LinkedList<>(); // 将根节点和初始的路径和(即目标值)加入队列 treeNode.offer(root); count.offer(targetSum); // 使用while循环进行层序遍历,直到节点队列或路径和队列为空 while(!treeNode.isEmpty() && !count.isEmpty()){ // 取出队列中的节点和对应的路径和 TreeNode node = treeNode.poll(); int countRes = count.poll() - node.val; // 更新路径和,减去当前节点的值 // 如果当前节点是叶子节点(即没有左子节点和右子节点),并且路径和等于0 // 则说明找到了一个从根节点到叶子节点的路径,其路径上所有节点的值之和等于targetSum if(node.left == null && node.right == null && countRes == 0){ return true; } // 如果当前节点有左子节点,则将左子节点和更新后的路径和加入队列 if(node.left != null){ treeNode.offer(node.left); count.offer(countRes); } // 如果当前节点有右子节点,则将右子节点和更新后的路径和加入队列 if(node.right != null){ treeNode.offer(node.right); count.offer(countRes); } } // 如果遍历完所有节点后仍未找到符合条件的路径,则返回false return false; }
}106.从中序与后序遍历构造二叉树
106. 从中序与后序遍历序列构造二叉树
已解答
中等
相关标签
相关企业
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
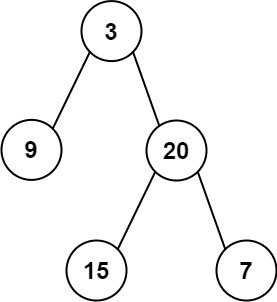
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {//因为每次都从postorder中取元素,所以当postorder为空的时候就返回nullif(postorder.length == 0){return null;} //取后序遍历的最后一个节点,即中,作为节点元素int nodeValue = postorder[postorder.length - 1];TreeNode node = new TreeNode(nodeValue);//找到后序数组最后一个元素在中序数组中的位置,即中间节点的位置,作为切割点int middleindex;for(middleindex = 0;middleindex < postorder.length - 1; middleindex ++){if(inorder[middleindex] == nodeValue){break;}}//切割中序数组,找到左子树的中序数组和右子树的中序数组//中间节点之前的,即左子树int[] leftInorder = Arrays.copyOfRange(inorder,0,middleindex);//中间节点之后的,即右子树int[] rightInorder = Arrays.copyOfRange(inorder,middleindex + 1,inorder.length);//切割后序数组,找到左子树的后序数组和右子树的后序数组//删除已经操作过的后序数组的最后一个元素postorder = Arrays.copyOfRange(postorder,0,postorder.length - 1);int[] leftPostorder = Arrays.copyOfRange(postorder,0,middleindex);int[] rightPostorder = Arrays.copyOfRange(postorder,middleindex,postorder.length);// 递归地构建左子树和右子树,并将它们分别设置为当前节点的左孩子和右孩子node.left = buildTree(leftInorder,leftPostorder);node.right = buildTree(rightInorder,rightPostorder);return node;}
}105.从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树
中等
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {//由于每次都是从前序数组中取元素,当前序数组为空时,返回nullif(preorder.length == 0){return null;}//当前序数组不为空时,从中取得第一个元素作为中间节点int nodeValue = preorder[0];TreeNode node = new TreeNode(nodeValue);//找到该中间节点(即第一个元素)在中序数组中的位置int middleIndex;for(middleIndex = 0;middleIndex < inorder.length - 1;middleIndex ++){if(inorder[middleIndex] == nodeValue){break;}}//切割中序数组,分为左子树的中序数组和右子树的中序数组int[] leftInorder = Arrays.copyOfRange(inorder,0,middleIndex);int[] rightInorder = Arrays.copyOfRange(inorder,middleIndex + 1,inorder.length);//切割前序数组,分为左子树的前序数组和右子树的前序数组//先删除数组中已经取出的中间节点preorder = Arrays.copyOfRange(preorder,1,preorder.length);int[] leftPreorder = Arrays.copyOfRange(preorder,0,middleIndex);int[] rightPreorder = Arrays.copyOfRange(preorder,middleIndex,preorder.length);// 递归地构建左子树和右子树,并将它们分别设置为当前节点的左孩子和右孩子node.left = buildTree(leftPreorder,leftInorder);node.right = buildTree(rightPreorder,rightInorder);return node;}
}654.最大二叉树
654. 最大二叉树
中等
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
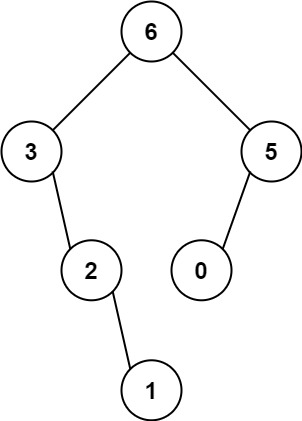
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
示例 2:
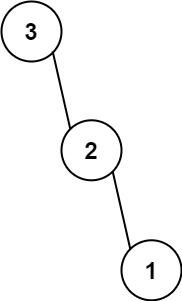
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000nums中的所有整数 互不相同
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution { // 返回构建好的最大二叉树的根节点 public TreeNode constructMaximumBinaryTree(int[] nums) { // 如果数组为空,则返回null,因为不能构建二叉树 if(nums.length == 0){ return null; } // 初始化最大值和最大值的索引为-1和0 int max = -1; int maxIndex = 0; // 遍历数组,找到最大值及其索引 for(int i = 0; i < nums.length; i++){ if(nums[i] > max){ max = nums[i]; maxIndex = i; } } // 创建一个新的树节点,值为数组中的最大值 TreeNode node = new TreeNode(max); // 使用Arrays类的copyOfRange方法,复制最大值左边的部分数组作为左子树的输入数组 int[] leftNums = Arrays.copyOfRange(nums, 0, maxIndex); // 使用Arrays类的copyOfRange方法,复制最大值右边的部分数组作为右子树的输入数组 int[] rightNums = Arrays.copyOfRange(nums, maxIndex + 1, nums.length); // 递归地构建左子树和右子树,并将它们分别设置为当前节点的左孩子和右孩子 node.left = constructMaximumBinaryTree(leftNums); node.right = constructMaximumBinaryTree(rightNums); // 返回构建好的最大二叉树的根节点 return node; }
}相关文章:

代码随想录 二叉树第三周
目录 404.左叶子之和 513.找树左下角的值 112.路径总和 106.从中序与后序遍历构造二叉树 105.从前序与中序遍历序列构造二叉树 654.最大二叉树 404.左叶子之和 404. 左叶子之和 简单 给定二叉树的根节点 root ,返回所有左叶子之和。 示例 1: 输…...

flask流式输出-SSE服务
一、定义 flask demo前端遇到的问题 二、实现 flask demo from gevent import monkey monkey.patch_all() #并行 import time from flask import Response, stream_with_context from flask import Flask from gevent.pywsgi import WSGIServer from flask import …...

注解整理ing
注解 1. 实体类注解 Data注解是lombok.jar包下的注解,该注解通常用在实体bean上,不需要写出set和get方法 Data相当于Getter Setter RequiredArgsConstructor ToString EqualsAndHashCode这5个注解的合集 EqualsAndHashCode注解会生成equals(Object oth…...

Android 将图片网址url转化为bitmap
1. 图片网址url转化为bitmap 1.1. 方法一 通过 HttpURLConnection 请求 要使用一个线程去访问,因为是网络请求,这是一个一步请求,不能直接返回获取,要不然永远为null,在这里得到BitMap之后记得使用Hanlder或者EventBu…...

鸿蒙Harmony应用开发—ArkTS声明式开发(通用属性:颜色渐变)
设置组件的颜色渐变效果。 说明: 从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 linearGradient linearGradient(value: { angle?: number | string; direction?: GradientDirection; colors: Array; repea…...

腾讯云幻兽帕鲁游戏存档迁移教程,本地单人房迁移/四人世界怎么迁移存档?
腾讯云幻兽帕鲁游戏存档迁移的方法主要包括以下几个步骤: 登录轻量云控制台:首先,需要登录到轻量云控制台,这是进行存档迁移的前提条件。在轻量云控制台中,可以找到接收存档的服务器卡片,并点击进入实例详情…...

C2_W2_Assignment_吴恩达_中英_Pytorch
Neural Networks for Handwritten Digit Recognition, Multiclass In this exercise, you will use a neural network to recognize the hand-written digits 0-9. 在本次练习中,您将使用神经网络来识别0-9的手写数字。 Outline 1 - Packages 2 - ReLU Activatio…...

C语言实现航班管理
航班管理系统,用C语言实现,可以作为课程设计,代码如下: #include<iostream> #include<fstream> #include<vector> #include<string> #include<stdlib.h> using namespace std; //信息基类 clas…...

【Java面试题】SpringBoot与Spring的区别
主要区别体现几个方面: 1.操作简便性 SpringBoot提供极其快速和简化的操作,使得Spring开发者能更快速上手。它通过提供spring的运行配置,以及为通用spring项目提供许多非功能性特性,进一步简化了开发过程。 2.框架扩展性 Spri…...

网络编程(IP、端口、协议、UDP、TCP)【详解】
目录 1.什么是网络编程? 2.基本的通信架构 3.网络通信三要素 4.UDP通信-快速入门 5.UDP通信-多发多收 6.TCP通信-快速入门 7.TCP通信-多发多收 8.TCP通信-同时接收多个客户端 9.TCP通信-综合案例 1.什么是网络编程? 网络编程是可以让设…...
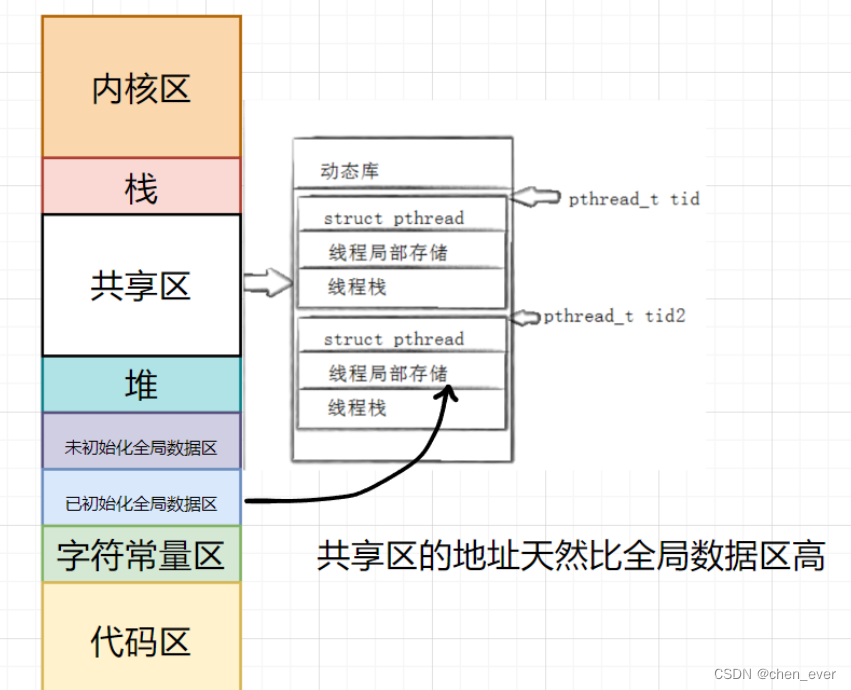
Linux线程(二)----- 线程控制
目录 前言 一、线程资源区 1.1 线程私有资源 1.2 线程共享资源 1.3 原生线程库 二、线程控制接口 2.1 线程创建 2.1.1 创建一批线程 2.2 线程等待 2.3 终止线程 2.4 线程实战 2.5 其他接口 2.5.1 关闭线程 2.5.2 获取线程ID 2.5.3 线程分离 三、深入理解线程 …...

Linux 内核irq_stack遍历
环境Centos 4.18.0-80.el8.x86_64 一、x86架构堆栈类型说明 https://www.kernel.org/doc/Documentation/x86/kernel-stacks int get_stack_info(unsigned long *stack, struct task_struct *task,struct stack_info *info, unsigned long *visit_mask) {if (!stack)goto unk…...

GIT问题记录
一、 1.Gitee相关 复现步骤:自己在gitee上使用WEB解决冲突,本地未拉取最新的origin分支,然后本地也做了其他的修改,然后commit并且push,push时候报错,本地分支不干净 尝试拉取origin的最新内容ÿ…...

AzerothCore安装记录
尝试在FreeBSD系统下安装AzerothCore 首先安装相关软件 pkg install cmake mysql80-server boost-all装完mysql之后提示: MySQL80 has a default /usr/local/etc/mysql/my.cnf, remember to replace it with your own or set mysql_optfile"$YOUR_CNF_FILE i…...
Infineon_TC264智能车代码初探及C语言深度学习(一)
本篇文章记录我在智能车竞赛中,对 Infineon_TC264 这款芯片的底层库函数的学习分析。通过深入地对其库函数进行分析,C语言深入的知识得以再次在编程中呈现和运用。故觉得很有必要在此进行记录一下。 目录 编辑 一、代码段 1、枚举类型 2、结构体 …...
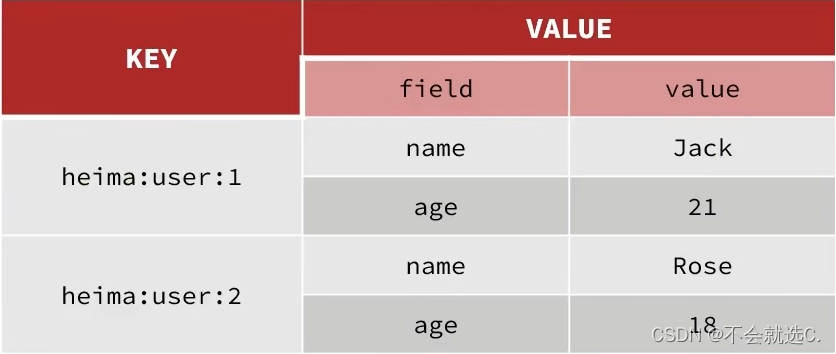
[Redis]——初识Redis
一、Redis为非关系型数据库 ❓我们常见的MySQL、SQLServer都是关系型数据库,那他们之间有什么区别与联系呢? 📕关系型数据库与非关系型数据库的区别(面试题) 解释: SQL数据库中的表是有结构的,包…...

YTM32的同步串行通信外设SPI外设详解(Master Part)
YTM32的同步串行通信外设SPI外设详解(Master Part) 文章目录 YTM32的同步串行通信外设SPI外设详解(Master Part)IntroductionFeatures引脚信号时钟源其它不常用功能 Pricinple & Mechinism基于FIFO的命令和数据管理机制锁定配…...

【C语言】三子棋
前言: 三子棋是一种民间传统游戏,又叫九宫棋、圈圈叉叉棋、一条龙、井字棋等。游戏规则是双方对战,双方依次在9宫格棋盘上摆放棋子,率先将自己的三个棋子走成一条线就视为胜利。但因棋盘太小,三子棋在很多时候会出现和…...
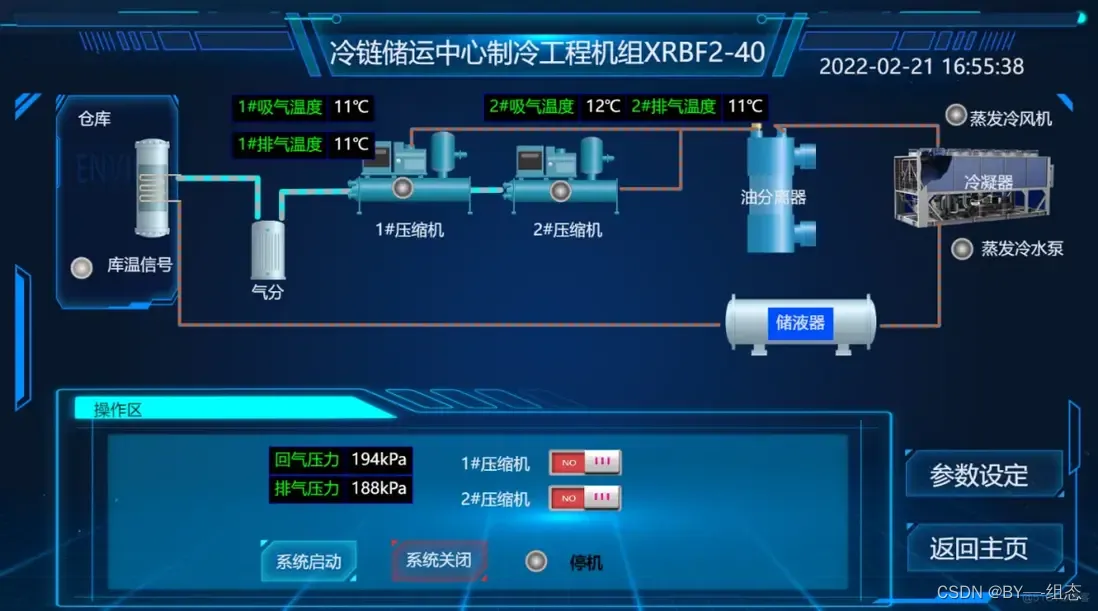
Web组态可视化编辑器 快速绘制组态
随着工业智能制造的发展,工业企业对设备可视化、远程运维的需求日趋强烈,传统的单机版组态软件已经不能满足越来越复杂的控制需求,那么实现Web组态可视化界面成为了主要的技术路径。 行业痛点 对于软件服务商来说,将单机版软件转变…...

WebServer -- 注册登录
目录 🍉整体内容 🌼流程图 🎂载入数据库表 提取用户名和密码 🚩同步线程登录注册 补充解释 代码 😘页面跳转 补充解释 代码 🍉整体内容 概述 TinyWebServer 中,使用数据库连接池实现…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
