python 基础知识点(蓝桥杯python科目个人复习计划56)
今日复习内容:做题
例题1:最小的或运算
问题描述:给定整数a,b,求最小的整数x,满足a|x = b|x,其中|表示或运算。
输入格式:
第一行包括两个正整数a,b;
输出格式:
输出共1行,包含一个整数,表示最终答案。
参考答案:
a,b = map(int,input().split())
print(a^b)运行结果:

以下是我对此题的理解:
1.因为题目要求找到一个最小的整数x,使得a|x = b|x,其中|x表示a和b的二进制形式对应位进行或运算;
2.从最高位开始比较,如果a和b在该位上的值相同(即都为0或都为1),那么x在该位上可以取任意值,不影响最终结果。因此,我们可以直接将该位的添加到结果x中。
3.如果在某一位上a和b的值不同(即一个为1,一个为0),那么为了使得a|x = b|x,我们需要将x在该位上的值设为1,因为1与任何数进行或运算都得到1。
4.最终,得到的x就是满足条件的最小整数
这种做法基于按位异或运算(^)的定义如下:
如果两个对应的二进制位相同,则结果为0;
如果两个对应的二进制位不同,则结果为1。
根据这个定义,当a和b的某一位不同时,按位异或的结果为1,这意味着在结果x的对应位上必须为1,否则无法满足条件。而当a,b的某一位相同时,按位异或的结果为0,这意味着在结果x的对应位上可以时0或1,都不影响最终结果。
因此用这个方法,可以得出答案。
例题2:简单的异或难题
问题描述:
最近蓝桥A梦喜欢上了或运算,特别是沉迷于异或运算。
异或运算的特殊之处在于,进行异或运算的两个数a和b,,对于它们在二进制下的同一位,只有两边数不相同,运算的结果才为1,如果相同,则为0。比如1和3进行运算,它们转化成二进制后,分别为01和11,那么它们的异或运算结果就是10,转换成十进制后就是2。
异或运算实在是太有趣了,他这些天一直在进行异或运算,蓝桥美怕他走火入魔了,打算给蓝桥A梦出个难题 打击一下他的兴趣。
蓝桥美给了蓝桥A梦n个正整数ai,然后进行m次询问,每次询问在第l个数到第r个数之间,所有出现次数为奇数的数的异或和是多少。
对于3个数a,b,c,它们的异或和就是:

这种难题怎么会难倒蓝桥A梦呢?他并不想回答这么简单的问题,所以他把问题扔给了你,你能解决吗?
输入格式:
第一行包括两个正整数n和m(1 <= n,m <= 1 * 10^5),表示数组的长度和询问的次数。
第二行包含n个正整数ai(1 <= ai <= 10^5),ai表示第i个位置上的数字是ai。
接下来m行,每行包含两个正整数l和r(1<= l,r <= n),表示当前询问的区间。
输出格式:
对于每一行询问,输出一个整数,为当前询问区间[l,r]的出现次数为奇数的数的异或和。
参考答案:
n,m = map(int,input().split())
a = list(map(int,input().split()))
pre = [0]
for i in range(n):pre.append(pre[-1]^a[i])
for i in range(m):l,r = map(int,input().split())print(pre[r]^pre[l - 1])运行结果:

以下是我对此题的理解:
n,m = map(int,input().split())
a = list(map(int,input().split()))
首先,读取输入,包括正整数的个数n,查询次数m以及正整数序列a;
pre = [0]
for i in range(n):
pre.append(pre[-1] ^ a[i])
使用一个数组pre来存储前缀异或和,其中pre[i]表示前i个数的异或和,这里pre的作用是为了方便计算任意区间的异或和。
在这个循环中,计算每个位置的前缀异或和,pre[-1]表示前i个数的异或和,然后再异或上当前数a[i],得到前i + 1个数的异或和,依次类推。
接下来就是读取查询区间[l,r]。
例题3:出列
问题描述:
上体育课时,n个同学按顺序站成一排,初始时第i个位置的同学,编号为i(从1开始)。
老师下令:“单数同学出列!”然后序号为单数的同学出列,剩下的同学重新按位置开始排列,编号不变。
老师又下令:“单数同学出列!”新的单数位置的同学出列,剩下的同学继续重新按位置排列。
如此下去,最后只剩下一个人,他的编号是多少?
输入格式:
输入仅一行,包含一个整数n。
输出格式:
输出仅一行,包含一个整数,表示最后剩下的人的编号。
参考答案:
n = int(input())
bin_n = bin(n)[2:]
print(1 << (len(bin_n) - 1))运行结果:

以下是我对此题的理解:
我刚开始想到的是数学归纳法:
首先观察一下题目,每次出列后,剩下的同学的编号会重新排列,但总是保持着奇数编号的同学被淘汰。当剩下的同学数量为奇数时,淘汰后剩下的同学编号从2开始重新编号。由此可以得出结论:之后剩下的同学编号一定是2的幂次方,因此,我们只需要找到,因此我们只需要找到小于等于n的最大的2的幂次方,就得到了答案。
首先,将输入的n转化为二进制字符字符串并去掉开头的‘0b’;
然后,通过len(bin_n) - 1计算二进制表示的n的位数;
最后,通过1 << (len(bin_n) - 1)得到最后的同学的编号,即为小于等于n的最大的2的幂次方;
bin(n)[2:]
将输入的n转化为二进制字符字符串并去掉开头的‘0b’
len(bin_n) - 1:计算二进制字符串的长度,即二进制的位数
1 << (len(bin_n) - 1):左移<<表示将1左移若干位,相当于乘以2的若干次方,这里左移的位数为二进制的位数减一,就是最后的那个学生的编号
然后,我就想到了另外一种方法:
n = int(input())# 寻找小于等于n的最大的2的幂次方
last_student = 1
while last_student <= n:last_student *= 2# 最后剩下的同学的编号即为小于等于n的最大的2的幂次方的一半
last_student //= 2print(last_student)例题4:位移
问题描述:
在一个神奇的玩具世界中,有两个小朋友,小明和小红,他们喜欢玩数字游戏。一天,他们发现了一种神奇的数字变换能力,只需使用位移运算(<<和>>)就能将一个数字变成另一个数字。
小明和小红决定进行一场数字变换的挑战。他们选定了两个数字a和b,并尝试通过位移运算讲数字a变成数字b。他们非常兴奋,想知道是否存在一系列的位移操作可以实现这个目标。
他们开始思考,并设计了各种位移操作的组合,希望能够将数字a变成数字b。如果他们成功找到一种位移操作组合,则输出Yes,否则输出No。
现在,让我们来帮小明和小红来完成这个数字变换的挑战,看看他们能否成功通过数字变换讲数字a变成数字b。
右移和左移的运算规则为:逻辑左移,高位丢弃,低位补0;逻辑 右移,低位丢弃,高位补0。如0000100,逻辑左移一位为0001000,逻辑右移一位为0000010。(需着重注意左移高位的变化)
输入描述:
第一行输入一个整数t,表示有t组测试数据;
接下来又t行输入,每行包含两个数字a和b,a和b意义如题目所述。
数据保证1 <= t <= 10^6,0 <= a,b <= 10^9
输出描述:
对于每一组测试数据,输出Yes或No。
参考答案:
import sys
t = int(input())
for i in range(t):a,b = map(int,sys.stdin.readline().strip('\n').split())bin_b = bin(b)[2:].strip('0')bin_a = bin(a)[2:]if bin_b in bin_a:print('Yes')else:print('No')运行结果:

以下是我对此题的理解:
这道题可以检查数字b的二进制表示是否是数字a的二进制表示的字符串的子串来解决。如果是,则说明存在一系列位移操作可以将数字a转换为数字b,否则不能。
以下是我的思路:
1.二进制表示的子串
当一个二进制数字b是另一个二进制数字a的子串时,意味着可以通过在数字a的二进制表示中通过位移操作来得到b,因为位移操作不会改变数字1和0的位置,只会改变它们的相对位置。
2.代码解析
首先输入测试用例的数量t;
然后通过一个循环处理每个测试用例,输入数字a和b;
接着,将a和b转化为二进制字符串;
然后检查数字b的二进制表示是否是数字a的二进制表示的字符串的字串;
如果是字串,则输出"Yes",说明存在一系列位移操作可以将a转换为b;
否则输出"No",说明不能通过位移操作将a转换为b。
OK,这篇就到这里,下一篇继续!
相关文章:

python 基础知识点(蓝桥杯python科目个人复习计划56)
今日复习内容:做题 例题1:最小的或运算 问题描述:给定整数a,b,求最小的整数x,满足a|x b|x,其中|表示或运算。 输入格式: 第一行包括两个正整数a,b; 输出格式&#…...

【vue】vue中数据双向绑定原理/响应式原理,mvvm,mvc、mvp分别是什么
关于 vue 的原理主要有两个重要内容,分别是 mvvm 数据双向绑定原理,和 响应式原理 MVC(Model-View-Controller): Model(模型):表示应用程序的数据和业务逻辑。View(视图&…...
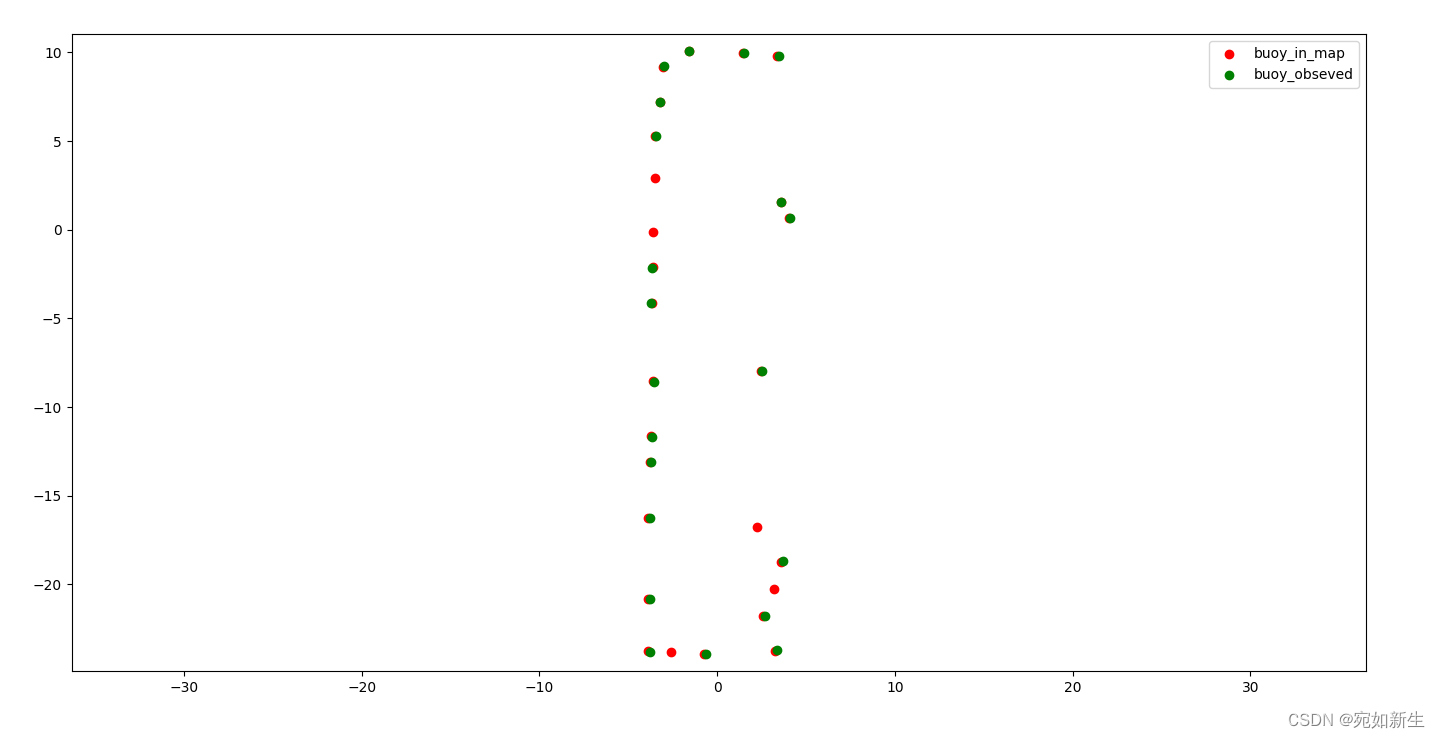
基于反光柱特征的激光定位算法思路
目录 1. 识别反光柱2. 数据关联2.1 基于几何形状寻找匹配2.2 暴力寻找匹配 3. 位姿估计(最小二乘求解)4. 问题4.1 精度问题4.2 快速旋转时定位较差 1. 识别反光柱 反光柱是特殊材料制成,根据激光雷达对反光材料扫描得到的反射值来提取特征。…...

CSM是什么意思?
CSM(Customer Service Management)是企业客户服务管理的信息化(IT)解决方案架构。本着以客户为中心的管理理念,搭建企业客户服务管理平台,实现企业以客户为中心的管理时代的竞争战略。 CSM的核心是以客户为中心,实现对…...

ES6 面试题
1. const、let 和 var 的区别是什么? 答案: var 声明的变量是函数作用域或全局作用域,而 const 和 let 声明的变量是块级作用域。使用 var 声明的变量可以被重复声明,而 const 和 let 不允许重复声明同一变量。const 声明的变量…...
智能指针(C++)
目录 一、智能指针是什么 二、为什么需要智能指针 三、智能指针的使用和原理 3.1、RALL 3.2 智能指针的原理 3.3、智能指针的分类 3.3.1、auto_ptr 3.3.2、unique_ptr 3.3.3、shared_ptr 3.2.4、weak_ptr 一、智能指针是什么 在c中,动态内存的管理式通过一…...

社区店商业模式探讨:如何创新并持续盈利?
在竞争激烈的商业环境中,社区店要想获得成功并持续盈利,需要不断创新和优化商业模式。 作为一名开鲜奶吧5年的创业者,我将分享一些关于社区店商业模式创新的干货和见解,希望能给想开实体店或创业的朋友们提供有价值的参考。 1、…...
一些可以访问gpt的方式
1、Coze扣子是新一代 AI 大模型智能体开发平台。整合了插件、长短期记忆、工作流、卡片等丰富能力,扣子能帮你低门槛、快速搭建个性化或具备商业价值的智能体,并发布到豆包、飞书等各个平台。https://www.coze.cn/ 2、https://poe.com/ 3、插件阿里…...

springer模板参考文献不显示
Spring期刊模板网站,我的问题是23年12月的版本 https://www.springernature.com/gp/authors/campaigns/latex-author-support/see-where-our-services-will-take-you/18782940 参考文献显示问好,在sn-article.tex文件中,这个sn-mathphys-num…...
【【C语言简单小题学习-1】】
实现九九乘法表 // 输出乘法口诀表 int main() {int i 0;int j 0;for (i 1; i < 9; i){for (j 1; j < i;j)printf("%d*%d%d ", i , j, i*j);printf("\n"); }return 0; }猜数字的游戏设计 #define _CRT_SECURE_NO_WARNINGS 1 #include<stdi…...

mongoDB 优化(1)索引
1、创建复合索引(多字段) db.collection_test1.createIndex({deletedVersion: 1,param: 1,qrYearMonth: 1},{name: "deletedVersion_1_param_1_qrYearMonth_1",background: true} ); 2、新增索引前: 执行查询: mb.r…...
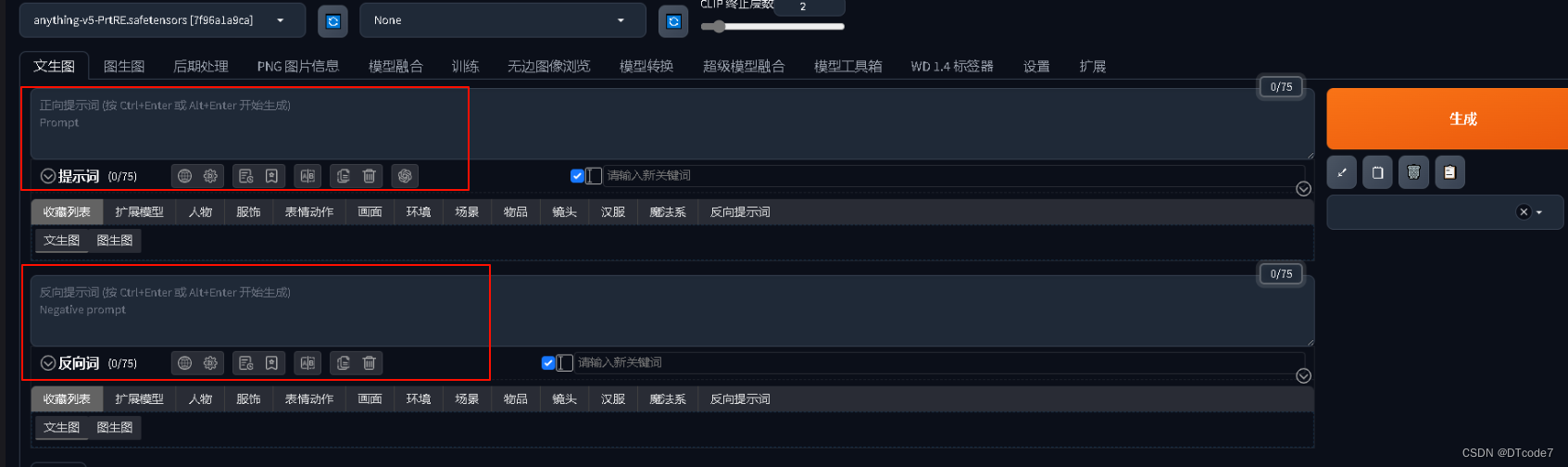
stable diffusion webUI之赛博菩萨【秋葉】——工具包新手安裝与使用教程
stable diffusion webUI之赛博菩萨【秋葉】——工具包新手安裝与使用教程 AI浪潮袭来,还是学习学习为妙赛博菩萨【秋葉】简介——(葉ye,四声,同叶)A绘世启动器.exe(sd-webui-aki-v4.6.x)工具包安…...

鸿蒙应用程序包安装和卸载流程
开发者 开发者可以通过调试命令进行应用的安装和卸载,可参考多HAP的调试流程。 图1 应用程序包安装和卸载流程(开发者) 多HAP的开发调试与发布部署流程 多HAP的开发调试与发布部署流程如下图所示。 图1 多HAP的开发调试与发布部署流程 …...

C语言数组全面解析:从初学到精通
数组 1. 前言2. 一维数组的创建和初始化3. 一维数组的使用4. 一维数组在内存中的存储5. 二维数组的创建和初始化6. 二维数组的使用7. 二维数组在内存中的存储8. 数组越界9. 数组作为函数参数10. 综合练习10.1 用函数初始化,逆置,打印整型数组10.2 交换两…...
2024-02-28(Kafka,Oozie,Flink)
1.Kafka的数据存储形式 一个主题由多个分区组成 一个分区由多个segment段组成 一个segment段由多个文件组成(log,index(稀疏索引),timeindex(根据时间做的索引)) 2.读数据的流程 …...

Window下编写的sh文件在Linux/Docker中无法使用
Window下编写的sh文件在Linux/Docker中无法使用 一、sh文件目的1.1 初始状态1.2 目的 二、过程与异常2.1 首先获取标准ubuntu20.04 - 正常2.2 启动ubuntu20.04容器 - 正常2.3 执行windows下写的preInstall文件 - 报错 三、检查和处理3.1 评估异常3.2 处理异常3.3 调整后运行测试…...
第16章-DNS
目录 1. 域名 1.1 产生背景 1.2 概述 1.3 域名的树形层次化结构 2. DNS 2.1 概述 2.2 工作机制 3. DNS查询模式 3.1 递归查询: 3.2 迭代查询: 4. 相关知识点 4.1 集中式DNS 4.2 国内通用DNS 4.3 配置DNS代理 1. 域名 1.1 产生背景 ① IP…...
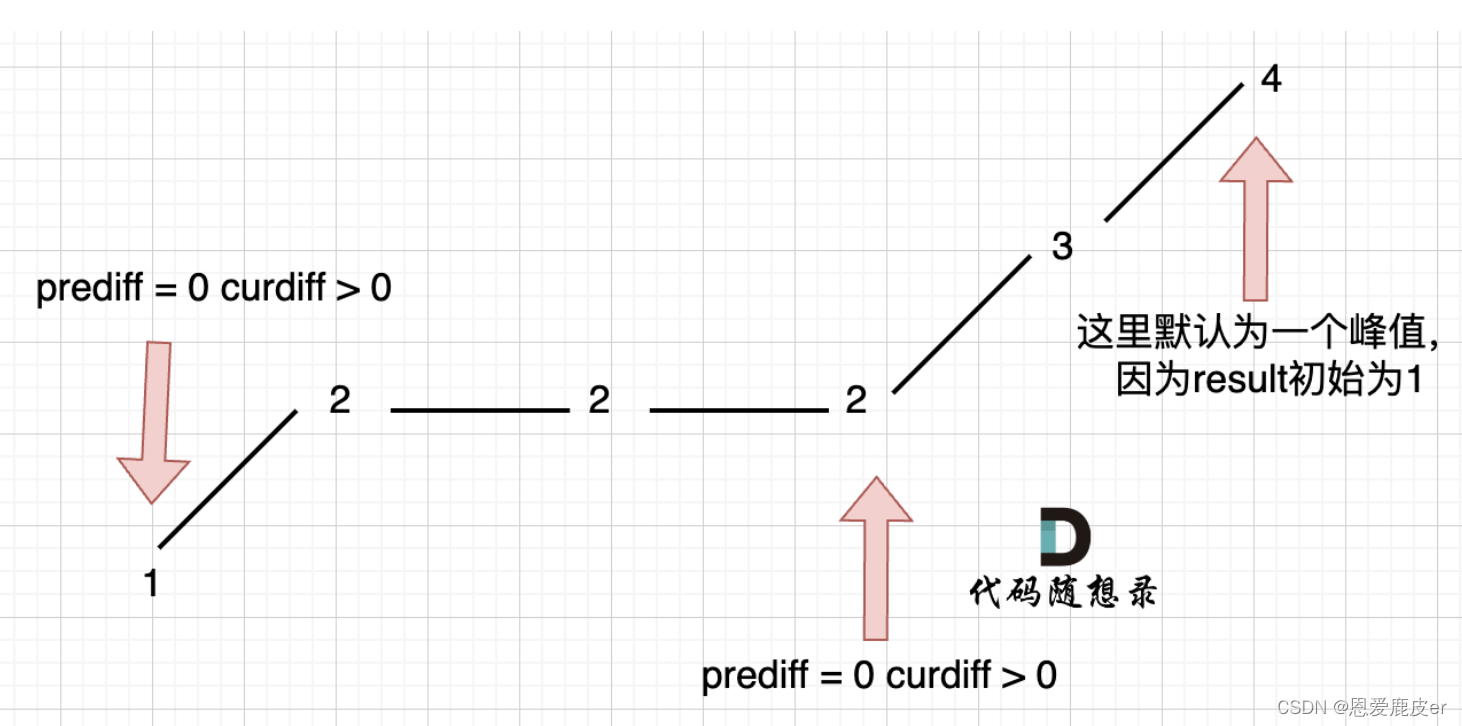
Leetcoder Day27| 贪心算法part01
语言:Java/Go 理论 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 什么时候用贪心?可以用局部最优退出全局最优,并且想不到反例到情况 贪心的一般解题步骤 将问题分解为若干个子问题找出适合的贪心策略求解每一个子…...

SpringBoot自动配置中bean的加载控制
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

Linux系统运维脚本:根据菜单选择要登录到的Linux主机,方便维护多个linux服务器
目 录 一、要求 二、解决方案 (一)解决思路 (二)方案 三、脚本程序实现 (一)脚本代码和解释 1、定义hosts.txt文件 2、脚本代码 3、代码解释 (二)脚本验证 1…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
