排序算法——快速排序的非递归写法
快速排序的非递归
我们写快速排序的时候,通常用的递归的方法实现快速排序,那么有没有非递归的方法实现快速排序呢?肯定是有的。思想还是一样的,不过非递归是看似是非递归其实还是递归。
思路解释
快速排序的非递归使用的是栈这个数据结构。我们知道栈是后入先出和先入后出的,所以我们可以通过栈的方式模拟递归,然后实现快速排序的非递归。

如图所示,创建一个栈。然后首先先将数组的起始和末尾的下标存进栈中,然后让left=begin,right=end,并pop出去。然后进行一次快排找到keyi。此时如果keyi两边的区间(绿色的)存在,就把keyi也存进栈。然后进行一次快排,当区间为空或者区间值有序,就把值从栈中pop出来,如果不是,就继续push进去,直到栈为空。最后别忘了把栈给销毁。
代码
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}
int PSort(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[key] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[key], &a[prev]);key = prev;return key;
}
void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PSort(a, left, right);// [left, keyi-1] keyi [keyi+1, right]if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}}STDestroy(&s);
}
下面是栈的头文件和.c文件
#include <stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef struct Stack
{int* a;int top; // 标识栈顶位置的int capacity;
}ST;
void STInit(ST* pst);//初始化栈
void STDestroy(ST* pst);//栈的销毁
void STPush(ST* pst, int x);//栈顶插入
void STPop(ST* pst);//栈顶删除
int STTop(ST* pst);//获取栈顶元素
bool STEmpty(ST* pst);//检查栈是否为空
int STSize(ST* pst);//获取栈中元素的个数#include "stack.h"
void STInit(ST* pst)
{/*ST* tmp = (ST*)malloc(sizeof(ST));if (tmp == NULL){perror("malloc");return;}*/pst->a = NULL;pst->top = -1;pst->capacity = 0;
}
void STPush(ST* pst, int x)
{assert(pst);if (pst->top == pst->capacity - 1){int newcapacite = pst->capacity == 0 ? 4 : pst->capacity * 2;int* tmp = (int*)realloc(pst->a, newcapacite * sizeof(int));if (tmp == NULL){perror("realloc");return;}pst->a = tmp;pst->capacity = newcapacite;}pst->a[pst->top + 1] = x;pst->top++;
}
void STPop(ST* pst)
{assert(pst);pst->top--;
}
int STTop(ST* pst)
{assert(pst);if (pst->top == -1){printf("此栈为空");return 1;}return pst->a[pst->top];
}
bool STEmpty(ST* pst)
{assert(pst);return pst->top == -1;
}
int STSize(ST* pst)
{assert(pst);return pst->top++;
}
void STDestroy(ST* pst)
{assert(pst);free(pst->a);pst->a = NULL;pst->capacity = 0;pst->top = -1;}相关文章:

排序算法——快速排序的非递归写法
快速排序的非递归 我们写快速排序的时候,通常用的递归的方法实现快速排序,那么有没有非递归的方法实现快速排序呢?肯定是有的。思想还是一样的,不过非递归是看似是非递归其实还是递归。 思路解释 快速排序的非递归使用的是栈这…...
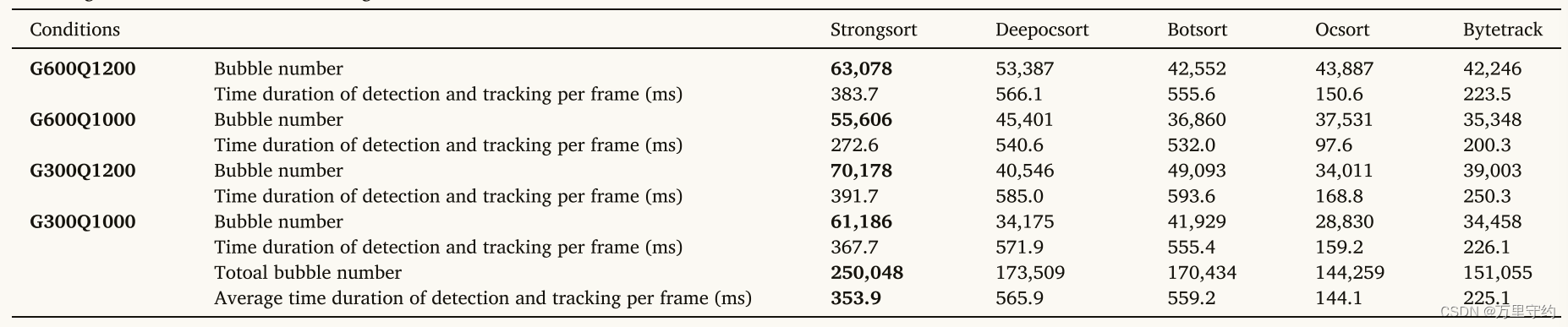
【论文阅读】基于人工智能目标检测与跟踪技术的过冷流沸腾气泡特征提取
Bubble feature extraction in subcooled flow boiling using AI-based object detection and tracking techniques 基于人工智能目标检测与跟踪技术的过冷流沸腾气泡特征提取 期刊信息:International Journal of Heat and Mass Transfer 2024 级别:EI检…...
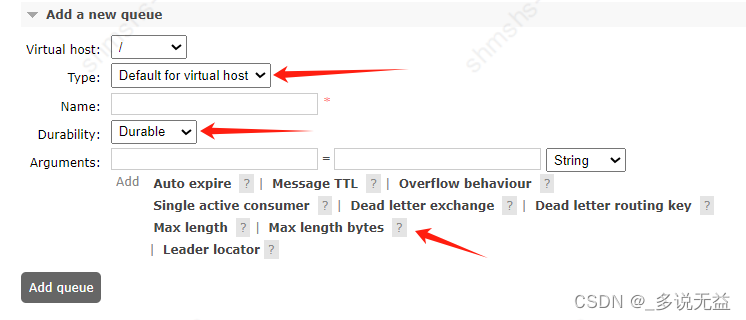
RabbitMQ讲解与整合
RabbitMq安装 类型概念 租户 RabbitMQ 中有一个概念叫做多租户,每一个 RabbitMQ 服务器都能创建出许多虚拟的消息服务器,这些虚拟的消息服务器就是我们所说的虚拟主机(virtual host),一般简称为 vhost。 每一个 vhos…...

python 基础知识点(蓝桥杯python科目个人复习计划56)
今日复习内容:做题 例题1:最小的或运算 问题描述:给定整数a,b,求最小的整数x,满足a|x b|x,其中|表示或运算。 输入格式: 第一行包括两个正整数a,b; 输出格式&#…...

【vue】vue中数据双向绑定原理/响应式原理,mvvm,mvc、mvp分别是什么
关于 vue 的原理主要有两个重要内容,分别是 mvvm 数据双向绑定原理,和 响应式原理 MVC(Model-View-Controller): Model(模型):表示应用程序的数据和业务逻辑。View(视图&…...
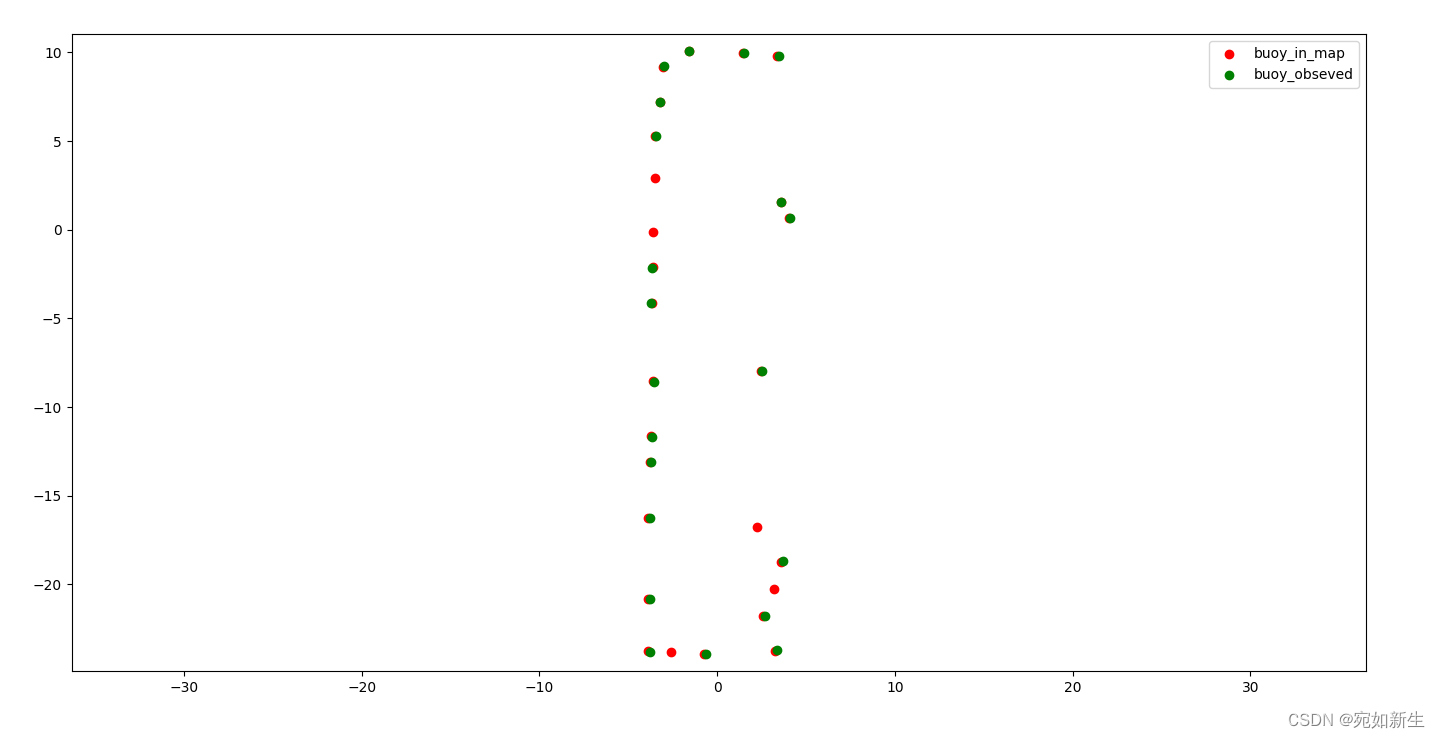
基于反光柱特征的激光定位算法思路
目录 1. 识别反光柱2. 数据关联2.1 基于几何形状寻找匹配2.2 暴力寻找匹配 3. 位姿估计(最小二乘求解)4. 问题4.1 精度问题4.2 快速旋转时定位较差 1. 识别反光柱 反光柱是特殊材料制成,根据激光雷达对反光材料扫描得到的反射值来提取特征。…...

CSM是什么意思?
CSM(Customer Service Management)是企业客户服务管理的信息化(IT)解决方案架构。本着以客户为中心的管理理念,搭建企业客户服务管理平台,实现企业以客户为中心的管理时代的竞争战略。 CSM的核心是以客户为中心,实现对…...

ES6 面试题
1. const、let 和 var 的区别是什么? 答案: var 声明的变量是函数作用域或全局作用域,而 const 和 let 声明的变量是块级作用域。使用 var 声明的变量可以被重复声明,而 const 和 let 不允许重复声明同一变量。const 声明的变量…...
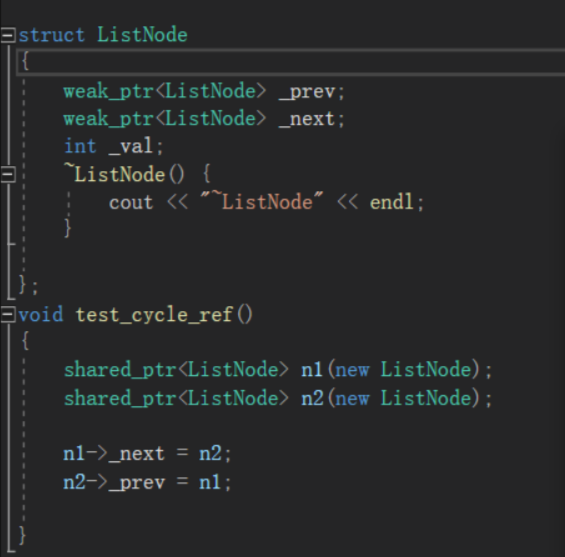
智能指针(C++)
目录 一、智能指针是什么 二、为什么需要智能指针 三、智能指针的使用和原理 3.1、RALL 3.2 智能指针的原理 3.3、智能指针的分类 3.3.1、auto_ptr 3.3.2、unique_ptr 3.3.3、shared_ptr 3.2.4、weak_ptr 一、智能指针是什么 在c中,动态内存的管理式通过一…...

社区店商业模式探讨:如何创新并持续盈利?
在竞争激烈的商业环境中,社区店要想获得成功并持续盈利,需要不断创新和优化商业模式。 作为一名开鲜奶吧5年的创业者,我将分享一些关于社区店商业模式创新的干货和见解,希望能给想开实体店或创业的朋友们提供有价值的参考。 1、…...
一些可以访问gpt的方式
1、Coze扣子是新一代 AI 大模型智能体开发平台。整合了插件、长短期记忆、工作流、卡片等丰富能力,扣子能帮你低门槛、快速搭建个性化或具备商业价值的智能体,并发布到豆包、飞书等各个平台。https://www.coze.cn/ 2、https://poe.com/ 3、插件阿里…...

springer模板参考文献不显示
Spring期刊模板网站,我的问题是23年12月的版本 https://www.springernature.com/gp/authors/campaigns/latex-author-support/see-where-our-services-will-take-you/18782940 参考文献显示问好,在sn-article.tex文件中,这个sn-mathphys-num…...
【【C语言简单小题学习-1】】
实现九九乘法表 // 输出乘法口诀表 int main() {int i 0;int j 0;for (i 1; i < 9; i){for (j 1; j < i;j)printf("%d*%d%d ", i , j, i*j);printf("\n"); }return 0; }猜数字的游戏设计 #define _CRT_SECURE_NO_WARNINGS 1 #include<stdi…...

mongoDB 优化(1)索引
1、创建复合索引(多字段) db.collection_test1.createIndex({deletedVersion: 1,param: 1,qrYearMonth: 1},{name: "deletedVersion_1_param_1_qrYearMonth_1",background: true} ); 2、新增索引前: 执行查询: mb.r…...
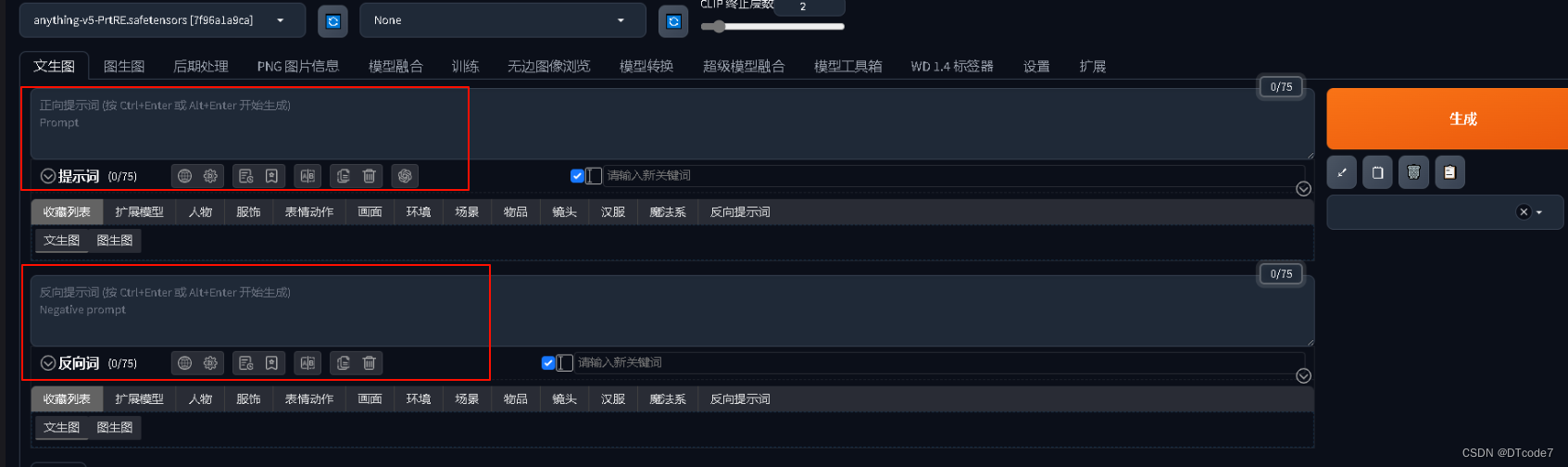
stable diffusion webUI之赛博菩萨【秋葉】——工具包新手安裝与使用教程
stable diffusion webUI之赛博菩萨【秋葉】——工具包新手安裝与使用教程 AI浪潮袭来,还是学习学习为妙赛博菩萨【秋葉】简介——(葉ye,四声,同叶)A绘世启动器.exe(sd-webui-aki-v4.6.x)工具包安…...

鸿蒙应用程序包安装和卸载流程
开发者 开发者可以通过调试命令进行应用的安装和卸载,可参考多HAP的调试流程。 图1 应用程序包安装和卸载流程(开发者) 多HAP的开发调试与发布部署流程 多HAP的开发调试与发布部署流程如下图所示。 图1 多HAP的开发调试与发布部署流程 …...

C语言数组全面解析:从初学到精通
数组 1. 前言2. 一维数组的创建和初始化3. 一维数组的使用4. 一维数组在内存中的存储5. 二维数组的创建和初始化6. 二维数组的使用7. 二维数组在内存中的存储8. 数组越界9. 数组作为函数参数10. 综合练习10.1 用函数初始化,逆置,打印整型数组10.2 交换两…...
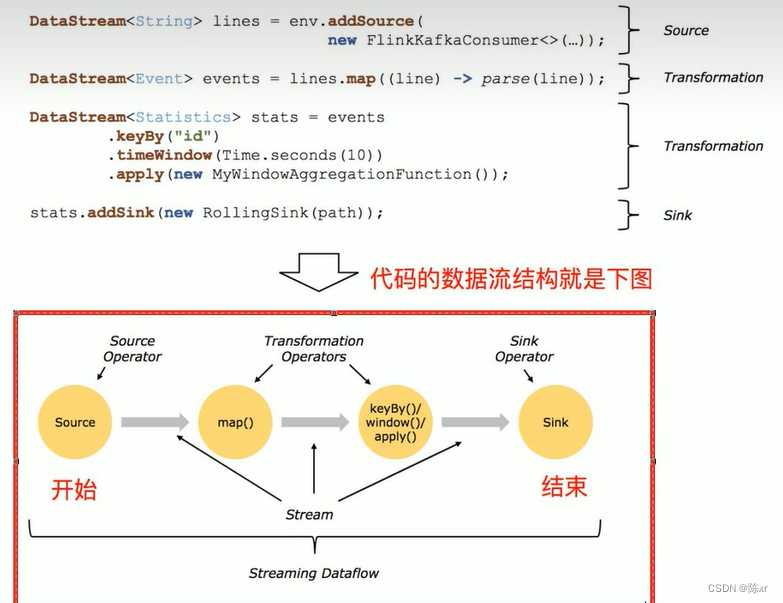
2024-02-28(Kafka,Oozie,Flink)
1.Kafka的数据存储形式 一个主题由多个分区组成 一个分区由多个segment段组成 一个segment段由多个文件组成(log,index(稀疏索引),timeindex(根据时间做的索引)) 2.读数据的流程 …...

Window下编写的sh文件在Linux/Docker中无法使用
Window下编写的sh文件在Linux/Docker中无法使用 一、sh文件目的1.1 初始状态1.2 目的 二、过程与异常2.1 首先获取标准ubuntu20.04 - 正常2.2 启动ubuntu20.04容器 - 正常2.3 执行windows下写的preInstall文件 - 报错 三、检查和处理3.1 评估异常3.2 处理异常3.3 调整后运行测试…...
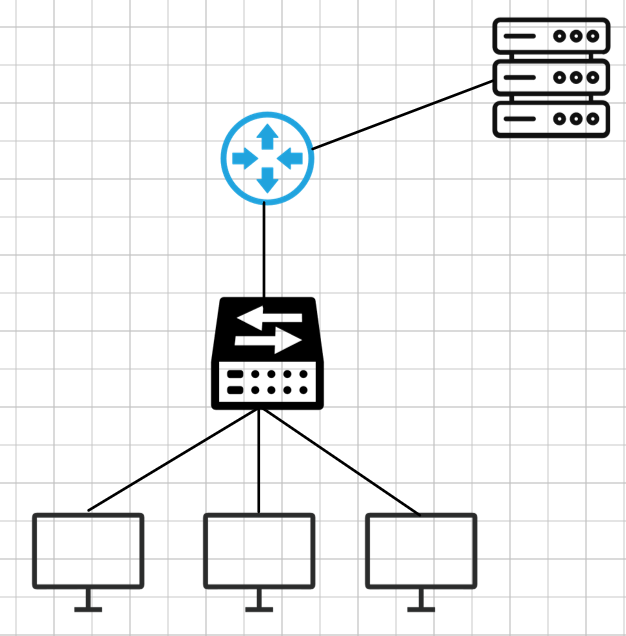
第16章-DNS
目录 1. 域名 1.1 产生背景 1.2 概述 1.3 域名的树形层次化结构 2. DNS 2.1 概述 2.2 工作机制 3. DNS查询模式 3.1 递归查询: 3.2 迭代查询: 4. 相关知识点 4.1 集中式DNS 4.2 国内通用DNS 4.3 配置DNS代理 1. 域名 1.1 产生背景 ① IP…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
