力扣 第 125 场双周赛 解题报告 | 珂学家 | 树形DP + 组合数学
前言

整体评价
T4感觉有简单的方法,无奈树形DP一条路上走到黑了,这场还是有难度的。
T1. 超过阈值的最少操作数 I
思路: 模拟
class Solution {public int minOperations(int[] nums, int k) {return (int)Arrays.stream(nums).filter(x -> x < k).count();}
}
T2. 超过阈值的最少操作数 II
思路: 模拟
按题意模拟即可,需要注意int溢出问题就行。
class Solution {public int minOperations(int[] nums, int k) {PriorityQueue<Long> pq = new PriorityQueue<>();for (long num : nums) {pq.offer(num);}int ans = 0;while (pq.peek() < k) {long x = pq.poll(), y = pq.poll();pq.offer(Math.min(x, y) * 2 + Math.max(x, y));ans++;}return ans;}
}
T3. 在带权树网络中统计可连接服务器对数目
思路: 枚举 + dfs/bfs + 组合数学
因为树的点数n( n ≤ 1000 n\le1000 n≤1000), 所以枚举点,从该点进行dfs/bfs,然后对每个分支进行组合统计。
组合统计的核心
点 u 出发的各个分支满足整除的数,组合序列为 c 0 , c 1 , c 2 , c 3 , . . . , c m 点u出发的各个分支满足整除的数,组合序列为 c_0, c_1, c_2, c_3, ..., c_m 点u出发的各个分支满足整除的数,组合序列为c0,c1,c2,c3,...,cm
其 s = ∑ i = 0 i = m c i 其 s = \sum_{i=0}^{i=m} c_i 其s=i=0∑i=mci
结果为 r e s [ u ] = ( ∑ i = 0 i = m c i ∗ ( s − c i ) ) / 2 结果为 res[u] = (\sum_{i=0}^{i=m} c_i * (s - c_i)) / 2 结果为res[u]=(i=0∑i=mci∗(s−ci))/2
这样时间复杂度为 O ( n 2 ) O(n^2) O(n2), 是可以接受的。
class Solution {List<int[]> []g;int signalSpeed;// fa是阻断点int bfs(int u, int w, int fa) {int res = 0;boolean[] vis = new boolean[g.length];Deque<int[]> deq = new ArrayDeque<>();vis[u] = true;deq.offer(new int[] {u, w});if (w % signalSpeed == 0) {res ++;}while (!deq.isEmpty()) {int[] cur = deq.poll();int p = cur[0];int v = cur[1];for (int[] e: g[p]) {if (e[0] == fa) continue;if (vis[e[0]]) continue;if ((v + e[1]) % signalSpeed == 0) res++;deq.offer(new int[] {e[0], v + e[1]});vis[e[0]] = true;}}return res;}public int[] countPairsOfConnectableServers(int[][] edges, int signalSpeed) {int n = edges.length + 1;g = new List[n];Arrays.setAll(g, x->new ArrayList<>());this.signalSpeed = signalSpeed;for (int[] e: edges) {g[e[0]].add(new int[] {e[1], e[2]});g[e[1]].add(new int[] {e[0], e[2]});}int[] res = new int[n];for (int i = 0; i < n; i++) {int sum = 0;List<Integer> lists = new ArrayList<>();for (int[] e: g[i]) {int tmp = bfs(e[0], e[1], i);lists.add(tmp);sum += tmp;}int tot = 0;for (int j = 0; j < lists.size(); j++) {tot += lists.get(j) * (sum - lists.get(j));}res[i] = tot / 2;}return res;}}
如果该题把n变成 n ≤ 1 0 5 n\le10^5 n≤105, 那该如何解呢?
感觉换根 D P 可行,但是需要限制 s i g n a l S p e e d 范围在 100 之内 , 这样可控制在 O ( 1 0 7 ) 感觉换根DP可行,但是需要限制 signalSpeed 范围在100之内, 这样可控制在O(10^7) 感觉换根DP可行,但是需要限制signalSpeed范围在100之内,这样可控制在O(107)
如果signalSpeed很大,感觉没辙啊。
T4. 最大节点价值之和
思路: 树形DP
树形DP的解法更加具有通用性,所以比赛就沿着这个思路写。
如果操作不是异或,那这个思路就更有意义 如果操作不是异或,那这个思路就更有意义 如果操作不是异或,那这个思路就更有意义
对于任意点u, 其具备两个状态。
d p [ u ] [ 0 ] , d p [ u ] [ 1 ] , 表示参与和没有参与异或下的以 u 为根节点的子树最大和。 dp[u][0], dp[u][1], 表示参与和没有参与异或下的以u为根节点的子树最大和。 dp[u][0],dp[u][1],表示参与和没有参与异或下的以u为根节点的子树最大和。
那么其转移方程,其体现在当前节点u和其子节点集合S( v ∈ u 的子节点 v\in u的子节点 v∈u的子节点)的迭代递推转移。
class Solution {int k;int[] nums;List<Integer>[]g;long[][] dp;void dfs(int u, int fa) {// 该节点没参与, 该节点参与了long r0 = nums[u], r1 = Long.MIN_VALUE / 10;for (int v: g[u]) {if (v == fa) continue;dfs(v, u);long uRev0 = r0 + (nums[u]^k) - nums[u];long uRev1 = r1 - (nums[u]^k) + nums[u];long vRev0 = dp[v][0] + (nums[v]^k) - nums[v];long vRev1 = dp[v][1] - (nums[v]^k) + nums[v];long x0 = Math.max(r0 + Math.max(dp[v][0], dp[v][1]),Math.max(uRev1 + vRev1, uRev1 + vRev0));long x1 = Math.max(r1 + Math.max(dp[v][1], dp[v][0]),Math.max(uRev0 + vRev0, uRev0 + vRev1));r0 = x0;r1 = x1;}dp[u][0] = r0;dp[u][1] = r1;}public long maximumValueSum(int[] nums, int k, int[][] edges) {int n = nums.length;this.g = new List[n];this.nums = nums;this.k = k;this.dp = new long[n][2];Arrays.setAll(g, x -> new ArrayList<>());for (int[] e: edges) {g[e[0]].add(e[1]);g[e[1]].add(e[0]);}dfs(0, -1);return Math.max(dp[0][0], dp[0][1]);}
}
class Solution:def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:n = len(nums)g = [[] for _ in range(n)]for e in edges:g[e[0]].append(e[1])g[e[1]].append(e[0])dp = [[0] * 2 for _ in range(n)]def dfs(u, fa):r0, r1 = nums[u], -0x3f3f3f3f3ffor v in g[u]:if v == fa:continuedfs(v, u)uRev0 = r0 + (nums[u]^k) - nums[u];uRev1 = r1 - (nums[u]^k) + nums[u];vRev0 = dp[v][0] + (nums[v]^k) - nums[v];vRev1 = dp[v][1] - (nums[v]^k) + nums[v];t0 = max(r0 + max(dp[v][0], dp[v][1]), max(uRev1 + vRev0, uRev1 + vRev1))t1 = max(r1 + max(dp[v][0], dp[v][1]), max(uRev0 + vRev0, uRev0 + vRev1))r0, r1 = t0, t1dp[u][0], dp[u][1] = r0, r1dfs(0, -1)return max(dp[0][0], dp[0][1])
由于异或的特点,所以这题可以抛弃边的束缚。
任意两点 u , v ,可以简单构造一条路径,只有端点 ( u , v ) 出现 1 次,其他点都出现 2 次 任意两点u,v,可以简单构造一条路径,只有端点(u,v)出现1次,其他点都出现2次 任意两点u,v,可以简单构造一条路径,只有端点(u,v)出现1次,其他点都出现2次
异或涉及边的两点,因此异或的点必然是偶数个,这是唯一的限制.
class Solution {public long maximumValueSum(int[] nums, int k, int[][] edges) {long sum = 0;PriorityQueue<Long> pq = new PriorityQueue<>(Comparator.comparing(x -> -x));for (int v: nums) {pq.offer((long)(v ^ k) - v);sum += v;}while (pq.size() >= 2) {long t1 = pq.poll();long t2 = pq.poll();if (t1 + t2 > 0) {sum += t1 + t2;} else {break;}}return sum;}
}
class Solution:def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:s = sum(nums)arr = [(v ^ k) - v for v in nums]arr.sort(key=lambda x: -x)n = len(nums)for i in range(0, n, 2):if i + 1 < n and arr[i] + arr[i + 1] > 0:s += arr[i] + arr[i + 1]return s
写在最后

相关文章:

力扣 第 125 场双周赛 解题报告 | 珂学家 | 树形DP + 组合数学
前言 整体评价 T4感觉有简单的方法,无奈树形DP一条路上走到黑了,这场还是有难度的。 T1. 超过阈值的最少操作数 I 思路: 模拟 class Solution {public int minOperations(int[] nums, int k) {return (int)Arrays.stream(nums).filter(x -> x <…...
基于springboot+vue的人格障碍诊断系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

Go-知识struct
Go-知识struct 1. struct 的定义1.1 定义字段1.2 定义方法 2. struct的复用3. 方法受体4. 字段标签4.1 Tag是Struct的一部分4.2 Tag 的约定4.3 Tag 的获取 githupio地址:https://a18792721831.github.io/ 1. struct 的定义 Go 语言的struct与Java中的class类似&am…...

SpringMVC 学习(十一)之数据校验
目录 1 数据校验介绍 2 普通校验 3 分组校验 4 参考文档 1 数据校验介绍 在实际的项目中,一般会有两种校验数据的方式:客户端校验和服务端校验 客户端校验:这种校验一般是在前端页面使用 JS 代码进行校验,主要是验证输入数据…...

软考55-上午题-【数据库】-数据库设计步骤1
一、数据库设计的步骤 新奥尔良法,四个主要阶段: 1、用户需求分析:手机用户需求,确定系统边界; 2、概念设计(概念结构设计):是抽象概念模型,较理想的是采用E-R方法。 …...

速盾:使用cdn后速度慢是怎么回事?
CDN(内容分发网络)是一种通过将网站的静态内容分布到全球各地的服务器,从而提供更快速度和更好用户体验的技术。然而,有时候用户会遇到使用CDN后速度变慢的问题,下面将探讨几种可能的原因。 服务器选择错误: CDN服务通…...
考研复试类比社团招新,无所谓“公平”,导师选谁都是他的权力
这篇文章是抖音和b站上上传的同名视频的原文稿件,感兴趣的csdn用户可以关注我的抖音和b站账号(GeekPower极客力量)。同时这篇文章也为视频观众提供方便,可以更加冷静地分析和思考。文章同时在知乎发表。 我考研一战的时候计算机考…...

阿里面试,有点焦虑。。
恭喜发现宝藏!搜索公众号【TechGuide】回复公司名,解锁更多新鲜好文和互联网大厂的笔经面经,目前已更新至美团、字节… 作者TechGuide【全网同名】 聊聊春招 春招来了,有些24届校招生可能还在做最后的努力,有些25届的…...

24计算机考研调剂 | 石家庄铁道大学
01石家庄铁道大学 智慧交通研究室招少量调剂学术型硕士(数一英一320分以上工科专业) 考研调剂招生信息 学校:石家庄铁道大学 专业:工学->计算机科学与技术->计算机应用技术 工学->测绘科学与技术->地图制图学与地理信息工程 工学->交…...

勇敢尝鲜之Springboot3大坑-集成Mybatisplus报错:ddlApplicationRunner
🌹作者主页:青花锁 🌹简介:Java领域优质创作者🏆、Java微服务架构公号作者😄 🌹简历模板、学习资料、面试题库、技术互助 🌹文末获取联系方式 📝 往期热门专栏回顾 专栏…...
linux高级编程:线程(二)、进程间的通信方式
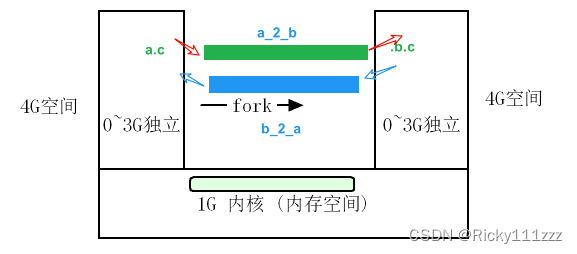
线程: 回顾线程(一): 1.线程间通信问题 线程间共享同一个资源(临界资源) 互斥: 排他性访问 linux系统 -- 提供了Posix标准的函数库 -- 互斥量(互斥锁) 原子操作&#x…...

Unity 佳能SDK 及数据获取
1. 填写信息跟官方申请SDK,大概1-2个工作日会邮件回复你 佳能(中国)- 佳定制(佳能影像产品),SDK,EDSDK,CCAPI,软件开发包下载 2. 将SDK这两个文件放到 Unity Plugins文件夹 3. 把CameraControl 下面只要是绿色的 .cs 文件都复制到Unity 中...
Unity(第二十三部)导航
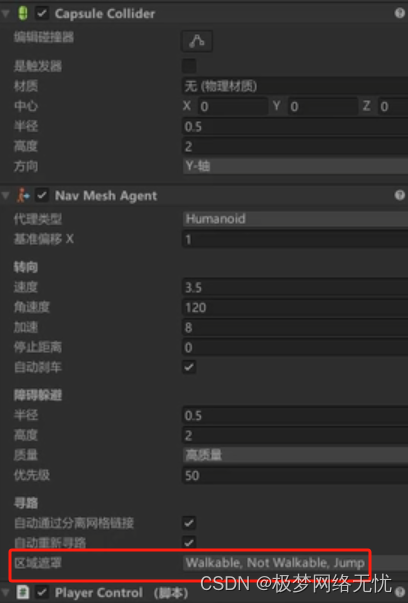
你可以使用 unity官方提供的 unity导航组件或第三方 unity导航组件,以实现游戏中角色或其他物体的导航。 unity导航组件通常具有多种导航模式,如飞行模式、步行模式、车辆模式等,可以根据不同的需求选择合适的模式。同时,unity导…...

根据建表sql语句生成go的struct代码工具
sql2struct 一个根据"CREATE TABLE"建表语句生成对应的Go语言结构体的工具,暂只支持 MySQL 表。 开发目的 在 github 中找到一些 sql2struct,但要么是 chrome 插件,要么是在线工具,要么是需要连接 MySQL,…...
Qt 自定义长条进度条(类似播放器进度条)
1.运行界面 2.步骤 其实很简单。 2.1绘制底图圆角矩形 2.2绘制播放进度圆角矩形 参考:painter绘图 3.源码 #pragma once#include <QWidget> #include <QLabel> #include <QHBoxLayout> #include <QMouseEvent> #include <QDebug&g…...

休息日的思考与额外题——双指针、原地哈希day28
文章目录 前言一、11. 盛最多水的容器二、41. 缺失的第一个正数三、42. 接雨水总结 前言 一个本硕双非的小菜鸡,备战24年秋招,计划二刷完卡子哥的刷题计划,加油! 二刷决定精刷了,于是参加了卡子哥的刷题班,…...

数据修改
Oracle 目录 数据修改 将员工编号的 7369 的员工工资修改为 810,佣金改为 100 将工资最低的员工工资修改为公司的平均工资 将所有在 1981 年雇佣的员工的雇佣日期修改为今天,工资增长 20% 数据的更新操作 Oracle从入门到总裁:https://blog.csdn.n…...

Android JNI复杂用法,回调,C++中调用Java方法
Android JNI复杂用法,回调,C中调用Java方法 一、前言 Android JNI的 普通用法估计很多人都会,但是C中调用Java方法很多人不熟悉,并且网上很多介绍都是片段的。 虽然C/C调用Java不常用,但是掌握多一点还是有好处的。…...
)
C++从零开始的打怪升级之路(day41)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于继承的知识点 1.派生类的默认成员函数 首先我…...

uni-app app实现web-view H5图片长按下载
问题和使用场景描述: uniapp app web-view中图片无法长按保存,IOS下是正常的,但是Android下长按无反应 解决方案: 下载mui.min.js,放到项目中的static下(下载见最上面的压缩包) 在static目录下新建script.js mui.…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
