寻找峰值[中等]
优质博文IT-BLOG-CN
一、题目
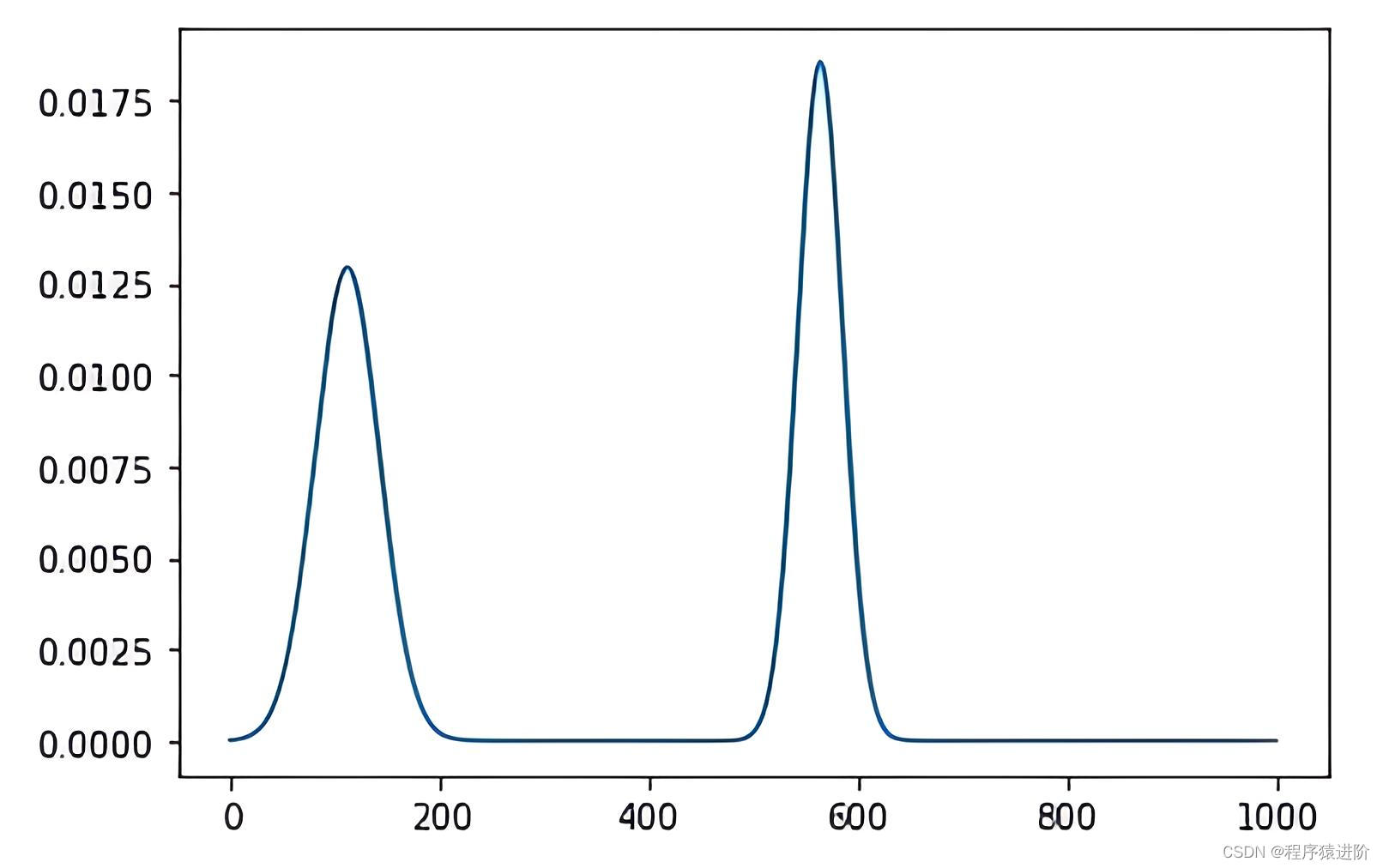
峰值元素是指其值严格大于左右相邻值的元素。给你一个整数数组nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设nums[-1] = nums[n] = -∞。
你必须实现时间复杂度为
O(log n)的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3是峰值元素,你的函数应该返回其索引2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1或5
解释:你的函数可以返回索引1,其峰值元素为2;或者返回索引5, 其峰值元素为6。
提示:
1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
对于所有有效的i都有nums[i] != nums[i + 1]
二、代码
方案一:寻找最大值
由于题目保证了nums[i]≠nums[i+1],那么数组nums中最大值两侧的元素一定严格小于最大值本身。因此,最大值所在的位置就是一个可行的峰值位置。
我们对数组nums进行一次遍历,找到最大值对应的位置即可。
class Solution {public int findPeakElement(int[] nums) {int idx = 0;for (int i = 1; i < nums.length; ++i) {if (nums[i] > nums[idx]) {idx = i;}}return idx;}
}
时间复杂度: O(n),其中n是数组nums的长度。
空间复杂度: O(1)。
方案二:二分查找
首先要注意题目条件,在题目描述中出现了nums[-1] = nums[n] = -∞,这就代表着 只要数组中存在一个元素比相邻元素大,那么沿着它一定可以找到一个峰值。
根据上述结论,我们就可以使用二分查找找到峰值
查找时,左指针l,右指针r,以其保持左右顺序为循环条件
根据左右指针计算中间位置m,并比较m与m+1的值,如果m较大,则左侧存在峰值,r = m,如果m + 1较大,则右侧存在峰值,l = m + 1
class Solution {public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;for (; left < right; ) {int mid = left + (right - left) / 2;if (nums[mid] > nums[mid + 1]) {right = mid;} else {left = mid + 1;}}return left;}
}
时间复杂度: O(logn),其中n是数组nums的长度。
空间复杂度: O(1)。
方案三:迭代爬坡
俗话说「人往高处走,水往低处流」。如果我们从一个位置开始,不断地向高处走,那么最终一定可以到达一个峰值位置。
因此,我们首先在[0,n)的范围内随机一个初始位置i,随后根据nums[i−1],nums[i],nums[i+1]三者的关系决定向哪个方向走:
【1】如果nums[i−1]<nums[i]>nums[i+1],那么位置i就是峰值位置,我们可以直接返回i作为答案;
【2】如果nums[i−1]<nums[i]<nums[i+1],那么位置i处于上坡,我们需要往右走,即i←i+1;
如果nums[i−1]>nums[i]>nums[i+1],那么位置i处于下坡,我们需要往左走,即i←i−1;
如果nums[i−1]>nums[i]<nums[i+1],那么位置i位于山谷,两侧都是上坡,我们可以朝任意方向走。
如果我们规定对于最后一种情况往右走,那么当位置i不是峰值位置时:
【1】如果nums[i]<nums[i+1],那么我们往右走;
【2】如果nums[i]>nums[i+1],那么我们往左走。
class Solution {public int findPeakElement(int[] nums) {int n = nums.length;int idx = (int) (Math.random() * n);while (!(compare(nums, idx - 1, idx) < 0 && compare(nums, idx, idx + 1) > 0)) {if (compare(nums, idx, idx + 1) < 0) {idx += 1;} else {idx -= 1;}}return idx;}// 辅助函数,输入下标 i,返回一个二元组 (0/1, nums[i])// 方便处理 nums[-1] 以及 nums[n] 的边界情况public int[] get(int[] nums, int idx) {if (idx == -1 || idx == nums.length) {return new int[]{0, 0};}return new int[]{1, nums[idx]};}public int compare(int[] nums, int idx1, int idx2) {int[] num1 = get(nums, idx1);int[] num2 = get(nums, idx2);if (num1[0] != num2[0]) {return num1[0] > num2[0] ? 1 : -1;}if (num1[1] == num2[1]) {return 0;}return num1[1] > num2[1] ? 1 : -1;}
}
时间复杂度: O(n),其中n是数组nums的长度。在最坏情况下,数组nums单调递增,并且我们随机到位置0,这样就需要向右走到数组nums的最后一个位置。
空间复杂度: O(1)。
方法四:二分查找优化
我们可以发现,如果nums[i]<nums[i+1],并且我们从位置i向右走到了位置i+1,那么位置i左侧的所有位置是不可能在后续的迭代中走到的。
这是因为我们每次向左或向右移动一个位置,要想「折返」到位置i以及其左侧的位置,我们首先需要在位置i+1向左走到位置i,但这是不可能的。
并且根据方法二,我们知道位置i+1以及其右侧的位置中一定有一个峰值,因此我们可以设计出如下的一个算法:
【1】对于当前可行的下标范围[l,r],我们随机一个下标i;
【2】如果下标i是峰值,我们返回i作为答案;
【3】如果nums[i]<nums[i+1],那么我们抛弃[l,i]的范围,在剩余[i+1,r]的范围内继续随机选取下标;
【4】如果nums[i]>nums[i+1],那么我们抛弃[i,r]的范围,在剩余[l,i−1]的范围内继续随机选取下标。
在上述算法中,如果我们固定选取i为[l,r]的中点,那么每次可行的下标范围会减少一半,成为一个类似二分查找的方法,时间复杂度为 O(logn)。
class Solution {public int findPeakElement(int[] nums) {int n = nums.length;int left = 0, right = n - 1, ans = -1;while (left <= right) {int mid = (left + right) / 2;if (compare(nums, mid - 1, mid) < 0 && compare(nums, mid, mid + 1) > 0) {ans = mid;break;}if (compare(nums, mid, mid + 1) < 0) {left = mid + 1;} else {right = mid - 1;}}return ans;}// 辅助函数,输入下标 i,返回一个二元组 (0/1, nums[i])// 方便处理 nums[-1] 以及 nums[n] 的边界情况public int[] get(int[] nums, int idx) {if (idx == -1 || idx == nums.length) {return new int[]{0, 0};}return new int[]{1, nums[idx]};}public int compare(int[] nums, int idx1, int idx2) {int[] num1 = get(nums, idx1);int[] num2 = get(nums, idx2);if (num1[0] != num2[0]) {return num1[0] > num2[0] ? 1 : -1;}if (num1[1] == num2[1]) {return 0;}return num1[1] > num2[1] ? 1 : -1;}
}
时间复杂度: O(logn),其中n是数组nums的长度。
空间复杂度: O(1)。
相关文章:

寻找峰值[中等]
优质博文IT-BLOG-CN 一、题目 峰值元素是指其值严格大于左右相邻值的元素。给你一个整数数组nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。 你可以假设nums[-1] nums[n] -∞。 你…...
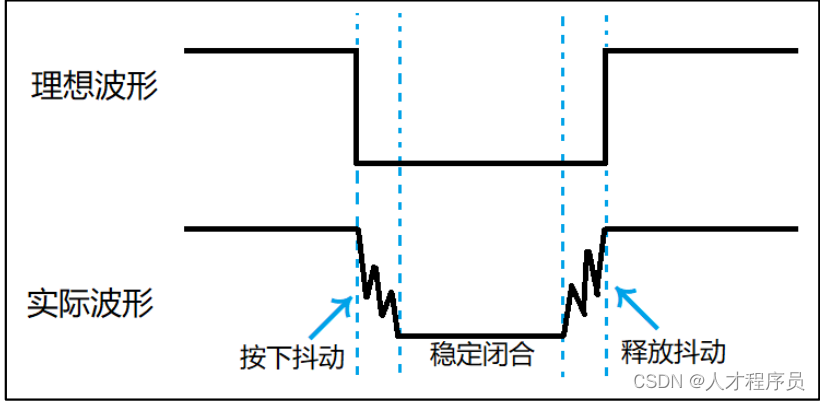
【ESP32 IDF】key按键与EXTI中断
文章目录 前言一、按键的使用1.1 按键的简介1.2 读取按键的高低电平1.3 读取按键具体代码 二、中断二、EXIT外部中断2.1 EXIT外部中断简介2.2 外部中断基础知识2.3 设置外部中断注册外部中断服务函数设置触发方式添加中断函数 2.4 示例代码 总结 前言 在嵌入式系统开发中&…...

Find My运动相机|苹果Find My技术与相机结合,智能防丢,全球定位
运动相机设计用于在各种运动和极限环境中使用,如徒步、登山、攀岩、骑行、滑翔、滑雪、游泳和潜水等,它们通常具有防抖防震、深度防水和高清画质的特点,能够适应颠簸剧烈的环境,甚至可以承受一定程度的摔落,一些运动相…...

零拷贝技术深入分析
一、零拷贝 在前面的文章“深浅拷贝、COW及零拷贝”中对零拷贝进行过分析,但没有举例子,也没有深入进行展开分析。本文将结合实际的例程对零拷贝进行更深入的分析和说明。 在传统的IO操作中,以文件通过网络传输为例 ,一般会经历以…...
Android 基础入门 基础简介
1. 观察App运行日志 2.Android 开发设计的编程语言 koltin Java c c 3.工程目录结构 4.Gradle 5.build.gradle 文件解析 plugins {id("com.android.application")//用了哪些插件 主配置文件版本控制 所以这里不用写版本 }android {namespace "com.tiger.myap…...
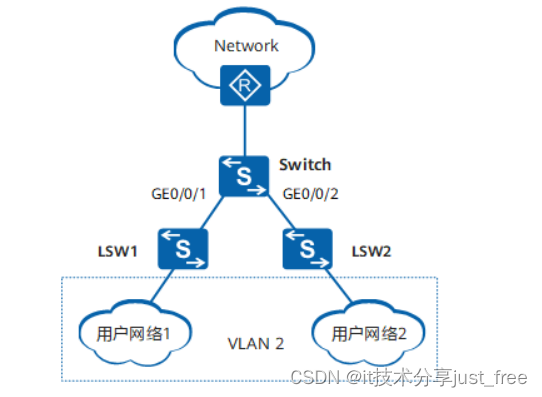
HUAWEI 华为交换机 配置基于VLAN的MAC地址学习限制接入用户数量 配置示例
组网需求 如 图 2-15 所示,用户网络 1 通过 LSW1 与 Switch 相连, Switch 的接口为 GE0/0/1 。用户网络2通过 LSW2 与 Switch 相连, Switch 的接口为 GE0/0/2 。 GE0/0/1 、 GE0/0/2 同属于 VLAN2。为控制接入用户数,对 VLAN2 进…...

编程笔记 Golang基础 042 文件处理
编程笔记 Golang基础 042 文件处理 一、文件处理二、Go语言文件处理创建文件和写入内容打开文件并按模式读写读取文件内容更高级的文件和IO操作改变文件权限目录操作 小结 一、文件处理 文件处理是指在计算机科学中,对存储在磁盘或其他持久性存储介质上的文件进行的…...

linuxlsof详解
lsof 是 List Open File 的缩写, 它主要用来获取被进程打开文件的信息,我们都知道,在Linux中,一切皆文件,lsof命令可以查看所有已经打开了的文件,比如: 普通文件,目录,特殊的块文件,…...
)
学习JAVA的第十二天(基础)
目录 算法 查找算法 基本查找(顺序查找) 二分查找(折半查找) 分块查找 排序算法 冒泡排序 选择排序 插入排序 快速排序 递归算法 算法 算法(Algorithm)是指解题方案的准确而完整的描述ÿ…...

Vector集合源码分析
Vector集合源码分析 文章目录 Vector集合源码分析一、字段分析二、方法分析三、总结 内容如有错误或者其他需要注意的知识点,欢迎指正或者探讨补充,共同进步。 一、字段分析 //用于存储该集合中的所有数据对象,所以是基于数组实现的 protec…...

Unity引擎中光源都有哪几种,都有什么作用
本文由 简悦 SimpRead 转码, 原文地址 mp.weixin.qq.com Unity 引擎为了实现游戏场景的明暗和光影效果,提供了四种类型的光源,分别是方向光(Directional Lights)、点光源(Point Lights)、聚光灯…...

C语言中结构体成员访问操作符的含义及其用法
1.直接访问操作符 用法:结构体名.成员名。 含义:直接访问结构体中的成员变量。 示例: #include<stdio.h> struct student {char name[20];int age; }; int main() {//定义了一个结构体数组arrstruct student arr[4] { {"cxk&q…...

Kubeadmin方式部署Calico网络模式的K8s集群
目录 1.环境准备 2.配置内核参数 3.配置ntp时间服务器 4.配置持久化日志目录 5.升级物理机内核 6.配置ipvs服务 7.安装docker 8.安装kubeadm、kubectl、kubelet 9.导入k8s组件基础镜像 10.k8s初始化配置 11.配置calico网络 12.完成部署 1.环境准备 ###方案中涉及的…...
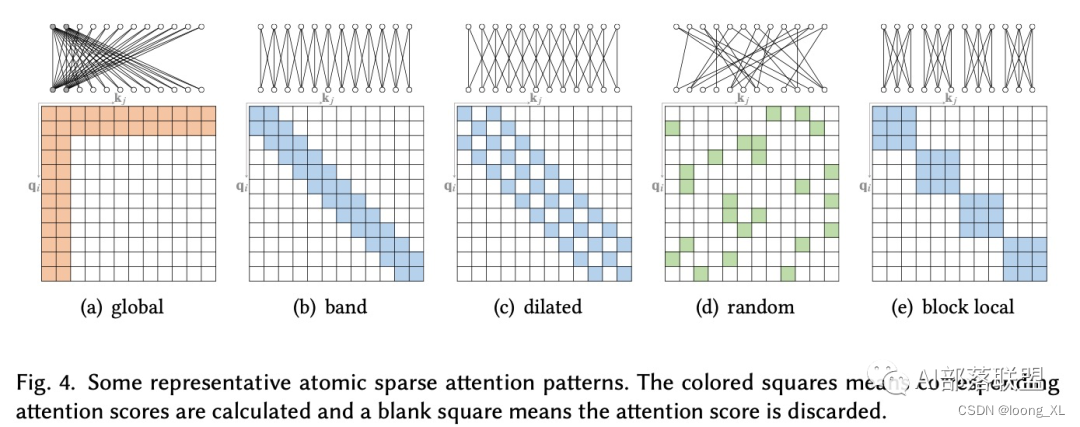
sparse transformer 常见稀疏注意力
参考: https://zhuanlan.zhihu.com/p/259591644 主要就是降低transformer自注意力模块的复杂度 复杂度主要就是 Q K^T影响的,稀疏注意力就是在Q点乘K的转置这模块做文章 下列式一些sparse transformer稀疏注意力方法 a、transformer原始的 ࿰…...

力扣 第 125 场双周赛 解题报告 | 珂学家 | 树形DP + 组合数学
前言 整体评价 T4感觉有简单的方法,无奈树形DP一条路上走到黑了,这场还是有难度的。 T1. 超过阈值的最少操作数 I 思路: 模拟 class Solution {public int minOperations(int[] nums, int k) {return (int)Arrays.stream(nums).filter(x -> x <…...
基于springboot+vue的人格障碍诊断系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

Go-知识struct
Go-知识struct 1. struct 的定义1.1 定义字段1.2 定义方法 2. struct的复用3. 方法受体4. 字段标签4.1 Tag是Struct的一部分4.2 Tag 的约定4.3 Tag 的获取 githupio地址:https://a18792721831.github.io/ 1. struct 的定义 Go 语言的struct与Java中的class类似&am…...

SpringMVC 学习(十一)之数据校验
目录 1 数据校验介绍 2 普通校验 3 分组校验 4 参考文档 1 数据校验介绍 在实际的项目中,一般会有两种校验数据的方式:客户端校验和服务端校验 客户端校验:这种校验一般是在前端页面使用 JS 代码进行校验,主要是验证输入数据…...

软考55-上午题-【数据库】-数据库设计步骤1
一、数据库设计的步骤 新奥尔良法,四个主要阶段: 1、用户需求分析:手机用户需求,确定系统边界; 2、概念设计(概念结构设计):是抽象概念模型,较理想的是采用E-R方法。 …...

速盾:使用cdn后速度慢是怎么回事?
CDN(内容分发网络)是一种通过将网站的静态内容分布到全球各地的服务器,从而提供更快速度和更好用户体验的技术。然而,有时候用户会遇到使用CDN后速度变慢的问题,下面将探讨几种可能的原因。 服务器选择错误: CDN服务通…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
