文心一言 VS 讯飞星火 VS chatgpt (207)-- 算法导论15.4 4题
四、说明如何只使用表 c 中 2*min(m,n) 个表项及O(1)的额外空间来计算LCS的长度。然后说明如何只用 min(m,n) 个表项及O(1)的额外空间完成相同的工作。要写代码的时候,请用go语言。
文心一言:
在只使用 2 * min(m, n) 个表项和 O(1) 额外空间来计算 LCS(Longest Common Subsequence)的长度时,我们可以采用滚动数组(Rolling Array)的技巧。这种方法的核心思想是在填充 DP 表时只保留前一行的数据,因为当前行的数据只依赖于前一行的数据。这样我们就可以避免存储整个二维数组,而只存储一行数组即可。
首先,我们创建一个长度为 n + 1 的数组 dp,其中 dp[j] 表示 str1 的前 i 个字符和 str2 的前 j 个字符的 LCS 长度。由于我们只需要前一行的数据,我们可以在计算新行时覆盖旧行的数据。
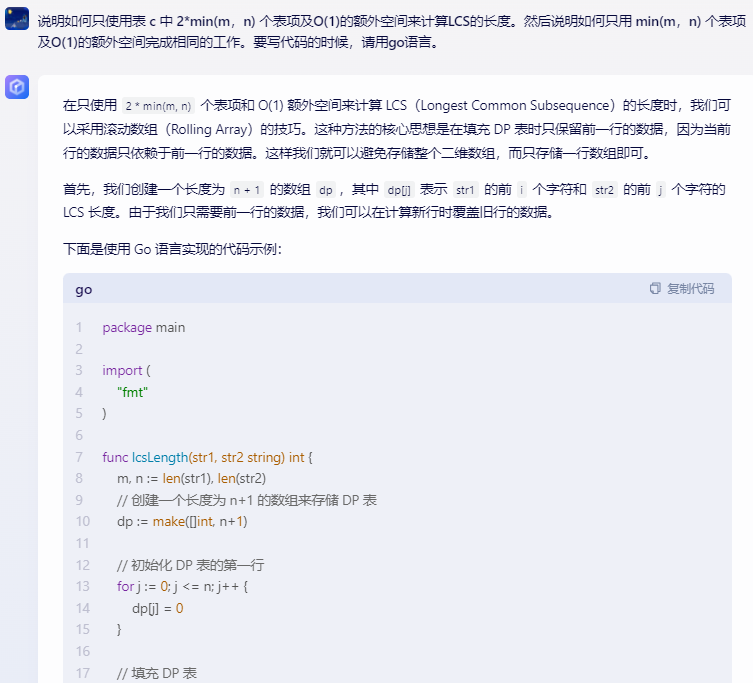
下面是使用 Go 语言实现的代码示例:
package main import ( "fmt"
) func lcsLength(str1, str2 string) int { m, n := len(str1), len(str2) // 创建一个长度为 n+1 的数组来存储 DP 表 dp := make([]int, n+1) // 初始化 DP 表的第一行 for j := 0; j <= n; j++ { dp[j] = 0 } // 填充 DP 表 for i := 1; i <= m; i++ { // 保存前一行的第一个元素,以便在更新当前行时使用 prev := dp[0] // 更新当前行 for j := 1; j <= n; j++ { curr := dp[j] if str1[i-1] == str2[j-1] { dp[j] = prev + 1 } else { dp[j] = max(dp[j], dp[j-1]) } prev = curr } } // 返回 LCS 的长度 return dp[n]
} func max(a, b int) int { if a > b { return a } return b
} func main() { str1 := "ABCDEFG" str2 := "XYZABCDEFGHIJKL" length := lcsLength(str1, str2) fmt.Printf("The length of the Longest Common Subsequence is: %d\n", length)
}
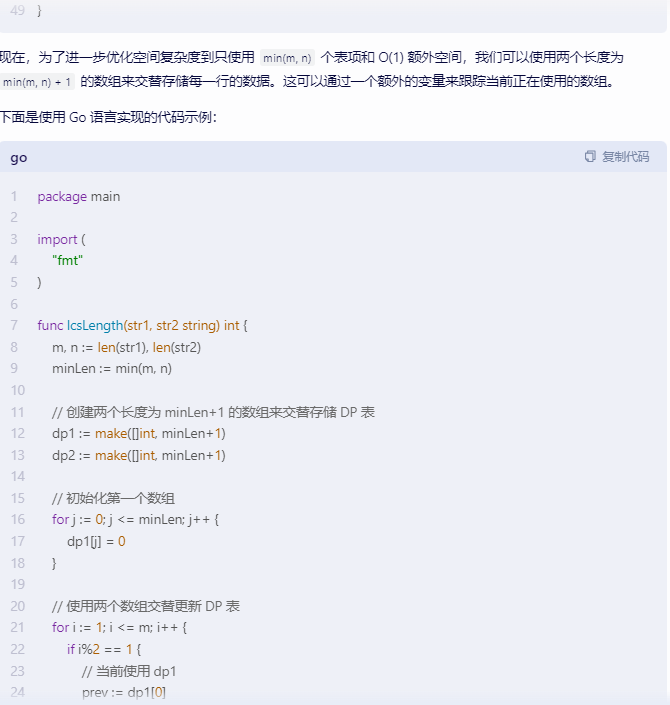
现在,为了进一步优化空间复杂度到只使用 min(m, n) 个表项和 O(1) 额外空间,我们可以使用两个长度为 min(m, n) + 1 的数组来交替存储每一行的数据。这可以通过一个额外的变量来跟踪当前正在使用的数组。
下面是使用 Go 语言实现的代码示例:
package main import ( "fmt"
) func lcsLength(str1, str2 string) int { m, n := len(str1), len(str2) minLen := min(m, n) // 创建两个长度为 minLen+1 的数组来交替存储 DP 表 dp1 := make([]int, minLen+1) dp2 := make([]int, minLen+1) // 初始化第一个数组 for j := 0; j <= minLen; j++ { dp1[j] = 0 } // 使用两个数组交替更新 DP 表 for i := 1; i <= m; i++ { if i%2 == 1 { // 当前使用 dp1 prev := dp1[0] for j := 1; j <= minLen; j++ { curr := dp1[j] if str1[i-1] == str2[j-1] { dp2[j] = prev + 1 } else { dp2[j] = max(dp1[j], dp1[j-1]) } prev = curr } // 交换数组 dp1, dp2 = dp2, dp1 } else { // 当前使用 dp2 prev := dp2[0] for j := 1; j


讯飞星火:
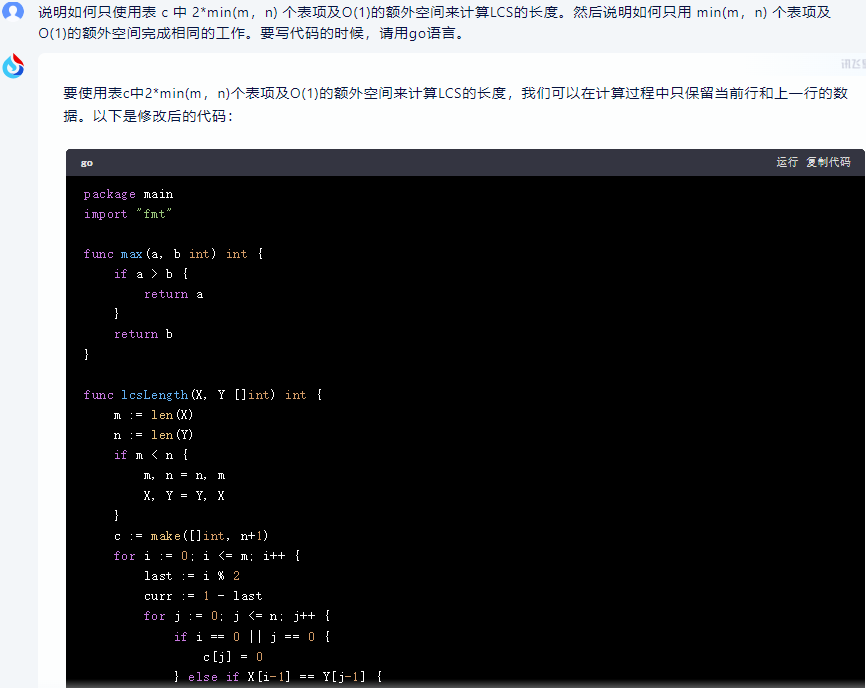
要使用表c中2*min(m,n)个表项及O(1)的额外空间来计算LCS的长度,我们可以在计算过程中只保留当前行和上一行的数据。以下是修改后的代码:
package main
import "fmt"func max(a, b int) int {if a > b {return a}return b
}func lcsLength(X, Y []int) int {m := len(X)n := len(Y)if m < n {m, n = n, mX, Y = Y, X}c := make([]int, n+1)for i := 0; i <= m; i++ {last := i % 2curr := 1 - lastfor j := 0; j <= n; j++ {if i == 0 || j == 0 {c[j] = 0} else if X[i-1] == Y[j-1] {c[j] = c[j-1] + 1} else {c[j] = max(c[j-1], c[j])}}}return c[n]
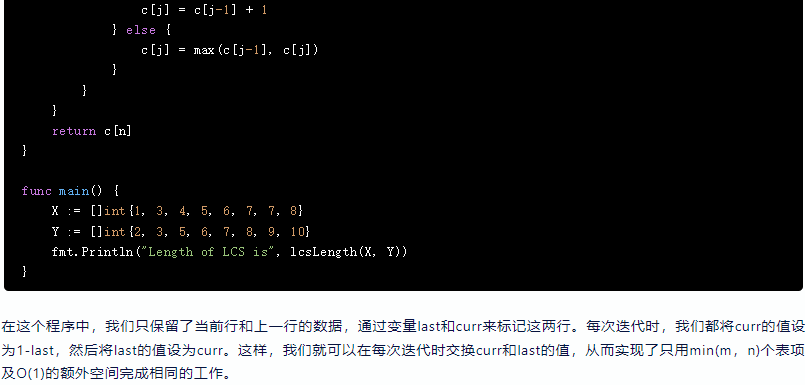
}func main() {X := []int{1, 3, 4, 5, 6, 7, 7, 8}Y := []int{2, 3, 5, 6, 7, 8, 9, 10}fmt.Println("Length of LCS is", lcsLength(X, Y))
}
在这个程序中,我们只保留了当前行和上一行的数据,通过变量last和curr来标记这两行。每次迭代时,我们都将curr的值设为1-last,然后将last的值设为curr。这样,我们就可以在每次迭代时交换curr和last的值,从而实现了只用min(m,n)个表项及O(1)的额外空间完成相同的工作。
360智脑:
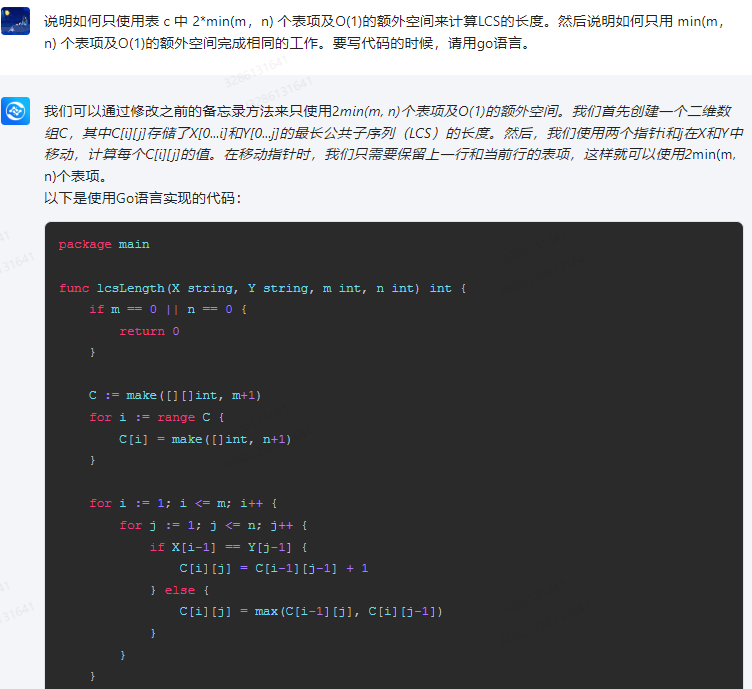
我们可以通过修改之前的备忘录方法来只使用2min(m, n)个表项及O(1)的额外空间。我们首先创建一个二维数组C,其中C[i][j]存储了X[0…i]和Y[0…j]的最长公共子序列(LCS)的长度。然后,我们使用两个指针i和j在X和Y中移动,计算每个C[i][j]的值。在移动指针时,我们只需要保留上一行和当前行的表项,这样就可以使用2min(m, n)个表项。
以下是使用Go语言实现的代码:
package main func lcsLength(X string, Y string, m int, n int) int {if m == 0 || n == 0 {return 0 }C := make([][]int, m+1)for i := range C {C[i] = make([]int, n+1)}for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if X[i-1] == Y[j-1] {C[i][j] = C[i-1][j-1] + 1 } else {C[i][j] = max(C[i-1][j], C[i][j-1])}}}return C[m][n]
}func max(a, b int) int {if a > b {return a }return b
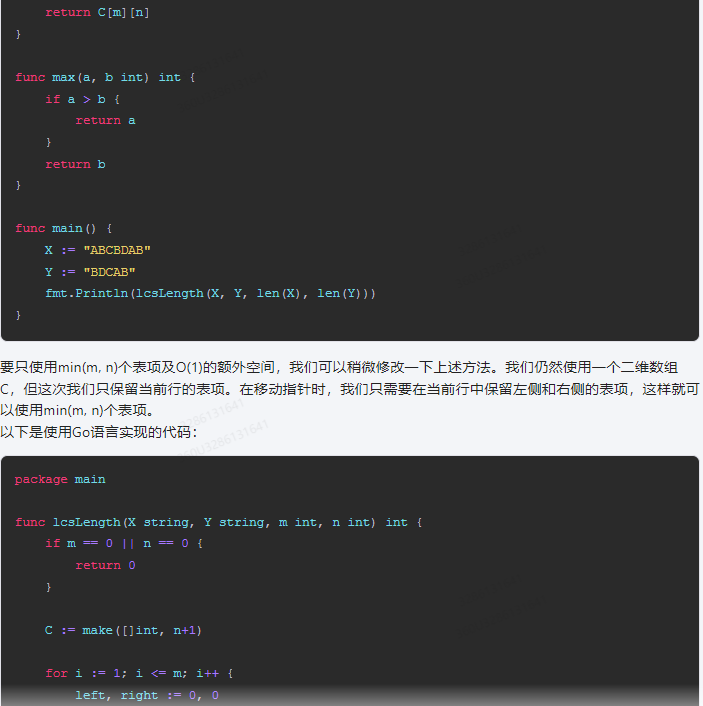
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println(lcsLength(X, Y, len(X), len(Y)))
}
要只使用min(m, n)个表项及O(1)的额外空间,我们可以稍微修改一下上述方法。我们仍然使用一个二维数组C,但这次我们只保留当前行的表项。在移动指针时,我们只需要在当前行中保留左侧和右侧的表项,这样就可以使用min(m, n)个表项。
以下是使用Go语言实现的代码:
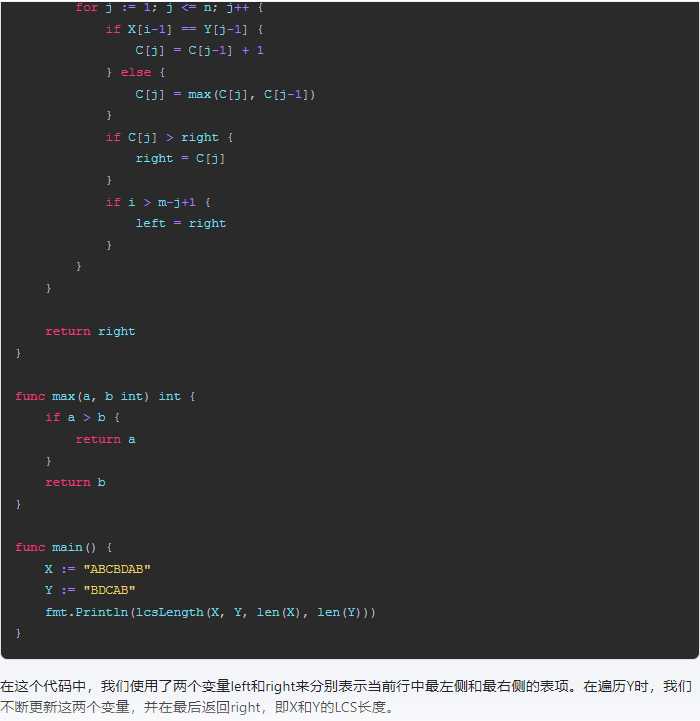
package main func lcsLength(X string, Y string, m int, n int) int {if m == 0 || n == 0 {return 0 }C := make([]int, n+1)for i := 1; i <= m; i++ {left, right := 0, 0 for j := 1; j <= n; j++ {if X[i-1] == Y[j-1] {C[j] = C[j-1] + 1 } else {C[j] = max(C[j], C[j-1])}if C[j] > right {right = C[j]}if i > m-j+1 {left = right }}}return right
}func max(a, b int) int {if a > b {return a }return b
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println(lcsLength(X, Y, len(X), len(Y)))
}
在这个代码中,我们使用了两个变量left和right来分别表示当前行中最左侧和最右侧的表项。在遍历Y时,我们不断更新这两个变量,并在最后返回right,即X和Y的LCS长度。
智谱清言:
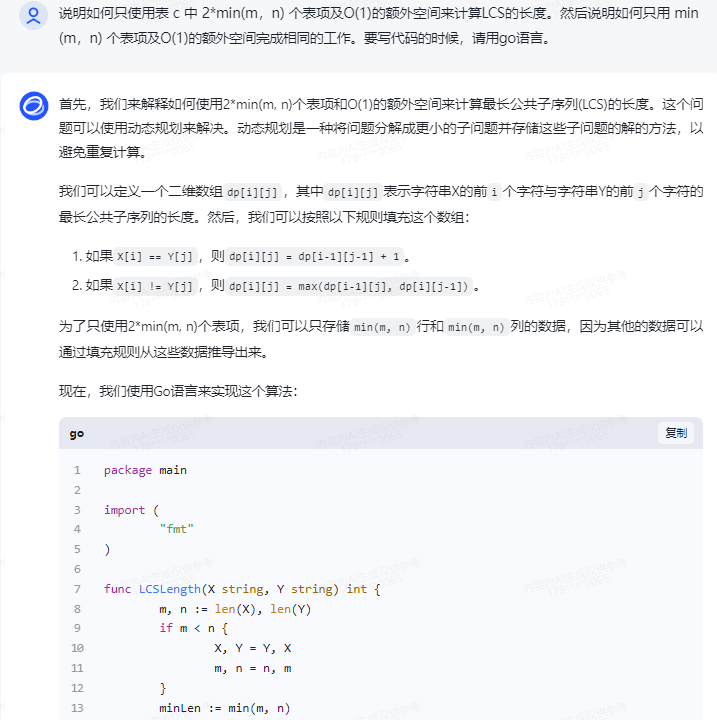
首先,我们来解释如何使用2*min(m, n)个表项和O(1)的额外空间来计算最长公共子序列(LCS)的长度。这个问题可以使用动态规划来解决。动态规划是一种将问题分解成更小的子问题并存储这些子问题的解的方法,以避免重复计算。
我们可以定义一个二维数组dp[i][j],其中dp[i][j]表示字符串X的前i个字符与字符串Y的前j个字符的最长公共子序列的长度。然后,我们可以按照以下规则填充这个数组:
1.如果X[i] == Y[j],则dp[i][j] = dp[i-1][j-1] + 1。
2.如果X[i] != Y[j],则dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
为了只使用2*min(m, n)个表项,我们可以只存储min(m, n)行和min(m, n)列的数据,因为其他的数据可以通过填充规则从这些数据推导出来。
现在,我们使用Go语言来实现这个算法:
package main
import ("fmt"
)
func LCSLength(X string, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, Xm, n = n, m}minLen := min(m, n)// 初始化dp数组dp := make([][]int, minLen+1)for i := range dp {dp[i] = make([]int, minLen+1)}// 填充dp数组for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if X[i-1] == Y[j-1] {dp[i][j] = dp[i-1][j-1] + 1} else {dp[i][j] = max(dp[i-1][j], dp[i][j-1])}}}return dp[m][n]
}
func min(a, b int) int {if a < b {return a}return b
}
func max(a, b int) int {if a > b {return a}return b
}
func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println("The length of LCS is:", LCSLength(X, Y))
}
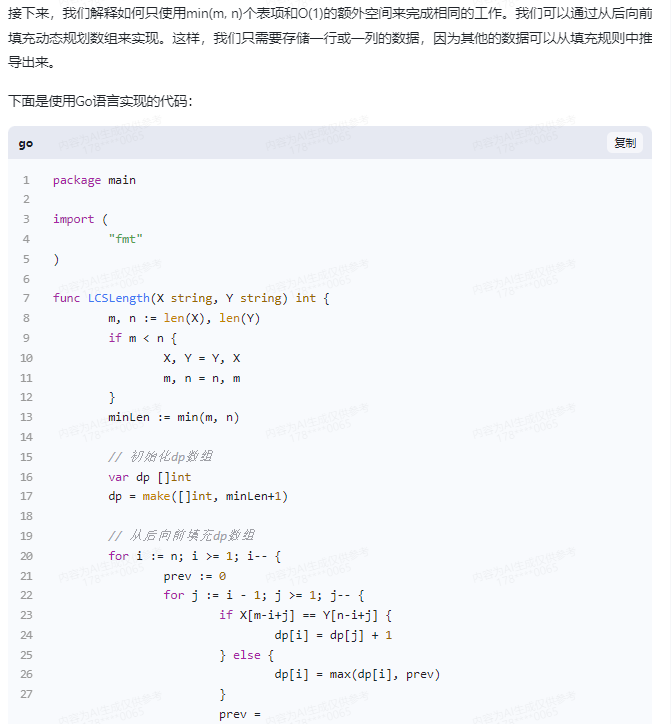
接下来,我们解释如何只使用min(m, n)个表项和O(1)的额外空间来完成相同的工作。我们可以通过从后向前填充动态规划数组来实现。这样,我们只需要存储一行或一列的数据,因为其他的数据可以从填充规则中推导出来。
下面是使用Go语言实现的代码:
package main
import ("fmt"
)
func LCSLength(X string, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, Xm, n = n, m}minLen := min(m, n)// 初始化dp数组var dp []intdp = make([]int, minLen+1)// 从后向前填充dp数组for i := n; i >= 1; i-- {prev := 0for j := i - 1; j >= 1; j-- {if X[m-i+j] == Y[n-i+j] {dp[i] = dp[j] + 1} else {dp[i] = max(dp[i], prev)}prev =

天工:
To compute the length of the Longest Common Subsequence (LCS) using only 2*min(m, n) space plus O(1) additional space, you can use a technique called space optimization in the DP approach. Here’s a Go implementation that demonstrates how to achieve this by only filling in necessary cells in the DP table:
package mainimport "fmt"// lcsLength computes the length of the LCS using space optimization.
func lcsLength(X, Y string) int {m, n := len(X), len(Y)// Determine the maximum size needed for the DP table.maxSize := m + ndp := make([]int, maxSize) // Dynamic programming array.var idx int // Index into the dynamic programming array.var lcsLength func(xIdx, yIdx int) intlcsLength = func(xIdx, yIdx int) int {if xIdx == 0 || yIdx == 0 {return 0}if dp[idx] > 0 {return dp[idx]-1}len1 := lcsLength(xIdx-1, yIdx)len2 := lcsLength(xIdx, yIdx-1)if X[xIdx-1] == Y[yIdx-1] {len3 := lcsLength(xIdx-1, yIdx-1)dp[idx] = 3return max(len1, max(len2, len3))} else {dp[idx] = 2return max(len1, len2)}}// Traverse the strings in the order that minimizes the space complexity.// This is achieved by starting with the longer string and then the shorter one.if m > n {for i := 1; i <= n; i++ {lcsLength(m, i)idx++}} else {for i := 1; i <= m; i++ {lcsLength(i, n)idx++}}return dp[idx]
}// max returns the larger of two integers.
func max(a, b int) int {if a >= b {return a}return b
}func main() {X := "AGGTAB"Y := "GXTXAYB"length := lcsLength(X, Y)fmt.Printf("Length of LCS: %d\n", length)
}
This implementation avoids filling the entire DP table by only working on the cells that contribute to the LCS length. The lcsLength function is the recursive part that calculates the length at each position, updating the dp array and the current index idx.
To reduce the space usage further, to just min(m, n) space plus O(1) additional space, you can use a stack or a queue to keep track of the indices instead of the dp array. However, this approach would require a more complex recursive function that maintains the stack or queue, which could make the code less clear.
The above code is optimized for space complexity, but due to its recursive nature, it may use more stack space than an iterative version. An iterative implementation with a stack could be used to ensure that the space complexity is truly O(1), but it would be more complex and likely not provide any significant performance improvements unless you are dealing with extremely large strings.



灵小智:
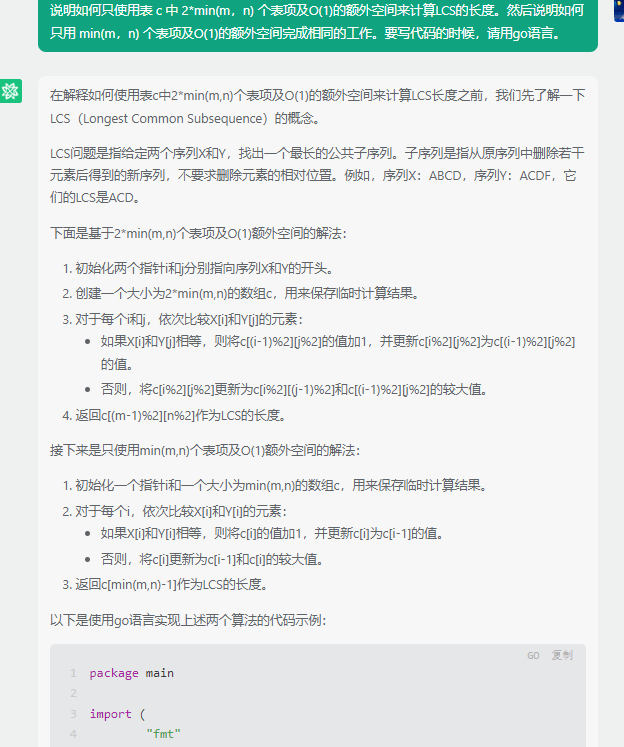
在解释如何使用表c中2*min(m,n)个表项及O(1)的额外空间来计算LCS长度之前,我们先了解一下LCS(Longest Common Subsequence)的概念。
LCS问题是指给定两个序列X和Y,找出一个最长的公共子序列。子序列是指从原序列中删除若干元素后得到的新序列,不要求删除元素的相对位置。例如,序列X:ABCD,序列Y:ACDF,它们的LCS是ACD。
下面是基于2*min(m,n)个表项及O(1)额外空间的解法:
- 初始化两个指针i和j分别指向序列X和Y的开头。
- 创建一个大小为2*min(m,n)的数组c,用来保存临时计算结果。
- 对于每个i和j,依次比较X[i]和Y[j]的元素:
- 如果X[i]和Y[j]相等,则将c[(i-1)%2][j%2]的值加1,并更新c[i%2][j%2]为c[(i-1)%2][j%2]的值。
- 否则,将c[i%2][j%2]更新为c[i%2][(j-1)%2]和c[(i-1)%2][j%2]的较大值。
- 返回c[(m-1)%2][n%2]作为LCS的长度。
接下来是只使用min(m,n)个表项及O(1)额外空间的解法:
- 初始化一个指针i和一个大小为min(m,n)的数组c,用来保存临时计算结果。
- 对于每个i,依次比较X[i]和Y[i]的元素:
- 如果X[i]和Y[i]相等,则将c[i]的值加1,并更新c[i]为c[i-1]的值。
- 否则,将c[i]更新为c[i-1]和c[i]的较大值。
- 返回c[min(m,n)-1]作为LCS的长度。
以下是使用go语言实现上述两个算法的代码示例:
package mainimport ("fmt"
)func LCSLengthUsing2Tables(X, Y string, m, n int) int {c := make([][]int, 2)for i := 0; i < 2; i++ {c[i] = make([]int, n+1)}for i := 0; i <= m; i++ {for j := 0; j <= n; j++ {if i == 0 || j == 0 {c[i%2][j%2] = 0} else if X[i-1] == Y[j-1] {c[i%2][j%2] = c[(i-1)%2][j%2] + 1} else {c[i%2][j%2] = max(c[i%2][(j-1)%2], c[(i-1)%2][j%2])}}}return c[m%2][n%2]
}func LCSLengthUsing1Table(X, Y string, m, n int) int {c := make([]int, n+1)for i := 1; i <= m; i++ {prev := 0for j := 1; j <= n; j++ {temp := c[j]if X[i-1] == Y[j-1] {c[j] = prev + 1} else {c[j] = max(c[j-1], c[j])}prev = temp}}return c[n]
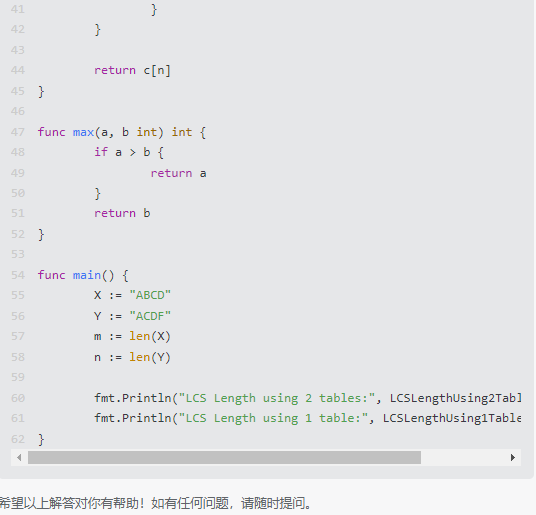
}func max(a, b int) int {if a > b {return a}return b
}func main() {X := "ABCD"Y := "ACDF"m := len(X)n := len(Y)fmt.Println("LCS Length using 2 tables:", LCSLengthUsing2Tables(X, Y, m, n))fmt.Println("LCS Length using 1 table:", LCSLengthUsing1Table(X, Y, m, n))
}
希望以上解答对你有帮助!如有任何问题,请随时提问。

chatgpt:
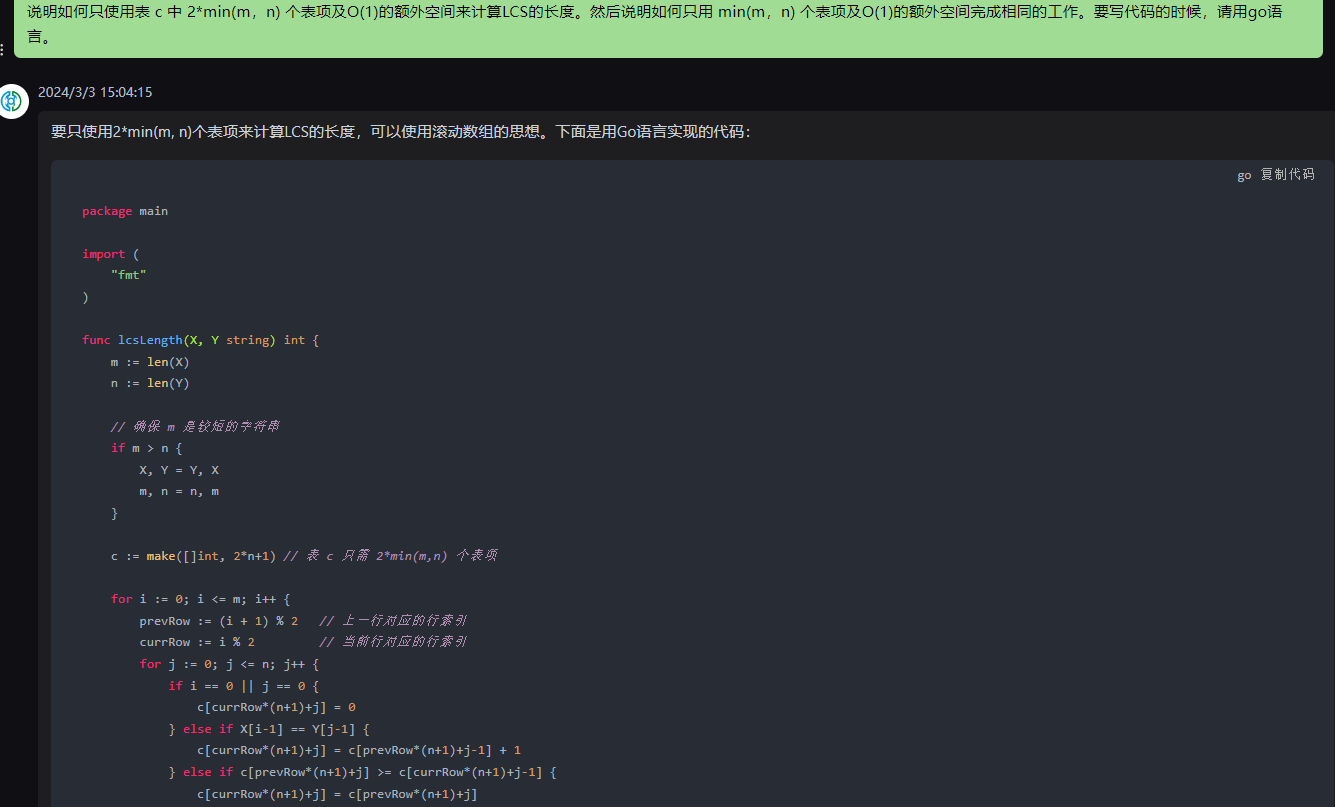
要只使用2*min(m, n)个表项来计算LCS的长度,可以使用滚动数组的思想。下面是用Go语言实现的代码:
package mainimport ("fmt"
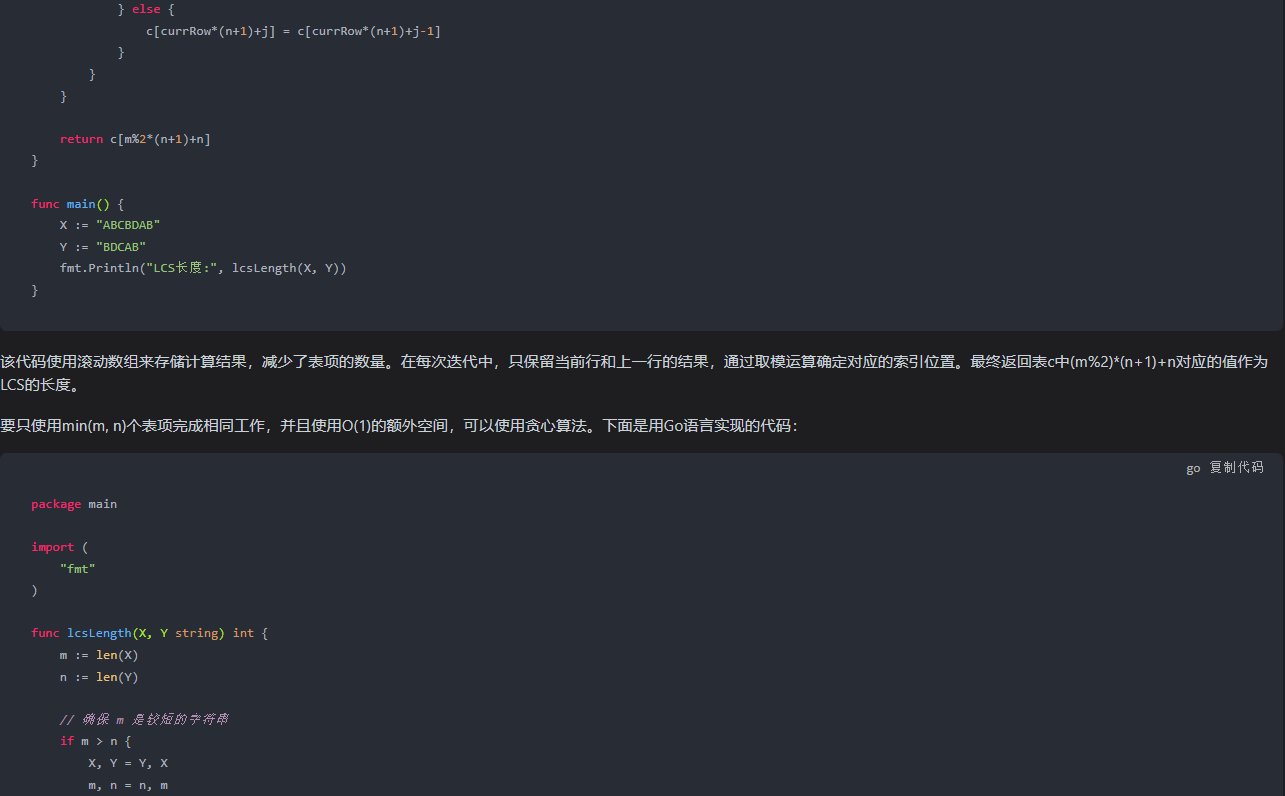
)func lcsLength(X, Y string) int {m := len(X)n := len(Y)// 确保 m 是较短的字符串if m > n {X, Y = Y, Xm, n = n, m}c := make([]int, 2*n+1) // 表 c 只需 2*min(m,n) 个表项for i := 0; i <= m; i++ {prevRow := (i + 1) % 2 // 上一行对应的行索引currRow := i % 2 // 当前行对应的行索引for j := 0; j <= n; j++ {if i == 0 || j == 0 {c[currRow*(n+1)+j] = 0} else if X[i-1] == Y[j-1] {c[currRow*(n+1)+j] = c[prevRow*(n+1)+j-1] + 1} else if c[prevRow*(n+1)+j] >= c[currRow*(n+1)+j-1] {c[currRow*(n+1)+j] = c[prevRow*(n+1)+j]} else {c[currRow*(n+1)+j] = c[currRow*(n+1)+j-1]}}}return c[m%2*(n+1)+n]
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println("LCS长度:", lcsLength(X, Y))
}
该代码使用滚动数组来存储计算结果,减少了表项的数量。在每次迭代中,只保留当前行和上一行的结果,通过取模运算确定对应的索引位置。最终返回表c中(m%2)*(n+1)+n对应的值作为LCS的长度。
要只使用min(m, n)个表项完成相同工作,并且使用O(1)的额外空间,可以使用贪心算法。下面是用Go语言实现的代码:
package mainimport ("fmt"
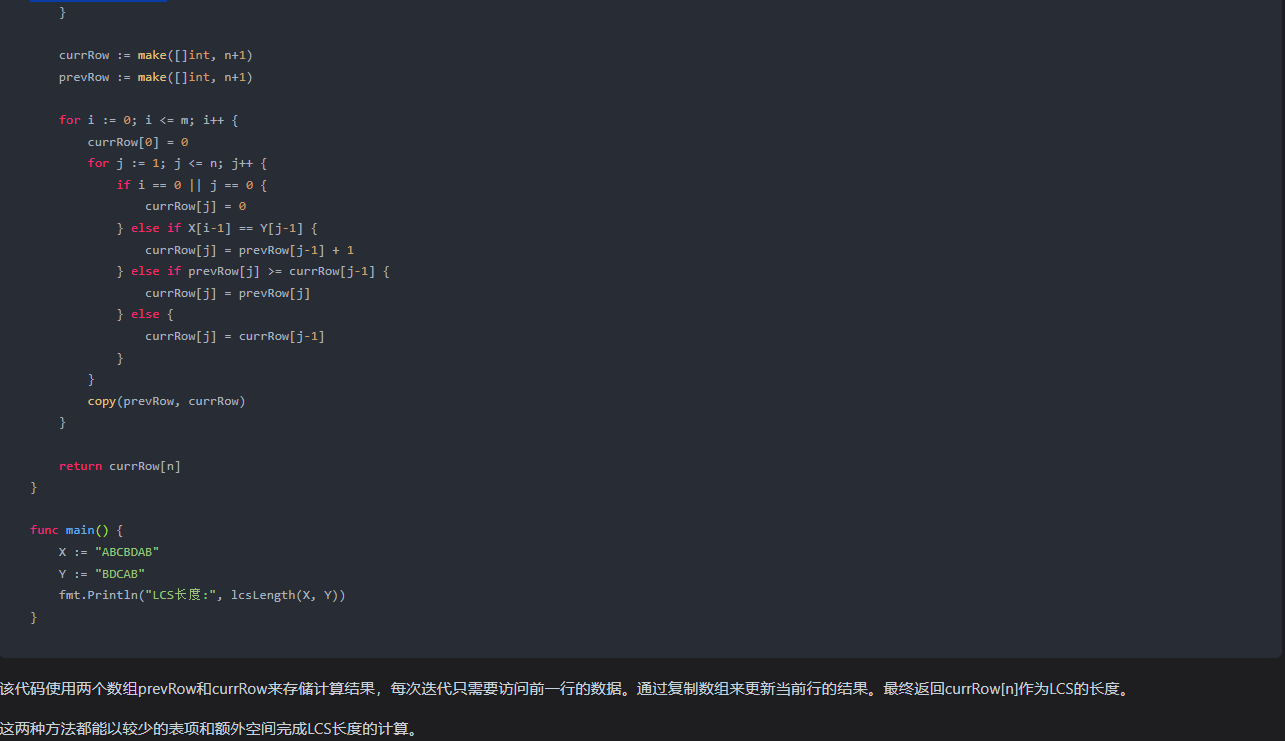
)func lcsLength(X, Y string) int {m := len(X)n := len(Y)// 确保 m 是较短的字符串if m > n {X, Y = Y, Xm, n = n, m}currRow := make([]int, n+1)prevRow := make([]int, n+1)for i := 0; i <= m; i++ {currRow[0] = 0for j := 1; j <= n; j++ {if i == 0 || j == 0 {currRow[j] = 0} else if X[i-1] == Y[j-1] {currRow[j] = prevRow[j-1] + 1} else if prevRow[j] >= currRow[j-1] {currRow[j] = prevRow[j]} else {currRow[j] = currRow[j-1]}}copy(prevRow, currRow)}return currRow[n]
}func main() {X := "ABCBDAB"Y := "BDCAB"fmt.Println("LCS长度:", lcsLength(X, Y))
}
该代码使用两个数组prevRow和currRow来存储计算结果,每次迭代只需要访问前一行的数据。通过复制数组来更新当前行的结果。最终返回currRow[n]作为LCS的长度。
这两种方法都能以较少的表项和额外空间完成LCS长度的计算。
kimi:
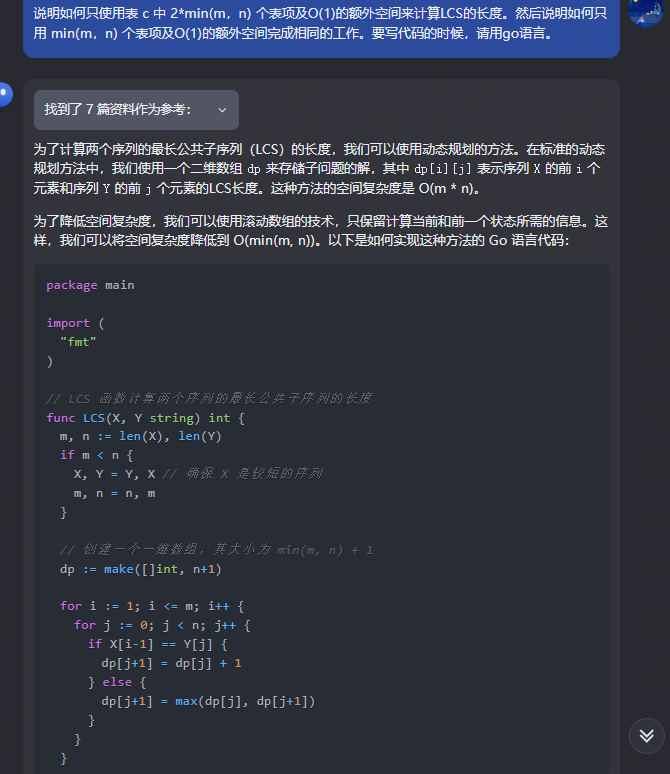
为了计算两个序列的最长公共子序列(LCS)的长度,我们可以使用动态规划的方法。在标准的动态规划方法中,我们使用一个二维数组 dp 来存储子问题的解,其中 dp[i][j] 表示序列 X 的前 i 个元素和序列 Y 的前 j 个元素的LCS长度。这种方法的空间复杂度是 O(m * n)。
为了降低空间复杂度,我们可以使用滚动数组的技术,只保留计算当前和前一个状态所需的信息。这样,我们可以将空间复杂度降低到 O(min(m, n))。以下是如何实现这种方法的 Go 语言代码:
package mainimport ("fmt"
)// LCS 函数计算两个序列的最长公共子序列的长度
func LCS(X, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, X // 确保 X 是较短的序列m, n = n, m}// 创建一个一维数组,其大小为 min(m, n) + 1dp := make([]int, n+1)for i := 1; i <= m; i++ {for j := 0; j < n; j++ {if X[i-1] == Y[j] {dp[j+1] = dp[j] + 1} else {dp[j+1] = max(dp[j], dp[j+1])}}}// 返回最长公共子序列的长度return dp[n]
}// max 返回两个整数中的最大值
func max(a, b int) int {if a > b {return a}return b
}func main() {X := "ABCBDAB"Y := "BDCABA"length := LCS(X, Y)fmt.Printf("Length of LCS: %d\n", length)
}
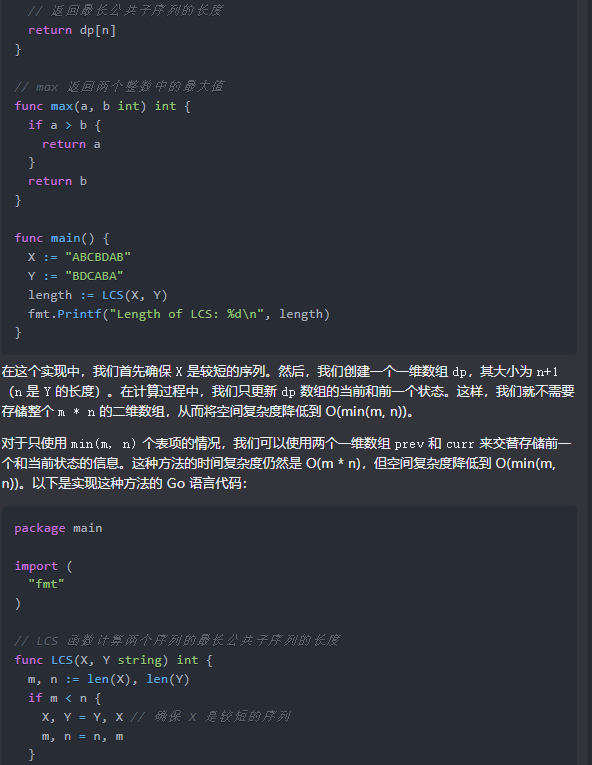
在这个实现中,我们首先确保 X 是较短的序列。然后,我们创建一个一维数组 dp,其大小为 n+1(n 是 Y 的长度)。在计算过程中,我们只更新 dp 数组的当前和前一个状态。这样,我们就不需要存储整个 m * n 的二维数组,从而将空间复杂度降低到 O(min(m, n))。
对于只使用 min(m, n) 个表项的情况,我们可以使用两个一维数组 prev 和 curr 来交替存储前一个和当前状态的信息。这种方法的时间复杂度仍然是 O(m * n),但空间复杂度降低到 O(min(m, n))。以下是实现这种方法的 Go 语言代码:
package mainimport ("fmt"
)// LCS 函数计算两个序列的最长公共子序列的长度
func LCS(X, Y string) int {m, n := len(X), len(Y)if m < n {X, Y = Y, X // 确保 X 是较短的序列m, n = n, m}// 创建两个一维数组,每个大小为 n+1prev := make([]int, n+1)curr := make([]int, n+1)for i := 1; i <= m; i++ {for j := 0; j < n; j++ {if X[i-1] == Y[j] {curr[j+1] = prev[j] + 1} else {curr[j+1] = max(prev[j], curr[j])}}// 交换 prev 和 currprev, curr = curr, prev}// 返回最长公共子序列的长度return prev[n]
}// max 返回两个整数中的最大值
func max(a, b int) int {if a > b {return a}return b
}func main() {X := "ABCBDAB"Y := "BDCABA"length := LCS(X, Y)fmt.Printf("Length of LCS: %d\n", length)
}
在这个实现中,我们使用两个一维数组 prev 和 curr 来交替存储前一个和当前状态的信息。在每次迭代时,我们更新 curr 数组,并在迭代结束后交换 prev 和 curr 的角色。这样,我们只需要 min(m, n) 个表项来完成计算。
混元:
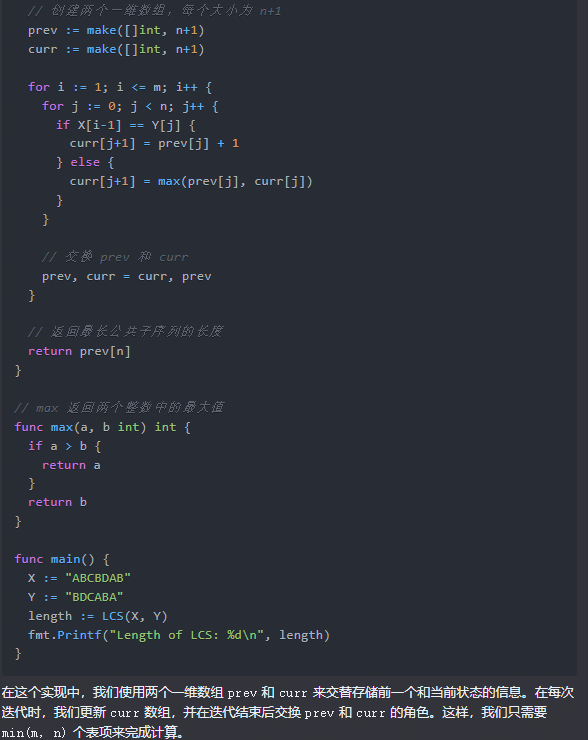
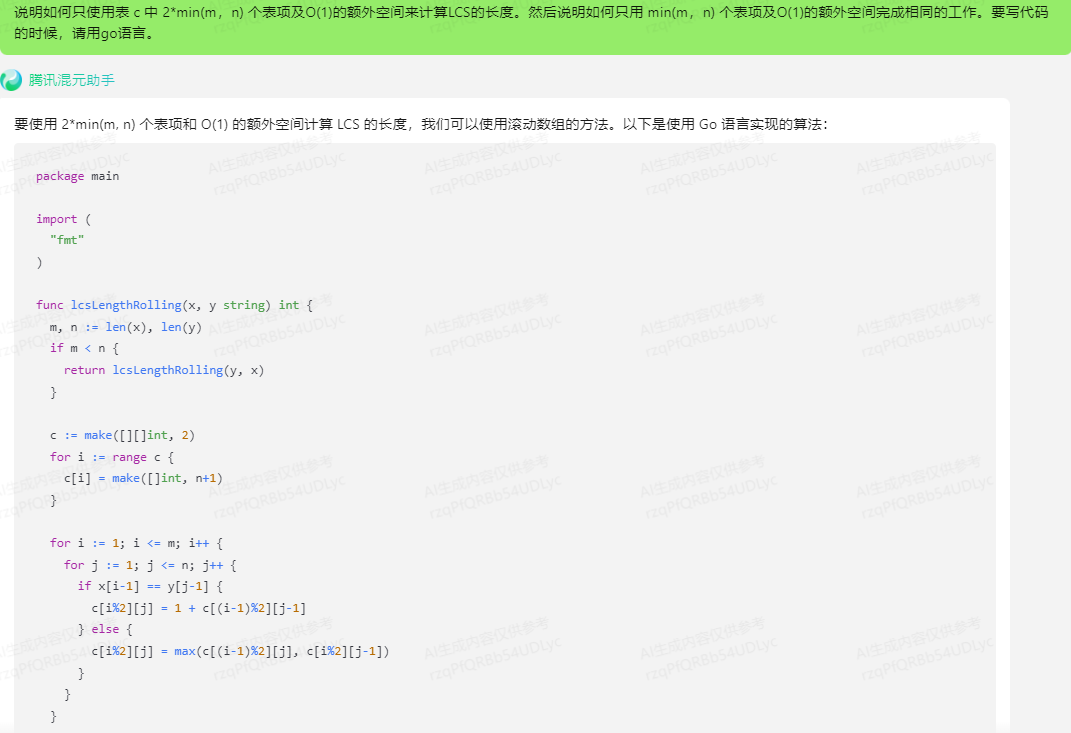
要使用 2*min(m, n) 个表项和 O(1) 的额外空间计算 LCS 的长度,我们可以使用滚动数组的方法。以下是使用 Go 语言实现的算法:
package mainimport ("fmt"
)func lcsLengthRolling(x, y string) int {m, n := len(x), len(y)if m < n {return lcsLengthRolling(y, x)}c := make([][]int, 2)for i := range c {c[i] = make([]int, n+1)}for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if x[i-1] == y[j-1] {c[i%2][j] = 1 + c[(i-1)%2][j-1]} else {c[i%2][j] = max(c[(i-1)%2][j], c[i%2][j-1])}}}return c[m%2][n]
}func max(a, b int) int {if a > b {return a}return b
}func main() {x := "ABCBDAB"y := "BDCAB"fmt.Printf("The length of the LCS is: %d\n", lcsLengthRolling(x, y))
}
要使用 min(m, n) 个表项和 O(1) 的额外空间计算 LCS 的长度,我们可以使用一个一维数组,并在计算过程中覆盖旧的值。以下是使用 Go 语言实现的算法:
package mainimport ("fmt"
)func lcsLengthMin(x, y string) int {m, n := len(x), len(y)if m < n {return lcsLengthMin(y, x)}c := make([]int, n+1)for i := 1; i <= m; i++ {prev := 0for j := 1; j <= n; j++ {temp := c[j]if x[i-1] == y[j-1] {c[j] = 1 + prev} else {c[j] = max(c[j], c[j-1])}prev = temp}}return c[n]
}func max(a, b int) int {if a > b {return a}return b
}func main() {x := "ABCBDAB"y := "BDCAB"fmt.Printf("The length of the LCS is: %d\n", lcsLengthMin(x, y))
}
这两个实现都可以在 O(mn) 的时间复杂度内计算 LCS 的长度,但使用的空间复杂度分别为 O(min(m, n)) 和 O(2*min(m, n))。


相关文章:

文心一言 VS 讯飞星火 VS chatgpt (207)-- 算法导论15.4 4题
四、说明如何只使用表 c 中 2*min(m,n) 个表项及O(1)的额外空间来计算LCS的长度。然后说明如何只用 min(m,n) 个表项及O(1)的额外空间完成相同的工作。要写代码的时候,请用go语言。 文心一言: 在只使用 2 * min(m, n) 个表项和 …...

【论文笔记】Attention Is All You Need
【论文笔记】Attention Is All You Need 文章目录 【论文笔记】Attention Is All You NeedAbstract1 Introduction2 Background补充知识:软注意力 soft attention 和硬注意力 hard attention?补充知识:加法注意力机制和点乘注意力机制Extende…...
(亲测可用)Adobe Photoshop 2024下载与安装
背景介绍:Adobe Photoshop 2024 是全球最受欢迎的图像编辑软件之一,2024年的版本带来了一系列令人印象深刻的功能: AI增强的自动选择和蒙版工具:现在,用户可以更轻松地选择和处理复杂的图像元素。更多的3D渲染功能&…...

uniapp聊天记录本地存储(详细易懂)
目录 目录 1、通过websocket拿取数据 2、获取聊天数据 3、聊天信息存储 、更新 4、读取聊天记录 5、发送信息,信息获取 6、最终效果 1.聊天信息的存储格式 2、样式效果 写聊天项目,使用到了本地存储。需要把聊天信息保存在本地,实时获…...

Vue.js中的$nextTick
其实目前在我现有的开发经历中,我还没有实际运用过$nextTick,今天在看书时,学习到了这个东西,所以做个笔记记录一下。 一、$nextTick是什么? $nextTick 是 Vue提供的一个方法,用于在 DOM 更新之后执行回调…...
python+mysql咖啡店推荐系统django+vue
(1).研究的基本内容 系统的角色分为: 1.管理员 2.会员 3.非会员 角色不同,权限也不相同 技术栈 后端:python 前端:vue.jselementui 框架:django/flask Python版本:python3.7 数据库:mysql5.7…...
综合实验nginx+nfs+kpa
综合实验 实验目的: 静态资源和动态资源分别存放在远端存储NFS上,NFS上数据实现实时备份,用户通过负载访问后端的web服务。实现ngixn负载高可用,当keepalived master宕机,vip能自动跳转到备用节点 实验环境ÿ…...
springboot197基于springboot的毕业设计系统的开发
简介 【毕设源码推荐 javaweb 项目】基于springbootvue 的毕业设计系统的开发 适用于计算机类毕业设计,课程设计参考与学习用途。仅供学习参考, 不得用于商业或者非法用途,否则,一切后果请用户自负。 看运行截图看 第五章 第四章 …...

group by报错
# 报错:[42000][1055] Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column base.biz_org_rep.ID which is not functionally dependent on columns in GROUP BY clause; this is incompatible with sql_modeonly_full_grou…...

3、云原生安全之falco的部署
文章目录 1、helm安装2、拉去镜像失败与解决3、安装faclo4、安装nfs服务器,配置k8s的持久卷4.1、创建nfs服务器,4.2、部署master节点(nsf服务的客户端)4.3、pv与pvc4.4、假设pv和pvc的配置文件出错了5、安装falcosidekick可视化(建议跳过,直接使用6)6、安装faclo与falco…...
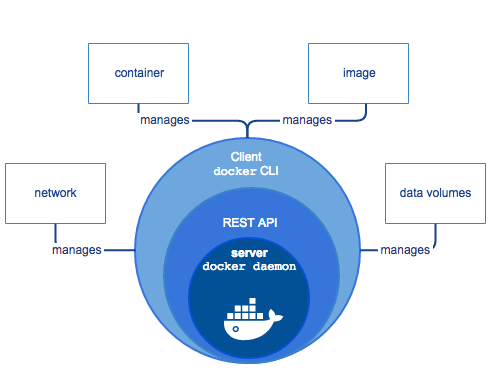
Docker架构概述
Docker是基于Go语言实现的开源容器项目,能够把开发的应用程序自动部署到容器的开源的应用容器引擎。Docker的构想是要实现"Build, Ship and Run Any App, Anywhere",即通过对应用的封装(Packaging)、分发(Distribution)、部署(Deployment)、运…...
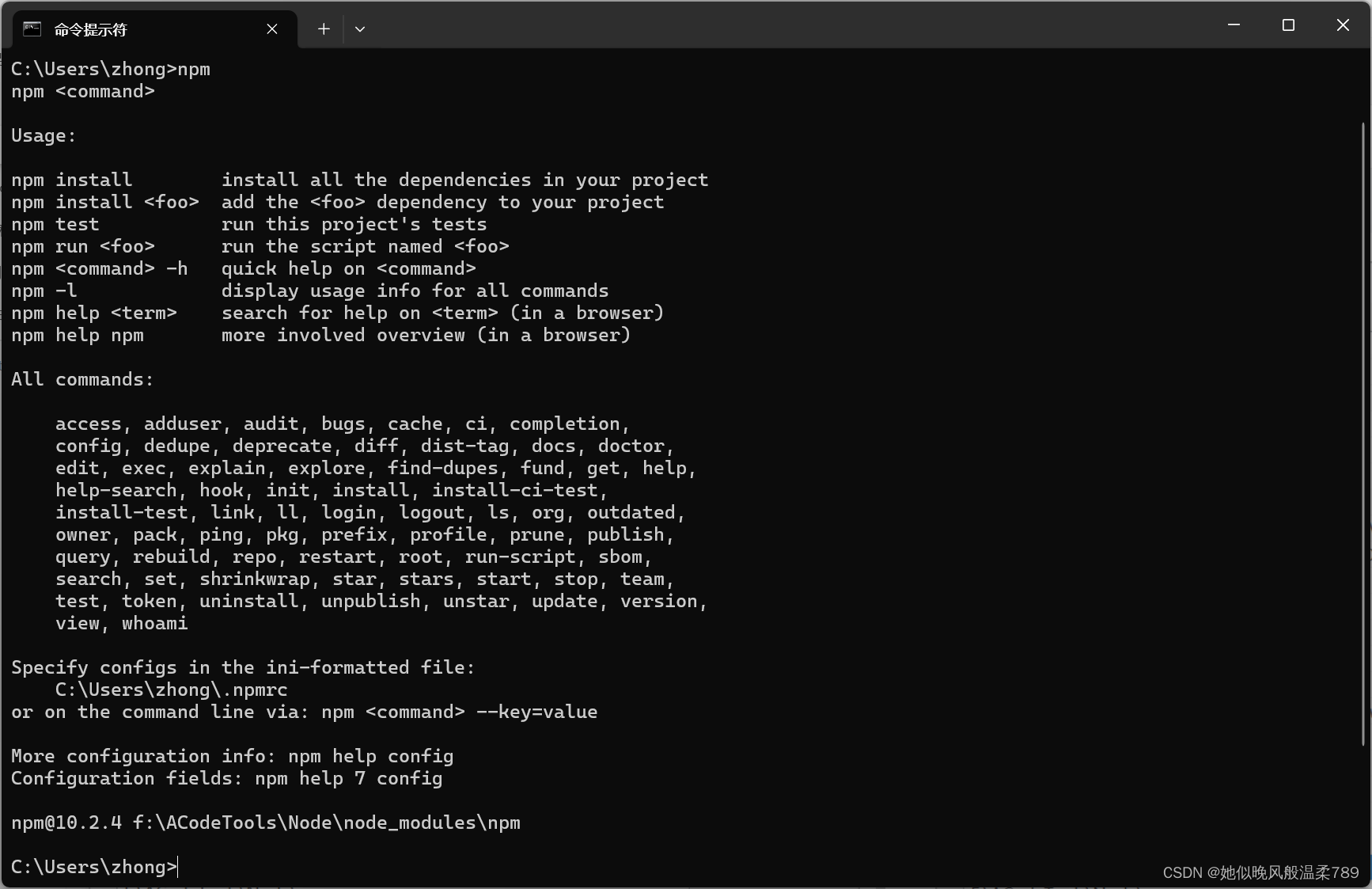
安装 node 错误的配置环境变量之后使用 npm 报错
安装 node 错误的配置环境变量之后使用 npm 报错 node:internal/modules/cjs/loader:1147 throw err; ^ Error: Cannot find module ‘F:\ACodeTools\Node\node_modules\npm\bin\node_modules\npm\bin\npm-cli.js’ at Module._resolveFilename (node:internal/modules/cjs/loa…...

Matlab 最小二乘插值(曲线拟合)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 在多项式插值时,当数据点个数较多时,插值会导致多项式曲线阶数过高,带来不稳定因素。因此我们可以通过固定幂基函数的最高次数 m(m < n),来对我们要拟合的曲线进行降阶。之前的函数形式就可以变为: 二、实现…...

AWTK-MVVM 配置文件模型
配置文件模型 AWTK-MVVM 内置了一些配置文件模型,用于读写各种配置文件,比如,JSON/XML/INI/CSV/UBJSON 等。 文件名中可以引用下面的变量。 ${app_dir} 应用程序目录${user_dir} 用户目录${temp_dir} 临时目录 json(url${app_dir}/demos/de…...

【活动】金三银四,前端工程师如何把握求职黄金期
随着春意盎然的气息弥漫大地,程序员群体中也迎来了一年一度的“金三银四”求职热潮。这个时间段对于广大前端工程师而言,不仅象征着生机勃发的新起点,更是他们职业生涯中至关重要的转折点。众多知名公司在这一时期大规模开启招聘通道…...
萌新学习RSA第二天(离线分解整数N)
1.yafu的使用(离线环境分解N)、 下载 打开 及使用 下载地址:https://sourceforge.net/projects/yafu/ 在下载好的并解压好的文件夹上鼠标右键打开终端 然后输入.\yafu-x64.exe并回车运行 .\yafu-x64.exe 来到这个页面就OK了 然后输入 fa…...
STM32学习和实践笔记(1): 装好了的keil μVision 5
2019年3月在淘宝上买了这块STM32的开发板,学了一段时间后就丢下了,今天重新捡起来,决定好好学习、天天向上。 对照教程,今天先把keil5装上了。 装的过程有以下几点值得记录下: 1)用注册机时,…...

企业计算机服务器中了360勒索病毒如何解密,360后缀勒索病毒处理流程
对于众多的企业来说,企业的数据是企业发展的核心,越来越多的企业开始注重企业的数据安全问题,但随着网络技术的不断发展与应用,网络黑客的攻击加密手段也在不断升级。近期,云天数据恢复中心接到多家企业的求助…...

【图像拼接/视频拼接】论文精读:Efficient Video Stitching Based on Fast Structure Deformation
第一次来请先看这篇文章:【图像拼接(Image Stitching)】关于【图像拼接论文精读】专栏的相关说明,包含专栏使用说明、创新思路分享等(不定期更新) 图像拼接系列相关论文精读 Seam Carving for Content-Aware Image ResizingAs-Rigid-As-Possible Shape ManipulationAdap…...

LASSO算法
LASSO (Least Absolute Shrinkage and Selection Operator) 是一种回归分析的方法,它能够同时进行变量选择和正则化,以增强预测准确性和模型的解释性。LASSO通过在损失函数中加入一个L1惩罚项来实现这一点。该惩罚项对系数的绝对值进行约束。 基本概念 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...

[特殊字符] Spring Boot底层原理深度解析与高级面试题精析
一、Spring Boot底层原理详解 Spring Boot的核心设计哲学是约定优于配置和自动装配,通过简化传统Spring应用的初始化和配置流程,显著提升开发效率。其底层原理可拆解为以下核心机制: 自动装配(Auto-Configuration) 核…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...

Linux信号保存与处理机制详解
Linux信号的保存与处理涉及多个关键机制,以下是详细的总结: 1. 信号的保存 进程描述符(task_struct):每个进程的PCB中包含信号相关信息。 pending信号集:记录已到达但未处理的信号(未决信号&a…...
